Scambio termico per irraggiamento

Dalle teorie fisiche sappiamo che ogni corpo, semplicemente per il fatto di trovarsi ad una certa temperatura T emette nello spazio onde elettromagnetiche.

La trasmissione d’energia, sotto forma di calore, prende il nome d’irraggiamento termico. Tale fenomeno non è dissimile da ciò che accade nella propagazione di onde acustiche ma a differenza di queste ultime le onde elettromagnetiche, responsabili dell’irraggiamento termico, non necessitano di alcun mezzo per la propagazione.

Caratteristica fondamentale dell’irraggiamento risulta quindi essere la totale indipendenza da un particolare ambiente che puo’ comunque influenzare lo stato dei corpi. E’ quindi sufficiente che due corpi sì trovino a debita distanza perché possano assorbire l’uno l’irraggiamento del altro.

Essendo la potenza termica irraggiata da un corpo proporzionale alla temperatura e, data la natura dualistica dell’irraggiamento, cioè la possibilità da parte di un corpo di assorbire ed emettere contemporaneamente onde elettromagnetiche, si conclude che lo scambio termico per irraggiamento dipende dalla differenza di temperatura tra corpo e ambiente. L’equilibrio termico, quindi altro non è che la condizione per cui la quantità di energia emessa da un corpo è pari a quella ricevuta, di modo che la sua temperatura si mantenga costante.

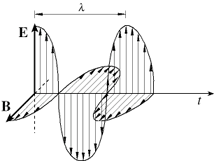
Di seguito è riportata la schematizzazione di un’onda elettromagnetica non polarizzata. Come si puo’ notare questa è un fenomeno generatosi dalla sovrapposizione degli effetti di due campi, il campo elettrico E e il campo magnetico B.

Si può parlare di onde elettromagnetiche e di propagazione d’energia solo quando il campo elettrico E, e il campo magnetico B, oscillano entrambi lungo il proprio asse in funzione del tempo, secondo le leggi stabilite dalle equazioni di Maxwell. Inoltre l’energia trasportata da un’onda (e quindi lo scambio energetico) è massima quando E e B oscillano in fase.

La propagazione dell’onda elettromagnetica avviene in direzione ortogonale al piano contenente E e B (perpendicolari tra loro), con una velocità massima nel vuoto =300000km/s pari alla velocità della luce. Considerando differenti mezzi di propagazione avremo differenti velocità associate all’onda; il rapporto tra e v, velocità specifica del mezzo, è definito indice di rifrazione assoluto , ed è una caratteristica peculiare di quel materiale:

. ( 1 )

Nella tabella 1 sono riportati gli indici di rifrazione assoluta per varie sostanze :

Aria	1,000294
H	1,000139
CO	1,000449
CH	1,482
Acqua	1,33
Alcool etilico	1,36
Cloruro di sodio	1,52

Tabella 1

Per il calcolo sperimentale sulla terra vengono normalmente trascurati gli effetti di transitorio data l’alta velocità di propagazione delle onde e dei fenomeni ad esse associati.

L’intensità I di un’onda elettromagnetica di qualsiasi natura diminuisce nell’attraversamento di un mezzo secondo la legge , dove è l’intensità nel vuoto e β è detto coefficiente d’estinzione. β ha le dimensioni dell’inverso di una lunghezza e rappresenta lo spessore che la radiazione deve attraversare perché la sua intensità si riduca di un fattore 1/e. Questa riduzione di intensità si traduce in una cessione, da parte dell’onda, di una parte dell’energia trasportata al mezzo in cui si sta propagando.

Il solo modello ondulatorio delle onde non è però sufficiente a dar ragione di alcuni comportamenti a livello microscopico. In questo ambito si richiede l’utilizzo della teoria quantistica delle onde elettromagnetiche che, pur coincidendo nell’ambito macroscopico con i fenomeni ondulatori, si è resa necessaria per la comprensione di alcuni aspetti altrimenti contradditori.

Secondo la fisica quantistica un atomo, quando un elettrone passa da uno stato quantico permesso d’energia ad uno inferiore d’energia , emette una quantità di energia uguale a -sotto forma d’onda elettromagnetica di frequenza f data da:

, ( 2 )

dove J/s é detta costante di Planck.

Avremo quindi che associata ad ogni molecola di un corpo vi sarà una corrispondente onda elettromagnetica; essendo ogni materiale formato da particolari combinazioni di sostanze, è stato possibile organizzare e ricoscere diversi composti semplicemente osservando il loro spettro.

Risulta quindi conveniente rappresentare lo spettro di emissione o di assorbimento secondo non la frequenza f, ma in funzione di una differente grandezza fisica λ detta lunghezza d’onda e ottenuta da:

. ( 3 )

Le varie lunghezze d’onda che compongono lo spettro di emissione di un corpo dipendono dalla natura del corpo stesso, mentre l’intensità dell’energia alle varie lunghezze d’onda è in relazione a come le molecole vengono eccitate. Un solido caldo, ad esempio, emette tutte le lunghezze d’onda, formando uno spettro continuo il quale, a seconda della temperatura, può andare da un rosso debolmente visibile ad un bianco brillante. Una radiazione è invece detta monocromatica se porta energia solo ad una frequenza.

Di seguito sono riportati gli spettri di assorbimento ed emissione di un atomo di sodio:

Coerentemente con la lunghezza d’onda associata un’onda viene classificata in diverse categorie. La tabella 2 riporta da sinistra a destra valori di λ sempre più grandi e, conseguentemente, f sempre più piccole.

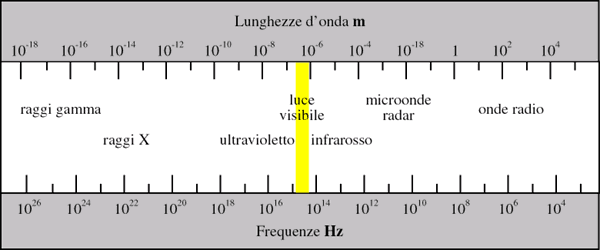
Tabella 2

Come si puo’ notare dalla tabella 2, le frequenze percepibili dall’occhio umano come luce visibile rappresentano solo una piccola parte delle onde elettromagnetiche conosciute, con lunghezza d’onda l compresa tra i 400 e i 700 nanometri. Di seguito vengono riportate brevi descrizioni delle onde che compaiono in tabella:

1) Onde Hertziane: l 10⁹-10⁶ m f 50-1000 Hz

Responsabili dell’inquinamento elettromagnetico causato dalle linee elettriche dell’alta tensione; possibili effetti negativi derivano dalla grande energia associata al campo elettrico e magnetico.

2) Onde radio: l fino a 10^-2 m f fino a 2 GHz

Enorme utilizzo nelle applicazioni di telecomunicazioni. Per particolari tipi di schede di rete vengono usate onde radio anche a 4 GHz.

3) Microonde: l fino a 10^-3 m f fino a 10¹¹ Hz

Si possomo ottenere da scariche fra due elettrodi ad alta tensione,da circuiti oscillanti, da radiazione termica di corpi caldi. Per le applicazioni in telefonia, nella radio, nella televisione, nei radar.

4) Infrarosso: l 10^-3-10^-6 m f 2 10¹¹-10¹⁴ Hz

Con lunghezze d’onda appena più lunghe della luce visibile, questa gamma di radiazioni è responsabile della maggior parte degli effetti termici percepiti dall’uomo.

5) Luce visibile: l 0.4-0.7 mm f fino a 3 10¹⁴ Hz

Campo in cui la radiazione solare produce la massima energia. La maggior parte degli organismi viventi percepisce questo spettro come luce ambiente.

6) Ultravioletto: l 0.7 mm-10^-9 m f 10¹⁵-10^-17 Hz

Si raggiunge la soglia di pericolosità biologica in quanto queste onde,ancora poco penetranti, viaggiano su frequenze prossime a quelle di oscillazione degli elettroni nelle molecole. Possono quindi spezzare i legami chimici formati dagli atomi negli organismi viventi (es. proteine). Da queste frequenze in poi perdono d’importanza gli effetti termici relativi al trasferimento del calore.

7) Raggi X: l 10^-10-10^-11 m f 10¹⁷-10¹⁹ Hz

Applicazioni nella medicina e nella metallurgia, al pari degli ultravioletti i raggi X possono avere effetti dannosi sugli organismi viventi.

8) Raggi g: l < 10^-11 m f > 10¹⁹ Hz

Onde ad altissima frequenza, sono proprie della radiazione cosmica di fondo,sono comunque ben schermate dall’atmosfera terrestre.

L’ultravioletto,i raggi X e g, sono dette radiazioni ionizzanti, nome derivato dalla capacità da parte di queste onde di far entrare in risonza gli elettroni nelle molecole e quindi ionizzare l’atomo.

Dal punto di vista del trasferimento di calore, sono però interessanti la gamma di lunghezze d’onda comprese tra e , in cui l’irraggiamento è più consistente. Un telefono cellulare dual band, ad esempio, che trasmette a 1800 MHz (λ=0,16m) essendo vicino a questa zona dello spettro trasmette una quantità di energia apprezzabile, sotto forma di calore, all’orecchio dell’utente.

A questo punto è vantaggioso introdurre una nuova grandezza fisica chiamata potere emissivo integrale. Tale grandezza è definita come la quantità d’energia che viene irradiata dall’unità di superficie nell’unità di tempo, s’indica e si misura in W/m².

( 4 ).

Il valore di dipende dalla natura fisica del corpo e dalla sua temperatura. Il potere emissivo integrale è costituito dai tutti i contributi relativi agli intervalli di lunghezza d’onda che compongono lo spettro; facendo tendere a zero anche tende a zero. Il loro rapporto tende però ad un valore finito, detto potere emissivo monocromatico , definito dalla relazione:

. ( 5 ).

L’unita di misura di ε è W/.

Integrando l’equazione precedente, essendo funzione dello stato superficiale del corpo, della lunghezza d’onda λ e della temperatura T si ottiene che:

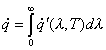. ( 6 )

Quando un fascio di energia, sotto forma di calore, incide contro un qualsiasi corpo, una parte dell’energia totale, che indicheremo con ,viene riflessa verso nella direzione di provenienza, una parte, ,viene assorbita dal corpo, ed infine una parte attraversa il corpo.

Riassumendo è quindi possibile scrivere:

=++, ( 7 )

dividendo ambo i membri per il potere emissivo otteniamo:

. ( 8 )

Se si definiscono i coeficienti a di assorbimento, r di riflessione, t di trasmissione, come i rapporti tra le corrispondenti porzioni di energia e il suo valore complessivo, dall’equazione precedente si ricava:

1=a+r+t. ( 9 )

Viene definito opaco un corpo che non viene attraversato da onde elettromagnetiche (per il quale si ha quindi t=0). Tale caratteristica è comune a quasi tutti i materiali solidi di spessore superiore allo strato superficiale per i quali l’ equazione ( 9 ) si riduce a:

a+r=1. ( 10 )

A temperatura ambiente il potere emissivo integrale di praticamente tutti i corpi in natura è trascurabile rispetto al flusso di energia irradiato dal sole. In conseguenza di ciò, abbiamo che il colore di un particolare oggetto non è determinato dalle frequenze emesse dal corpo stesso, bensì dalle componenti della luce solare riflesse piuttosto che assorbite. In altre parole se un corpo è di colore blu ciò è dovuto al fatto che riflette le lunghezze d’onda corrispondenti al blu ed assorbe tutte le altre.

Il corpo nero

Si definisce corpo nero un corpo con coefficiente d’assorbimento a=1 per qualsiasi lunghezza d’onda, o analogamente con coefficiente di riflessione r=0. Sono invece chiamati corpi grigi quei corpi che possiedono il medesimo a per tutte le frequenze, anche se questo non è il medesimo valore per tutti. Per i corpi colorati questo coefficiente è funzione della lunghezza d’onda e ne identifica appunto il colore.

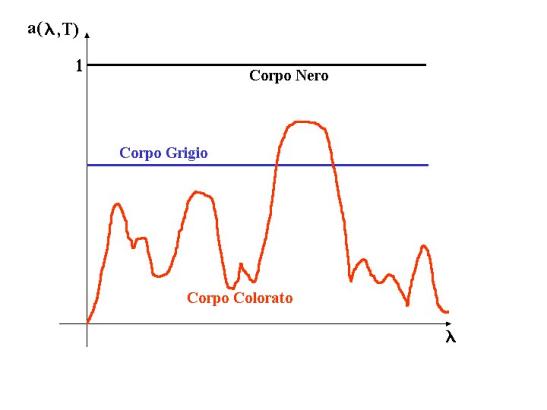
In termini energetici il corpo nero è un oggetto in grado di assorbire tutta l’energia incidente indipendentemente dalla lunghezza d’onda. Si ottiene praticamente considerando un corpo isotermo e cavo, la cui cavità (indipendentemente dalla forma) è di materiale con elevato coefficiente di assorbimento ed il più piccolo coefficiente di riflessione possibile, messo in contatto con l’esterno tramite un minuscolo foro.

Una volta che un raggio di luce entra nella cavità, colpendo la superficie interna, prima di uscire nuovamente deve essere riflesso un considerevole numero di volte; in pratica, cedendo una parte della sua energia al corpo ad ogni rilessione viene interamente assorbito.

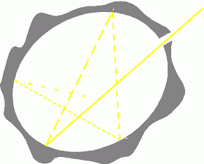
Se ora consideriamo una cavità di forma qualsiasi, con la superficie interna mantenuta a temperatura costante e vi introduciamo un corpo nero, avremo che questo, per unità di superficie, riceverà la potenza ed emetterà la potenza .

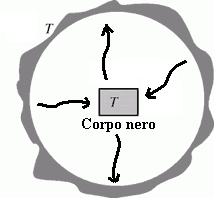
A regime, cioè una volta raggiunto l’equilibrio termico tra il corpo nero e la cavità, si avrà che:

=. ( 11 )

Data la definizione di corpo nero, la situazione definitiva è quella di un corpo che assorbe tanto calore quanto ne riceve a tutte le frequenze.

Se al posto del corpo nero mettiamo un corpo qualsiasi colorato, pur rimanendo uguale la potenza incidente , la potenza assorbita per unità di superficie dipende dal coefficiente di assorbimento a secondo la legge = e non è più la stessa a tutte le frequenze.

Definendo ora il coefficiente di emissitività e come il rapporto tra il potere emissivo integrale di un corpo qualsiasi e quello di un corpo nero ₀, ovvero:

, ( 12 )

possiamo affermare che la potenza specifica irradiata dal corpo nella cavità è data da , ma all’equilibrio deve essere=, quindi si ha che . Ora, sapendo che, possiamo riscrivere la ( 11 ) come:

a(l) = e(l) , ( 13 )

indipendentemente dalla natura del corpo e dalla sua temperatura.

Risulta quindi evidente che il corpo nero, oltre ad essere per definizione il corpo con il potere assorbente massimo, è anche quello con il coeficiente d’emissione maggiore; in quest’ambito diviene chiara l’affermazione per cui una stella rappresenta un perfetto esempio di corpo nero.

Nel considerare i corpi colorati, invece di corpi grigi o neri, le cose tendono a complicarsi notevolemente data la dipendenza delle caratteristiche intrinseche del corpo dalla lunghezza d’onda l ,oltre che dallo stato superficiale e dalla temperatura.

-

Se ci poniamo però in condizioni di equilibrio termico, l’energia ricevuta deve essere comunque uguale a quella emessa, anche per i corpi colorati, per cui la (13) rimane valida. Alla luce delle considerazioni fatte, visto che dal comportamento del corpo nero grazie a coefficienti correttivi, si riesce a risalire al comportamento di corpi qualsiasi, lo studio del corpo nero assume per l’irraggiamento la stessa importanza che hanno i gas perfetti in termodinamica oppure i fluidi perfetti in fluidodinamica.

Leggi del corpo nero

Legge di Stefan Boltzmann

Esiste una funzione che lega la grandezza fisica fondamentale del potere emissivo integrale del corpo nero alla sua temperatura, ed è nota come legge di Stefan-Boltzmann; la sua espressione è:

, ( 14 )

dove , ricavata dalla termodinamica quantistica, è detta costante di Stefan-Boltzmann.

Legge di Planck

Tale legge fornisce il legame che sussiste tra il potere emissivo monocromatico del corpo nero, la lunghezza d’onda l, e la temperatura T, ed è data da:

, ( 15 )

in cui compaiono:

(1^ costante di Planck)

(2^ costante di Planck)

Il seguente grafico mostra l’andamento diin funzione di l per alcuni valori di T espressi in gradi Kelvin:

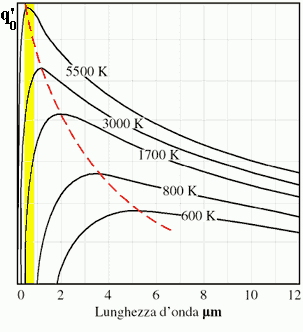
Alle basse temperature il massimo di si ha per valori di non percepiti dall’occhio umano, mentre un’aumento di T lo sposta verso le lunghezze d’onda di 0.4-0.7 mm, cioè proprio quelle della luce visibile . Questo spiega perché un corpo freddo è visibile solo se illuminato, mentre un corpo incandescente emana luce.

Grazie a questa dipendenza del potere emissivo monocromatico dalla temperatura, si è potuta definire una nuova grandezza fisica chiamata temperatura di colore. Tale parametro indica le temperature che competono ai particolari colori che formano lo spettro della luce visibile; così ad esempio al colore rosso vengono associate temperature basse, intorno ai 3500 K (lampade ad incandescenza), mentre al blu-violetto corrispondono temperature alte, tipicamente sui 7000 K (Xenon nei flash). Paradossalmente si è soliti, nella consuetudine, considerare “caldi” quei colori definiti da temperature di colore basse e “freddi” quei colori che si sviluppano ad alte temperature.

Esiste inoltre una normativa, risalente al 1975, che definisce, tra le altre cose, i parametri sulle sorgenti di luce nei vari ambienti: pubblici, lavorativi, scolastici, ecc. ecc. Alcuni di questi parametri, ad esempio, indicano che la quantità minima di luce da fornire in un’aula è di almeno 200 W/m², mentre la temperatura di colore considerata maggiormente stimolante è di 5500 K.

Legge di Wien

Strettamente legata alla legge di Planck, è la legge di Wien, che permette di calcolare la lunghezza d’onda alla quale corrisponde il massimo di . Derivando l’espressione della legge di Planck si ottiene:

_{, ( 16 )}

imponendo la condizione di annullamentoe semplificando l’espressione:

. ( 17 )

Risolvendo quest’equazione si ottiene la legge di Wien:

, ( 18 )

che fornisce appunto il luogo dei punti di massimo in funzione di T; come si può notare dal grafico precedente tale luogo è un ramo d’iperbole.

Legge di Prevost

La legge di Prevost definisce in maniera semplice l'energia che viene scambiata per irraggiamento:

(19).

Legge di Alambert

Vogliamo ora calcolare la quantità di energia irraggiata da una superficie in funzione dell’angolo solido visto da una determinata regione dello spazio. Conviene ricordare che si definisce angolo solido, il rapporto tra la superficie dS che un cono di apertura intercetta su di una sfera centrata sul vertice del cono ed il quadrato del raggio della sfera stessa, mentre la sua unità di misura è lo steradiante (Sr).

Se ora consideriamo un cono definente un’angolo solido d’ampiezza Dw e la quantità d’energia che ne attraversa la base, avremo che facendo tendere a zero l’ampiezza del cono, sia che Dw si annulleranno ma non il loro rapporto. Viene appunto definito potere emissivo angolare i il rapporto fra queste due grandezze:

( 20 )

e si misura in .

Per una sorgente puntiforme il valore di i sarà dato da:

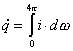, ( 21 )

mentre per un corpo esteso che irraggia su di un solo semispazio:

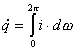. ( 22 )

Per lo studio dell’irraggiamento in genere si usano solo sorgenti estese.

Differente da i è l’intensità di radiazione I, definita come il rapporto tra la quantità d’energia fluente attraverso l’angolo solido d’ampiezza e l’angolo solido stesso, facendo sempre riferimento all’unità di tempo e di superficie valutata su di un piano normale all’asse dell’angolo solido. La differenza consiste semplicemente nel fatto che mentre il potere emissivo viene considerato sulla superficie che emette energia, l’intensità di radiazione è calcolata sulla superficie normale alla direzione scelta. Si può quindi definire un legame fra i ed I di natura prettamente geometrica :

, ( 23 )

dove è l’angolo tra la normale n della superficie del corpo e l’asse del cono.

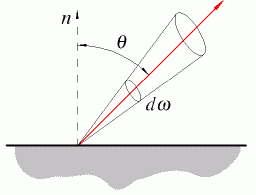
Per un corpo nero si ha che =costante, cioè l’intensità di radiazione è indipendentemente da J. Sostituendo in (23) si ottiene la cosiddetta legge di Lambert:

. ( 24 )

Se si considera più attentamente qusta legge si nota come la potenza emessa dal corpo nero non sia la stessa in ogni direzione, ma vari con l’angolo J. Indicando con il nome di solido fotometrico la figura geometrica che mostra come venga emessa la luce nello spazio, si capisce perchè il solido fotometrico di un corpo nero sia una sfera piuttosto che una semisfera.

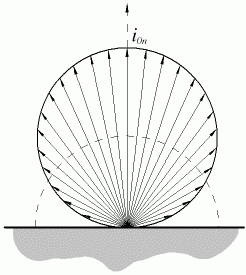
Un corpo grigio inoltre, viene detto lambertiano se mantiene lo stesso i di un corpo nero ovvero, se il suo solido fotometrico è ancora una sfera anche se di raggio minore. Per quanto riguarda i corpi colorati si ottengono generalmente solidi fotometrici di geometria complicata e di difficile espressione matematica.