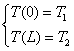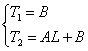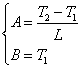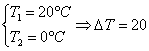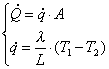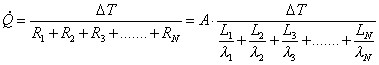|
Corso di Fisica Tecnica |
|
Anno 2001-2002 |
|
Prof.Angelo Farina |
|
Facoltà di Ingegneria – Università degli studi di
Parma |
Trasmissione del
calore
●
Equivalente termico della legge di Ohm
● Conduzione e relazioni fondamentali che lo regolano:
● Applicazioni degli argomenti trattati
Introduzione
Lo studio
dei fenomeni di trasmissione del calore riguarda tutti quei processi fisici nei
quali una certa quantità di energia termica è trasferita da un sistema ad un
altro a causa di una differenza di temperatura.
Tali
processi avvengono in accordo con i principi della termodinamica: quindi per il
primo principio, l’energia termica ceduta da un sistema deve essere uguale a
quella ricevuta dall’altro e il calore, come afferma il secondo principio,
passa dal corpo più caldo a quello più freddo. Tuttavia tra termodinamica e
trasmissione del calore c’è una fondamentale differenza. Infatti in ambito
termodinamico è irrilevante il tempo necessario affinché un dato processo sia ultimato, in quanto
ora, l’oggetto di studio della termodinamica sono i sistemi in equilibrio e le
grandezze fisiche in gioco sono considerate indipendenti dal tempo. Nella trasmissione del calore, chiamata
anche Termocinetica, ciò che conta è la rapidità in cui avviene il processo di
scambio termico. Riveste quindi notevole importanza la quantità di calore
scambiata nell’unità di tempo che prende il nome di potenza termica. Essa viene
indicata con il simbolo 
e poiché è una
potenza, nel sistema internazionale si misura in watt.
Riassumendo,
lo scopo della Termocinetica è studiare la velocità di scambio del calore
invece della quantità assoluta trasferita in un tempo infinito, come avviene in
Termodinamica.
Modalità di
scambio termico
La
trasmissione del calore avviene spontaneamente solo da un corpo caldo ad un
corpo freddo, fino a che i due corpi raggiungono la stessa temperatura, detta
di equilibrio termico. Il corpo caldo comunica a quello freddo parte della sua
energia termica intensificandone l’agitazione molecolare. La propagazione del
calore può avvenire per conduzione, convezione o per irraggiamento.
Conduzione
Il
trasferimento per conduzione avviene tra corpi che sono a contatto, o
tra parti di uno stesso corpo che si trovano a temperature diverse. Esso è
causato dal trasferimento di energia cinetica da una molecola a quella
adiacente che possiede una velocità di vibrazione minore. Poiché la velocità di
vibrazione delle particelle è direttamente proporzionale alla temperatura, il
corpo caldo cede energia a quello freddo, aumentandone la temperatura, finché
non è raggiunto l’equilibrio termico. Prendiamo ad esempio, come indicato in
figura 1a, due corpi a temperature diverse. Una volta posti in contatto, per
conduzione il calore fluisce dal corpo più caldo a quello più freddo, finché
essi raggiungono una temperatura d’equilibrio.
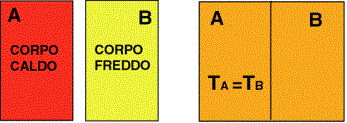
Fig.1a Fig.1b
Convezione
La
convezione ha luogo quando uno dei due corpi interessati dallo scambio
termico è un fluido, e la trasmissione del calore può essere associata ad un
trasferimento di materia. In un fluido a temperatura non uniforme, per effetto
combinato di un campo di temperatura e di velocità, si determina una
distribuzione dei valori di densità variabile da punto a punto, conseguenza dei
fenomeni di dilatazione termica. In questi casi le forze gravitazionali
provocano continui movimenti delle particelle del fluido, con conseguente
miscelazione, favorendo pertanto la trasmissione del calore dalle particelle
più calde a quelle più fredde. Questo fenomeno prende il nome di convezione
naturale. Quando invece i movimenti delle particelle del fluido sono
imposti essenzialmente da cause meccaniche (una pompa, nel caso di circolazione
dell’acqua, o semplicemente l’azione del vento), il fenomeno prende il nome di convezione
forzata. Ad esempio si ha convezione quando tra due corpi circola un fluido
intermedio (detto fluido termovettore), che si riscalda per conduzione a
contatto con il corpo caldo, e poi cede il calore quando viene a contatto con
il corpo freddo. In entrambi i casi, la quantità di calore scambiata è
proporzionale alla differenza di temperatura.
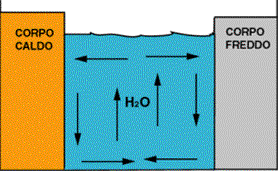
Fig. 2 moto molecolare nel mezzo
convettivo (in questo caso acqua)
Irraggiamento
Nell’irraggiamento
il calore viene scambiato mediante emissione e assorbimento di radiazione
elettromagnetica. Il calore così scambiato aumenta molto rapidamente con la
differenza di temperatura.
A
differenza delle altre due modalità di scambio termico, l’irraggiamento non richiede
la presenza di un mezzo perché vi sia trasmissione di energia. La radiazione
elettromagnetica che opera da "trasmettitore"di calore, è generata
dall’eccitazione termica della superficie del corpo, a sua volta causata dallo
stato energetico degli atomi che la costituiscono, ed è emessa in tutte le
direzioni.
Quindi
in questo caso il corpo avente temperatura maggiore emette radiazioni
elettromagnetiche che vengono assorbite dal corpo più freddo, come si vede
in figura 3 (nella figura sono
rappresentate soltanto le radiazioni termiche che investono il corpo freddo).
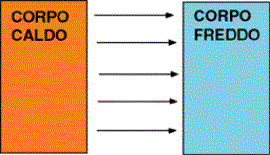
Fig. 3
Processi
di trasferimento di calore combinati
La
conduzione è il solo metodo di trasmissione nei solidi, mentre nei liquidi è
sempre accompagnata dalla convezione. Nei fluidi trasparenti il trasporto del
calore avviene tramite irraggiamento e convezione, mentre nei fluidi densi
l’irraggiamento è accompagnato dalla conduzione.
A
seconda della natura dei corpi in gioco nel fenomeno di trasmissione del
calore, assume un ruolo predominante una modalità rispetto alle altre, oppure
il calore viene trasferito grazie all’azione combinata di due o di tutte e tre
le modalità. Questo è causato dalle caratteristiche fisiche, ad esempio dalla
densità del corpo oppure se questo è più o meno trasparente. Ad esempio il
calore, dissipato attraverso le pareti interne di un edificio verso l’ambiente
esterno, attraversa per conduzione i vari strati che costituiscono la parete e
per convezione e irraggiamento gli spazi tra i mattoni occupati dall’aria. Una
volta che il calore ha raggiunto l’ambiente esterno, esso è dissipato tramite
convezione e irraggiamento. In un forno metallurgico, un metallo che viene
portato ad un’alta temperatura, è soggetto all’azione combinata delle tre
modalità. Il calore viene trasferito per conduzione attraverso la parte
dell’oggetto che è a contatto con la superficie del forno, mentre le altre zone
del metallo sono riscaldate per conduzione ed irraggiamento. Si nota che i tre
meccanismi agiscono come se fossero in serie e in parallelo, e questa loro
combinazione fornisce l’energia termica totale trasferita da un sistema
all’altro.
Consideriamo, come mostrato in figura 4a, due
corpi A e B a temperature diverse in una stanza contenente aria. Dal principio
zero della termodinamica sappiamo che il calore passa spontaneamente dal corpo
più caldo a quello freddo fino a che entrambi non hanno raggiunto la stessa
temperatura. Il calore in questo caso è scambiato per convezione ed
irraggiamento. Se fosse creato il vuoto nella stanza allora si avrebbe solo il
fenomeno dell’irraggiamento, e di conseguenza sarebbe scambiata tra i due corpi
una quantità minore di calore. Dopo un certo tempo, la potenza termica totale è
data dalla somma della potenza scambiata per convezione e per irraggiamento:
(1)
I
due meccanismi di trasmissione agiscono in parallelo. Si può stabilire una
analogia con i circuiti elettrici, e di conseguenza il fenomeno può essere
descritto dal circuito in figura 4b.
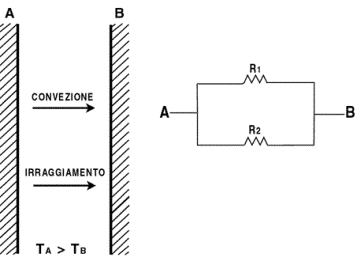
Fig.4a Fig.4b
Il
flusso di corrente che circola nelle due resistenze R1 e R2,
che indicano rispettivamente le resistenze di convezione ed irraggiamento, si
comporta in maniera del tutto analoga alla quantità di calore che fluisce per
un certo periodo tra i due corpi a causa della convezione e l’irraggiamento.
Infatti il flusso di corrente totale è dato dalla somma delle correnti che
circolano nelle due resistenze, cosi come la potenza termica totale era data
dalla somma delle potenze termiche scambiate dai singoli meccanismi di
trasmissione: vedi equazione (1).
Ci
sono altri casi in cui lo scambio termico può essere accostato ad un circuito
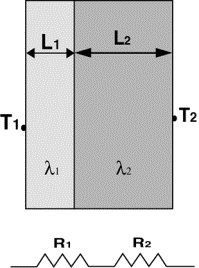
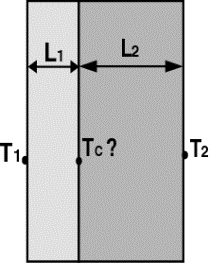
elettrico avente resistenze in serie. Consideriamo a tale proposito una parete
costituita da tre strati di materiale differente aventi le due superfici
parallele A e B a temperature diverse, come mostrato in figura 5a.
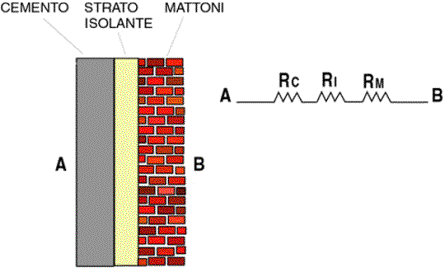
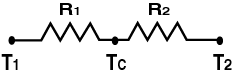
Fig. 5a (parete edile) Fig.5b
Il
calore, che è scambiato unicamente per conduzione, fluisce dalla parete A alla
B (TA > TB), e durante il suo cammino
incontra tre materiali diversi. In questo caso non si ha un unico fenomeno di
conduzione ma se ne hanno tre, uno per ogni materiale incontrato. Per analogia
possiamo considerare i tre strati come tre resistenze poste in serie (figura
5b), in quanto la potenza termica totale non è la somma delle tre singole
potenze ma segue la relazione:
(2)
dove 
, 
, e 
sono le potenze termiche
trasmesse per conduzione rispettivamente attraverso il cemento, lo strato
isolante e i mattoni.
Come
si nota dalla (2) la potenza termica totale trasferita è minore di quella che
fluirebbe singolarmente in ciascun materiale. I muri delle abitazioni sono
costituti da più strati proprio per minimizzare il calore disperso attraverso
essi.
Se
al posto delle potenze termiche sostituiamo delle correnti, ciò che si ottiene
è la corrente totale che scorre in un circuito costituto da tre resistenze in
serie.
Equivalente termico della legge
di Ohm
Le
considerazioni sulle analogie tra i fenomeni di scambio di calore circuiti
elettrici, e in particolare l’esatta corrispondenza tra potenza termica e
corrente elettrica, sono del tutto confermate dall’esistenza di una legge
fisica chiamata equivalente termico della Legge di Ohm. Essa afferma che
la quantità di calore scambiata nell’unità di tempo, ossia la potenza termica,
è direttamente proporzionale alla differenza di temperatura che causa lo
scambio di calore. In simboli:
(3)
dove ΔT è la
differenza di temperatura presente misurata in kelvin e 
è la potenza termica.
Con
il simbolo RT si è indicata la resistenza termica, la cui
definizione segue direttamente dalla (3):
(4a) 
(4b)
La
resistenza termica, a differenza di quella elettrica che possiede una propria
unità di misura nel Sistema Internazionale detta Ohm (1W=1V/1A), come mostrato nella (4b), si
misura in [K]∙[W]-1. Essa svolge nei confronti del flusso
termico e della differenza di temperatura, il medesimo ruolo che la resistenza
elettrica ha nei confronti rispettivamente della corrente e della differenza di
potenziale.
Per
fissare le idee sull’analogia tra fenomeni di scambio di calore e circuiti
elettrici, nella tabella 1 sono state accostate le loro grandezze fisiche e le
due leggi che le legano:
|
|
|
|||
|
Potenza
termica ( |
||||
)tab. 1-
Analogie tra elementi elettrici e
processi di scambio di calore.
Conduzione
Approfondiamo
ora il nostro studio sulla conduzione, enunciando le relazioni matematiche che
la regolano.
I processi
di scambio termico tramite conduzione sono generalmente classificati in:
·
Processi stazionari
·
Processi non stazionari o transitori
I primi
hanno la caratteristica che tutte le grandezze fisiche (temperatura, pressione,
etc.) in ogni punto della regione dove si ha conduzione sono indipendenti dal
tempo; al contrario i processi transitori implicano variazioni temporali che il
più delle volte interessano la temperatura. Inoltre la legge che descrivere i
processi stazionari, non è valida per quelli transienti. Per quest’ultimi, come
vedremo in seguito, useremo delle relazioni opportune.
Legge di Fourier
Prima di
enunciare la legge illustriamo le grandezze fisiche in gioco in un processo di
scambio di calore per conduzione.
La
quantità di calore trasmessa nell’unità di tempo per conduzione attraverso un
materiale solido, o equivalentemente attraverso un fluido in quiete, è chiamata
potenza termica e si indica con 
. Nel sistema internazionale essa si misura in watt.
Ricordiamo che il calore, essendo una forma di energia, si esprime in joule e
che 1watt=1joule/1secondo.
Si
definisce densità di flusso termico 
la potenza termica
per unità di superficie. Le sue dimensioni, nel Sistema Internazionale, sono
quelle di una quantità di calore per unità di superficie. In simboli
(5)
Essa
è sostanzialmente l’intensità I definita in Acustica. Successivamente,
studiando il fenomeno dell’irraggiamento, indicheremo con ancora con I
l’ Intensità di irraggiamento, che è la
grandezza analoga alla densità di flusso termico.
Possiamo
ora enunciare la legge di Fourier:
(6)
Essa
esprime la proporzionalità tra la densità di flusso di calore 
e il gradiente di
temperatura, dove:
·
grad ( ), indicato anche con 
(nabla), è un operatore vettoriale
che trasforma una funzione delle coordinate di un punto in un vettore le cui
componenti cartesiane sono le derivate parziali della funzione in quel punto.
·
T(x,y,z,t) rappresenta il campo scalare delle temperature all’interno di un
volume V di un corpo dove avviene conduzione; questo campo è variabile sia
nello spazio che nel tempo. La sua derivata spaziale rappresenta un vettore che
in ogni punto è diretto verso le temperature crescenti. Il vettore gradiente è
così perpendicolare alle superfici isoterme, orientato nel verso dell’isoterma
maggiore. Il suo modulo è proporzionale ala velocità di variazione della
temperatura nello spazio: quanto più le isoterme sono fra loro vicine, tanto
più alto sarà il gradiente e quindi, per la legge di Fourier, tanto più grande
sarà lo scambio termico. Nell’equazione (6) compare il segno meno perché il
verso del vettore gradiente è quello delle temperature crescenti, mentre il
vettore densità di calore ha verso concorde con quello delle temperature
decrescenti (il calore va dai corpi a temperatura più alta a quelli a
temperatura più bassa).
Quella appena considerata
è un’equazione vettoriale, per cui sia 
che il gradiente sono
due vettori, di solito con la stessa direzione, per cui ci interessa per lo più
valutarne il modulo.
La proporzionalità tra
densità di flusso termico e gradiente di temperatura, è espressa dal termine λ che prende il nome di conducibilità termica.
Quest’ultima, che non è grandezza vettoriale, è caratteristica del materiale
conducente il calore e dipende dalla sua natura e dal suo stato fisico. Dalla
legge di Fourier ricaviamo che λ, nel Sistema
Internazionale, si misura in 
.
Tramite i
valori della conducibilità termica è possibile classificare i materiali tra isolanti
termici, che hanno solitamente λ<1, e conduttori
termici. Sono detti isolanti quei materiali che ostacolano il passaggio del
flusso termico. L’isolante migliore è l’aria, che ha λaria=0.024 W/m
K. La lana di vetro, pur avendo un λ non troppo piccolo è
utilizzato come isolante. Questo materiale ha la proprietà di trattenere nel
suo interno aria, che funge da isolante.
I conduttori migliori sono i
metalli e le loro leghe, ad esempio il rame ha λCu=395 W/m K
e l’alluminio λAl=210
W/mK.
Per
una lista completa con molti valori di
conducibilità termica per diversi materiali si veda la tabella A in appendice.
La conducibilità termica per un dato materiale
dipende dal suo stato fisico e può variare con la pressione e la temperatura.
Mentre nella maggior parte dei casi, l’effetto della pressione è trascurabile, λ
è sempre funzione della temperatura, e varia
linearmente con essa.
Ad esempio, al crescere della temperatura, alcuni
materiali isolanti aumentano la loro conducibilità, mentre certi conduttori, a
causa della rottura dei legami cristallini perdono proprietà di condurre
calore. La legge di Fourier è valida anche in queste condizioni; risulta
soltanto di più difficile applicazione. In questo caso, per risolvere un
problema di scambio di calore, che ha come incognite le temperature, dobbiamo
iterare la soluzione. Dobbiamo cioè
procedere per tentativi assegnando valori arbitrari della temperatura, con i
quali ricaviamo le relative λ dalle tabelle come quella in appendice.
Risolviamo poi il problema con questi dati , calcoliamo le temperature e le
confrontiamo con quelle da noi assegnate arbitrariamente. Se sono uguali allora
quella è la soluzione. In caso contrario ripetiamo il procedimento fino a che
il risultato non si è stabilizzato.
La dipendenza della conducibilità dalla temperatura è
una funzione lineare:
(7)
λ0 è la
conducibilità a t=0°C e B è la variazione di λ0 per grado centigrado. Normalmente B è trascurabile
rispetto a λ0 cosicché λ risulta essere costante e siamo autorizzati
ad omettere la sua dipendenza dalla temperatura. Questa approssimazione è del
tutto lecita nei problemi pratici: infatti la termocinetica è una scienza
inesatta, in quanto si commettono errori anche del 20-30%.
Equazione di Fourier
La legge di Fourier è
utilizzata nei problemi di trasmissione del calore per trovare un’espressione
che descrive il campo termico in corpo. Tale legge però è valida solo
nell’ipotesi di operare in un campo termico in regime stazionario. Questo
significa che la temperatura rimane costante nel tempo. Mentre se essa varia,
se in altre parole analizziamo un campo in regime transitorio, la legge di
Fourier non descrive correttamente il processo. Partendo da questa legge, è
stata ricavata un’equazione differenziale di secondo grado, detta equazione
di Fourier, che fornisce una descrizione completa dell’evoluzione della
temperatura in funzione del tempo. Equivalentemente avevamo in acustica la
legge di Eulero, da cui si costruisce l’equazione di D’Alambert, e nel moto dei
fluidi la legge di Newton, che sta alla base dell’equazione di Navier. Mentre
nei casi citati, il passaggio dalla legge fisica all’equazione non aveva
sviluppi pratici, nel caso dello scambio termico passare dalla legge fisica
alla relativa equazione di Fourier può avere una qualche utilità pratica,
perché i problemi di scambio termico per conduzione si risolvono tramite
integrazione numerica dell’equazione di Fourier.
Come la
maggior parte delle equazioni fisiche, l’equazione di Fourier è una equazione
differenziale e come tale fornisce una soluzione generica; essa necessita
dell’imposizione delle cosiddette condizioni al contorno affinché possa
applicarsi al caso che stiamo trattando.
Le
condizioni al contorno sono di due tipi: spaziali e temporali.
Spesso le condizioni al
contorno sono di temperature imposte, cioè si devono risolvere problemi nei
quali è stata fissata la temperatura. In questo caso le condizioni al contorno
sono dette di tipo T.
Esiste un’altra categoria
di problemi nei quali invece è fissata la quantità di calore scambiata nel
tempo. Avremo allora condizioni di tipo Q.
Metodo per
ricavare l’equazione di Fourier
Partendo da un caso particolare (l’esempio sotto descritto),
ricaviamo l’equazione generale che regola i processi di conduzione, chiamata
equazione di Fourier.
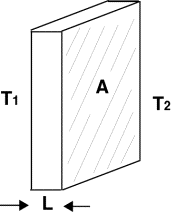
Consideriamo una lastra di
spessore costante L che abbia larghezza e lunghezza tanto grandi da potere
essere considerate infinite, vedi figura 6. In queste condizioni, la lastra
rappresenta un sistema monodimensionale dipendente dalla sola variabile x se
questa è inserita in un opportuno sistema di riferimento cartesiano. Supponiamo
che le pareti siano rispettivamente alla temperatura T1 e T2.
Consideriamo un elemento
della lastra di superficie A=1 m2 e spessore dx (nella figura 6 è
rappresentato dal rettangolo grigio). Inoltre supponiamo che la parete sia
costituita da un materiale avente densità volumetrica pari a ρ e assumiamo che λ, la sua conducibilità termica, sia costante.
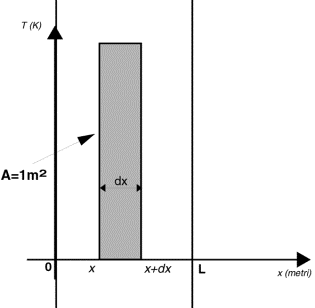
Fig.6 Lastra indefinita
Il volume dell’elemento
grigio evidenziato in figura è:
(8)
La massa di tale volume,
conoscendo la densità volumetrica è:
(9)
Supponiamo che al tempo τ=τ0 il sistema sia alla
temperatura T(x,τ0); il campo delle temperature è dipendente dal tempo, quindi dopo una
frazione di tempo dτ
la temperatura del sistema vale 
.
Sinteticamente:
Tx
= T(x,τ0)
Cioè gli istanti temporali
τ0 e τ0+dτ e le
corrispondenti temperature T(x,τ0) e T(x,τ0+dτ), sono associate rispettivamente alle ascisse x
e x+dx. In altre parole dτ
è la frazione di tempo che il calore impiega a percorre il tratto dx,
indicato in figura 6.
Possiamo fare un bilancio
dell’energia che entra all’ascissa x e di quella che esce all’ascissa
x+dx
, cioè attraverso lo spessore dx della lastra, utilizzando il primo
principio della termodinamica:
(10)
dove
chiaramente Q non è la potenza termica ma è la somma della quantità di calore
che entra in x e di quello che
esce in corrispondenza di x+dx.
Abbiamo
trascurato il temine relativo al lavoro, in quanto si tratta di un problema di pura
conduzione che, nella maggior parte dei casi avviane attraverso corpi solidi;
possiamo quindi trascurare eventuali deformazioni dovute alla compressione o
alla dilatazione. In poche parole il volume è costante e di conseguenza il
lavoro è nullo.
Per
esprimere la (10) in termini di densità di flusso termico dobbiamo moltiplicare
il secondo membro per dτ,
che rappresenta il tempo necessario affinché il calore fluisca nello spessore
considerato. Otteniamo quindi:
(11)
Scrivendo
l’energia ΔU in un funzione
della differenza di temperatura dT :
(12)
dove c rappresenta
il calore specifico del materiale (per un solido 
, cioè il calore specifico a
pressione e a volume costanti sono equivalenti).
Sostituendo
la (9) nella (12) si ha:
(13)
Utilizziamo
ora la legge di Fourier, espressa dalla relazione
(6)
per scrivere in altro modo
le densità di flusso termico che appaiano nel secondo membro della (13) e
applichiamo il gradiente ottenendo così:
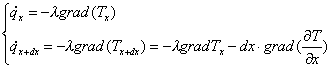(14)
Risolvendo
il sistema si ha:
(15)
semplificando:
(16)
La
(16) è l’equazione di Fourier.
Scritta
nella forma più generale, ossia in tre dimensioni:
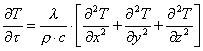(17a)
oppure,espressa
sinteticamente tramite l’operatore
(nabla quadro):
(17b)
L’equazione
nella forma generale, si applica quando si ha a che fare con una trasmissione
di calore per conduzione in regime transiente che avviene in tre dimensioni.
Mentre se siamo in regime stazionario, cade
la dipendenza dal tempo cosicché la derivata di questa grandezza è nulla.
L’equazione che risulta è chiamata equazione di Laplace:
(18)
Ipotizzando
che il caso trattato finora (figura 6) si svolga in regime stazionario, la (16)
diventa:
(19)
Integriamo
la (19) due volte, ottenendo:
(20)
le costanti A e B si
ricavano dalle condizioni al contorno:
x=0 T(0)=T1
x=L T(L)=T2
(21)
(22)
(23)
(24)
(25)
Esercizio 1
|
|
Esercizio 2
|
|
|
(4a)
e poiché 
(E1.1)
Esercizio 3
|
|
|
|
|
(E3.1)
(E3.2)
(E3.3)
(E3.4)
Appendice
Tabella A
MATERIALE |
Conducibilità termica a 20° C
(W/mK) |
|
Acciaio
con 5% Ni |
29 |
|
Acciaio
con 30% Ni |
105 |
|
Acqua
(liquida in quiete a 20°C) |
0,63 |
|
Acqua
pesante 10 ¸ 100°C |
0,56 ¸ 0,65 |
|
Alcool |
0,21 |
|
Alluminio |
210 |
|
Aria (in
quiete a 20°C) |
0,026 |
|
Argentana |
27 |
|
Argento |
420 |
|
Asfalto |
0,64 |
|
Basalto |
1,27 ¸ 3,5 |
|
Bronzo |
58 ¸ 65 |
|
Carbone |
0,14 ¸ 0,17 |
|
Carbone
di storta |
4 |
|
Carbone
in polvere |
0,12 |
|
Cartone |
0,14 ¸ 0,23 |
|
Cartongesso
in lastre |
0,21 |
|
Caucciù |
0,13 ¸ 0,23 |
|
Celluloide |
0,35 |
|
Cellulosa
compressa |
0,24 |
|
Cemento
in polvere |
0,070 |
|
Cenere |
0,069 |
|
Creta |
0,90 |
|
Duralluminio |
160 |
|
Ferro
elettrolitico |
87 |
|
Ferro ed
acciaio |
46,5/58 |
|
Gesso |
0,5 |
|
Ghiaccio |
2,20/2,50 |
|
Ghisa |
50 |
|
Glicerina |
0,220 |
|
Grafite |
4,9 |
|
Granito |
3,18 ¸ 4,10 |
|
Incrostazioni
di caldaia |
1,16 ¸ 3,49 |
|
Intonaco
di calce e gesso |
0,70 |
|
Legno
asciutto ^ alle
fibre di abete
e pino |
0,10 ¸ 0,12 |
|
Legno
asciutto ^ alle
fibre di
quercia |
0,18 |
|
Legno
asciutto parallelamente alle
fibre |
0,15 ¸ 0,27 |
|
Linoleum |
0,18 |
|
Manganina |
23 |
|
Marmo |
2,1 ¸ 3,5 |
|
Mercurio
liquido a 0° C |
8,13 |
|
Mercurio
liquido a 60° C |
9,64 |
|
Mercurio
liquido a 120° C |
10,92 |
|
Mercurio
liquido a 160° C |
11,6 |
|
Mercurio
liquido a 222° C |
12,78 |
|
Mica |
0,39 |
|
Muratura
di pietrame |
1,40 ¸ 2,40 |
|
Muratura
refrattaria (dinas,
schamotte, silica) 200° C |
0,70 ¸ 0,90 |
|
Muratura
refrattaria (dinas,
schamotte, silica) 1000° C |
1,2 ¸ 1,4 |
|
Naftalina |
0,37 |
|
Neve
(appena caduta e per strati fino a 3 cm) |
0,06 |
|
Neve
(soffice, strati da 3 a 7 cm) |
0,12 |
|
Neve
(moderatamente compatta, strati da 7 a 10 cm) |
0,23 |
|
Neve
(compatta, strati da 20 a 40 cm) |
0,70 |
|
Nichel |
58 ¸ 65 |
|
Oli e
petroli |
0,12 ¸ 0,17 |
|
Oro |
299 |
|
Ottone |
70 ¸ 116 |
|
Pietra
arenaria |
1,30 ¸ 1,75 |
|
Pietra
calcare compatta |
0,70 |
|
Pietra
calcare granulosa |
0,95 |
|
Piombo
solido |
35 |
|
Pb 44,5%
+ Bi 55,5% (lega liq.) 160 ¸ 320° C |
9,2 ¸ 11,3 |
|
Platino |
70 |
|
Porcellana |
0,80 ¸ 1,05 |
|
Quarzo ^
all’asse |
6,60 |
|
Quarzo
parallelo all’asse |
12,80 |
|
Quarzo
oggetti fusi |
1,4 ¸ 1,9 |
|
Rame (8300 Kg/m3) |
302 |
|
Rame (8900 Kg/m3) |
395 |
|
Sabbia
asciutta |
0,35 |
|
Sabbia
con 7% di umidità |
1,16 |
|
Sodio
solido |
125,60 |
|
Sodio
liquido 100 ¸ 500° C |
86 ¸ 67 |
|
Na 56% +
K 44% (lega Na, K liq.) 100 ¸500°C |
27 |
|
Stagno |
64 |
|
Steatite |
2,7 |
|
Sughero
(200 Kg/m3) |
0,052 |
|
Vetro |
0,5 ¸ 1 |
|
Wood
(lega) |
12,78 |
|
Zinco |
110 |
|
Zolfo |
0,23 |