Studio della propagazione del rumore in ambienti industriali bassi e vasti

Introduzione

E' noto che la propagazione del rumore in ambienti industriali bassi e vasti avviene con modalità sostanzialmente diverse da quelle solitamente verificate in ambienti più regolari; in particolare, le ipotesi dell'acustica statistica (formulazione di Sabine) non sono rispettate, ed il decadimento del livello sonoro con la distanza dalla sorgente esibisce un andamento fortemente divergente da quello ottenibile dalla classica formulazione del campo semi-riverberante.

La conseguenza di quanto sopra è duplice: da un lato, nel caso di rilievi della potenza sonora di macchinari secondo ISO 3744/46 e norme derivate, oppure del livello sonoro al posto operatore secondo le norme della serie ISO 11200, il fattore di correzione ambientale K viene drasticamente sottostimato allorquando lo stesso viene calcolato sulla base delle unità assorbenti stimate a partire dal tempo di riverberazione del locale tramite la formula di Sabine. Dall'altro, il beneficio ottenibile da interventi di trattamento fonoassorbente dei locali, ed in particolare della copertura, viene anch'esso fortemente sottostimato, con il risultato che sovente si sconsiglia il trattamento di questi ambienti, quando invece i risultati conseguibili sono notevoli.

Nel presente lavoro si è operato su due diversi fronti: rilievi sperimentali e simulazioni numeriche. Nel primo caso si è fatto ricorso ad avanzate tecniche di misura, ivi incluso il rilievo di potenza con tecnica intensimetrica (ISO 9614/2) e la misura del decadimento del livello sonoro con la distanza (progetto di norma UNI U20.00.054.0).

Si è poi operata la simulazione numerica della propagazione del rumore in uno dei 4 stabilimenti studiati sperimentalmente, facendo uso di un codice di calcolo di tipo "pyramid tracing": tale algoritmo è applicabile anche ad ambienti fortemente non Sabiniani, quali quelli qui studiati.

Dall'analisi dei risultati ottenuti, è stato possibile evidenziare il tipico comportamento degli ambienti industriali bassi e larghi, e quantificare l'errore che si commette impiegando le classiche relazioni derivate dalla teoria di Sabine per stimare il contributo del campo riverberante al livello sonoro in ciascun punto.

E' stato inolte possibile ricavare una semplice espressione empirica per la stima di un Volume ridotto dell'ambiente, che introdotta nelle relazioni già previste dalle norme ISO per la stima delle unità assorbenti del locale e del fattore di correzione ambientale K, consente di minimizzare l'errore commesso nell'impiego delle stesse, pur consentendo il rispetto formale delle norme ISO.

Teoria classica (Sabine)

La classica formulazione teorica valida in ambienti che obbediscono alle ipotesi di Sabine è riassumibile nelle seguenti 3 equazioni

· (1)

· (2)

· (3)

In cui T è il tempo di riverberazione, V il volume dell'ambiente, A la superficie totale delle pareti dello stesso, il coeff. di assorbimento acustico medio, d la distanza del punto di ascolto dal centro acustico della sorgente, ed S la superficie di inviluppo utilizzata per la misura del livello di potenza sonora.

Queste relazioni sono fra loro congrue nell'ipotesi che una sorgente puntiforme omnidirezionale, di livello di potenza costante L_W, venga posta a breve distanza da un pavimento riflettente, cosicchè il fattore di direttività Q risulti pari a 2, e la superficie S di inviluppo venga assunta uguale a quella di una semisfera di raggio d.

Tale formulazione è abbastanza accettabile solo in ambienti che obbediscono strettamente alle ipotesi di Sabine, le quali richiedono che le tre dimensioni dell'ambiente siano fra loro confrontabili, che non vi siano ostacoli all'interno del volume, e che il coefficiente di assorbimento acustico delle pareti sia ovunque poco discosto dal valore medio . In tali ipotesi, il libero cammino medio dei raggi sonori approssima il valore teorico:

(4)

Quando viceversa una delle tre dimensioni del locale è significativamente inferiore alle altre 2 (nel nostro caso l’altezza h), il libero cammino medio tende a risultare poco maggiore di tale dimensione minima, indipendentemente dal volume complessivo. Sperimentalmente si verifica che il livello sonoro cala incessantemente all’aumentare della distanza d, mentre in base alla relazione (2) esso dovrebbe tendere a stabilizzarsi ad un valore costante. Inoltre si verifica che a distanze dalla sorgente dell’ordine di 5-15m (tipiche di rilievi su macchine di dimensioni rilevanti), il fattore di correzione ambientale K risulta sottostimato anche di 4-5 dB.

Non sono mancati studi teorici sulla propagazione del rumore in ambienti bassi, tuttavia gli stessi erano finalizzati principalmente alla individuazione della legge di decadimento del livello sonoro (espressa in dB per raddoppio della distanza), e non alla stima del fattore di correzione ambientale K.

Rilievi sperimentali

Al fine di ottenere sperimentalmente il fattore di correzione ambientale K in ambienti bassi e vasti, si è adottata una procedura combinata che prevedeva i seguenti punti:

· Impiego di una sorgente omnidirezionale (dodecaedro) di potenza sonora nota (110 dBA), alimentata con rumore rosa

· Misurazione simultanea del livello di potenza sonora della stessa su una superficie di inviluppo standardizzata (5.4x5.4x2.7m), mediante le metodologie ISO 3746 (pressione) ed ISO 9614/2 (intensimetria)

· Misurazione del decadimento del livello sonoro con la distanza secondo norma UNI U20.00.054.0

· Misura del tempo di riverberazione dell'ambiente secondo ISO3382 (risposta all'impulso ottenuta con tecnica MLS, integrazione all'indietro di Schroeder ed estrapolazione del tratto di decadimento sonoro compreso fra -5 e -25 dB)

· Verifica pratica mediante misurazione in condizioni operative del livello di potenza sonora di una o più macchine, impiegando simultaneamente sia la tecnica intensimetrica che il tradizionale rilievo in pressione sonora.

Tranne l'ultimo rilievo in condizioni operative, tutti gli altri rilievi sono stati eseguiti a stabilimento fermo, con rumore di fondo trascurabile rispetto a quello emesso dalla sorgente di prova.

La seguente tabella riporta i principali dati relativi ai 4 stabilimenti studiati:

Nome	V (m³)	H (m)	T_med(s)	K_sperim(dBA)	K_Sabine(dBA)
Thessaloniki	48836	8.3	2.60	2.40	0.48
Pelfort	72000	11.92	2.45	1.45	0.48
Patrasso	32000	8.0	3.50	2.75	0.51
Fredericia	27575	7.62	0.80	1.45	0.40

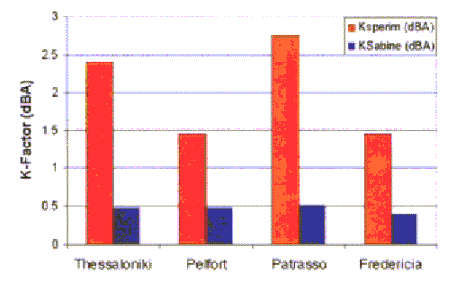
Tab 1, Fig 1 – Riepilogo dei rilievi eseguiti

Il valore “sperimentale” del fattore di correzione ambientale K_sperim, riportato nella tabella, è il risultato della differenza fra il livello di potenza misurato secondo la norma ISO3746 (senza applicazione del fattore K teorico) e quello misurato secondo ISO9614/2 (che è di sua natura immune dal contributo della riverberazione del locale). Si nota che lo stesso è drasticamente superiore al valore riportato nell’ultima colonna della tabella, ottenuto dalla applicazione della applicazione della formulazione di Sabine classica, sulla base dell’eq. (3).

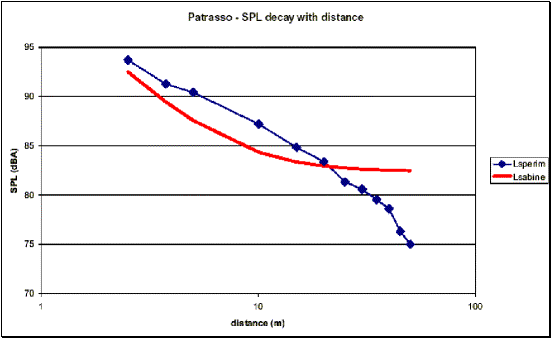
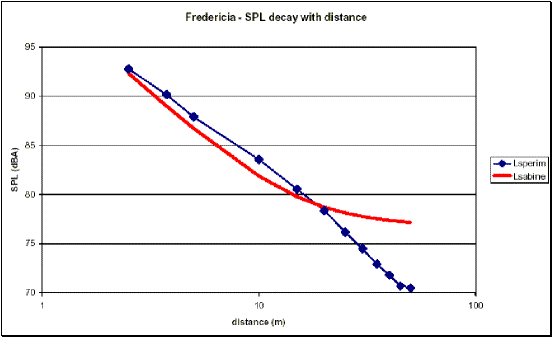
Le seguenti 4 figure mostrano il confronto fra i livelli sonori in funzione della distanza ottenuti sperimentalmente e quelli ricavati dalla relazione (2):

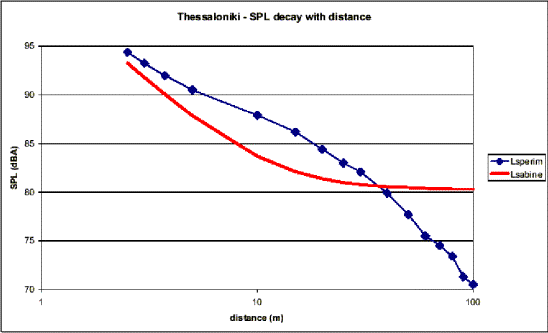
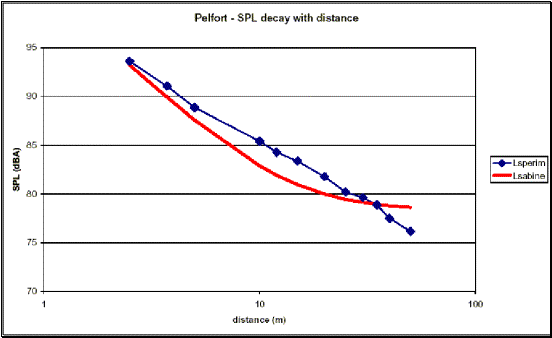
Figure 2,3,4,5 – Confronto tra livelli sonori sperimentali e teorici (equazione (2)) in funzione della distanza

Si osserva come i tracciati siano sostanzialmente divergenti, e come a distanze dalla sorgente dell’ordine dei 5-15 m si verifichino differenze anche di 4-5 dB(A). Ciò significa che le formule basate sulla teoria di Sabine sottostimano in modo rilevante il contributo del campo sonoro riverberante prodotto da sorgenti sonore situate in questo range di distanze, e dunque sia il fattore di correzione ambientale, sia il contributo di sorgenti estranee a quella di oggetto di misura vengono drasticamente falsati, con il risultato che il livello di potenza sonora della macchina in esame viene sovrastimato.

Simulazione numerica

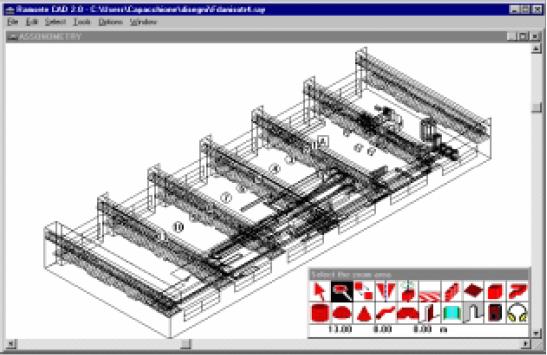
E' stata eseguita la simulazione numerica della propagazione del rumore nel caso dello stabilimento di Fredericia. La seguente figura illustra il modello CAD dell'ambiente stesso, usato per le simulazioni acustiche.

Figura 6 – Modello CAD dello stabilimento di Fredericia

I valori dei coefficienti di assorbimento dei materiali sono stati aggiustati manualmente, onde minimizzare lo scostamento fra i valori sperimentali e quelli calcolati dei tempi di riverberazione T₂₀ alle varie frequenze.

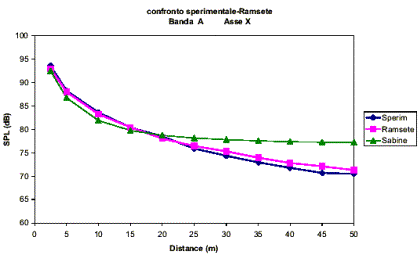
La seguente figura riporta il confronto fra i valori del livello sonoro rilevati sperimentalmente e calcolati dal codice di calcolo a varie distanze dalla sorgente.

Figura 7 – Confronto tra valori di livello sonoro rilevati sperimentalmente, teoricamente e con codice di calcolo

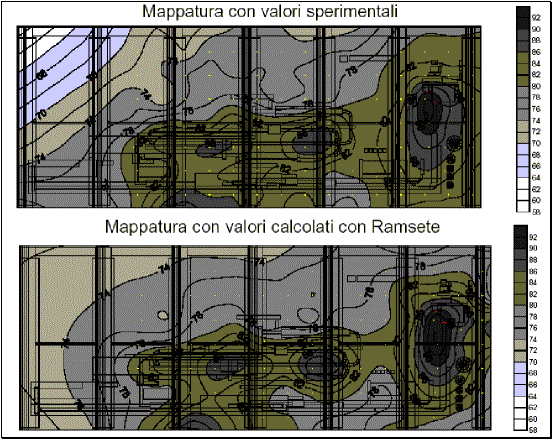
Si nota che l'accordo è molto buono. E' stata altresì eseguita la simulazione del funzionamento dell'intero stabilimento, introducendo nel modello numerico un adeguato numero di sorgenti sonore, caratterizzate da livelli di potenza ottenuti da rilievi sperimentali eseguiti sulle singole macchine effettivamente installate nello stabilimento. Il confronto fra la mappatura dei livelli sonori ottenuti sperimentalmente e quelli calcolati dal programma è visibile nella seguente figura.

Figura 8 – Confronto tra mappatura dei livelli sonori sperimentali e di quelli calcolati dal programma Ramsete

Anche se l'accordo non è così buono come nel caso della simulazione eseguita con la sola sorgente omnidirezionale di riferimento, comunque si è ottenuto un andamento della distribuzione del livello sonoro in discreto accordo con quella sperimentale, con un valore medio quadratico dell'errore di calcolo di 1.6 dB(A), e con errore massimo di 3.5 dB(A). Ci si attende un significativo miglioramento della precisione di calcolo dall'impiego di dati di emissione delle sorgenti sonore più raffinati, ottenuti mediante tecnica intensimetrica, comprendenti anche i "balloon" di direttività delle singole sorgenti.

E' comunque evidente da entrambe le simulazioni eseguite che l'algoritmo di pyramid tracing non ha di per se alcun problema nell'analisi di ambienti bassi e vasti, e consente dunque di valutare le condizioni di propagazione e stimare correttamente il valore del fattore di correzione ambientale K, note che siano la geometria dell'ambiente e le caratteristiche di fonoassorbimento delle superfici dello stesso.

L'attuale limite di impiego della simulazione numerica di ambienti industriali risiede soltanto nella mancanza di idonei dati in ingresso, in particolare sia per quanto riguarda le proprietà fonoassorbenti delle superfici, sia soprattutto per i livelli di potenza sonora e la direttività delle sorgenti, che per di più sono sovente variabili in funzione delle lavorazioni eseguite o della tipologia di prodotto trattato.

Entrambi questi problemi possono comunque essere risolti grazie all'impiego di avanzate tecniche di rilievo sperimentale in situ, facenti impiego dell'intensimetria acustica. E' stato infatti già mostrato come tramite questa tecnica si possa procedere al rilevamento in situ del coeff. di assorbimento acustico dei materiali ed alla esatta quantificazione della emissione sonora di una macchina, purchè il campo sonoro nell'ambiente resti stazionario nel corso del rilievi.

Formulazione empirica semplificata

Nonostante la tecnica di simulazione numerica impiegata abbia fornito risultati soddisfacenti, la stessa non può attualmente essere impiegata in modo generalizzato, sia per la mancanza di dati già delineata, sia per il tempo necessario alla modellizzazione geometrica di ambienti sovente molto complessi. Quest'ultimo fattore è solitamente la voce di costo più rilevante, in quanto la messa a punto della rappresentazione numerica tridimensionale dell'ambiente può risultare da sola più costosa dello stesso acquisto dello strumento di calcolo...

E' pertanto estremamente utile disporre di una formulazione empirica molto semplice, alternativa all'impiego delle formule basate sulla teoria di Sabine già illustrate, che consenta una stima del fattore di correzione ambientale K decisamente meno errata di quella ottenibile con queste ultime.

E' inoltre opportuno che tale formulazione si integri con le prescrizioni contenute nelle norme ISO 3744/46 ed 11203/4, dimodochè la stessa possa venire lecitamente impiegata nell'esecuzione di rilievi aventi valore legale in ambienti bassi e vasti. A questo proposito, la formula empirica qui proposta consente di mantenere valide le relazioni (1), per il calcolo del numero di unità assorbenti totali a partire dal valore sperimentale del tempo di riverberazione T, e (3), per il calcolo del fattore di correzione ambientale K. Il trucco consiste nell’introdurre nella (1), al posto del volume complessivo dell’ambiente, un volume ridotto V’, funzione dell’altezza del locale h e della distanza del punto considerato dalla sorgente d, ovvero della estensione della superficie di inviluppo S considerata:

(5)

formula empirica

Impiegando tale relazione per il calcolo del fattore di correzione ambientale K, si ottengono dei valori teorici in buon accordo con quelli rilevati sperimentalmente nei 4 stabilimenti studiati, come mostrato nelle seguenti 4 figure.

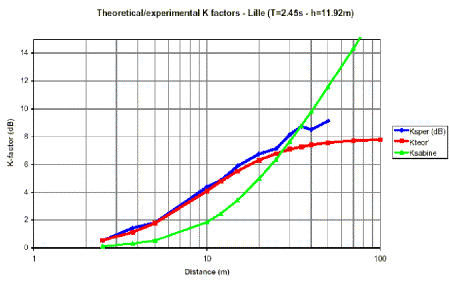
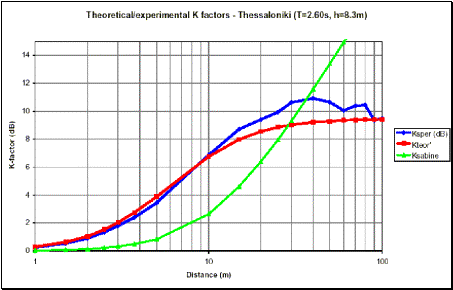
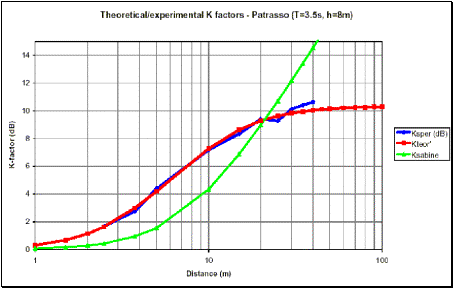
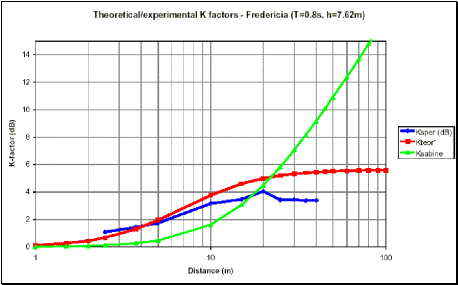
Figure 9,10,11,12 – Fattori K sperimentali, teorici (Sabine) e calcolati col volume ridotto V’ a confronto

Anche se l'accordo con i dati sperimentali non è perfetto ovunque, si osserva comunque una drastica riduzione dell'errore nella stima del fattore di correzione ambientale K rispetto all'impiego della formula di Sabine (1) con il volume complessivo dell'ambiente. L'accordo è molto buono soprattutto per distanze dalla sorgente comprese fra 5 e 10 m, che corrispondono ai casi più frequentemente incontrati nella pratica, mentre a distanze maggiori compare qualche scostamento, sicuramente dovuto alla particolare geometria degli ambienti ed alla presenza in esso di ostacoli o superfici schermanti/riflettenti, che ovviamente non vengono prese in considerazione dalla semplice formula empirica (5), e che invece, se correttamente introdotte in un modello di simulazione numerica, possono venire risolte come mostrato nel precedente paragrafo.

Normativa a tutela della salute negli ambienti di lavoro

Concetti generali

L’igiene del lavoro ha per scopo l’identificazione ed il controllo dei fattori di rischio relativi all’ambiente di lavoro al fine di assicurare il benessere dell’uomo nell’ambito del processo lavorativo.

Per “ambiente di lavoro” si intende lo spazio, nel quale si svolge l’attività lavorativa, caratterizzato da “fattori fisici” (clima, microclima, radiazioni ionizzanti e non, rumore, ultrasuoni e vibrazioni) e “fattori chimici” (sostanze allo stato corpuscolare e volatile).

Per “benessere” si intende il complesso ottimale delle condizioni ambientali – nell’ambito del processo lavorativo – in relazione alle componenti fisiologiche dell’uomo rapportate al tempo di esposizione.

Per ogni fattore fisico e chimico vengono stabilite correlazioni tra i “valori ammissibili relativi al fattore considerato” (detto anche “fattore di rischio”) ed i “tempi di esposizione” degli operatori; tali correlazioni sono stabilite in base a dati ricavati dall’esperienza operativa, o risultati di ricerche sperimentali sia su animali che sull’uomo.

I valori ammissibili dei fattori di rischio sono valori di riferimento per la progettazione igienica degli ambienti di lavoro.

Poniamo ora la nostra attenzione, nell’ambito di questa normativa d’igiene così complessa e variegata, sulle norme riguardanti il fattore fisico rumore.

Rumore

Effetti negativi del rumore

Danni a carico dell’udito, danni a carico di altri organi o della psiche, disturbo del sonno e del riposo, interferenza sulla comprensione della parola o di altri segnali acustici, interferenza sul rendimento, l’efficienza, l’attenzione, l’apprendimento, sensazione generica di fastidio. Per i danni a carico dell’udito nell’ambito dell’ambiente di lavoro, è di grande significatività il “livello equivalente continuo” del rumore, ponderato A, riferito alla durata normale dell’orario di lavoro (8 h/giorno, 5 giorni/settimana, 50 settimane/anno) e si indica con L_eq.

Rilevazione del rumore

Per i metodi di rilevazione e la strumentazione necessaria, prevista dalla normativa vigente, per indagini sul rumore negli ambienti di lavoro si veda la seguente tabella

Scopo dell’indagine

Metodiche da impiegare

Strumentazione

Acquisizione dei dati per la valutazione del rischio di danno uditivo

Valutazione del livello sonoro in dB(A) per lettura diretta

Valutazione del livello equivalente continuo

Misuratore sonoro (IEC 179)

Registratore magnetico professionale

Acquisizione dei dati per l’attuazione di provvedimenti di protezione acustica

Analisi spettrale del rumore per bande di ottava

Studio della disposizione e del contributo delle diverse sorgenti alla rumorosità globale

Studio delle caratteristiche acustiche del locale

Misuratore di livello sonoro continuo equivalente

Misuratore di livello sonoro con banco di filtri per bande di ottava o di 1/3 di ottava

Generatore di rumore bianco (per tempo di riverberazione)

Registratore magnetico professionale

Effettuazione dei controlli per accertare l’entità della dose di rumore assordante

Dosimetri individuali

Dosimetria del rumore in rapporto al tempo di esposizione

Individuazione del superamento di un livello di tetto precalcolato

Tabella 2 – Metodiche di rilevazione e strumentazione necessaria per indagini sul rumore negli ambienti di lavoro

Prevenzione da rumore

Principali provvedimenti per la prevenzione del danno da rumore nell’ambito dell’ambiente di lavoro:

riduzione rumore alla sorgente (riduzione di vibrazione d’urto, vibrazioni da sfregato, vibrazioni forzate, vibrazioni libere, risonanza mediante riduzione, equilibratura, ripartizione delle forze meccaniche, riduzione delle superfici radianti, riduzione dell’efficienza di emissione delle superfici vibranti ecc.),
intervalli sulle vie di trasmissione del rumore (incapsulamento sorgenti installazione schemi, isolamento basamenti ecc.),
interventi di protezione acustica dell’ambiente (isolamento di pavimenti, pareti, soffitti ecc., installazione di pannelli e strutture fonoassorbenti, cabine insonorizzate di telecomando delle macchine ecc.),
provvedimenti di protezione acustica individuale (cabine insonorizzate per il riposo silente degli operatori, cuffie antirumore, tappi auricolari, ecc.).

Il personale va sottoposto a controlli audiometrici periodici.

Aspetti normativi

Allo scopo di tutelare i lavoratori dai rischi di rumore il D.L. 277 del 15/8/91 concernente l’attuazione delle direttive CEE n. 80/1107, n. 82/605, n. 86/188 e n. 88/642 in materia di protezione dei lavoratori contro rischi derivanti da esposizione ad agenti chimici, fisici e biologici durante il lavoro. Il capo IV di tale decreto è interamente dedicato alla protezione dei lavoratori contro i rischi di esposizione a rumore durante il lavoro.

Conclusioni

Lo studio eseguito, svolto grazie ad una collaborazione fra SASIB Beverage ed Università di Parma, ha consentito di evidenziare il peculiare comportamento acustico degli edifici industriali bassi e vasti. Esso causa un rilevante contributo dovuto alle riflessioni sonore, che producono un innalzamento del livello sonoro complessivo ben superiore a quanto solitamente ipotizzato sulla base della teoria di Sabine. Tale effetto è particolarmente drammatico in quei comparti produttivi caratterizzati da numerose sorgenti sonore distribuite, legate a macchinari di trasporto (imbottigliamento, packaging), e contemporaneamente da posizioni degli operatori situate a distanze di alcuni metri dalle sorgenti sonore.

In ogni caso, comunque, la corretta valutazione dell'emissione sonora dei macchinari o dell'esposizione dei lavoratori viene alterata da tale meccanismo di propagazione, senza che i termini correttivi previsti dalle norme ISO di più comune impiego riescano a compensarlo adeguatamente.

I rilievi sperimentali hanno mostrato come la tecnica intensimetrica consenta la corretta stima del livello di potenza sonora, e come l'impiego di una sorgente sonora di riferimento (di potenza nota) consenta altresì di accedere direttamente al valore "vero" del fattore di correzione ambientale K. Tuttavia tali tecniche di rilievo sono costose e complesse, e probabilmente la maggior parte degli operatori continuerà ad usare semplici rilievi fonometrici ancora per molti anni.

E' stata anche valutata la possibilità di impiegare avanzati programmi di simulazione numerica per studiare la propagazione del rumore in ambienti industriali: i risultati sono stati incoraggianti, e mostrano come con tali strumenti si possa ottenere una ragionevole valutazione previsionale nel caso della progettazione di nuovi reparti produttivi. Il tempo richiesto è comunque risultato tuttora troppo elevato per l'utilizzo generalizzato di tali metodiche al semplice scopo di stimare il valore corretto del fattore di correzione ambientale K.

Sulla base dei dati rilevati sprimentalmente ed ottenuti dalle simulazioni numeriche, è stata pertanto derivata una semplice relazione empirica per la stima di un volume ridotto dell'ambiente, da introdurre nella relazione di Sabine onde "aggiustarla" nel caso di impiego in ambienti bassi e vasti. Tale relazione richiede semplicemente la conoscenza dell'altezza media del locale e della distanza del punto considerato dalla sorgente sonora, ovvero della superficie di inviluppo impiegata. Le dimensioni effettive in pianta dell'ambiente risultano così in pratica ininfluenti sul risultato.

L'impiego della relazione empirica qui presentata consente un significativo miglioramento della stima del fattore di correzione ambientale K, mantenendo comunque la più completa compatibilità con la formulazione prevista dalle norme tecniche vigenti.

Il proseguimento della ricerca consisterà nell'affinamento delle tecniche di simulazione numerica, ed in particolare nel rilevamento di dati di ingresso per le simulazioni (assorbimento dei materiali, potenza sonora delle macchine) e nel miglioramento dell'interfaccia CAD, onde ridurre i tempi necessari alla modellazione geometrica dell'intero stabilimento.

Si cercherà inoltre una giustificazione teorica della relazione (5), sulla linea di quanto fatto a suo tempo per la formula di Sabine stessa, che dopo essere stata ricavata sulla base di risultati sperimentali, è stata giustificata teoricamente solo dopo ulteriori, avanzati studi.

Esempio applicativo (1)

Si vuole valutare l’effetto di un trattamento ambientale in uno stabilimento basso e vasto. I dati di calcolo sono i seguenti:

· Sia S una sorgente di rumore puntiforme

· Sia r un ricevitore posto al centro dell’edificio

· L’ambiente sia semiriverberante con le seguenti dimensioni:

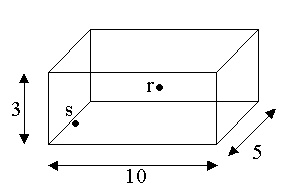
· Siano dati i seguenti coefficienti di assorbimento

· La potenza della sorgente sonora sia:

1. Si richiede di calcolare all'interno della stanza il livello di pressione al ricevitore L_p dovuto all’onda diretta.

2. Calcolare il livello di pressione dovuto all’onda riverberante.

3. Calcolare il livello di pressione totale al ricevitore.

Risoluzione

Per un ambiente semiriverberante vale la seguente formula per calcolare il livello di potenza dell’onda diretta:

(1)

Calcoliamo ora la distanza dalla sorgente sonora al centro della stanza

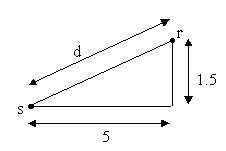
(2)

Il livello di potenza è dato da

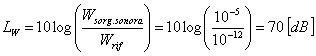(3)

Per la direttività Q, ricordiamo le seguenti possibilità

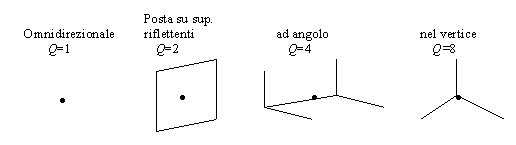
Valore della direttività a seconda della posizione della sorgente sonora

Quindi nel nostro caso

(4)

Sostituendo (2), (3) e (4) in (1) si ottiene il livello di pressione richiesto al ricevitore dovuto all’onda diretta

(5)

Prima di calcolare il livello di pressione dovuto all’onda riverberante, facciamo alcune osservazioni preliminari: guardando il grafico seguente

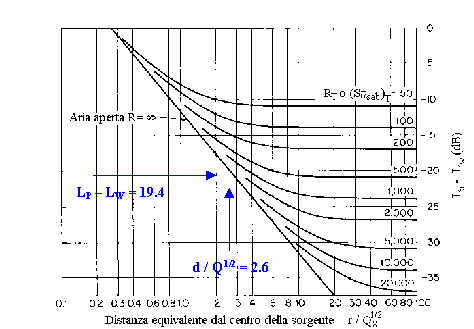
In un ambiente di questo tipo, non prevarrà l’onda diretta, ma anche una parte significativa di onda riverberante, ci si aspetta di ottenere un valore di livello di pressione maggiore di quello dovuto alla sola onda non-riverberante.

Procediamo dunque al calcolo del livello di pressione dovuto all’onda riverberante, utilizzando la seconda formula della teoria di Sabine.

(6)

dove A è definito come

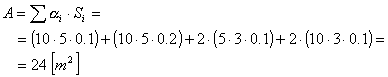
allora

(7)

Il livello di pressione totale risulta

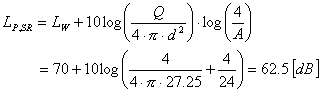(8)

Osservazione:

Il livello di pressione non si discosta molto da quello dovuto alla componente riverberante; si poteva quindi trascurare il contributo dell’onda diretta in quanto il livello di pressione è trascurabile rispetto a quello dovuto all’onda riflessa

D’altra parte, facendo la somma logaritmica di (5) e (7), si vede subito quanto appena asserito.

(9)

Supponiamo ora di avere un’altra sorgente sonora all’interno della stanza.

Per calcolare il livello di pressione totale al ricevitore si applica la sovrapposizione degli effetti:

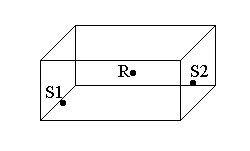
(10)

Esempio applicativo (2)

Ricavare il valore del coefficiente di assorbimento a_P di una superficie di prova posta in camera riverberante.

· Sia data una camera riverberante con le seguenti dimensioni:

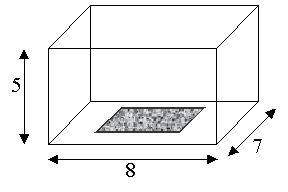
· Dimensioni della superficie di prova:

· I coefficienti di assorbimento delle pareti del soffitto e del pavimento sono uguali

· Il tempo di riverberazione quando la stanza è vuota è

· con la presenza della lastra di prova è invece

Risoluzione

Il tempo di riverbero è:

(1)

Da questo possiamo ricavare il coefficiente di assorbimento della camera.

(2)

Da notare che il valore ottenuto è molto basso in quanto la camera è riverberante e non vi è assorbimento.

Al momento del posizionamento della lastra si può scegliere di adagiarla su una superficie qualsiasi, poiché all’interno della camera riverberante il livello di pressione è uguale in ogni punto. In termini pratici, una volta posizionata la superficie di prova, viene modificato il valore del coefficiente di assorbimento equivalente.

(3)

A₂ viene calcolato dai dati iniziali

(4)

da (3) e da (4) si calcola infine il coefficiente della superficie di prova

(5)