Autore Giampiero Savalla - matr. 148465 - lezione del 26/11/2001 - ore 14-30 16-30

ACUSTICA NEGLI AMBIENTI CHIUSI

Abbiamo visto nei capitoli precedenti che data una sorgente S di suono  posta ad una certa distanza d dal ricevitore R, l’espressione che lega il livello di pressione al ricevitore è:

Lp = Lw – 20 log ( d ) – 11 + 10 log ( Q )                   (1)

  Dove con Q si indica la direttività della sorgente nella particolare direzione q, definita come il rapporto tra l’intensità emessa in una certa direzione e l’intensità media emessa in tutte le direzioni :

                                             (2)

In base al posizionamento della sorgente avremo ad esempio :

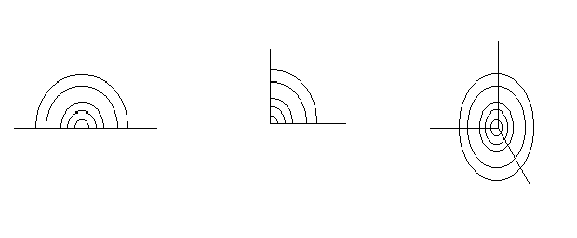
                Q = 2                                             Q = 4                                  Q = 8

Mentre in uno spazio aperto le onde emesse dalla sorgente si diramano in tutte le direzioni e giunge al ricevitore l’onda diretta (quell’onda il cui cammino si ottiene congiungendo idealmente con una retta, sorgente e ricevitore) in uno spazio chiuso la situazione risulta molto diversa.

  PROPAGAZIONE DEL SUONO IN UNA STANZA

  Supponiamo di trovarci in una stanza all’interno della quale si trova una sorgente omnidirezionale che emette  fronti d’onda sferici con uguale intensità in ogni direzione e un ricevitore R posto a distanza d dalla sorgente, come mostra la figura.

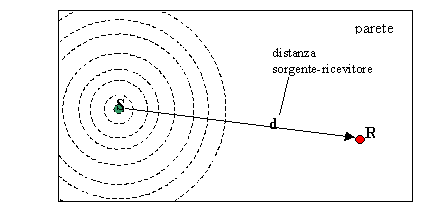
Anche in questo caso avremo un raggio che parte dalla sorgente e arriva direttamente al ricevitore, ma gli altri raggi, che prima si disperdevano nello spazio, adesso rimbalzano contro le pareti e arrivano lo stesso al ricevitore ma con un certo ritardo.

Di conseguenza oltre all’onda diretta dovremo considerare anche le onde riflesse e quindi la formula trovata per gli spazi aperti risulta inadeguata.

Se visualizziamo in un diagramma l’andamento dell’energia che giunge al ricevitore in funzione del tempo avremo un andamento del tipo :

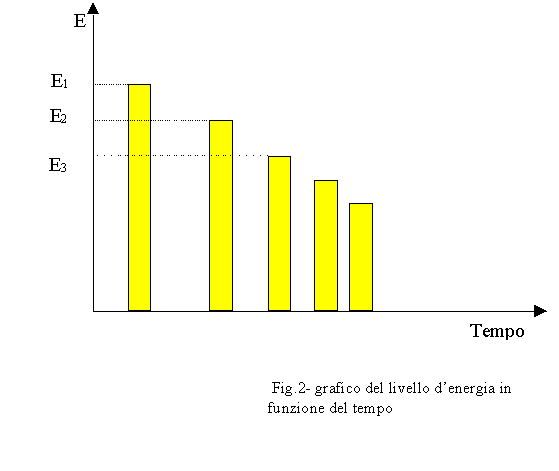
Dove E1 è dovuto al suono diretto, cioè il suono che ha percorso la minima distanza possibile tra sorgente e ricevitore senza aver subito alcun fenomeno di riflessione, mentre gli altri valori sono dovuti al suono che raggiunge il ricevitore dopo essere stato riflesso.

Si osservano fondamentalmente due cose:

1)      le intensità si riducono al passare del tempo fino a decadere a zero come conseguenza dell’assorbimento delle pareti

2)      i tempi ai quali arriva un nuovo raggio si infittiscono sempre più a causa della crescita del numero di raggi riflessi.

Il fenomeno appena considerato è noto come riverberazione.

Con tale termine si intende dunque la persistenza del suono in un ambiente chiuso, dopo che la sorgente sonora ha cessato di irradiare, a causa della riflessione continuata del suono sulle pareti.

Il numero di riflessioni che nell’unità di tempo arrivano al ricevitore è definito come:

                                                                                                                           (3)         

Per dare un idea di come un’onda riflessa faccia ad arrivare dalla sorgente al ricevitore, basta applicare alcuni semplici concetti geometrici

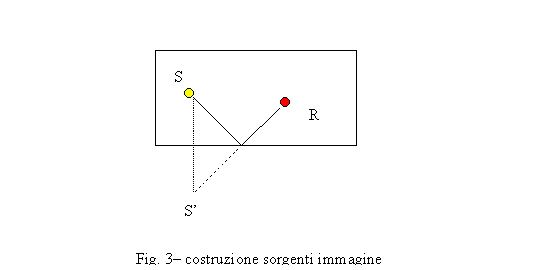
come detto in precedenza l’onda riflessa arriva al ricevitore con un certo ritardo rispetto all’onda diretta questo perché a causa della riflessione dovrà compiere una distanza maggiore.

È, dunque, come se provenisse da una sorgente immaginaria S’ posta al di fuori della stanza e avente distanza dalla sorgente maggiore rispetto a quella dell’onda diretta.

Se il raggio arriva dopo essere stato riflesso più volte avremo sorgenti immagine del secondo ordine, terzo ordine, quarto ordine e così via.

AMBIENTI RIVERBERANTI E SEMIRIVERBERANTI

Sostanzialmente possiamo dividere gli ambienti in due categorie, che si differenziano tra loro in base ad alcune proprietà.

Avremo:

  -         ambienti riverberanti

Gli ambienti riverberanti sono delle sale appositamente costruite che hanno un coefficiente di assorbimento nullo e sono munite di schermi atti a rendere uniforme la distribuzione del suono nell’ambiente.

Le pareti sono in grado di riflettere molto bene le onde sonore e quindi ad ogni riflessione le onde sonore subiscono perdite molto basse.

Queste riflessioni producono una distribuzione di energia acustica uniforme cosi che in ogni punto della sala si ha l’impressione che il suono arrivi da tutte le direzioni.

Normalmente sono camere di dimensioni non elevate e hanno la prerogativa di essere nn regolari.

Esse vengono utilizzate per la determinazione del coefficiente di riduzione del rumore, per controllare il rendimento di materiali e strutture, etc..

-         ambienti semiriverberanti

La maggior parte degli ambienti comuni sono di tipo semiriverberante.

A differenza degli ambienti riverberanti, gli ambienti semiriverberanti assorbono parte delle onde emesse dalla sorgente e di conseguenza si ha una perdita di energia.

PARAMETRI CARATTERISTICI DELL’AMBIENTE

Alcuni parametri caratteristici dell’ambiente, sono:

-         TR  = tempo di riverbero

-         Lm = libero cammino medio

-     ά coefficiente d’assorbimento medio dell’ambiente

Tempo di riverbero

Il tempo di riverbero nelle camere riverberanti è abbastanza alto, generalmente dell’ordine di 3-4 secondi.

Per misurare il tempo di riverbero ci sono due metodi:

1)      metodo che si basa sul regime stazionario interrotto

Supponiamo di porre una sorgente omnidirezionale all’interno di un ambiente.

Al tempo t = 0 accendiamo la sorgente e la lasciamo accesa per un certo intervallo di tempo in modo da saturare l’ambiente e successivamente la spegniamo bruscamente.

Se andiamo a costruire un diagramma dei livelli sonori in funzione del tempo, avremo una situazione del tipo:

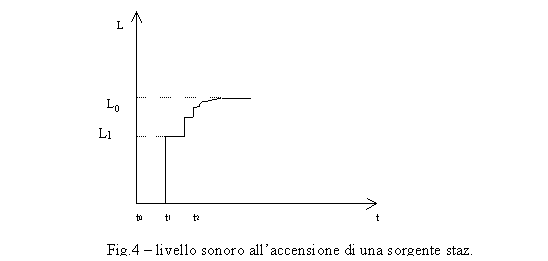
Al tempo t1 arriva il fronte diretto, che assume il valore L1.

A questo punto il livello rimane costante finchè al tempo t2 non arriva il suono prodotto dalla prima riflessione che va a sommarsi al suono dell’onda diretta cosi che il livello raggiunga il valore L2.

Come prima il livello rimane costante finchè al tempo t3 non arriva la seconda riflessione la quale fa salire di un gradino ancora l’intensità.

Via via che il tempo passa questi gradini diventano sempre più piccoli in quanto ad un suono forte si somma un suono sempre più debole e di conseguenza si raggiungerà un livello costante (che abbiamo identificato nel grafico con L0) che rappresenta la condizione di equilibrio energetico di un ambiente.

Nel momento in cui spegniamo la sorgente si verifica la situazione opposta.

Viene dapprima a mancare l’energia del suono diretto, però mentre questa all’atto di accensione aveva causato un brusco aumento del livello sonoro (in quanto si era passato dal silenzio totale al suono improvviso emanato dalla sorgente)adesso l’abbassamento che ne deriva è di entità molto modesta.

Ancora più modesto è l’abbassamento dovuto al primo raggio riflesso, cosi che dopo un primo tratto a gradini la curva tende a zero con un andamento rettilineo.

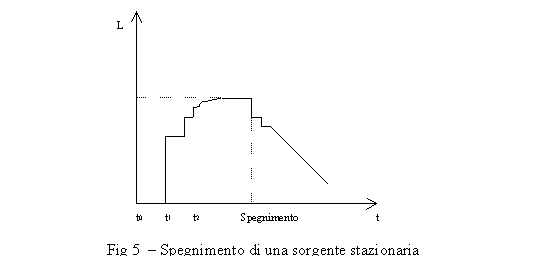
Nel momento in cui viene spenta la sorgente vi è un brusco calo del livello sonoro:

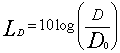                                                                                         (4)

D0 densità sonora.

Agli inizi del XX secolo W. Sabine definì il tempo di riverbero come il tempo necessario affinchè la pressione acustica nell’ambiente diminuisca di 60 dB, in seguito allo spegnimento della sorgente.

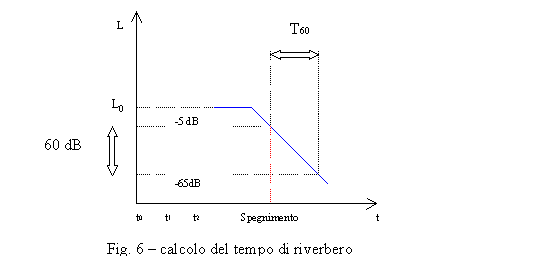
Viene indicato con il termine T60.

Seguendo le disposizioni della normativa si usa far partire il cronometro quando il livello è sceso di 5 dB, in modo da evitare il tratto scalinato, e si ferma quando è sceso di 65 dB complessivamente.

Rimane da fare una piccola considerazione.

Dal momento che 60 dB è un escursione abbastanza elevata spesso si considerano, per il calcolo del tempo di riverbero, intervalli minori i più comuni dei quali sono ad esempio 20 dB o 30 dB.

In questo modo avremo il T20 e il T30 .

Attenzione: il T20 (tempo che impiega il livello sonoro a decadere di 20 dB) non equivale ad 1/3 del T60 ma deriva da una estrapolazione fatta su una misura di 20 dB.

Il rapporto tra un tempo di riverbero e l’altro è del tipo:

                                                                                                 (5)

2) metodo della risposta dell’ambiente all’impulso

Si tratta di un metodo molto utilizzato data la sua semplicità e rapidità.

Consiste nel misurare l’uscita del sistema (la cosiddetta risposta impulsiva) in seguito ad una eccitazione impulsiva   

dove con d(t) si indica la funzione generalizzata impulso unitario, detto anche delta di Dirac, riproducibile approssimativamente mediante un colpo di pistola.

Noto l’impulso d’ingresso X(t) una volta analizzato il segnale d’uscita Y(t) possiamo ricavare la risposta dell’ambiente h(t) mediante l’integrazione all’indietro di Schroeder:

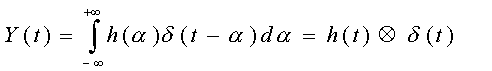      (6)

Spesso invece di utilizzare il delta di Dirac vengono utilizzati altri tipi di segnali, fra i quali vi sono:

-         Segnali MSL(Maximum Length Sequence)

Si tratta di una sequenza di tipo binario, come mostrato nel grafico sottostante:

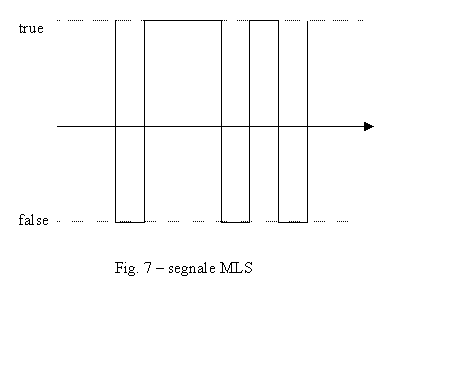
ottenibile con un software particolare che implementi uno shift register.

-         segnali Sine Sweep

Si tratta di un segnale con tono puro la cui frequenza varia con il tempo.

Sostanzialmente li possiamo dividere in due cartegorie:

-         lineare

-         logaritmico

quelli più utilizzati sono quelli di tipo logaritmico in quanto hanno la qualità di fornire più energia nelle regioni di bassa frequenza, che è una zona critica, e di procedere più velocemente nelle zone ad alta frequenza.

Tuttavia si presentano anche aspetti negativi dovuti alla potenza di calcolo che richiede.

Ritornando al tempo di riverbero è chiaro che questo è uno degli aspetti più importanti della progettazione acustica degli ambienti.

Infatti in base all’uso cui sarà adibito un ambiente vi sarà un certo tempo di riverbero, che sarà detto tempo di riverbero ottimo.

Nella tabella sottostante sono riportati i valori di tempo di riverbero ottimale per alcuni ambienti:

Grande importanza riveste anche il posizionamento degli altoparlanti in una stanza, a tal proposito introduciamo il concetto di distanza critica.

La distanza critica è quella distanza dalla sorgente alla quale il campo sonoro diretto assume lo steso valore del campo sonoro riverberante.

                                                                                                (7)

Se ci si trova entro la distanza critica dalla sorgente allora il suono diretto risulta chiaro e nitido a differenza del suono riverberante che risulta confuso.

In ambienti in cui bisogna prestare particolare attenzione a ciò che viene detto è bene dunque che l’ascoltatore venga posizionato entro la distanza critica. 

                                   fig 9 – altoparlante direttivo

L’altoparlante così posizionato è molto direttivo infatti il suono va a colpire direttamente le persone così che il suono è tutto diretto.

In una situazione del tipo:

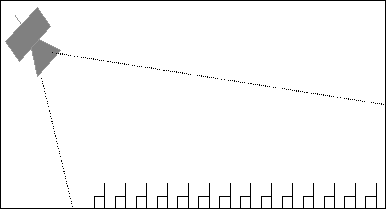
                                   fig. 10 – altoparlante poco direttivo

L’altoparlante risulta poco direttivo dando origine a forme di eco che sono causa di disturbo.

Un altoparlante poco direzionale può comunque essere utilizzato a patto che le pareti abbiano un alto coefficiente di assorbimento, per evitare il fenomeno suddetto.

Sintetizzando quanto detto finora, dal punto di vista ingegneristico ciò che ci interessa sapere è riuscire a quantificare il tempo di riverbero partendo dalle caratteristiche acustiche dell’ambiente.

Possiamo fare ciò servendoci della cosiddetta formula di Sabine:

                                                                                                      (7.1)

che esamineremo più avanti.                                                                                                                                                                  

Andamento della pressione al ricevitore

                    fig 11 – sorgente all’interno di un ambiente

Supponiamo di posizionare una sorgente all’interno dell’ambiente, la accendiamo e dopo un po’ di tempo il sistema andrà a regime e di conseguenza tanta energia viene fornita tanta ne viene assorbita dalle pareti.

Volendo fare un paragone con l’idraulica si potrebbe pensare ad un rubinetto che versa acqua in un contenitore.

Giunti a regime il livello che si stabilisce nel recipiente è tale che la portata d’acqua che entra è uguale a quella che ne esce.

                                           fig 12 – paragone con l’idraulica

Definiamo le seguenti grandezze:

                                                                                                              (8)                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

che mi fornisce il cammino che il raggio percorre tra due riflessioni consecutive;e

                                                                                                               (9)

che mi da il tempo medio  che intercorre tra due riflessioni.

Con:

S superficie totale dell’ambiente;

V volume dell’ambiente;

c velocità del suono.

L’espressione della conservazione d’energia può essere scritta come:

                                             dE = Es – Eα                                                            (10)

da cui l’energia del sistema è data da:

                                            Es = dE + Eα

Introduciamo adesso la grandezza densità di energia (indicata con D o con w) la cui unità di misura è :

In ogni intervallo di tempo infinitesimo dt vi è una frazione d’energia dE che colpisce le pareti e viene in parte riflessa in parte assorbita:

                                                                                                                            (11)

nell’istante di tempo tm l’energia incidente vale:

                                                                                                 (12)

per quanto concerne l’energia assorbita, questa vale:

dove:

                                                                                              (13)                                                                                                 

rappresenta il coefficiente di assorbimento medio, ossia la media dei coefficenti di assorbimento di tutte le pareti.

L’energia assorbita nel tempo dt risulta di conseguenza:

                                                                                  (14)

e andando a sostituire, in questa formula, a tm il valore trovato prima  =>

                                                                                  (15)

allora andando a sostituire nella Es = dE + Eα i valori appena trovati abbiamo che la potenza sarà:

                                                            ₍₁₆₎         

che è una relazione generale applicabile sia al caso stazionario che a quello variabile nel tempo.

Dopo un certo intervallo di tempo si raggiungerà la densità di regime data da:

                                                                                             (17)

da cui ponendo:

                                                                                               (18)

abbiamo che:

                                                                                   (19)

Quindi possiamo scrivere che:

                                                                                (20)

ma a noi interessa il livello di pressione in un ambiente riverberante, che sarà dato da:

                                                                                  (21)

Questa formula descrive solo in maniera molto approssimata quello che accade nella realtà.

Esiste però una versione che tiene conto sia dell’onda diretta che di quella riflessa.

Considerando la formula:

                                                                             (22)

con Q (direttività della sorgente).

Dalla somma algebrica delle due ultime equazioni otteniamo:

                                                                      (23)

che rappresenta l’equazione del campo semi-riverberante, comunemente utilizzata per determinare il campo sonoro dentro gli ambienti chiusi.

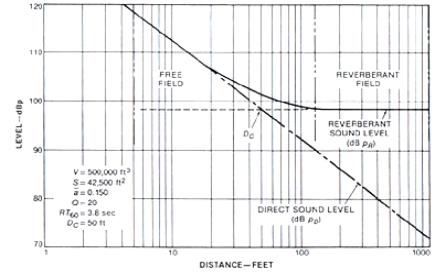
Nel grafico, di cui sopra, si riporta l’andamento del suono diretto e del campo riverberante.

Si nota come la sola presenza del suono diretto determini un decadimento perfettamente rettilineo (rappresentato dalla parte tratteggiata).

Calcolo del tempo di riverbero T60

Dalla formula trovata precedentemente (formula 16) che riscrivo per comodita:

si ricava che:

                                                                       (24)

da cui:

                                                                                            (25)

Siccome ragiono in termini di decrementi di energia dell’ordine di 60 :

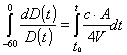                                                                                      (26)

da cui:

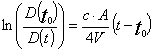                                                                               (27)

Per trovare il tempo t60, poniamo:  =>

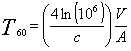                                                                                     (28)

e tenendo presente che 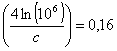   abbiamo che:

                                                                                                  (29)