Scambio termico per irraggiamento:
L’irraggiamento è il
terzo modo (dopo conduzione e convezione) in cui i corpi possono scambiare
calore. Esso si manifesta con il trasporto di energia
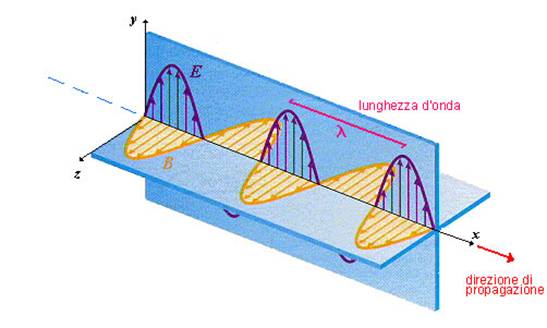
mediante onde elettromagnetiche, ossia onde che si propagano in direzione
rettilinea ed in cui campo elettrico E
e campo magnetico B oscillano in
piani ortogonali a se stessi ed alla direzione di propagazione.
|
|
Fig.1 – andamento del campo elettromagnetico.
La condizione di massimo
trasporto di energia si verifica quando i vettori E e B sono in fase tra di loro, quando si ha cioè quella che viene
definita “polarizzazione rettilinea”.
Nonostante alcune
somiglianze, campo acustico ed elettromagnetico presentano anche differenze fra di loro, la più visibile della quali è la posizione
reciproca fra la direzione di propagazione e le altre grandezze vettoriali che
caratterizzano l’onda: nel campo acustico avevano la stessa direzione, ora
invece sono poste su piani ortogonali. Inoltre, fino a qualche decennio
addietro, si credeva che mentre l’onda sonora necessitasse
di un mezzo in cui propagarsi (l’aria, ad esempio), l’onda elettromagnetica si
potesse propagare anche nel vuoto. In realtà anch’essa ha bisogno di un mezzo,
i fotoni: particelle elementari, definite come la quantità indivisibile di energia elettromagnetica. Quindi il trasporto di energia è quantizzato; questo fenomeno però, viste però
le elevate quantità di energia che analizzeremo, ci verrà mascherato, e potremo
sostanzialmente non preoccuparcene.
Dopo questa breve premessa,
suddividiamo ora le onde elettromagnetiche a seconda della
frequenza (e della lunghezza d’onda) da cui sono caratterizzate. Innanzitutto
ricordiamo la relazione che lega la frequenza f alla lunghezza d’onda l:
![]() (1)
(1)
dove
la costante c, pari alla velocità della luce, vale ![]() m/s.
m/s.
|
Tipo |
f (Hz) |
l (m) |
|
Onde hertziane |
|
|
|
Onde radio |
fino
a |
|
|
Microonde |
fino
a |
|
|
Infrarosso |
|
|
|
Luce visibile |
fino
a |
|
|
Ultravioletto |
|
|
|
Raggi X |
|
|
|
Raggi g |
|
|
|
|
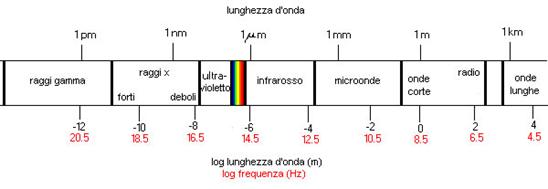
Fig.2 – spettro delle onde elettromagnetiche.
Le tre categorie di onde a più alta frequenza vengono dette “radiazioni
ionizzanti” e sono dannose per gli esseri viventi, in quanto le loro frequenza
è tale da mandare in risonanza gli elementi costituenti del corpo, spezzando i
legami molecolari e originando possibili mutazioni genetiche. Siccome
nell’analisi delle fonti di energia non bisogna scindere
gli effetti termici dai danni biologici che esse possono causare agli esseri
viventi, tali onde non verranno analizzate come possibili sorgenti
utilizzabili.
Per lo stesso motivo verranno trascurate le onde hertziane: i valori elevati di campo elettrico che le
caratterizzano sono in grado di provocare danni agli organismi viventi. Non
prenderemo neppure in esame le onde radio, essendo la loro innocuità ancora in
fase di studio.
La nostra attenzione,
quindi, si concentrerà soprattutto su microonde, infrarosso
e luce visibile.
Il corpo nero:
Occupiamoci
ora di studiare l’energia emessa da un corpo: solo per il fatto di trovarsi ad
una data temperatura, esso sarà sorgente di una radiazione elettromagnetica.
Alla
stessa temperatura, corpi diversi emanano energie distinte. Non è però
possibile che l’emissione superi un determinato valore; il “corpo nero” è la
sorgente in grado di raggiungere tale emissione limite
. Esso è un’astrazione matematica, il cui spettro è definito come l’inviluppo
delle radiazioni emesse da tutti gli altri corpi ad una data temperatura.
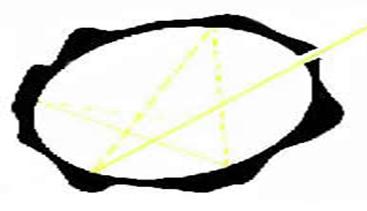
Nella realtà il corpo nero può essere approssimato con un corpo concavo, nero, non lucido,
scabro, in grado quindi di assorbire tutta la radiazione incidente, senza
rifletterla o trasmetterla.
|
|
Fig.3 – possibile realizzazione di un corpo nero: la radiazione che entra dal foro esce dal corpo solo dopo numerose riflessioni, nelle quali ha perso quasi tutta la sua energia.
Un corpo nero ha quindi
coefficiente di assorbimento a pari ad uno, e coefficiente di riflessione r nullo:
![]()
![]() (2)
(2)
dove Ia, Ir ed Ii sono rispettivamente le
intensità della radiazione assorbita, riflessa e incidente.
Leggi del corpo nero:
Le leggi che verranno ora
enunciate hanno validità ristretta al caso di corpo nero e non varranno, in
generale, per gli altri materiali.
Definiamo
innanzitutto il potere emissivo
integrale q: esso è pari alla potenza emessa per metro quadro di
superficie:
![]() (3)
(3)
dove E è l’energia emanata, t il tempo e S
la superficie. Dalla definizione si evince facilmente l’unità di misura di tale
potere emissivo integrale: W/m2.
La legge di Stefan-Boltzmann fornisce una relazione che lega q alla temperatura a cui il corpo è
posto:
![]() (4)
(4)
in cui il pedice 0 indica che ci stiamo riferendo al corpo nero. La costante s0, detta costante di Stefan-Boltzmann, vale:
![]() (5)
(5)
Per un corpo non nero, l’emissività integrale è inferiore a quella del corpo nero:
![]() (6)
(6)
Introduciamo ora un’altra grandezza: l’emissività e, definita come il rapporto fra l’emissività integrale di un corpo e quella
del corpo nero:
![]() (7)
(7)
tale rapporto è ovviamente pari a 1 solo nel caso di
corpo nero.
Passiamo
ora a definire il potere emissivo
monocromatico q¢, cioè la quantità di
energia emessa per intervallo di lunghezza d’onda:
![]() (8)
(8)
da cui si ricava:
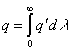 (9)
(9)
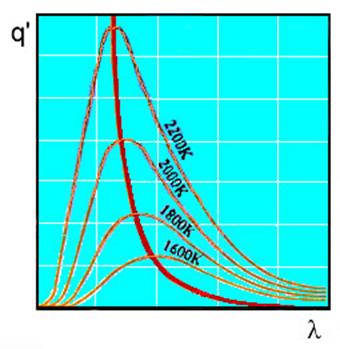
Definiamo infine l’emissività monocromatica
e¢ come:
![]() (10)
(10)
|
|
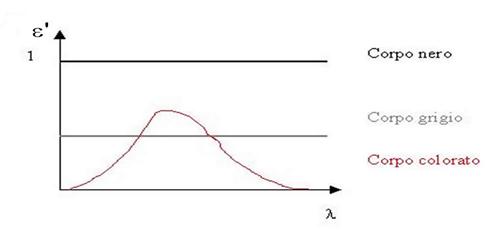
Fig.4 – andamento
dell’emissività monocromatica per corpi neri, grigi e colorati.
Un corpo grigio è un corpo il cui coefficiente di assorbimento
è costante, seppur minore di uno. Quindi l’emissività
monocromatica è minore di 1, ma, come per il corpo nero, essa rimane costante
con la lunghezza d’onda.
E’
quindi possibile riformulare la legge di Stefan-Boltzmann per il corpo grigio:
![]() (11)
(11)
Legge di Wien (o del regresso):
Dall’analisi dello
spettro di emissione di un corpo nero si nota come,
con l’aumento della temperatura, esso raggiunga un valore di picco massimo
sempre più elevato, la cui lunghezza d’onda corrispondente è sempre minore.
La legge di Wien enuncia che la temperatura alla quale il corpo è
sottoposto e la lunghezza d’onda alla quale corrisponde l’emissività massima sono inversamente proporzionali:
![]() (12)
(12)
|
|
Fig.5 – i punti di massima emissività giacciono su
un’iperbole equilatera.
Legge di Planck:
La legge di Planck
esprime l’andamento dell’emissività in funzione della temperatura a cui il
corpo è sottoposto e della lunghezza d’onda:
![]() (13)
(13)
dove le due costanti valgono:
![]()
![]() (14)
(14)
Quando la
temperatura T è così elevata che il
corpo risulta incandescente, il picco diventa marcatissimo:
|
|
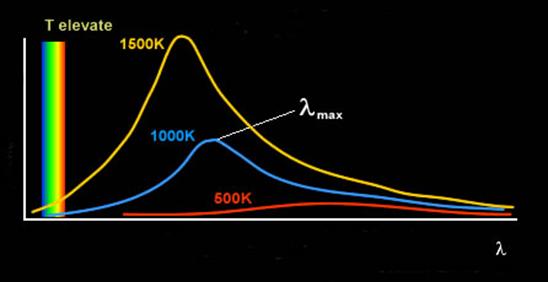
Fig.6 – a temperature elevate il picco di massima
emissione risulta marcatissimo e il corpo emette luce
Come già detto, al
crescere della temperatura, il punto di massimo si sposta
verso lunghezze d’onda basse, spostandosi dall’infrarosso al visibile: per
questo motivo i corpi, scaldandosi, tendono ad emettere luce visibile. Tale
punto di massimo viene detto temperatura
di colore. Vediamo alcuni esempi di sorgenti luminose e relative
temperature di colore:
· lampadine a incandescenza: 3500 K;
· tubi fluorescenti: 7000 K;
·
lampada allo
Xenon: 5500 K (prossima a quella del Sole).
Paradossalmente, per la
nostra percezione, le luci cosiddette “calde” (quali quelle rosse) hanno una
temperatura di colore inferiore a quelle che consideriamo “fredde” (quali
quelle blu). Il concetto di temperatura di colore acquista notevole importanza
in fotografia, ove le pellicole vengono progettate in
modo da compensare eventuali eccessi di luce rossa o azzura. Al contrario, le
moderne telecamere (come d’altronde l’occhio umano) sono in grado di effettuare automaticamente questa compensazione.
Legge di Prevost:
Tale legge enuncia che il
bilancio netto di energia, ossia la quantità di calore scambiato qs, è pari alla differenza
fra il calore emesso qem
e quello ricevuto qric:
![]() (15)
(15)
dove
si è sfruttata la relazione fra quantità di calore ricevuto qric, coefficiente di
assorbimento a ed quantità di calore
incidente qinc.
Ovviamente tale
legge ha carattere generale.
Legge di Lambert:
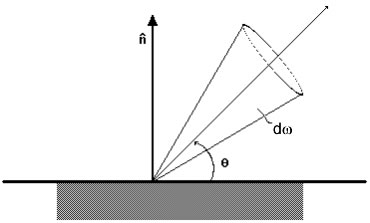
Definiamo per prima cosa
il potere emissivo angolare i: esso
è pari al rapporto tra la quantità di energia fluente
attraverso l’angolo solido di ampiezza dw e l’angolo solido stesso
![]() (16)
(16)
|
|
Fig.7 – determinazione del potere emissivo
angolare.
Da ciò si ricava banalmente:
![]() (17)
(17)
La legge di Lambert
afferma che l’intensità di emissione iq in una
data direzione è pari al prodotto fra l’intensità in direzione normale alla
superficie emettente e il coseno dell’angolo compreso fra le due direzioni:
![]() (18)
(18)
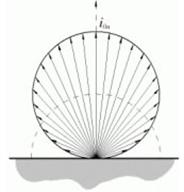
L’inviluppo
delle ampiezze del potere emissivo angolare è una circonferenza:
|
|
Fig.8 – andamento spaziale del potere
emissivo angolare.
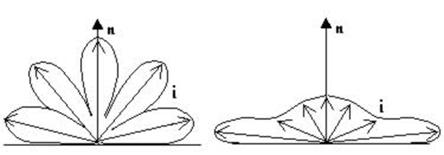
Altri corpi invece non
seguono questa legge, assumendo così inviluppi bizzarri:
|
|
Fig.9 – andamento spaziale del potere emissivo
angolare.
Rispetto ad una ipotetica emissione uniforme,
spesso utilizzata per rappresentare l’emissione di corpi non neri (a semisfera)
il valore in direzione normale dell’emissione di Lambert deve essere doppio di
quella uniforme a parità di potere emissivo integrale.
![]() (19)
(19)