Tecniche di misura avanzate della risposta all’impulso

Le tecniche di misura di risposta all’impulso avanzate, che affronteremo da qui in avanti, si basano su misurazioni elettroacustiche. Vedremo e analizzeremo la generazione di un segnale di eccitazione artificiale (prodotto nel nostro caso dal computer), immesso nell’ambiente circostante (l’aula) da un impianto di riproduzione e la deconvoluzione della risposta all’impulso a partire dalla risposta dell’ambiente all’eccitazione misurata attraverso un microfono. Prima di procedere in questo senso è però utile riprendere la teoria dei sistemi lineari tempo invarianti (abbreviazione SLI).

Convoluzione analogica e digitale

Dal punto di vista matematico, un sistema è una trasformazione che ad un segnale d’ingresso x(t) fa corrispondere un ben determinato ed unico segnale d’uscita y(t).

Il teorema della convoluzione afferma che la risposta h(t) di un segnale è univocamente determinata dalla relazione matematica che lega il segnale d’ingresso x(t) al segnale d’uscita y(t).

(1)

La formula (1) esprime la cosiddetta convoluzione analogica, nella quale il simbolo viene identificato come l’operatore di convoluzione.

Quando passiamo da un sistema continuo ad un sistema discreto costituito da segnali campionati (come ad esempio all’interno di un computer) abbiamo che il tempo corrente è dato dalla relazione

(2)

Campionare un segnale x(t) significa “estrarre” dal segnale stesso i valori che esso assume ad istanti temporali equispaziati, cioè multipli di un intervallo detto appunto periodo di campionamento (nell’esempio di un computer, esso è caratteristico della scheda audio).

Il segnale campionato in uscita è allora dato da

(3)

In questa relazione, che rappresenta la cosiddetta convoluzione digitale o discreta, N indica il numero di campioni che rappresentano la risposta all’impulso.

Dopo aver analizzato la convoluzione nel dominio del tempo affrontiamo ora quella nel dominio della frequenza.

L’algoritmo di FFT

Risulta a questo punto opportuno introdurre il concetto di FFT (Fast Fourier Transform), un algoritmo veloce di calcolo della trasformata discreta di un segnale, che riduce la complessità computazionale dell’algoritmo stesso e che, a parità di frequenza di clock dell’elaboratore, permette l’utilizzo di frequenze di campionamento elevate.

L’algoritmo di FFT fu pubblicato nel 1965 da Cooley e Tukey; a questa data si fa risalire la nascita della moderna elaborazione numerica dei segnali.

Attraverso la FFT, infatti, possono essere effettuate in maniera efficiente alcune operazioni fondamentali di analisi ed elaborazione dei segnali (analisi spettrale e filtraggio). Tali operazioni non furono realizzabili in pratica fino al momento dell’introduzione dell’algoritmo veloce, vista la ridotta velocità dei componenti elettronici e quindi dei calcolatori dell’epoca.

Se applico ora l’analisi di Fourier ai segnali x ed y ed alla risposta impulsiva h ottengo

dove X(w), Y(w) ed H(w) sono le trasformate di Fourier nel dominio della frequenza.

Da queste considerazioni si ottiene pertanto l’importante relazione

(4)

La convoluzione nel tempo può essere implementata attraverso l’inversa della FFT

(5)

Supponiamo adesso di voler determinare la risposta all’impulso di un ambiente (ad esempio l’aula), una volta generato il segnale x (attraverso il computer) e conosciuto e misurato (attraverso un microfono) il segnale y.

Dalla (4) nel dominio della frequenza ricavo

(6)

e facendo l’analogo di quello che avevamo fatto nella (5) otteniamo

(7)

Questa relazione è valida indipendentemente dal tipo di segnale introdotto in ingresso (es. rumore bianco, rumore rosa, sinusoide sweepata, musica...), purché lo spettro di energia del segnale x stesso copra tutte le frequenze, altrimenti in certi casi potrei trovarmi uno 0 al denominatore nella (7).

È dunque opportuno scegliere un segnale che vari su tutto l’asse delle frequenze, in modo che le sue statistiche non siano così “sballate” da far aumentare notevolmente il tempo necessario per la misura del segnale stesso.

Time aliasing

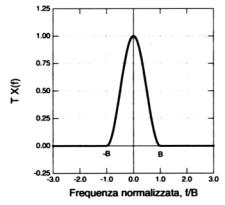
Figura 2 – Segnale analogico a banda limitata

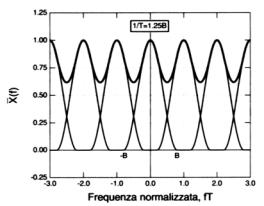
Figura 3 – Sovrapposizione delle repliche dovuta al fenomeno di aliasing

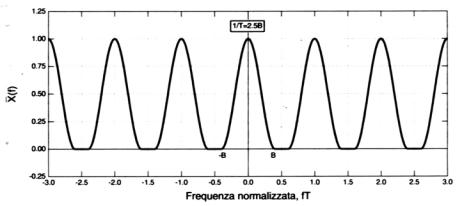
Figura 4 – Sequenza non soggetta al fenomeno di aliasing

Preso un segnale x(t) a banda limitata come lo spettro mostrato in Figura 2 possiamo vedere l’effetto provocato dalla scelta di due differenti frequenze di campionamento f_c. Nella Figura 3 la frequenza di campionamento è tale che le varie repliche della trasformata di x(t) centrate sui multipli della f_c e derivanti dalla periodicizzazione dello spettro vengono a sovrapporsi. Nella Figura 4, invece, la frequenza di campionamento è sufficientemente alta e non si ha sovrapposizione. Nel primo caso, dunque, le varie repliche dello spettro “interferiscono” sommandosi alla replica base e producendo un errore di aliasing, che porta ad una distorsione del segnale.

La maggioranza degli analizzatori FFT svolgono l’algoritmo con un massimo di 4096 punti (o campioni) e poiché il tempo di realizzazione cresce con N², per un numero elevato di campioni l’FFT diventa molto pesante.

Il segnale MLS

Un matematico tedesco, Alrutz, ovviò a questo inconveniente sviluppando una nuova tecnica detta MLS (Maximum Length Sequence), una sequenza binaria, costituita cioè da due soli valori estremi della forma d’onda (Figura 5).

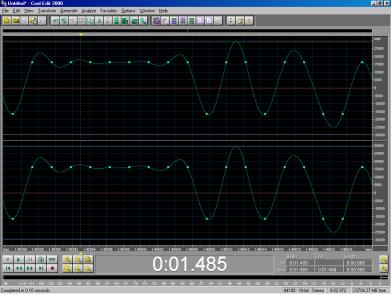
Figura 5 – Valori estremi della forma d’onda di un segnale MLS

Questo segnale ha uno spettro piatto in banda della frequenza e “suona” come un rumore bianco (Figura 6); esso viene generato con un operatore logico chiamato SHIFT REGISTER (registro di scorrimento), costituito da un certo numero di celle, inizializzate ciascuna con un valore opportuno, che può essere 0 oppure1. Ad ogni passo ogni campione viene comunicato alla cella successiva; alla fine esce un valore e l’ingresso viene rialimentato con un operatore logico (che può essere AND oppure OR) fra una opportuna cella intermedia e l’uscita.

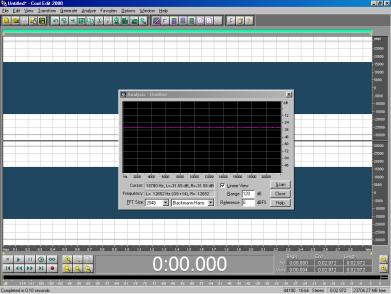
Figura 6 – Rumore bianco analizzato con Cool Edit 2000

Una particolarità del segnale MLS è che correlandolo con se stesso (quella che matematicamente si chiama autocorrelazione) il risultato è un impulso ideale o d di Dirac.

(8)

dove indica l’operatore di crosscorrelazione (ed in questo caso specifico di autocorrelazione).

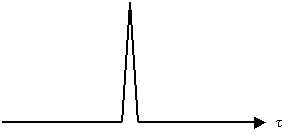
La tecnica di misura della risposta all’impulso h con l’MLS non richiede l’utilizzo dell’algoritmo di FFT; infatti, la crosscorrelazione eseguita nel tempo tra il segnale MLS generato (x) ed il campione in uscita (y) produce la risposta cercata (h).

(9)

e grazie alla (8) otteniamo

(10)

L’operazione di crosscorrelazione viene risolta in maniera ottimale con l’algoritmo detto FAST HADAMARD TRANSFORM (algoritmo equivalente all’FFT ma specifico per il segnale binario preso in considerazione).

Descrizione dell’esperimento

Prima di vedere alcuni dei risultati conseguiti attraverso l’esperienza svolta a lezione, analizziamo la Figura 8, che riproduce uno schema semplificato di un sistema di registrazione di un segnale acustico su Compact-Disc (CD).

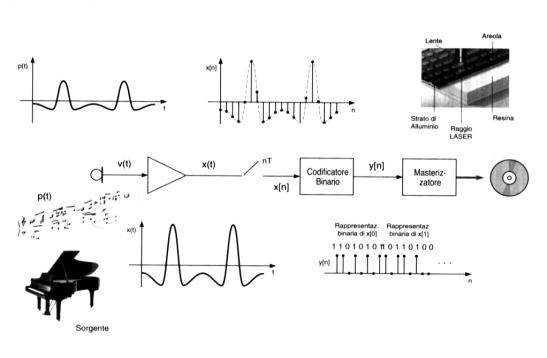
Figura 8 – Schema di un sistema di registrazione su CD Audio

Il segnale utile che deve essere registrato è la variazione di pressione acustica p(t) prodotta dalla sorgente del segnale stesso (in questo caso il pianoforte). Tale segnale viene convertito in una debole tensione elettrica v(t) dal microfono, che svolge la funzione di trasduttore, cioè di dispositivo che cambia la natura del segnale mantenendone inalterata la forma. La tensione prodotta dal microfono deve essere amplificata prima di poter essere ulteriormente elaborata, ottenendo così la nuova tensione x(t).

Tutti i segnali considerati finora sono analogici; poiché, però, si desidera registrare il segnale con componenti e circuiti digitali, la forma d’onda x(t) viene allora campionata, ottenendo la sequenza x[n] dei valori di x(t) considerati ai multipli di un opportuno periodo di campionamento T : x[n] = x(nT).

Il segnale è stato adesso ridotto a tempo discreto, ma i vari campioni di x[n] assumono ancora infiniti valori nell’insieme dei reali. Si deve quindi procedere ad un’ulteriore codifica di questi valori reali attraverso l’alfabeto binario tipico dei circuiti digitali, per ottenere il segnale digitale binario y[n]. Nell’esempio della registrazione su CD, il campionamento del segnale avviene alla cadenza standardizzata di 44100 campioni/secondo e la codifica binaria dei valori reali del segnale campionato è in virgola fissa su 16 bit.

L’unione delle operazioni di campionamento e codifica prende il nome di conversione analogico/digitale e viene realizzata da appositi circuiti elettronici detti appunto convertitori A/D. Il segnale digitale binario y[n] viene quindi registrato sul CD dal cosiddetto masterizzatore; i valori delle cifre binarie di y[n] che si susseguono nel tempo vengono registrati sotto forma di areole riflettenti o assorbenti la luce (a seconda del valore 0 o 1) lungo un “solco” a spirale che si svolge dal centro verso la periferia del CD stesso. Questo segnale sarà poi riletto dal laser dell’apparecchio lettore, riconvertito in segnale analogico, amplificato e inviato ad un altoparlante per ricostruire con la massima fedeltà il segnale-messaggio originario p(t).

Passiamo ora ad analizzare l’esperienza svolta in aula. Come detto in precedenza, nello svolgimento di questa abbiamo utilizzato un sistema di registrazione ed elaborazione, un impianto di riproduzione ed un microfono SOUNDFIELD. Quest’ultimo è costituito da 4 capsule microfoniche montate idealmente ai quattro vertici di un tetraedro ed il segnale che esce dal microfono ha 4 canali: il segnale di pressione sonora w e le tre componenti cartesiane della velocità x, y e z.

Figura 9 – Il microfono Sounfield

Come segnali di “eccitazione” in ingresso si sono utilizzati il segnale MLS e lo SWEEP. Lo SWEEP, che può essere di due tipi, lineare o logaritmico, è un segnale composto da un tono puro la cui frequenza aumenta nel tempo con un determinato andamento (Figura 10 e Figura 11).

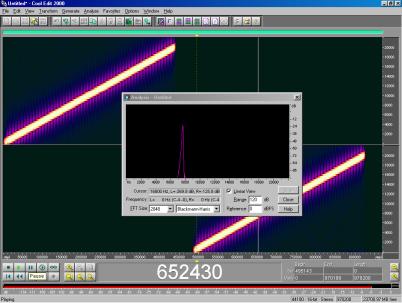
Figura 10 – Analisi di uno SWEEP lineare

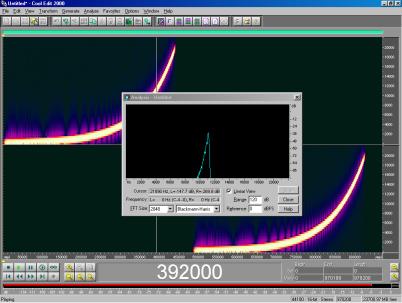
Figura 11 - Analisi di uno SWEEP logaritmico

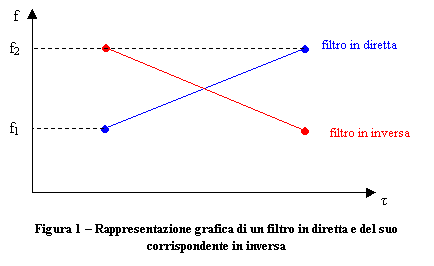
Verso la metà degli anni ’80 una nuova tecnica soppiantò la vecchia teoria MLS e venne in seguito identificata con la sigla TDS (Time Delay Spectrometry); questa venne da subito utilizzata in misure di tipo ottico e nella propagazione delle onde radio. Nella TDS si usa una sinusoide con sweepaggio lineare, la cui frequenza varia linearmente nel tempo da un valore f₁ iniziale ad un valore f₂ finale; lo spettro di un segnale sweepato linearmente è uguale a quello di un rumore bianco.

La misura tradizionale TDS veniva fatta mediante il segnale proveniente dal microfono che a sua volta veniva messo in ingresso ad un filtro inseguitore (filtro passa-banda, che “lascia passare” un campo di frequenze molto stretto): se i segnali d’entrata e d’uscita erano sincronizzati, allora il segnale che emergeva dal filtro era il suono diretto.

Recentemente si è giunti ad una soluzione più semplice per determinare la risposta all’impulso h(t). Riprendendo il sistema di partenza di Figura 1 (con in ingresso uno SWEEP lineare), esiste, allora, un filtro inverso x'(t) tale che

(11)

produce la risposta h(t) cercata. Ciò è vero se vale la relazione

(12)

Da quanto detto in precedenza, il filtro inverso cercato non è altro che la sweepata lineare stessa rovesciata sull’asse dei tempi.