Alcune definizioni
Legge di Dalton
Equazione di stato
Esempio dell'aria
Miscele Nitrox
Entalpia specifica
Titolo improprio o umidità assoluta
Umidità relativa
1.1 Premessa
La base per lo studio delle miscele di aeriformi è indubbiamente costituita dalla legge di Dalton.
Per descrivere il comportamento di un miscuglio è indispensabile conoscerne la composizione e un determinato numero di proprietà fisiche, che vanno determinate sperimentalmente.
Se, però, si tiene conto del gran numero di miscele da considerare, risulta chiaro il vantaggio offerto dalla possibilità di caratterizzare il miscuglio partendo dalla conoscenza delle proprietà dei suoi singoli componenti.
Questo particolare approccio fornisce buoni risultati quando è possibile ammettere che i componenti del miscuglio si comportino come gas ideali. Nel caso di gas reali, infatti,è preferibile ricorrere a diagrammi termodinamici forniti dallo studio diretto della miscela.
Come esempio, in figura 1.1 è riportato il diagramma entropico dell' aria, nella zona in cui il suo comportamento va ricondotto a quello di gas reale.
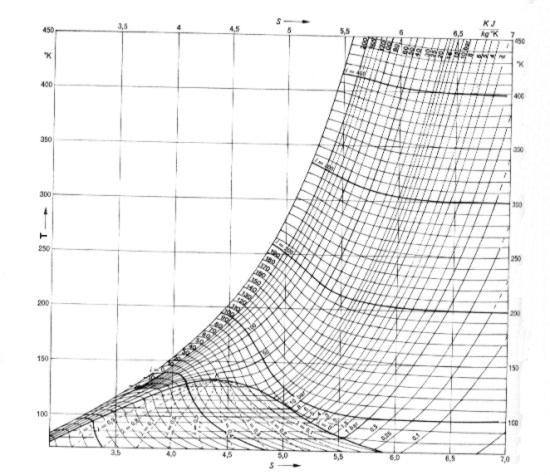
Fig. 1.1 - Diagramma entropico dell' aria.
S = entropia [kJ/kg °C] T = temperatura[°K]
i = entalpia[kJ/kg] p = pressione[bar]
1.2 Miscele di gas ideali
Premettiamo alcune definizioni e relazioni utili:
Con N indicheremo il numero dei componenti del miscuglio. Se ni è il numero di moli del componente i-esimo e n quello totale, per definizione si ha che :
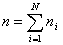
Se Mi è la massa del componente i-esimo e MTOT quella del miscuglio, risulta
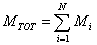
grazie al fatto che la massa gode della proprietà additiva.
Siano, inoltre, T e V la temperatura e il volume occupato dalla miscela di gas che si possano considerare ideali; si definisce pressione parziale del componente i-esimo quella che ni moli di esso eserciterebbero se occupassero da sole, alla temperatura T, tutto il volume V della miscela.
Come anticipato nella premessa, la legge di Dalton (dal nome del suo scopritore John Dalton) è fondamentale nello studio delle miscele di gas.
Essa afferma che :
"La pressione totale di una miscela è la somma delle pressioni parziali dei singoli gas che la compongono".
In formula:
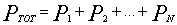
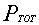= pressione del sistema
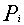= pressione parziale del componente i-esimoQuesta legge si riferisce a gas sufficientemente rarefatti, il cui comportamento è assimilabile a quello dei gas perfetti.
Essa consente di lavorare secondo il cosiddetto principio di sovrapposizione degli effetti.
In particolare, caratterizza l'additività delle pressioni parziali.
Risulta, inoltre, da questa legge, che ciascun componente si comporta sempre, in una miscela di gas ideali, come se si trovasse da solo, alla temperatura T, occupando il volume V del miscuglio, ed alla pressione parziale Pi.
Fra i gas della miscela non vi è, quindi, interazione.
Le cose cambiano in presenza di un gas non perfetto: non c'è più una situazione simmetrica, solo il gas perfetto, cioè, rimane indipendente dagli altri.
Per ciascun componente, scriviamo l' equazione di stato dei gas perfetti:
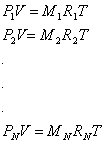
sommo queste equazioni membro a membro e ottengo la relazione:
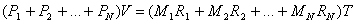
che riscrivo come
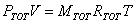
dove RTOT, indicata anche con R', è la costante R del miscuglio ed è una media pesata delle constanti R dei gas che lo costituiscono. Infatti:
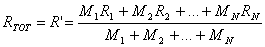
Con buona approssimazione, possiamo considerare l'aria una miscela di gas perfetti, costituita da ossigeno (O2) e azoto (N2), le cui percentuali volumetriche sono, rispettivamente, 0.7809 e 0.2095.
La legge di Dalton, per l' aria, diventa
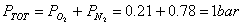
Ricaviamo ora la costante R' dell'aria.
Riscrviamo la formula:
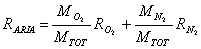
Mi occorre calcolare le costanti dell'ossigeno e dell'azoto. I rispettivi pesi molecolari sono:
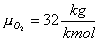e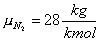 
quindi
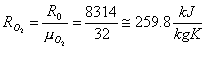
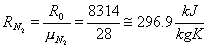
Calcolo le frazioni in massa dei due componenti.
Ricordiamo che la frazione in massa del componente i-esimo, indicata con gi, è data dalla formula:
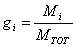
Per ognuno dei due gas scriviamo le equazioni dei gas perfetti in forma molecolare:
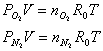
divido membro a membro:
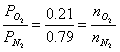
il rapporto tra la massa dell'O2 e dell'N2 è dato da
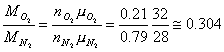
suppongo che
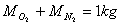
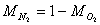
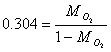
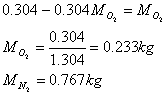
Si noti che le frazioni in massa sono in generale diverse da quelle in volume.
Abbiamo ricavato tutto quello che ci occorre per calcolare la costante R' dell'aria:
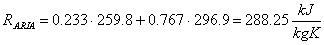
Il suo valore sperimentale è, però, leggermente diverso; infatti
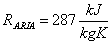
Ciò è dovuto al fatto di aver considerato l' aria un miscuglio di gas perfetti; è chiaro, comunque, che questa approssimazione ci ha fornito buoni risultati.
Una miscela costituita da O2 e N2 in percentuali non standard, ossia diverse da quelle che caratterizzano l' aria, è detta Nitox.
Si tratta, in genere, di miscugli con una percentuale di O2 maggiore di quella dell' aria, soprattutto perché è molto difficile sottrarre ossigeno ad una miscela, in quanto miscelare due gas costituisce una trasformazione irreversibile.
1.3 Esercizio - scatolone adiabatico
Si supponga che in un recipiente rigido, con pareti perfettamente adiabatiche, si trovino ossigeno e azoto, divisi da un diaframma, alla pressione e alla temperatura assegnate.
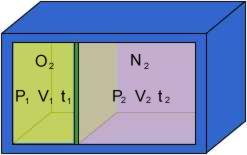
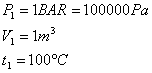
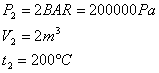
Togliendo il diaframma, i due gas si miscelano e, dopo un certo tempo, la miscela risulta fisicamente omogenea.
.:: Calcolare il volume (V3), la massa (M3), la temperatura(t3) e la pressione(P3) del miscuglio.
.:: Determinare la composizione del NITROX (in massa e in volume).
.:: Calcolare la variazione di entropia del sistema.
Risoluzione
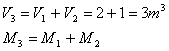
Le masse M1 e M2 possono essere ricavate dall'equazione dei gas perfetti
quindi
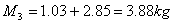
Ricaviamo la temperatura del miscuglio dall'espressione della sua energia interna:
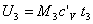
dove c'V è una media pesata delle costanti termiche cV1 e cV2 dei componenti della miscela, ossia:
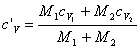
Poichè sia il lavoro compiuto che il calore scambiato sono nulli, tale è anche la variazione dell'energia interna:
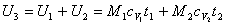
Per calcolare cV1 e cV2, sfrutto le due note relazioni:
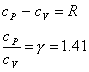
Per quanto riguarda l'O2:
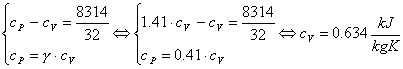
Con un procedimento del tutto analogo, calcoliamo la cV per l'azoto.
Dunque
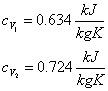
Abbiamo tutti i dati per calcolare l'energia interna della miscela (U3) e la sua costante termica a volume costante
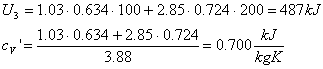
Infine, determiniamo la temperatura t3
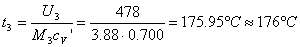
L'ultima grandezza da calcolare è la pressione P3.
Anche per il miscuglio finale posso scrivere l'equazione dei gas perfetti:
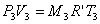
da questa ricaviamo P3, dopo aver calcolato la costante R'
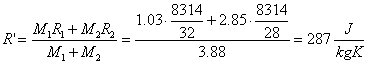
Dunque
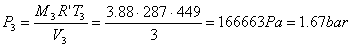
Determiniamo le percentuali in massa (o ponderali) della miscela. Si indicano generalmente con la lettera g.
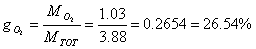
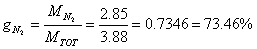
Calcoliamo, infine, le percentuali in volume (o molari). Si indicano con x. In generale
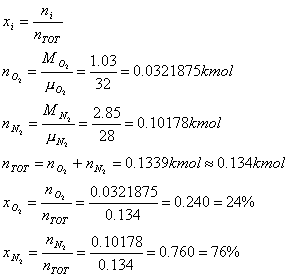
Per quanto riguarda l' entropia del nostro sistema, è intuitivo concludere che, durante l' operazione di miscela considerata, si produce una variazione positiva di entropia, comunemente detta "entropia di mescolamento".
Sappiamo che, per una generica trasformazione da uno stadio a ad uno stadio b, la variazione di entropia di un singolo gas in una miscela di gas ideali può essere determinata dalla formula :
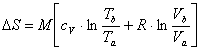
Nel caso del nostro esercizio:
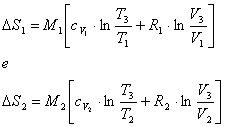
E' importante notare come nelle due formule sia presente il volume finale V3.
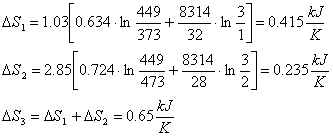
2.1 Premessa
Con il termine vapore si indica uno stato gassoso vicino alla regione di saturazione e si evidenzia la possibilità di una condensazione dovuta ad una trasformazione.
Le miscele d' aria e vapore d' acqua sono quelle che rivestono un' importanza pratica maggiore.
Sono, infatti, legate a problemi connessi direttamente alla vita dell' uomo, agli eventi meteorologici o a diffusi problemi tecnici.
In questa lezione verranno trattate esclusivamente le miscele d' aria e vapore d' acqua, ma i risultati raggiunti hanno validità generale e possono essere riferiti ad un qualsiasi miscuglio comprendente uno o più gas e un vapore.
2.2 Miscele d'aria e vapore d'acqua
L'aria atmosferica, oltre ad ossigeno, azoto e piccole quantità di altri gas, contiene anche vapor d' acqua.
Quando non contiene vapore, l'aria viene definita "secca".
Nel caso dell' aria atmosferica, è possibile considerare l' insieme come una miscela a due componenti, aria secca e vapore d' acqua.
In molte applicazioni, la pressione parziale del vapore (PV) è inferiore alla sua pressione di saturazione (PVMAX o PSAT(T)) e la temperatura dell' aria varia tra circa -10°C e circa 50°C.
In questo campo di variazione, sia l' aria secca, che il vapore d' acqua, possono essere trattati come gas perfetti, con una perdita di precisione trascurabile (inferiore allo 0.2 per cento).
Ad ogni modo, si continua a considerare il vapore un gas ideale anche quando questo è vicino alla saturazione, grazie alla quantità relativamente piccola in cui è presente nell' aria (meno dell' 1 per cento a 20/25 °C).
L' aria atmosferica, quindi, può essere trattata come un miscuglio di gas perfetti.
2.3 Grandezze specifiche improprie
In generale, si definisce entalpia specifica (h') il rapporto:
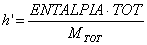
Nel caso dell'aria atmosferica (umida), si esprime, invece, con riferimento all'unità di aria secca e non all'unità di aria umida:
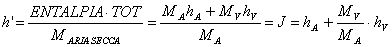
Si definisce titolo improprio o umidità assoluta (indicata con x o y) la quantità di vapore d'acqua effettivamente presente in 1kg di aria secca:
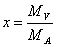
nota: spesso si confonde l'umidità assoluta con il titolo (x) riferito alle miscele sature:
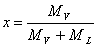
ML = massa del liquido
che può assumere valori compresi tra 0 e 1.
Si definisce grado igrometrico o rapporto di umidità relativa (UR) il rapporto tra la quantità effettiva di vapore d' acqua contenuta nell' aria e il massimo quantitativo che l' aria può contenere ad una data temperatura.
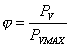
dove PV è la pressione parziale del vapore d'acqua e PVMAX la sua pressione di saturazione.
L'umidità relativa varia fra 0 (aria secca) e 1 (aria satura).
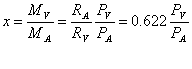
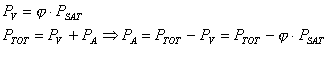
Possiamo, quindi, esprimere il titolo come:
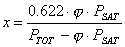
e l'umidità relativa come:
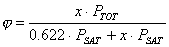
Sapendo che
, 
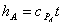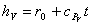
dove r0 è il calore latente di vaporizzazione
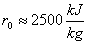
riscriviamo l'espressione dell'entalpia specifica (Mollier)
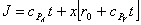
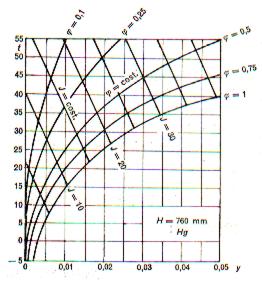
Gli stati delle miscele aria- vapor d' acqua sono in genere riportati su diagrammi in cui, considerata costante la pressione, una delle variabili è, in ogni caso, il titolo dell' aria umida (y); l'altra, l' entalpia o la temperatura.
Nella figura 2.1 è riportato schematicamente un diagramma ortogonale (t, y).
