Antonio Notaro  n .matricola:130901

Lezione del 15/10/2001

Ore 16.30-18.30

 

 

ENTALPIA & ENTROPIA

 

DEFINIZIONE : VARIABILE DI STATO

Si definisce variabile di stato la grandezza di un sistema termodinamico che dipende dal suo stato iniziale e finale ma non dal cammino termico seguito.

 

MATEMETICAMENTE:Definita s come una variabile arbitraria di stato ,su un percorso

                                          qualsiasi che va da uno stato di equilibrio ad un altro si deve

                                          verificare la condizione:

                                        

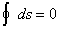
ENERGIA INTERNA

Il primo principio della termodinamica dice che la variazione di energia interna ”E” di un sistema dipende dal lavoro “L” fatto su di esso e dalla quantità di calore “Q” da esso      scambiata con l’esterno:E=Q-L

Inoltre il primo principio afferma che:”In ogni trasformazione termodinamica tra due stati di equilibrio la quantità  Q-L mantiene lo stesso valore fra lo stato iniziale e lo stato finale indipendentemente dal percorso termodinamico seguito”.Quindi l’energia interna e’ una variabile di stato !

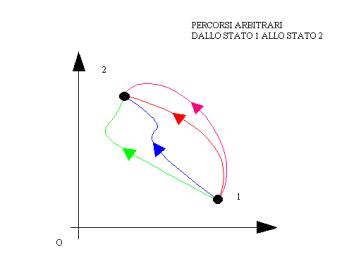
Si consideri ora una trasformazione isocora di un gas ideale:

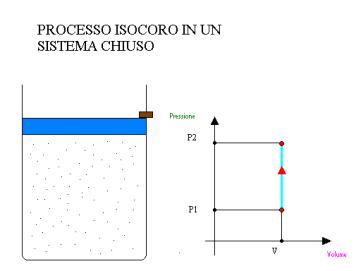
il lavoro che il gas svolge sull’esterno e’ nullo poiché il  pistone e’ bloccato da un perno(quindi non si ha spostamento).La variazione di energia interna quindi e’ pari al solo calore scambiato con l’ambiente esterno:E =Q . Il calore scambiato e’ legato alla temperatura dalla relazione:Q =M C v (T2 –T1) dalla quale ricaviamo che E =M C v(T2-T1).

OSSERVAZIONI:

1.               Il risultato, anche se ottenuto per una particolare trasformazione, può essere generalizzato .

2.               La variazione di energia interna può essere intesa come il calore scambiato dal sistema in una trasformazione isocora.

3.               Il risultato esplicita il ruolo dell’energia interna come variabile di stato :le due temperature che compaiono nella formula non dipendono dal percorso termico seguito durante la trasformazione ma dallo stato di partenza e da quello d’arrivo.

 

 

ENTALPIA

Si consideri una trasformazione isobara di un gas ideale:

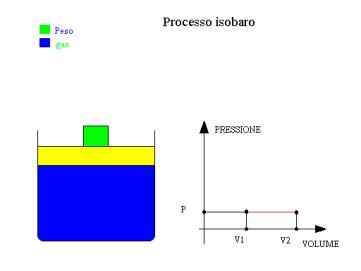
dal primo principio si ricava che Q =E + p*V . Si definisca quindi una nuova grandezza :H =E + P * V allora per il processo isobaro avremo:Q =H2-H1.

La grandezza così definita e’ detta ENTALPIA.

Applichiamo il primo principio della termodinamica alla trasformazione isobara:E =Q- L =Q- P * (V2-V1). Isolando la quantità di calore dall’ultima equazione si ottiene:( E2+P2*V2)-(E1+P1*V1) =Q ossia H2-H1=Q .Osserviamo adesso che il calore scambiato dipende linearmente dalla temperatura:Q =M C p (T2-T1) dove M e’ la massa del gas, C p la capacità termica a pressione costante e T2, T1 rispettivamente le temperature degli stati finale ed  iniziale del processo. Unendo le formule si ottiene: H2-H1= M C p *(T2-T1).

OSSERVAZIONI:

1.               L’ultimo risultato ,anche se ottenuto per una particolare trasformazione termodinamica,può essere generalizzato.

2.               Dall’ultima formula si vede che l’Entalpia e’ una variabile di stato poiché dipende dalla temperatura iniziale e finale del processo e non dal percorso termodinamico seguito.

3.               Sono rilevanti, in una trasformazione termodinamica,le variazioni dell’Entalpia e dell’Energia interna.Quindi per ottenere valori assoluti di entrambe queste variabili bisogno fissare uno stato di equilibrio arbitrario per il quale i valori di Entalpia e di Energia interna si assumono pari a zero.

 

ENTROPIA

PROCESSI REVERSIBILI

DEFINIZIONE:”Si dice reversibile una trasformazione nella quale si può invertire il verso del processo variando di una quantità infinitesima le condizioni             dell’ambiente circostante”:

 

Si consideri ora una macchina termica ideale che compie trasformazioni reversibili secondo  un ciclo di Carnot :

 

 

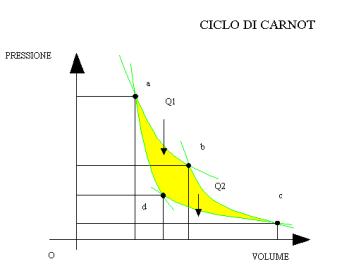
Il teorema di Carnot afferma che:”Il rendimento di una macchina termica che compie un ciclo di Carnot per produrre lavoro ,dipende solo dalla temperatura dei due serbatoi tra i quali opera”.

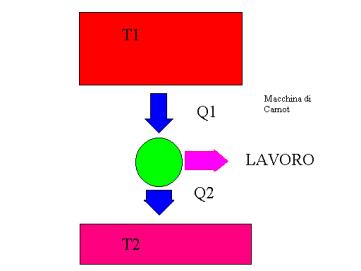
matematicamente il teorema si esprima secondo la formula:

*c      =1-

eguagliando questa espressione con quella generale del rendimento di una macchina termica che opera su un ciclo generico di trasformazioni reversibili:

   *=1 -

si ottiene la formula matematica generale che esprime in maniera più funzionale ai nostri scopi, il teorema di Carnot:

 =

o meglio

+ = 0

si consideri ora una trasformazione ciclica reversibile generica, il ciclo dato può essere approssimato da una serie di cicli di Carnot :

 

 

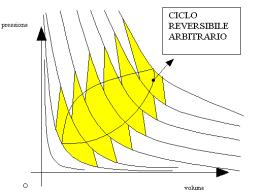
applicando quindi la formula generale del teorema di Carnot suddetta ai diversi cicli considerati in precedenza si ottiene:

= 0

ossia per differenze di temperatura infinitesime tra i cicli della figura precedente:

= 0

definendo quindi la funzione S = dall’ultima formula si ricava che tale funzione e’ una variabile di stato poiché e’ nulla la sua circuitazione su un percorso arbitrario .La funzione S e’ detta ENTROPIA.

OSSERVAZIONI:

1.              dQ non e’ un differenziale esatto poiché il calore scambiato da un sistema dipende dal percorso termico seguito durante una trasformazione.Invece il rapporto  e’ un differenziale esatto come afferma il teorema di Clausius.

2.              L’espressione trovata sopra per l’entropia e’ valida solo nel caso in cui il processo sia reversibile.(vedi dopo il caso del processo irreversibile).

 

PROCESSI IRREVERSIBILI

DEFINIZIONE:”Si definisce processo irreversibile una trasformazione nella quale il passaggio dallo stato iniziale a quello finale non avviene tramite stati di equilibrio intermedi”

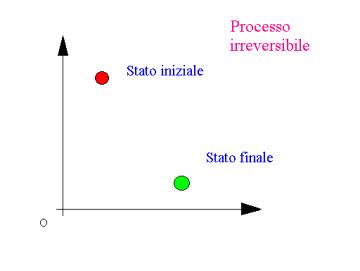
in un processo irreversibile quindi non si può definire l’entropia secondo una formula ben precisa(come nel caso di processi reversibili).Sfruttando però il fatto che l’Entropia e’una variabile di stato (la sua variazione non dipende dal cammino seguito)si può scegliere un percorso termico reversibile che abbia gli stessi stati di equilibrio iniziale e finale di una trasformazione irreversibile e calcolare quindi il “salto” di Entropia su tale cammino .Avremo così la variazione cercata.

 

TEOREMA DI AUMENTO DELL’ENTROPIA:”In una qualsiasi trasformazione termodinamica che evolve tra due stati di equilibrio , la variazione di Entropia del sistema più quella dell’ambiente circostante può restare invariata o aumentare”.

 

OSSERVAZIONI:

1.  L’Entropia rimane costante nei processi reversibili ,cresce in quelli irreversibili.

2.  La variazione entropica di un sistema può diventare negativa purché l’Entropia dell’universo(sistema + ambiente = universo)resti invariata o cresca.

3.  Il Teorema su detto non può essere provato ma si può verificare sempre in tutte le situazioni sperimentali.

 

 

 

ESERCIZI SUL SECONDO PRINCIPIO DELLA TERMODINAMICA

 

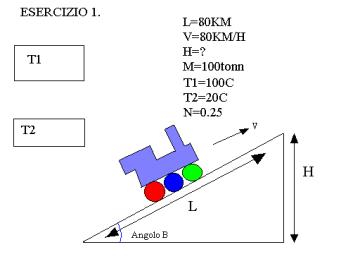
ESERCIZIO N.1:Calcolare l’inclinazione di un piano su cui e’ posto un treno a vapore di 100 tonnellate iniziali che procede alla velocità di 80 km/h sapendo che il piano      lungo 80 km ,il consumo orario di combustibile e’ di una tonnellata all’ora, la caldaia ha una temperatura T1 100°C e l’ambiente una temperatura di 20°C. Sono noti inoltre il rapporto fra il coefficiente economico reale e quello rispettivo di una macchina  di Carnot che opera tra i due serbatoi a temperatura T1 e T2 , pari a = 0.25 e il potere calorifico della macchina pari a 14000 BTU/lb.

RISOLUZIONE:

Ricordiamo  che:

1 lb = 0.4536Kg  1BTU(British Termal Unit) = 1 KJ  quindi il potere calorifico espresso in unità del sistema internazionale e’: 14000  = 30864

la macchina procede ad una velocità di 80 Km/h   quindi  per percorrere 80 Km si spende una  quantità di combustibile pari ad una tonnellata.Ossia un quantità di energia pari a: 30864  1000Kg

di questa energia una parte e’ trasformata in calore , un’ altra in lavoro.Sapendo che,

* =  dove  e’ il coefficiente  economico reale della macchina termica e quello di una macchina termica di Carnot che opera tra i due serbatoi su detti , si può ricavare il coefficiente economico reale della locomotiva a vapore: = 0.054.

          Il lavoro prodotto dalla macchina termica e’ quindi: 0.05430864000 KJ

            Questo lavoro e’ pari all’ energia potenziale acquisita dalla locomotiva per raggiungere l’estremità della salita: M dove M e’ la massa della locomotiva , g la forza di gravità , H l’altezza raggiunta dalla macchina quindi: 1.76 KJ(lavoro della macchina)= 99000 Kg da cui si ricava H=1.812 m.Allora l’inclinazione del piano sarà = arcsinH=1.282°

 

 

            ESERCIZIO N.2:Calcolare il lavoro fatto da una macchina di Carnot che lavora tra due serbatoi :il primo si trova ad una temperatura iniziale di 100°C e il secondo ad una temperatura T costante e pari a 20 °C. La capacità termica dell’acqua a pressione costante e’ pari a 4187.

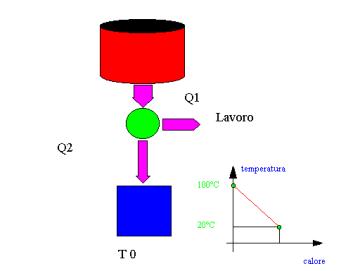
RISOLUZIONE: Il calore Q1 ceduto dal serbatoio e’: Q1 =M

                             Il coefficiente economico della macchina di Carnot e’:

Quindi il lavoro prodotto dalla macchina e’: L = ma il lavoro non e’ costante poiché  la variazione di calore Q1 ceduto dal serbatoio  diminuisce la sua  temperatura in maniera lineare (vedi figura sopra) .Il lavoro infinitesimo prodotto dalla macchina per una variazione infinitesima di temperatura e quindi di calore e’: dL =.

Il lavoro fatto tra il punto 1 e il punto 2 e’: L === M= 1000Kg.