ESERCIZI DI SCAMBIO TERMICO PER IRRAGGIAMENTO

 

 

Nelle lezioni precedenti sono stati individuati tre diversi modi in cui il calore è in grado di propagarsi : per conduzione, per convezione e per irraggiamento.

Questa sezione riguarderà il terzo metodo di scambio termico ed in particolare le sue applicazioni.

Prima di cominciare è però necessario riassumere le principali proprietà di particolari classi di oggetti, per rendere più chiaro lo sviluppo degli esercizi.

 

I corpi grigi

Nel più semplice dei casi ci troviamo a dover risolvere esercizi in cui gli oggetti trattati sono corpi neri.

Sono chiamati così quei corpi che assorbono completamente l’energia raggiante che li colpisce.

Si tratta ovviamente di un caso limite a cui comunque si avvicinano molto il nero fumo ed il nero di platino.

La maggior parte degli oggetti studiati però non sono neri, ma ne esiste una categoria particolare che può essere studiata con relazioni simili a quelle dei corpi neri: i corpi grigi.

Il cofficiente di assorbimento di un copo, indicato con la lettera ‘a’, dipende dalla lunghezza d’onda della radiazione che colpisce l’oggetto, dalla natura della superficie del corpo e dalla sua temperatura.

Questo concetto di dipendenza si esprime tramite formula matematica con:

Nel caso di un corpo nero a =1 per ogni lunghezza d’onda e temperatura.

Sono detti invece corpi grigi, quei corpi per i quali a è costante.

Quindi per un corpo grigio la frazione di energia assorbita è indipendente

dalla composizione spettrale del fascio di radiazioni che colpisce il corpo.

Non bisogna confondere l’aggettivo ‘grigio’, usato in fisica per descrivere il particolare comportamento di un corpo nel fenomeno di scambio del calore, con il colore effettivo di un oggetto, legato invece alla nostra percezione visiva.

Infatti non è detto che un corpo grigio termicamente lo sia anche di colore.

Possiamo considerare approssimativamente come corpi grigi certi oggetti con superficie scabra, diffondenti e non riflettenti, ma che magari percettivamente ci appaiono di un colore diverso dal grigio, a causa della varietà di elementi chimici da cui sono composti .

Ricordiamo anche che le emissioni (poteri emissivi specifici) di un corpo nero e di uno grigio, si indicano rispettivamente con (e 0) e (e ).

 

 

Ora vediamo come sia possibile estendere la legge di Stefan – Boltzmann ad un corpo grigio.

Indichiamo con q0 il potere emissivo integrale del corpo nero.

Quello del corpo grigio diventa:

, (1)

Osserviamo anche che non dipende dalla temperatura: anche se la forma dello spettro varia ad ogni temperatura T, per ogni lunghezza d’onda rimarrà costante il rapporto e /e 0 tra i poteri emissivi specifici .

Utilizzando l’espressione data da Stefan-Boltzmann per il corpo nero e sostituendola nella (1) a q0 si ottiene:

(2)

La formula (2) risulta differire da quella per un corpo nero solo per il coefficiente a, che questa volta non è più uguale ad 1.

Ora stiamo trattando un coefficiente a <1, perciò una parte della radiazione ricevuta verrà riflessa.

Consideriamo una radiazione qinc incidente un corpo grigio.

Conformemente a quanto visto, vi sarà una parte di energia riflessa pari ad

(1-a) qinc mentre solo una quantità aqinc verrà assorbita (Fig.1).

Fig.1 – Esempio di scambio termico di un corpo grigio

 

Quando in un esercizio ci troveremo di fronte ad un corpo grigio si dovrà tenere conto della frazione di energia riflessa; il fatto che a sia costante su tutto lo spettro e indipendente dalla temperatura,sarà il dato che semplificherà i nostri calcoli .

Anche la legge di Lambert per il corpo nero ( Indicando con in l’intensità d’irradiazione nella direzione normale alla superficie e con ia l’intensità dell’irradiazione in una direzione che forma l’angolo alfa con la normale) è rispettata nel caso di un corpo grigio.

Ormai risulta chiaro che un corpo grigio rispetta tutte le leggi del corpo nero, con uno scostamento (comunque misurabile) di un unico numero che è il coefficiente a costante per tutte le frequenze e le direzioni dello spazio.

Le seguenti considerazioni riguardano la riflettenza dei corpi.

Data una superficie con un definito grado di specularità e un raggio incidente, dopo l’impatto si ha un’emissione diffusa (riflessione diffusa) secondo un certo schema geometrico che viene detto solido fotometrico, ma si ha anche una parte di emissione discreta (riflessione speculare) con una direzione ben precisa.

Nel caso della riflessione speculare l’angolo di incidenza J i della radiazione è uguale all’angolo di riflessione J r (fig.2)

Se poi il corpo è semitrasparente , si ha anche il fenomeno della rifrazione.

 

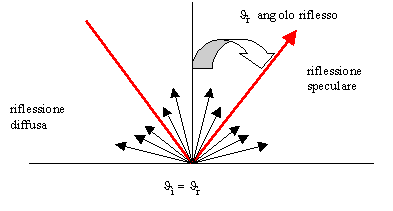
Fig.2 – I due diversi tipi di riflessione.

E’ importante sapere che non esistono corpi che presentano solo riflessione speculare, viceversa ne esistono altri che hanno solo la componente diffusa.

Nel campo dell’irraggiamento termico, se dovessimo considerare ed analizzare la riflessione speculare avremmo calcoli complicati, per questo si cerca sempre (quando possibile) di trascurarla.

Nei modelli si considerano perciò solamente corpi grigi (che hanno solo la componente di riflessione diffusa), ricordando però che la maggior parte dei corpi reali non sono grigi e hanno una quota di riflessione non diffusa che spesso non è trascurabile.

Si deve perciò prevedere e accettare che i risultati teorici e quelli reali sperimentali divergano notevolmente tra loro.

A questo punto possiamo iniziare a vedere lo svolgimento di alcuni esercizi fondamentali nella trattazione dell’argomento di scambio termico per irraggiamento.

 

ESERCIZIO 1

Analisi dello scambio termico tra due superfici piane completamente affacciate:

Consideriamo due superfici grigie, diffondenti, infinite, in modo da poter trascurare gli effetti di bordo, che siano completamente affacciate.

Supponiamole a temperature diverse T1 e T2 con coefficienti di assorbimento a1 e a2 (Fig.3).

Consideriamo per primo il caso più semplice di due superfici completamente nere, separate dal vuoto (quindi non vi saranno fenomeni di convezione).

a) I coefficienti di assorbimento a1 ed a2 delle due superfici risultano in questo caso uguali e di valore pari ad 1 (proprietà dei corpi neri vista in precedenza, dovuta al fatto che tutta l’energia ricevuta dal corpo viene assorbita)

Fig.3 – Modello di scambio termico fra corpi assolutamente neri

Abbiamo indicato con q1 la quantità di calore irraggiata dal corpo 1

e con q2 la quantità uscente dal corpo 2.

Esse sono diverse per ipotesi, in quanto stabilito che i due corpi si trovassero a temperature differenti.

Ricordiamo che stiamo lavorando con dei corpi neri, quindi, ogni radiazione emessa da un corpo verrà interamente assorbita dall’altro (per ora non vi sono fenomeni di riflessione).

Dalla legge di Stefan – Boltzmann abbiamo che:

(3)

. (4)

Le due equazioni sovrascritte sono collegate da una relazione che potrebbe tornarci molto utile:

(5)

Indicando con qs1 la potenza scambiata per irraggiamento dal corpo 1, questa relazione è data dalla legge di Prèvost (detta anche degli scambi) secondo la quale la potenza (energia per unità di tempo) scambiata termicamente dal corpo 1 è uguale alla potenza irradiata dallo stesso, a cui va sottratta la quantità da esso assorbita, che in questo caso è tutta quella emessa dal corpo 2.

Analogamente posso ricavare la potenza scambiata dal corpo 2.

Quindi, combinando le equazioni (3), (4), (5), arrivo a scrivere che:

 

(6)

b) Adesso passiamo al caso un po’ più laborioso di un corpo nero in relazione di scambio termico con uno grigio.

Ci aspettiamo già che quest’ultimo rimandi ‘al mittente’una parte di energia ricevuta.

Ricordiamo inoltre che a1 (coefficiente di assorbimento del corpo nero) rimarrà uguale ad , mentre a2 <1.

Osservazione: Nel caso dell’irradiamento termico è possibile mantenere invariato col tempo lo stato fisico dei corpi che scambiano energia se si compensano le quantità di energia scambiate per irradiamento con quantità di calore, cioè se si fa in modo che risulti uguale a zero la somma algebrica delle quantità di energia scambiate per irradiamento e per trasmissione di calore in un intervallo di tempo qualunque.

Per questo motivo gli scambi di energia per irradiamento termico possono essere considerati come equivalenti a scambi di calore.

 

 

 

 

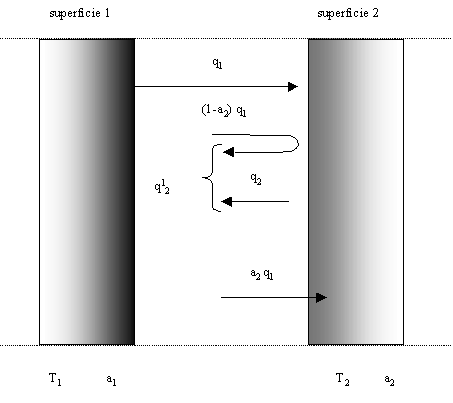
Fig.4 – Modello di scambio termico tra un corpo nero ed uno grigio

 

Il corpo grigio 2, assorbe solamente la frazione di calore a2 q 1 su un totale di q 1 emessa dal corpo nero (corpo 1) e ne riflette una quota pari ad , che torna sul corpo 1 assieme alla quantità q2 emessa da 2 (come possiamo osservare in (Fig.4).

Quindi sul corpo 2 arriva complessivamente una quantità:

(7)

e siccome il coefficiente di riflessione di un corpo è pari ad (1- coefficiente di assorbimento), possiamo riscrivere la (7) anche come:

(8)

Analogamente al punto a) possiamo applicare la relazione di Prevost sul corpo nero 1 (la applichiamo al corpo nero per comodità) ed esprimere tutto in funzione di s 0 e delle temperature T utilizzando la legge di Stefan-Boltzmann:

(9)

perciò:

(10)

Ora non ci resta che analizzare il caso di scambio termico tra due corpi grigi.

c) Ovviamente in questo caso i fenomeni di riflessione saranno notevoli, i due corpi infatti si comporteranno come due specchi (il paragone non è molto corretto ma rende bene l’idea) a confronto, rimandandosi infinite volte frazioni sempre più ridotte di energia (infatti solo parte della radiazione ricevuta da un corpo grigio viene riflessa).

Siamo nel caso in cui sia a1 che a2 sono <1, e diversi tra loro.

Fig.5 – Modello di scambio di calore tra corpi grigi

 

In figura 5 non sono stati riportati, per mancanza di spazio, tutti i passaggi che il calore compie.

E’ ormai chiaro però che la radiazione ‘rimbalzi’ più volte tra i due corpi frazionandosi ogni volta (infatti ogni volta la radiazione incidente ritorna moltiplicata per un fattore <1) fino a divenire pressoché trascurabile.

NB: in realtà ,come avviene per lo studio dell' acustica , bisognerebbe considerare questo caso come un transitorio cioè studiare tutti i possibili rimbalzi energetici passo dopo passo.

Però negli studi di scambio del calore tali fenomeni avvengono talmente rapidamente che fare un bilancio finale non comporta l' insorgere di un errore rilevante.

Questa volta per entrambe le pareti in figura 5 dobbiamo impostare un’equazione che riassuma, come somma algebrica, la quantità di energia scambiata dai due corpi Possiamo dunque scrivere:

. (11)

E’ un sistema di due equazioni in due incognite; il metodo più immediato per risolverlo è per sostituzione e così facendo si ottiene:

. (12)

Scrivendo la relazione di Prevost per la superficie 1, sostituendovi la (12) e semplificando otteniamo:

, (13)

riscrivendola poi in funzione di s 0 e delle temperature, diventa:

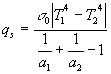. (14)

Siamo giunti al risultato voluto!

Infatti la (14) è la relazione che determina lo scambio termico tra due lastre piane parallele grigie.

Ai fini della soluzione del nostro esercizio non è importante la distanza alla quale si trovano le due lastre purchè esse non siano a contatto, poiché in tal caso si avrebbe scambio di calore anche tramite conduzione.

 

 

ESEMPIO NUMERICO :

 

In questo esempio diamo dei dati numerici per renderci conto di cosa succede dimensionalmente

T1=400K a1=0.8

T2=300K a2=0.6

Sostituiamo cioè nell' equazione trovata precedentemente valori che potremmo trovare in un problema reale otteniamo :

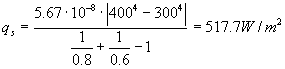(15.a)

Se consideriamo anche i movimenti convezionali:

Nu = C Cpa Prb (15.b)

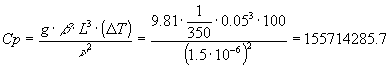
dove è la temperatura media e la viscosità dell’aria.

Sostituendo il risultato ottenuto nella (15.b) otteniamo:

(15.c)

(16)

Se aumento T1 e T2 in modo tale da mantenere costante la loro differenza, la quantità qs si innalza superando quella data da qc.

Ad alte temperature, come ad esempio nella camera di combustione di una caldaia, dove la fiamma ha una temperatura di 1800 0 C, lo scambio di calore per convezione costituisce una bassissima percentuale.

Osservazione: se nello spazio tra i due corpi non ci fosse il vuoto ma fosse presente un fluido, il calore si scambierebbe sia per irraggiamento che per convezione.

In tal caso dovremmo supporre l’esistenza di due resistenze termiche:

una di convezione, lineare con la temperatura, ed una di tipo radiante che non è lineare.

Finora abbiamo supposto il caso di superfici completamente affacciate, del resto il requisito fondamentale perché due corpi scambino calore per irraggiamento è che essi ‘si vedano’.

Però può essere che due corpi non siano completamente affacciati, ma che lo siano solo parzialmente.

E’ questo il caso che andiamo ad analizzare.

 

Irraggiamento tra superfici parzialmente affacciate

Consideriamo il caso di una cavità, che potrebbe rappresentare una stanza oppure la camera di combustione di un forno, e che contiene un corpo (Fig.6).

Sia la cavità che il corpo al suo interno sono grigi per ipotesi.

Per semplificare i calcoli facciamo l’ulteriore ipotesi che il corpo sia convesso, in modo tale che non possa scambiare calore per irraggiamento con se stesso, e che la cavità sia concava.

 

Fattore di vista o di forma

Definiamo subito il fattore di vista come

, (17)

un numero puro che esprime il rapporto fra la potenza che partendo dalla superficie del corpo 1 va a colpire 2 e la potenza totale emessa da 1.

La somma di tutti i fattori di vista tra superfici deve dare 1 in accordo con il principio di conservazione dell’energia, quindi, dato un fattore di vista, esiste sempre il suo complementare.

Questa frazione è quindi basata sull' ipotesi che la radiazione recepita da una superficie è proporzionale all' angolo solido sotto cui viene vista essa stessa dalla sorgente.

Esiste anche un fattore di forma particolare F11 che è definito come frazione della radiazione della superficie 1 che colpisce la superficie stessa ; per i corpi convessi più comuni questo varrà ovviamente zero.

Il fattore di vista , nella sua forma più generale, sarà sempre minore uguale ad 1.

Osservazione: Il caso visto in precedenza delle due superfici piane parallele evidentemente implicava un fattore di forma uguale ad uno.

Questo nuovo parametro ci permetterà di studiare lo scambio termico per irraggiamento fra due e più corpi tenendo in considerazione proprietà ,come l' orientazione relativa tra superfici ,che altrimenti rappresenterebbero un problema assai complesso.

Ad esempio :

se ho un corpo 1 ed un corpo 2, sferici, che si scambiano calore accade che parte della potenza emessa dal corpo 1 viene recepita dal corpo 2 mentre un' altra parte si perde; questo è dovuto al fatto che la trasmissione del calore per irraggiamento tra due superfici ha una sua orientazione.

Basti notare come cambia la nostra percezione del calore a seconda di come ci si pone (di fronte o lateralmente) nei confronti di una sorgente (come ad esempio l’apertura di un caminetto).

 

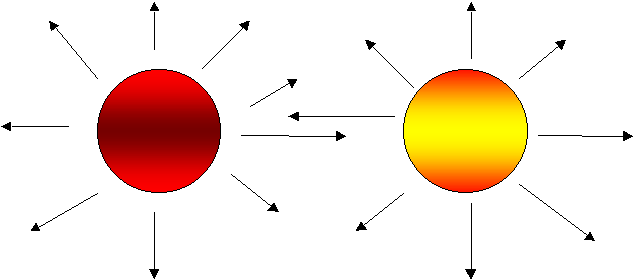
Fig.6 – Orientazione dell’irraggiamento

A questo punto è utile trattare alcuni casi particolari:

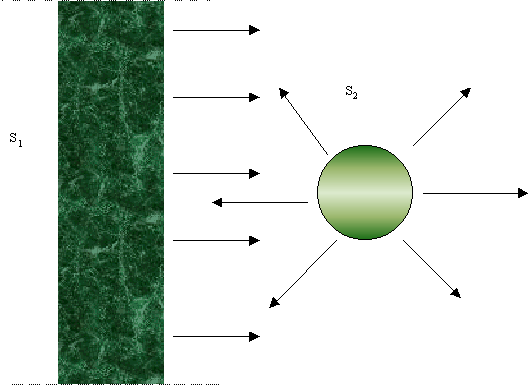
  1. Superficie piana infinita, di superficie S1 in scambio termico con una sfera di superficie S2 , di dimensioni molto inferiori (Fig.7).

    2.  

    Fig.7 -Scambio termico tra due corpi di dimensioni molto differenti

    (18)

    Invece F21 vale 0,5 poiché metà della potenza dalla sfera quella emessa dall' emisfero che non si affaccia su S1 si disperde.

  2. Superficie chiusa costituita da più parti indipendenti tra loro (Fig.8)

    3. ogni elemento agisce come se fosse indipendente, pur facendo parte dello stesso corpo concavo.

    Così ogni parte interagisce con le altre scambiandosi calore per irraggiamento.

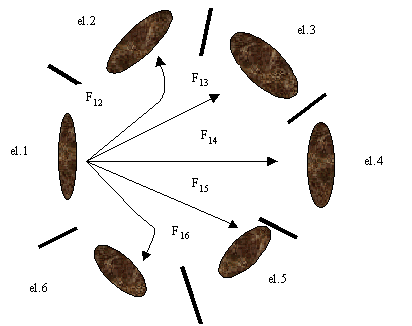
    Fig.8 – Corpo concavo ad elementi indipendenti interagenti tra loro.

     

    Come si può facilmente vedere in figura 8, ogni parte cede energia alle altre, tant' è che svolgendo un semplice bilancio si ottiene che :

    (19)

    Osservazione: una o più parti di un corpo concavo potrebbero essere esse stesse concave, in tal caso basterà aggiungere nella sommatoria il fattore di vista dell’elemento in questione con se stesso

    Dividendo ambo i membri della (19) per Q1 si ottiene

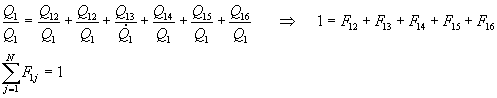    (20)

    Dalla sommatoria deduciamo che la potenza è equilibrata.

    Tale relazione vale qualsiasi sia il numero di superfici interagenti, possiamo quindi riassumere quanto detto enunciando la regola della somma:

    la somma dei fattori di vista della superficie i di una cavità verso tutte le superfici della cavità ,essa stessa inclusa, è uguale ad uno.

  3. Consideriamo ora il caso di una cavità, che potrebbe essere una qualunque

stanza o la camera di combustione di un forno, che contiene un corpo.

Sia il corpo esterno che quello interno sono corpi grigi.

Per semplificare facciamo l’ipotesi che il corpo sia convesso (non può irraggiare su se stesso) e la cavità sia concava.

 

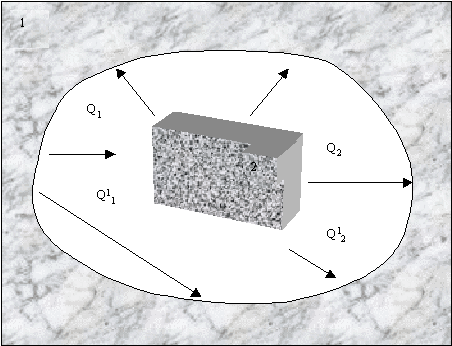
Fig.9 – Scambio termico tra oggetto grigio convesso contenuto in corpo concavo

 

 

F21 vale ovviamente 1 poiché tutte le radiazioni emesse da 2 cadono sul corpo 1, mentre F12 non è pari ad 1 perché una frazione dell' energia emessa da 1 ricade su di esso, essendo S2 (superficie del corpo 2) piuttosto ridotta, quindi F12<<1

Studiamo meglio questa situazione:

chiamiamo Q1 e Q2 le potenze emesse da ciascuna superficie, mentre Q11 e Q12 le quantità complessive di energia che vanno a colpire i due corpi.

A questo punto possiamo imporre il sistema:

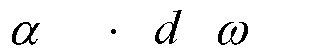(21)

ancora una volta il metodo più indicato per la risoluzione di questo sistema di due equazioni in due incognite è per sostituzione, otteniamo:

; (22)

ricordando che è F21=1 e F11=1-F12 e utilizzando la relazione di Prevost per ricavare la potenza scambiata complessiva, si ha:

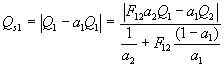. (23)

Possiamo fare un’ulteriore sostituzione:

, , (24)

quindi la (23) equivale alla relazione:

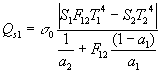, (25.a)

che nel caso di superfici completamente affacciate (F12=1 e S1= S2), considerando qs anziché mi permette di ottenere

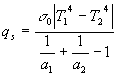(25.b)

che, come possiamo notare, è lo stesso risultato del primo esercizio.

La relazione (25) consente di determinare rapidamente il valore di F12; infatti se T1=T2, deve essere anche Qs= 0, per cui si annulla il numeratore della (25) e deve essere:

. (26)

E’ una relazione che vale solo se il corpo 2 è convesso (altrimenti parte delle radiazioni ricadrebbero su di se e i nostri calcoli precedenti non sarebbero più validi) e se entrambe le superfici si trovano alla stessa temperatura (isoterme).

Consideriamo il caso particolare di S1/S2 molto grande, cioè F12<<1.

Nella (25) posso trascurare il secondo termine al denominatore; andando ora a sostituire questa relazione: S2=F12S1 si ottiene:

. (27)

Osserviamo quindi che per un corpo dentro un ambiente grande, dove sia il corpo che l’ambiente sono grigi, si ottiene una relazione come se esso fosse contenuto in un corpo nero.

Questo risultato è molto importante in quanto spesso ci capita di avere a che fare con ambienti grandi come ad esempio può essere la camera di combustione di una caldaia oppure un forno.

Prima di procedere è opportuno precisare che in un caso più complesso dovrò fare degli integrali di superficie.

La parte della potenza emessa da un elemento di superficie dS (per la quale valga la legge di Lambert) che investe un generico elemento di superficie dSè espressa da cos indicando concon in l’intensità di emissione in direzione normale, con l’angolo che la congiungente gli elementi dSi e dS1 fa con la normale a dSi e con d,l’angolo solido sotto cui è visto dS1 da dSi.

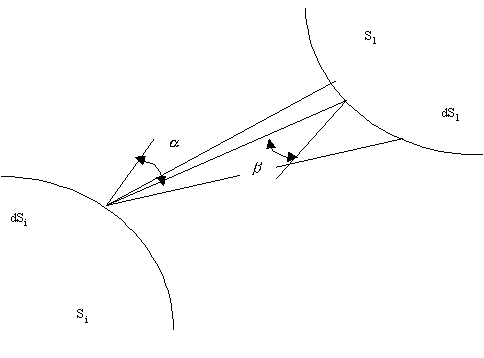
Fig.10 – Scambio di radiazione tra elementi infinitesimi di superficie.

 

Ovviamente si ha , dove r è la distanza tra i due elementi di superficie e l’angolo fatto dalla congiungente i due elementi con la normale a dS1.

 

 

 

 

Esercizio 2

Consideriamo un forno rotante per la cottura del cemento: si tratta, schematicamente di un cilindro rotante attorno al suo asse.

Lo scambio termico sulle facce è trascurabile poiché la dispersione del calore avviene solo lateralmente.

Determinare la potenza dispersa dal forno.

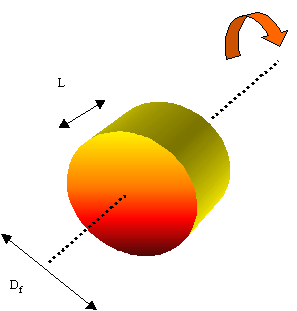
Fig.11 – Forno rotante per la cottura del cemento

Dati del problema :

Df=1.5m

L=5m

Tp=523K

Tinfinito=300K (temperatura dell’ambiente all’infinito)

a=0.8

In questo caso la soluzione è immediata, infatti:

= (28)

con S=DfL

Questa potenza dissipata risulta essere eccessiva; per ridurla si installa un secondo tubo formato da un foglio di lamiera zincata (non rotante) il cui diametro Ds è 2.25m e il cui coefficiente di assorbimento as è 0.4

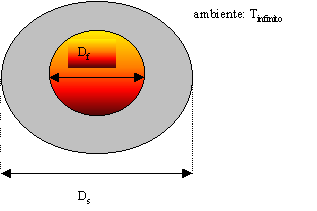
Fig.12 – Sezione del forno schermato

 

 

Ora però avrò un passaggio intermedio, quello tra forno ed involucro.

 

 

 

 

La prima resistenza rappresenta lo scambio di calore tra forno e schermatura, la seconda quello tra schermo ed ambiente.

Chiamando le superfici del forno e della lamiera rispettivamente Sf e Ss possiamo risolvere rapidamente il problema, dove la nostra nuova incognita sarà la potenza Q2.

Lo schermo stesso ha una resistenza termica conduttiva (infatti lo schermo ed il forno sono a contatto) che però è trascurabile in questo caso.

La potenza scambiata sarà

(29)

Dobbiamo utilizzare l’equazione trovata in precedenza, nel caso di due superfici confrontabili tra loro.

Uguagliando quest' espressione con la (29), si ottiene un’ equazione che ha come unica incognita TS

 

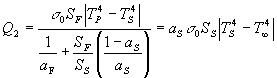(30)

 

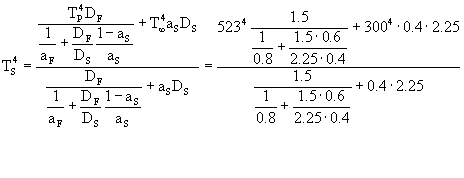(31)

Adesso sappiamo che Ts = 437K, e questo dato ci permette di trovare con una delle due equazioni trovate ,in questo caso la (30),

(32)

Si è quindi ridotta di più di un terzo la potenza scambiata senza introdurre alcun isolante.

Questa riduzione non è dovuta tanto alla resistenza termica della lamina, ma allo step intermedio che il calore deve compiere.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Esercizio 3

 

 

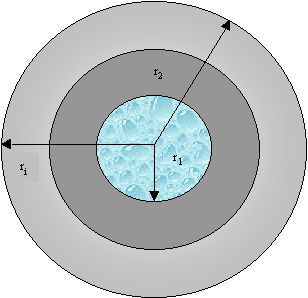
Fig.13 – sezione del tubo

 

Dati:

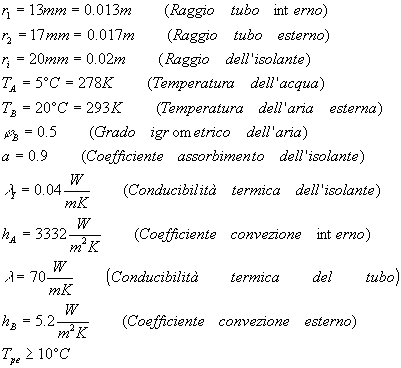
(Temperatura di parete esterna)

 

 

 

 

 

 

 

 

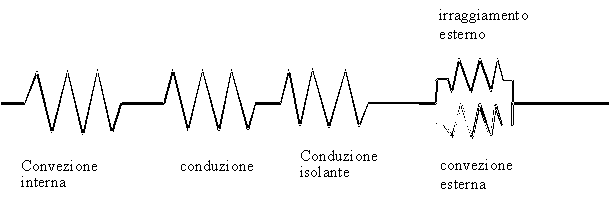
Questo è lo schema di un circuito elettrico equivalente al caso del nostro esercizio.

Andiamo a stimare le resistenze che entrano in gioco:

(33)

 

(34)

 

(35)

 

dove Pr è il valore di Prandtl quando l’acqua si trova a 50C.

Trovimo il coefficiente di convezione interna:

(36)

la resistenza di convezione interna, quindi, avrà un valore molto basso:

(37)

ora calcoliamo la resistenza della prima conduzione presente nel sistema, ovvero quella tra liquido e tubo:

(38)

 

le due resistenze sono dello stesso ordine di grandezza e, come vedremo, saranno trascurabili rispetto alle successive.

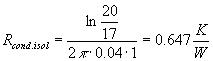(39)

 

Ora calcoliamo il coefficiente di convezione esterna che andremo poi a sommare a quello di irraggiamento per ottenere l’induttanza totale equivalente esterna.

Calcoliamoci il numero di Grashof:

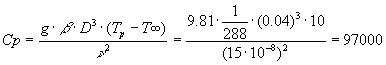(40)

calcoliamo poi il numero di Nusselt ricordando la (15.b):

(41)

adesso siamo in grado di calcolare il coefficiente di convezione esterna:

(42)

ora devo calcolare quello di irraggiamento.

Usando la formula semplificata per l’irraggiamento (non lineare):

(43)

Dalla definizione di coefficiente di irraggiamento so che :

(44)

quindi sostituendo numericamente si ha:

(45)

A questo punto posso sommare i due coefficienti:

htot = he + hr = 12.04 W/ m2K (46)

se volessi calcolare la resistenza totale esterna :

(47)

Nella nuova rete elettrica equivalente, il fatto di avere introdotto una resistenza in parallelo rispetto a quella convettiva, non comporta nessun cambiamento nella risoluzione del problema, se non dal punto di vista numerico.

Se ci fosse solo quella convettiva infatti avrei:

Rtot = 0.647+0.7879 = 1.434 K/W (48)

con l’aggiunta della resistenza dovuta all’irraggiamento invece risulta:

Rtot = 0.647+0.29 = 0.937 K/W. (49)