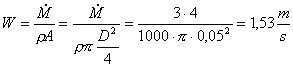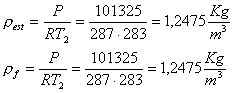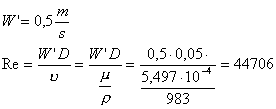Esercizi di fluidodinamica

 

Indice

 

Esercizio 1) autoclave                                                                    pag.        -1-

Esercizio 2) caminetto                                                                    pag.        -4-

Esercizio 3) impianto di aerazione                                       pag.        -8-

Esercizio 4) impianto a circolazione naturale                                   pag.      -11-

 

Esercizio 1

 

Si consideri un sistema costituito da :

·        n° 1 serbatoio aperto;

·        n° 1 serbatoio chiuso (autoclave);

·        n° 1 pompa.

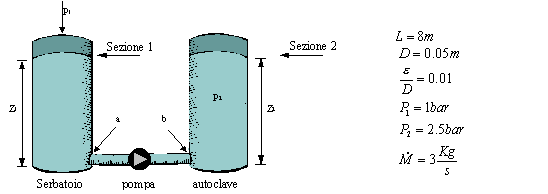
Tramite una pompa si carica l’autoclave prelevando l’acqua dal serbatoio aperto; l’autoclave viene mantenuta alla pressione P2. Il condotto che collega i serbatoi ha una sezione circolare, una lunghezza L, un diametro D e una scabrezza relativa e/D. Si chiede di calcolare la prevalenza DP e la potenza P della pompa conoscendo la sua portata in massa M.

 

L'esercizio si risolve impostando l'equazione del bilancio dell’ energia dei sistemi aperti:

 

                                                       (1)

dove:

           è l’accelerazione gravitazionale

     è la densità del fluido contenuto nel serbatoio, cioè acqua

W1 e W2                sono le velocità dei peli liberi rispettivamente del serbatoio e dell’autoclave.

Come tutti i problemi basati sull’equazione del bilancio dell’energia dei sistemi aperti una scelta opportuna delle sezioni semplifica lo svolgimento del problema infatti, scegliendo come sezioni i peli liberi del serbatoio e dell’autoclave , possiamo trascurare il salto di quota H e la differenza di velocità tra W2 e W1:

 



e la 1) diventa:

 

                                                                                                (2)

in questa equazione l’unica incognita che ci separa dal conoscere la prevalenza è R vale a dire le perdite del sistema. Utilizzando il concetto di lunghezza equivalente, le perdite sono date da:

 

                                                                                               (3)

dove:

 

x              è il fattore di attrito (da determinare)

Leq            lunghezza equivalente dell’imbocco a) e dello sbocco b) (da determinare)

W             è la velocità del fluido (da determinare)

 

Per determinare la velocità W si utilizza la definizione di portata in massa da cui deriva:

 

                                                    (4)

utilizzando W, si calcola il coefficiente di Reynolds:

 

                                                                       (5)

infine, avendo a disposizione la scabrezza relativa e il numero di Reynolds, si ricava il fattore di attrito dal diagramma di Moody:

 

                                                                                                          (6)

Per risolvere la 3) si deve calcolare Leq che è costituita da due contributi:

·        Leq1 dovuto allo sbocco a) (vedi schema)

·        Leq2 dovuto allo sbocco b) (vedi schema)

 

Dalle tabelle risulta:

 

                                                                                                      (7)

per cui la lunghezza equivalente totale sarà:

 

                                                                                    (8)

 

Si hanno a disposizione tutti i dati necessari per il calcolo delle perdite dunque, utilizzando la 3) si ottiene:

 

                             (9)

unendo la 2) e la 9) si può calcolare la prevalenza della pompa:

 

       (10)

 

La potenza teorica della pompa è:

 



dove:

 

                è la portata in volume della pompa

 

Assumendo un rendimento della pompa pari a  la potenza effettiva della pompa risulta essere:

 

 

Esercizio 2

 

Si consideri un impianto di riscaldamento a camino caratterizzato dai seguenti dati:

 

 


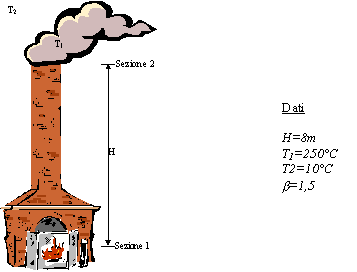
dove:

H              è la differenza di quota tra il centro della bocca del camino e lo sbocco della canna fumaria

T1             è la temperatura del fumo prodotto dalla combustione della legna

T2             è la temperatura esterna

b              è il coefficiente di perdite concentrate dell’intero sistema

 

Nel camino entra aria che viene riscaldata fino ad una temperatura di 250°C; l’aria calda,essendo più leggera del fluido circostante, sale lungo la canna fumaria. Si determini la velocità W dei fumi.

 

Soluzione

 

Ipotesi:

·           La canna fumaria è sufficientemente isolata tanto da mantenere costante la temperatura del fumo lungo il tragitto

·           Nel camino entra 4¸5 volte la quantità stechiometrica di aria che serve alla combustione dunque, ciò che verrà chamato fumo è in realtà un fluido che ha le stesse proprietà termodinamiche dell’aria.

·           Si scelgono le sezioni,come in figura, in base alle quali si scriverà l’equazione del bilancio dell’energia.

·           La canna fumaria solitamente non è rigorosamente verticale ma è costituita da raccordi e tratti inclinati dunque si assume una lunghezza

 

Osservazione

Solitamente si trascura il salto di pressione relativo a una differenza di quota così effimera però, in questo caso, facendo questa semplificazione si arriverebbe all’assurdo di una velocità dei fumi pari a zero. Infatti la piccola differenza di pressione, dettata anche dal fatto che l’aria più calda del camino ha densità minore, funge da motore dell’impianto.

 

All’esterno del camino valgono le leggi della fluidostatica, dunque:

 

                                                                                                 (1)

 

dove:

P1             è la pressione nella bocca del camino

P2             è la pressione esterna

rest            e la densità dell’aria esterna

g               è l’accelerazione gravitazionale

 

Calcolo della densità dell’aria alle due temperature utilizzando l’equazione dei gas:

 

                                                                   (2)

 

dove:

 

rf              è la densità dei fumi

R               è la costante universale dei gas

 

Dunque, valutata da fuori ho una differenza di pressione

 

                                                      (3)


è come avere una pompa con questa prevalenza.

Considerando che non esiste una pompa fisica che produce lavoro, si conoscono tutti i termini per poter scrivere l’equazione del bilancio energetico:

 

                                                                       (4)

si può operare una semplificazione dovuta alla scelta delle sezioni infatti, la bocca del camino ha una sezione molto più grande della sezione di sbocco della canna fumaria e quindi la velocità del fumo W1 è trascurabile rispetto a W2. Sostituendo la 3) nella 4) e sapendo che le perdite di carico sono espresse da

 

 

                                                                                              (5)

 

 

otteniamo

 

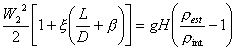                                                                  (6)

 

Dalla 6) si può ricavare la velocità dei fumi conoscendo il valore del fattore d’attrito di seguito calcolato.

Il secondo membro dell’equazione 6) costituisce il motore del sistema mentre, il primo membro è la resistenza da vincere; il camino avrà un buon tiraggio se il motore riesce a prevalere sulla resistenza.

La 6) è un’equazione con 2 variabili,dunque per risolverla si dovrà intraprendere una soluzione ricorsiva. Inizialmente si fissa una portata e a una velocità del fumo minima, per verificare che il motore sia sufficiente a realizzarla, successivamente si giunge al valore reale della velocità con metodo ricorsivo.

Supponendo che in 1 ora vengano bruciati 10Kg di legna e sapendo che la quantità stechiometrica di aria necessaria a bruciare 1Kg di legna è 14Kg, si può ricavare la portata in massa minima che il sistema deve avere:

 

                                                                 (7)

 

Dalla definizione di portata in massa e dalla 7) si ricava la velocità Wmin dei fumi relativa alla portata minima:

 

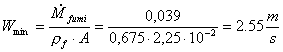                                                      (8)

 

dove

 

     è l’area della sezione di passaggio della canna fumaria

 

Per giungere al valore della resistenza minima del sistema si deve calcolare il fattore d’attrito e per questo serve il numero di Reynolds:

 

                                                                              (9)

 

dove

 

n              è la viscosità dell’aria a 250°C (coincide con quella del fumo)

 

Considerando la 9) e la scabrezza relativa della canna fumaria pari a  si ricava il fattore di attrito sul diagramma di Moody:

 

                                                                                                                      (10)

 

Dunque la resistenza minima da vincere, che è il primo termine dell’equazione 6), è:

 

                         (11)

 

 

Il motore a disposizione, che è il secondo termine dell’equazione 6), è

 

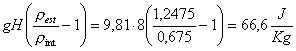                                                 (12)

 

Si vede che il motore è sovrabbondante di un fattore @4 rispetto alla resistenza e ciò indica che la portata è maggiore di quella minima prevista.

Ne deriva che la velocità con cui esce il fumo dalla canna fumaria è maggiore di quella ipotizzata. Per calcolare la velocità reale bisogna eseguire ricorsivamente i seguenti passi:

 

1.      calcolo del numero di Reynolds (utilizzando l’ultima velocità trovata)

2.      calcolo del fattore di attrito (utilizzando il punto 1 e )

3.      calcolo della nuova velocità W2’

4.      ritornare al punto 1.

 

I risultati di qualche iterazione sono riportati nella tabella seguente.

 

W2

Re

x

W2’

2,55

9064

0,047

5,08

5,08

18056

0,044

5,16

5,16

18358

0,043

5,19

5,19

18463

0,043

5,19

 

Si nota che dopo pochi cicli la velocità si stabilisce intorno ad un valore che è quello reale, naturalmente bisogna considerare un margine di errore su questo risultato in quanto, l’ausilio del diagramma di Moody, non porta a valori esatti ma stimati da chi lo interpreta.

La velocità del fumo è circa doppia di quella minima necessaria cioè, nel camino entra più aria di quella che serve; bisogna notare che l’aria che fluisce dal camino è aria calda presente nell’ambiente dove il camino è installato e che una uguale quantità di aria fredda entra dall’esterno per compensare quella uscita. Concludendo non bisogna far aspirare dal camino più aria di quella che serve poiché l’aria fredda che entra raffredda l’ambiente. Dunque, bisogna intervenire sulla quantità di fumi uscenti utilizzando saracinesche nella canna fumaria o agendo sulle griglie di regolazione delle prese d’aria.

 

Esercizio 3

 

Si consideri un impianto di aerazione che preleva l’aria da un locale e la convoglia in un altro con l’ausilio di un ventilatore. Dimensionare la macchina cioè indicarne prevalenza e potenza.

 

 

 

 

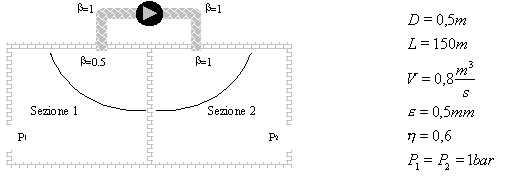
dove:

 

·          D                        è il diametro del condotto

·          L                         è la lunghezza del condotto

·                                 è la portata in volume del ventilatore

·          e                         è la scabrezza del condotto

·          h                                    è il rendimento del ventilatore

·          P1, P2                sono le pressioni dei due locali

·          b                                    è il coefficiente di perdite concentrate

 

Il problema si risolve utilizzando l’equazione del bilancio dell’energia, quindi si utilizza una scelta delle sezioni come in figura per semplificare l’equazione.

 

                                                       (1)

dove:

           è l’accelerazione gravitazionale

W1 e W2                sono le velocità dell’aria nelle sezioni utilizzate.


Osservazione:

la densità dell’aria andrebbe calcolata con l’equazione dei gas perfetti ma, viene assunta per semplicità come:

 

Questa scelta di sezioni porta a trascurare i primi due termini della 1); il terzo termine diviene nullo in quanto i due locali sono aperti e quindi alla stessa pressione, dunque:

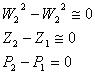                                                                                                     (2)

 

e la 1) diventa

 

                                                                                                               (3)

 

dove

 

·          DP                      è la prevalenza cercata

·          R                        rappresenta le perdite di carico

 

Le perdite di carico sono

 

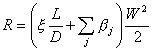                                                                                       (4)

 

dove

·          W                       è la velocità dell’aria (assegnata perché è nota )

·          x                        è il fattore di attrito (da determinare)

 

Calcolo della velocità dalla definizione di portata in volume

 

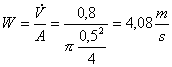                                                                                  (5)

 

dove

 

·          A                        è l’area della sezione del condotto dell’aria

 

È doveroso notare che, senza i dovuti accorgimenti acustici, con una velocità così elevata l’impianto potrebbe essere rumoroso.

Si procede calcolando il numero di Reynolds (Re) e la scabrezza relativa (e/D) per determinare il fattore di attrito:

 

                                                                        (6)

                                                                                               (7)

 

Con l’ausilio del diagramma di Moody si determina il fattore di attrito:

 

                                                                                                                        (8)

 

Sono presenti tutti i termini per calcolare le perdite di carico:

 

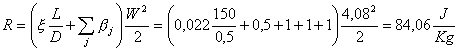          (9)

 

Dalla 3) si ricava la prevalenza del ventilatore:

 

                                                                        (10)

 

La potenza teorica è:

 

                                                                          (11)

 

Infine, la potenza reale è:

 

                                                                                   (12)

 

Esercizio 4

 

Si consideri un impianto di riscaldamento a circolazione naturale costituito da una caldaia e un corpo scaldante (termosifone). Si determini qual è la potenza termica (Q) che la caldaia da all’ambiente per mezzo del corpo scaldante.

 

 

 

 

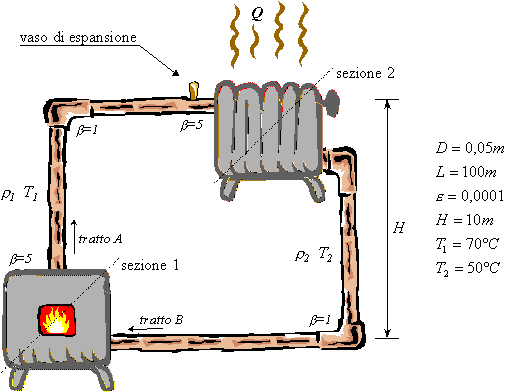
Il condotto del sistema è un tubo in ghisa molto grosso, rispetto ai tubi utilizzati nei normali impianti domestici, infatti, l’impianto a circolazione naturale non necessita dell’utilizzo di una pompa per far circolare l’acqua; il motore del sistema è la differenza di temperatura (DT) tra la temperatura dell’acqua che esce dalla caldaia (T1) e la temperatura dell’acqua che esce dal corpo scaldante (T2).

Si ipotizza che non ci siano dispersioni di calore dai tubi cosicché, la quantità di calore ceduta è solo quella dovuta al termosifone. Dunque, la differenza di temperatura tra l’acqua che entra e quella che esce dal termosifone è:

 

 

La potenza termica che la caldaia da all’ambiente per mezzo del corpo scaldante è:

 

                                                                         (1)

 

dove:

·                                   è il salto di entalpia

·                                            è la portata in massa (da ricavare)

·                       è il calore specifico dell’acqua

 

Per risolvere la 1) bisogna calcolare la portata in massa del sistema:

 

                                                                                                           (2)

 

dove

 

·          r                                    è la densità dell’acqua

·          W                       è la velocità del fluido (da determinare)

·          A                        è l’area della sezione del condotto

 

Bisogna distinguere due diverse densità per il fluido del sistema poiché esso si trova a due temperature diverse:

 

·          r1           relativo al tratto A (vedi figura pag. 11) a temperatura T1

·          r2           relativo al tratto B (vedi figura pag. 11) a temperatura T2

 

Dalle tabelle del vapore si estraggono i valori del volume specifico dell’acqua alle diverse temperature, da cui si ricavano le densità:

 

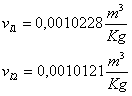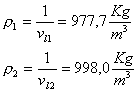        à        à                                  (3)

 

verrà anche utilizzato un valore di densità medio:

 

                                                                                                         (4)

 

Per andare avanti con il problema bisogna calcolare la velocità che compare nel punto 2); il problema si risolve dividendo il circuito in due tratte:

 

·          tratto A                 dalla caldaia al termosifone, a cui è  associata l’equazione 5)

·          tratto B                 dal termosifone alla caldaia, a cui è  associata l’equazione 6)

 

                                                                    (5)

                                                                     (6)

 

Esplicitando (P2-P1) dalla 5) , (P1-P2) dalla 6) e sommando membro a membro si ottiene:

 

                                      (7)

 

Per le scelte delle sezioni adottate e considerando che la differenza tra le densità r1 e r2 è piccola, si può trascurare il primo termine del secondo membro della 7), mentre, non si può trascurare il secondo termine, poiché esso rappresenta il motore dell’impianto.

Inoltre, davanti agli addendi che rappresentano le perdite di carico, viene sostituita la densità media r in modo da semplificare i calcoli; così facendo, la 7) diventa:

 

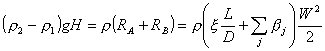                                            (8)

 

Da quest’ultima equazione si può ricavare la velocità da andare a sostituire nella 2) per il calcolo della portata in massa (che serviva nella (1) per soddisfare la richiesta del problema) ma, si nota che si tratta di un’equazione in due incognite (W e x). Ancora una volta per risolvere il quesito si deve intraprendere un procedimento ricorsivo; a tale scopo si fissa una velocità di primo tentativo per eseguire il seguente ciclo:

 

1.      calcolo (ipotesi se è il primo valore) della nuova velocità W’

2.      calcolo del numero di Reynolds (utilizzando il punto 1)

3.      calcolo del fattore di attrito (utilizzando il punto 2 e la scabrezza relativa)

4.      ritornare al punto 1.

 

Primo ciclo

Si ipotizza una velocità sensata e si calcola il numero di Reynolds corrispondente:

 

                                                        (9)

 

Utilizzando il diagramma di Moody, il valore della scabrezza relativa del condotto e la 9) si ricava il fattore d’attrito:

 

                                                                                                                      (10)

 

avendo utilizzato un valore di scabrezza relativa pari a:

 

                                                                                         (11)

 

Con il risultato dell’equazione 10) si riparte dal punto 1. del ciclo.

I risultati di qualche iterazione sono riportati nella tabella seguente.

 

W

Re

x

W’

0,5

44706

0,027

0,344

0,344

30758

0,028

0,342

0,342

30558

0,028

0,342

 

Dopo pochi cicli la velocità si stabilisce intorno al un valore che viene utilizzato per calcolare la portata in massa del sistema:

 

                                                      (13)

 

Infine, per la 1), la potenza termica cercata è:

 

                                   (14)

 

Utilizzando l’equazione 13) e l’equazione 14) si vede che se si dispone di condotti a sezioni piccole ci sarà bisogno di differenze di temperature più elevate per ottenere gli stessi risultati in termini di potenza termica.