Mora Marco matr. 131642; lezione del 27/11/2001 ore: 16.30 – 18.30
TECNICHE DI MISURA DELLA RISPOSTA AD IMPULSO
Le tecniche di misura avanzate della risposta ad impulso si basano su misure elettroacustiche; per analizzarle però vi sono diversi modi che andremo di seguito ad osservare.
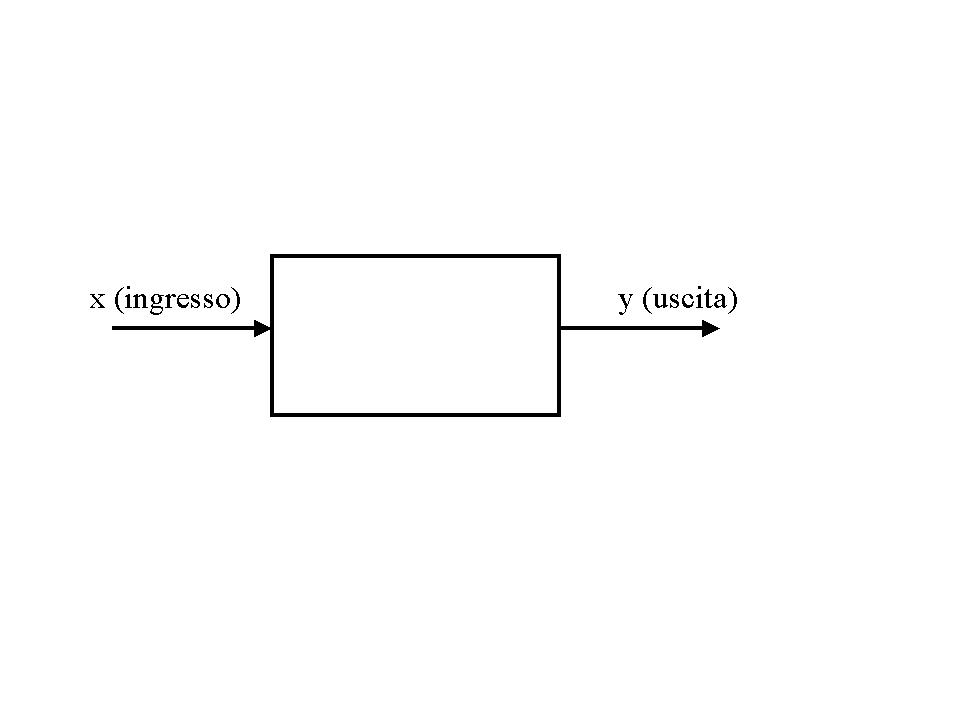
In senso lato è possibile definire SISTEMA un qualunque dispositivo, o interconnessione di dispositivi, o apparato, che produce un segnale di USCITA misurabile in corrispondenza a un segnale di INGRESSO noto. Quindi d’ora in avanti considereremo un sistema come un ambiente che ad un ingresso x(t) fa corrispondere un ben determinato ed unico segnale d’uscita x(t), ed una sua rappresentazione grafica può essere:

Il nostro sistema deve verificare due proprietà:
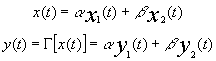
![]()
- INVARIANZA NEL TEMPO cioè ad un ingresso x(t – to) corrisponde un’uscita y(t – to). Questa relazione afferma che la risposta corrispondente all’eccitazione traslata nel tempo x(t – to) ha lo stesso andamento della risposta al segnale originario x(t) non traslato, purché la si trasli della stessa medesima quantità to:
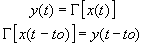
Preso un SLI ( sistema lineare a tempo invariante ) possiamo misurare la sua RISPOSTA IMPULSIVA, che è l’uscita del sistema in corrispondenza dell’eccitazione x(t) = δ(t) dove δ(t) θ la DELTA DI DIRAC. Indicando convenzionalmente la risposta impulsiva con h(t); introducendo il concetto di CONVOLUZIONE come un’operazione matematica chiamata integrale di convoluzione, identificata dal simbolo ![]() , che risponde alla seguente legge:
, che risponde alla seguente legge:
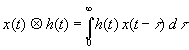
Possiamo ricavare la relazione fondamentale:
![]()
Il segnale di uscita può essere calcolato attraverso la convoluzione del segnale d’ingresso con la risposta impulsiva.
Fino ad ora abbiamo assunto i segnali di ingresso e di uscita essere segnali a tempo continuo, in realtà, la tendenza è quella di lavorare su segnali a tempo discreto.
Un segnale a tempo discreto si può ottenere da un segnale a tempo continuo, mediante l’operazione di campionamento.
Un enunciato matematico, che va sotto il nome di teorema del campionamento, dice che qualunque forma d’onda costituita da più componenti di frequenze diverse può essere descritta esattamente da una successione di numeri che danno il valore dell’ampiezza della forma d’onda a intervalli determinati dalla larghezza di banda della forma d’onda stessa, cioè dalla gamma delle frequenze componenti (convenzionalmente espresse in hertz, ovvero cicli al secondo). Specificatamente, la frequenza di campionamento (la velocità con cui debbono essere generati i numeri) deve essere uguale al doppio della larghezza di banda della forma d’onda.
Cioè il campionamento consiste nell’estrarre dal segnale stesso i valori che esso assume a istanti temporali equispaziati, multipli di un intervallo T detto PERIODO DI CAMPOINAMENTO. Tali valori andranno quindi a costituire una sequenza il cui valore n-esimo è il valore assunto dal segnale a tempo continuo all’istante nT.
Naturalmente lavorando con segnali a tempo discreto cambiano le operazioni matematiche alla base; in particolare consideriamo la convoluzione, che per segnali campionati, diventa:
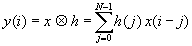
Ora il nostro problema è quello di passare dal dominio del tempo a quello delle frequenze. Per questo motivo introduciamo la TRASFORMATA DI FOURIER (FT), infatti invece di considerare il segnale a tempo discreto vero e proprio x(n) consideriamo la sua trasformata di Fourier X(f):
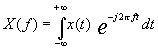
ed indicheremo l’operazione di trasformata nel modo seguente
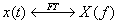 La ragione principale di tutto ciò è che in ambito frequenziale vale il cosiddetto
La ragione principale di tutto ciò è che in ambito frequenziale vale il cosiddetto
teorema della convoluzione, che afferma che convolvere due segnali in ambito temporale è equivalente a fare il prodotto delle trasformate di Fourier dei due segnali, nel dominio delle frequenze.
![]()
Se quindi ripensiamo alla tendenza moderna ad implementare tali operazioni mediante DSP, ci rendiamo conto dell’importanza di ridurre il costo di calcolo delle operazioni che ci sono necessarie.
Quindi se consideriamo vari algoritmi efficienti come per esempio l’FFT (Fast Fourier Transform)ed il suo algoritmo inverso IFFT che è la trasformata veloce di Fourier inversa, otteniamo:
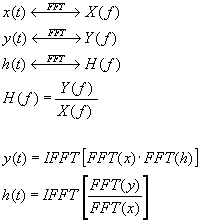
Questa relazione, afferma che applicando un segnale x(t) al nostro ambiente e misurando il segnale di uscita y(t), per calcolare la risposta all’impulso è sufficiente applicare ai segnali x(t) e y(t) la trasformata di Fourier ottenendo così X(f) e Y(f) il cui rapporto ci da H(f), che usualmente viene chiamata FUNZIONE DI TRASFERIMENTO, e che non è altro che la trasformata di h(t); applicando quindi l’operazione di trasformata inversa da H(f) otteniamo la nostra risposta all’impulso cercata.
APPLICAZIONI REALI
Il motivo per cui oggi si preferisce lavorare su segnali digitali, cioè a tempo discreto, è la facilità con la quale si possono elaborare mediante microprocessori specializzati, chiamati DSP (Digital Signal Processor).
Il primo passo nella registrazione digitale è la digitalizzazione di un segnale audio. Il dispositivo che svolge questa funzione prende il nome di convertitore analogico-digitale o ADC ( da analogue-to-digital converter). La forma d’onda di un segnale analogico è una funzione bidimensionale (dà l’ampiezza del segnale in funzione del tempo), e pertanto si deve predisporre un segnale digitale che descriva con precisione ambedue le dimensioni.
In primo luogo, il segnale viene campionato a intervalli regolari determinati da una frequenza di campionamento standardizzata; i dati poi sono raccolti a una velocità predeterminata. Quando viene il momento di ricostruire i dati sotto forma di segnale analogico, l’informazione deve essere restituita esattamente alla stessa frequenza per evitare variazioni di velocità o di altezza del suono.
La tensione che rappresenta l’ampiezza del segnale al momento della conversione viene poi memorizzata in modo analogico per un tempo abbastanza lungo da consentire la misurazione e l’assegnazione di un numero che rappresenta il valore di tensione. Questo passo prende il nome di quantizzazione. Ogni campione genera un nuovo numero: così si forma un flusso di dati che può essere elaborato da qualunque sistema digitale.
Al fine di ricostruire il segnale, i dati sono presentati a un convertitore digitale-analogico o DAC (da digital-to-analogue converter) alla frequenza di campionamento. Il convertitore genera una tensione che rappresenta il valore dei dati e conserva la tensione fino a che non riceve una nuova parola di dati. Il segnale risultante è una replica della forma d’onda originale.
Una volta registrato il nostro segnale vi sono vari modi per memorizzare i dati ottenuti dal campionamento; uno dei più comodi ed usati è il Compact Disc o CD.
I dati digitali sono memorizzati originariamente sotto forma di una serie di cavità, che rappresentano rispettivamente le cifre binarie 1 o 0. Si ha un 1 dove inizia o finisce una cavità, uno 0 là dove non vi è variazione. La superficie incisa è fusa in plastica da uno stampo ottenuto da una matrice: le cavità quindi diventano piccoli rilievi. La superficie del disco è alluminata per conferirle riflettività (il dispositivo di riproduzione è un fascio laser) e protetta da uno strato di plastica trasparente.
Quando il disco viene riprodotto, il fascio laser va a colpire o un’area piana o un rilievo. Se incide su un’area piana, viene riflesso verso un fotorivelatore. Se incide su un rilievo, viene diffuso. Il sensore registra una variazione di intensità come un 1, la mancanza di variazione come uno 0. E’ evidente che la superficie del disco deve rimanere sufficientemente piana e il sistema ottico sufficientemente stabile perché la distanza fra l’obbiettivo del sistema ottico del laser e il disco non cambi. In caso contrario il fascio non sarà più ben focalizzato e andrà a investire un’area maggiore di quella che corrisponde a un singolo bit.
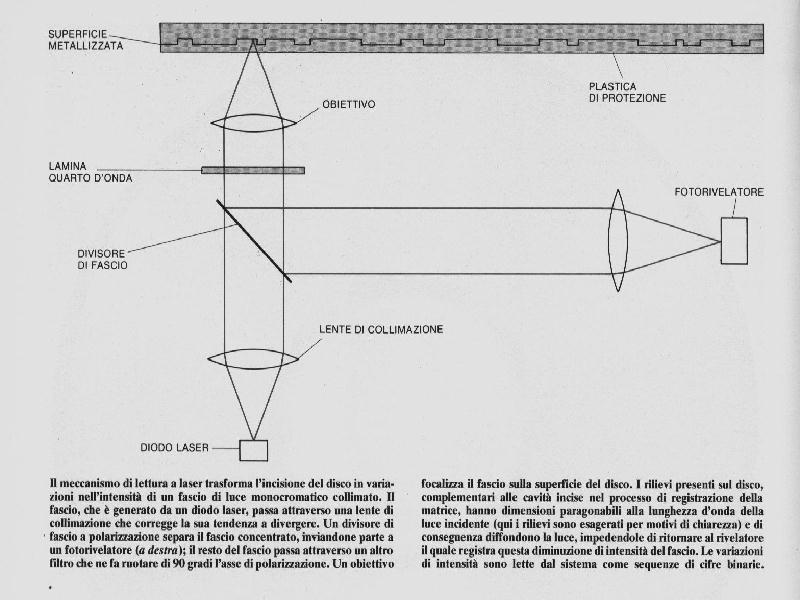
Schema di lettura e funzionamento di un CD
PROBLEMATICHE
L’utilizzo di un segnale del genere è possibile purché il segnale x d’ingresso abbia uno spettro che copra tutte le frequenze, quindi una serie di campioni sufficientemente lunghi. Infatti l’utilizzo di un segnale statico di diffusione di energia nelle frequenze a noi scomode richiede un tempo di registrazione molto lungo (esempio il parlato o una canzonetta musicale ).
Quindi c’è da cercare di usare segnali alla stessa energia a tutte le frequenze, il caso più banale è il RUMORE BIANCO, in modo da rendere minimo il tempo di misura.
Un altro problema è che si deve usare una FFT di lunghezza adeguata al tempo di risposta del sistema. infatti, come detto prima, si deve ripetere il segnale nel tempo per ottenere dati per la media e usare una frequenza di ripristino che non porti sovrapposizioni dei segnali in uscita ed inoltre una FFT che comprenda ogni volta la risposta all’impulso di una singola ripetizione; altrimenti si verifica il fenomeno del TIME ALIASING.
SEGNALE MLS
Per ovviare a questa serie di problemi si può usare in ingresso un segnale che prende il nome di MLS (Mximum Length Sequence).
Questa tecnica, inventata nel 1975 dal tedesco Alrutz, è stata una delle più usate; grazie alla diffusione di una scheda, costruita nel 1989 dall’americano Douglas Rife, che implementava per via hardware lo shift registrer e corredata da un software chiamato MLSSA (melissa) particolarmente potente, tanto da essere tuttora usato.
Questo segnale è una sequenza binaria costruita tramite uno Shift register (registro a scorrimento):
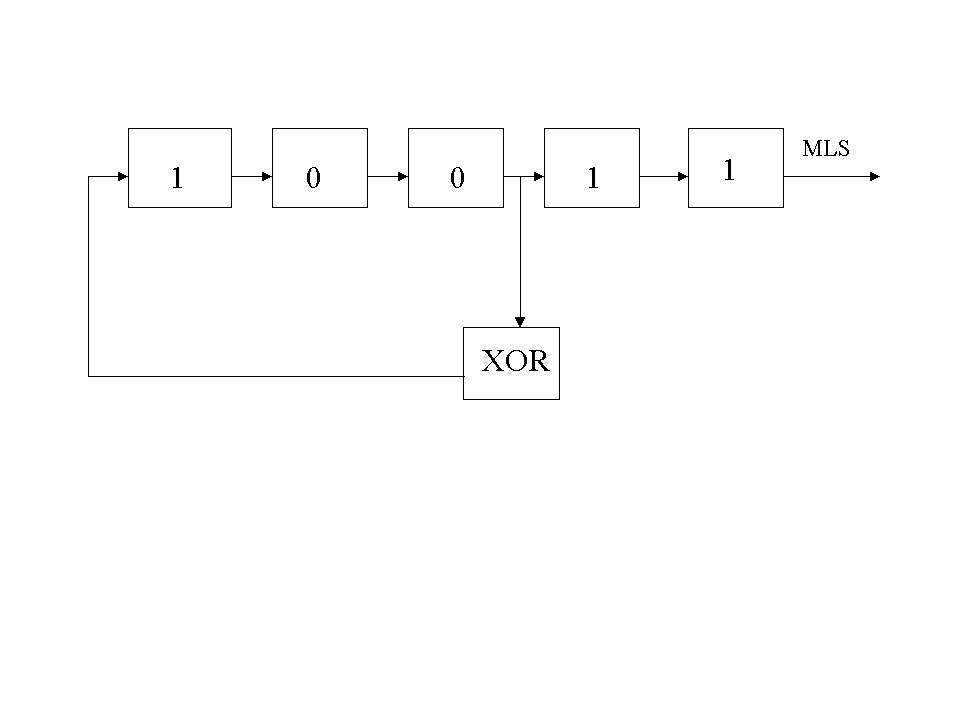 Esempio di Shift register a 5 bit, i numeri scorrono a destra ad ogni passo.
Esempio di Shift register a 5 bit, i numeri scorrono a destra ad ogni passo.
In questo modo il segnale che esce è una sorta di onda quadra, che varia unicamente per l’ampiezza.
Con opportuni valori iniziali e un corretto posizionamento dell'xor si ottiene un MLS.
Si possono fare varie osservazioni su questa sequenza:
· essendo nota in partenza si trova matematicamente MLS -1 con l’inversione di Hadamard; essendo inoltre MLS -1 un segnale binario è particolarmente facile la convoluzione (poiché spariscono le moltiplicazioni)
· grazie alla semplicità di questo segnale è possibile fare la convoluzione nel dominio dei tempi in tempo reale
· siccome il segnale in entrata è generato direttamente non deve più essere campionato e quindi si può usare una scheda di campionamento ad una sola entrata
· inoltre essendo lo spettro sonoro dell’MLS piatto come quello del rumore posso fare anche l’analisi in frequenza.
Si dimostra che la lunghezza di una MLS è di 2n - 1 dove n è il numero di celle dello shift register. In acustica in particolare, si usano normalmente shift registers a 16 o più celle ricavando MLS di 65535 campioni (caso 16 celle) o superiori (ovviamente però si può ripetere il segnale).
Gli svantaggi di questa tecnica sono la fortissima dipendenza dalle caratteristiche di linearità del sistema. Infatti nel caso di non-linearitá anche lievi possono apparire echi inesistenti e si può avere la cancellazione delle alte frequenze a causa del loro sfasamento reciproco che le può portare in controfase. Purtroppo quindi questa tecnica può essere usata solo con riproduttori audio molto fedeli e per un tempo non troppo lungo, infatti il riscaldamento degli altoparlanti comporta una perdita di fedeltà e conseguentemente di linearità.
ANALISI PRATICA
Descrizione dell’impianto di misura:
Per effettuare le misure è necessario avere: un computer dotato di scheda audio full duplex (ovvero abilitata a registrare da un canale mentre riproduce su di un altro), un software di hard disk recording funzionante in modalità multitraccia (Cool Edit pro oppure Cakewalk Pro Audio o altri), un impianto di riproduzione ed un microfono. Il microfono da noi usato è un SOUND FIELD MICROPHONE che è dotato di quattro capsule microfoniche, quindi in grado di misurare il segnale di compressione w, ma anche le tre componenti cartesiane della velocità x, y, z.
Il software funge sia da riproduttore del segnale di eccitazione sia da registratore del segnale di risposta dell’ambiente; questo fa nascere la necessità di un computer che supporti il full duplex.
L’impianto è molto semplice, infatti all’uscita della scheda audio si collega l’impianto di riproduzione (nel mio caso due speaker da concerto amplificati con un amplificatore esterno) e all’entrata di registrazione della scheda audio si collega il microfono (che se passivo potrebbe necessitare di una preamplificazione).Collegato l’impianto si procede a fare le misure.
Prime misure con MLS
Una possibilità è quella di generare un segnale di eccitazione con la tecnica MLS grazie ai plug-in AURORA utilizzabili nell’ambiente di Cool Edit.
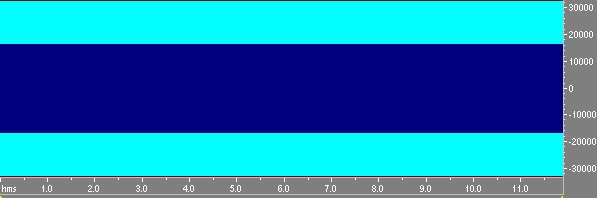
Fig. 1 Segnale MLS multiplo di ordine 16 ripetuto 8 volte.
Come si può vedere dall’analisi delle frequenze. questo segnale è molto simile al rumore bianco.
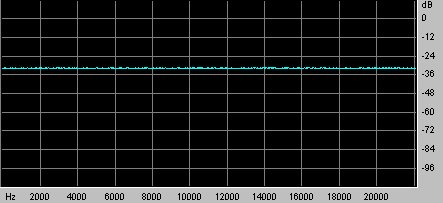
Fig 2 Spettro dell'MLS visto con Cool Edit
Ora si può procedere ad una misura: in Cakewalk la prima traccia contiene il segnale MLS mentre la seconda registra simultaneamente la risposta dal microfono.
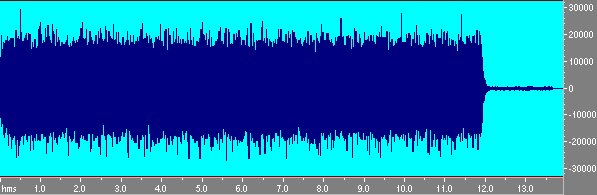
Fig. 3 Segnale di risposta registrato con il microfono.
Ora per ottenere la risposta della stanza alla δ si deve deconvolvere il file di risposta con l’inverso della MLS. Per fare questo si usa la funzione deconvolve multiple MLS di AURORA. Il risultato θ un’onda che rappresenta la risposta dell’ambiente alla δ di Dirac. Il risultato della deconvoluzione, mostrato in figura 4, si trova nella clipboard di Windows.
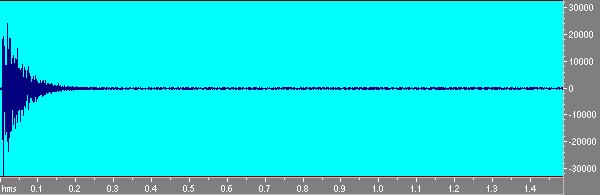
Fig 4 Risposta della stanza ottenuta con MLS.
Notiamo che nella deconvoluzione bisogna usare un filtro che rimuova la componente continua, già integrato nel plug-in che deconvolve.
SEGNALE SWEEP
Attualmente, comunque, la tecnica migliore è quella dello sweep. Il segnale così definito è composto da un seno che parte dalle frequenze basse e sale verso l’alto.
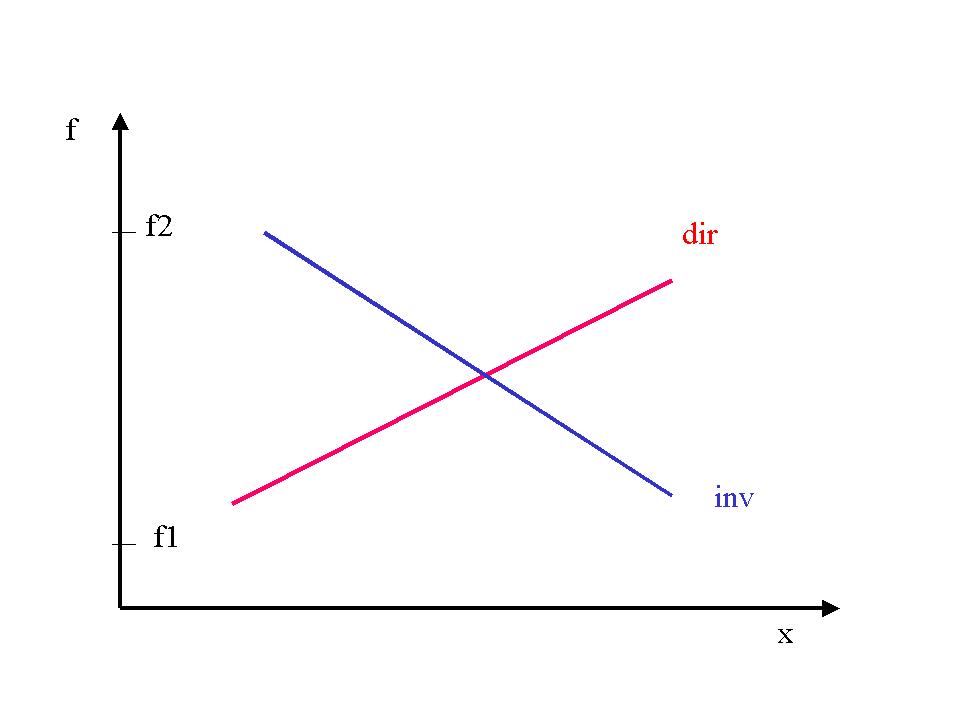
In base al tipo di relazione che governa la crescita della frequenza si possono distinguere segnali
Sine Sweep di tipo Lineare o Logaritmico.
Se si usa una sinusoide con sweeppaggio di tipo lineare si ha un grafico delle frequenze come quello sotto; che equivale ad uno spettro di un segnale bianco.
 Il segnale veniva fatto passare attraverso un Filtro Inseguitore.
Il segnale veniva fatto passare attraverso un Filtro Inseguitore.
Generalmente la preferenza ricade sui segnali di tipo logaritmico perché questi hanno il pregio di fornire più energia nella regione delle basse frequenze, che rappresenta una zona critica, e di procedere più speditamente nella regione delle alte frequenze. Inoltre lo spettro di un segnale Sine Sweep logaritmico assomiglia molto a quello di un rumore rosa, ed ha quindi il vantaggio di essere più gradevole all’ascolto rispetto al rumore bianco.
Osserviamo, inoltre che i segnali Sine Sweep hanno una interessante caratteristica: l’inversione di questo tipo di segnale è lo stesso segnale invertito sull’asse dei tempi, secondo la tecnica Time Reversal Mirror.
L’unica controindicazione nell’impiego di questo segnale è la potenza di calcolo che esso richiede. L’operazione di convoluzione, infatti, non trae nessun vantaggio dall’utilizzo di questo segnale, e presenta quindi la ben nota complessità di calcolo.
Va inoltre detto che passando nel dominio delle frequenze per effettuare l’operazione di convoluzione si può ricorrere all’algoritmo Overlap And Save che permette di lavorare su un numero di campioni dell’ordine di centinaia di migliaia.
Un altro utile utilizzo di Cool Edit è la simulazione di ambienti particolari; per esempio è possibile provare l’acustica di un teatro in fase di progettazione, ancor prima di costruirlo.
Misure con la tecnica Sweep
Una seconda possibilità è quella dello sweep: ovvero un segnale composto da un tono puro la cui frequenza si alza nel tempo.
In questo caso si genera sempre mediante AURORA un segnale composto da tre sweep logaritmici con frequenze che partono da 100 hz ed arrivano a 20000 hz separati da 1 secondo di silenzio ognuno.
Lo sweep usato è logaritmico (la frequenza sale nel tempo in maniera logaritmica) perché in questo modo si dà più energia alle basse frequenze (zona critica) e si procede più svelti sulle alte in modo da non bruciare i tweeter. In figura 5 si vede il sonogramma (rappresentazione tempo-frequenza) del segnale sweep
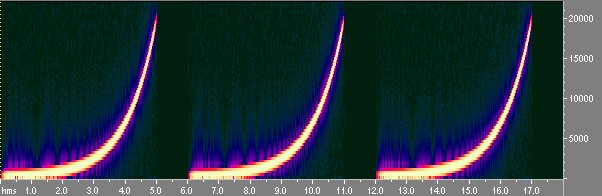
Fig 5 Sequenza di tre sweep vista con Cool Edit spectral view
Le zone più chiare indicano maggiore energia del segnale: come si vede la variazione di frequenza è logaritmica. Si fa la misura come in precedenza e si ottiene la risposta della stanza allo sweep di fig. 6:
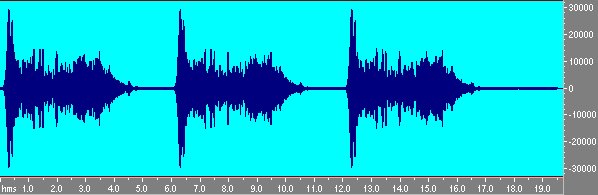
Fig 6 Risposta alla sequenza di tre sweep.
Ora bisogna convolvere con lo sweep inverso, che il plug-in di generazione dello sweep ha già posto nella clipboard.
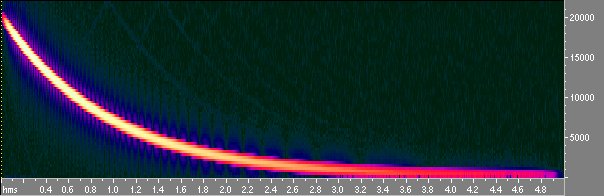
Fig 7 Sweep inverso visto con Cool Edit spectral view
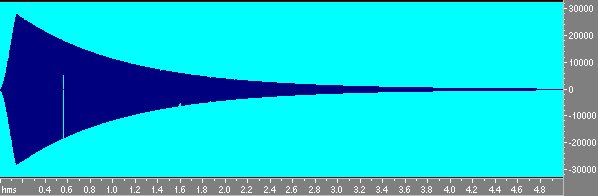
Fig 8 Sweep inverso visto come ampiezza-tempo.
Notiamo che mentre lo sweep diretto ha ampiezza costante lo sweep inverso è calante in ampiezza in modo da compensare la logaritmicità dello sweep che dava più energia alle basse frequenze. Infatti lo sweep logaritmico ha energia crescente di 3 db per ottava e quindi è un rumore rosa, se si convolve questo segnale con sé stesso non si ottiene la d di Dirac ma un segnale che va giù di 6 db per ottava. Questo viene compensato dal guadagno variabile dell’inverso. Convolvendo lo sweep col suo inverso si ottiene invece la δ di Dirac; osservando attentamente si nota perσ che non è esattamente la δ ma un filtro passabanda da 100 hz a 20000 hz. Questo perché la banda passante non arriva alla frequenza di Nyquist ma si ferma a 20000.
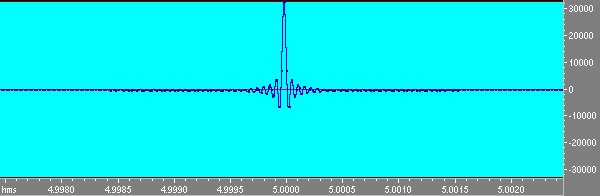
Fig 9 δ di Dirac ottenuta dallo sweep.
Convolvendo invece il segnale di risposta della stanza con lo sweep inverso otteniamo la risposta della stanza. Notiamo intanto che avendo tre sweep si hanno anche tre risposte che è possibile mediare fra loro ed inoltre come queste tre risposte siano assai simili a quella ottenuta con la tecnica MLS, ma molto più pulite. In fig. 10 la risposta dell’ambiente ottenuta con lo sweep.
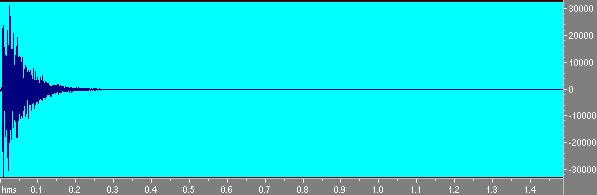
Fig 10 Risposta della stanza ottenuta da sweep e mediata.