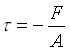
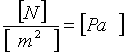 (1)
(1)
Fluidodinamica
Indice:
Generalità
Un liquido può scorrere sia dentro che fuori ad un determinato corpo: nel primo caso si parla di MOTO INTERNO, nel secondo caso di MOTO ESTERNO.
1)
Nel moto interno calcoliamo le cadute di pressione che avvengono tra due sezioni del corpo attraversato dal fluido: tali perdite sono chiamate PERDITE DI CARICO .La scienza che si occupa di ciò è l’idraulica e studia in particolare il moto dei fluidi incomprimibili (il fluido, oltre che liquido può essere anche gassoso,in quanto considero la densità costante).2)
Nel moto esterno calcoliamo invece la risultante delle forze che viene prodotta dall’interazione fluido-struttura: che sia il fluido a muoversi ed il corpo fermo o viceversa non ha importanza in quanto considero il moto relativo tra un corpo solido ed un fluido (es. missile,automobile,vento che investe un edificio).Ci interessa dunque ricavare la cosiddetta FORZA DI TRASCINAMENTO.Le equazioni che governano questi problemi sono sostanzialmente le stesse,anche se chiaramente applicandole alle due diverse situazioni porteranno a risultati leggermente diversi.
Viscosità e aderenza
La VISCOSITA’ è l’insieme delle forze tangenziali tra superficie e fluido e tra strati di fluido diversi che si oppone al moto del fluido stesso rispetto alla superficie. Queste forze tangenziali sono dette TENSIONI (t ) e hanno la forma del tipo:
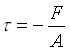
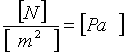 (1)
(1)
dove F è la forza che agisce su un elemento di area A che si oppone al verso del movimento del liquido.
Prendiamo un fluido in moto relativo rispetto ad una superficie solida: se tracciamo in un dato istante un segmento colorato normale alla superficie, e se dopo un intervallo di tempo si fotografa ancora la porzione di liquido considerato, si nota che in breve tempo tale segmento si è deformato nel senso del moto, dando luogo ad una curva che rappresenta la variazione della velocità del fluido al variare della distanza dalla superficie solida in quiete (fig.1).La particella colorata a contatto con la superficie solida non si è spostata, ha avuto cioè velocità nulla, verificando così il fenomeno dell’ADERENZA.
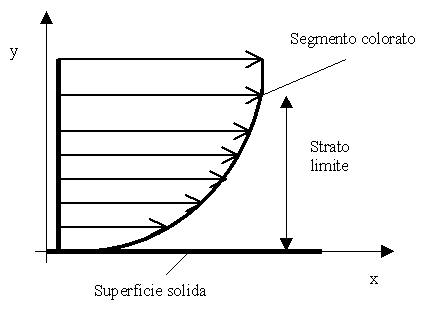
Fig.1: profilo di velocità di un fluido e strato limite
La porzione di fluido all’interno del quale il fluido subisce la variazione di velocità,è detta STRATO LIMITE.
Un fluido che investe un determinato corpo non solo produce tensioni tangenziali ( t ) dovute alla viscosità, ma anche forze normali dovute alla pressione ( p) prodotte dalle particelle del fluido (fig.2).
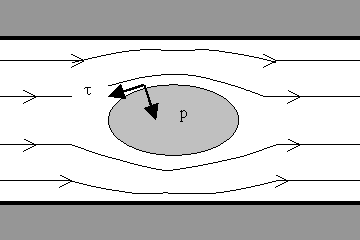
Fig.2: forze tangenziali e normali agenti sul corpo per effetto del movimento del fluido
Resistenza al moto di un corpo in un fluido
Il problema della forza esercitata da un fluido viscoso su un corpo in esso immerso è complesso. George Stokes, nel 1845, prese in considerazione il problema solo per un caso particolare, quello di un oggetto di forma sferica, completamente immerso in un fluido in moto laminare, di densità costante ed incomprimibile. Per questa situazione egli ricavò che il modulo della forza di attrito che agisce sul corpo si esprime come: Fr = -6p
h
rv
detta legge di Stokes. In questa formula Fr è il modulo della forza ritardante, h
è il coefficiente di viscosità del fluido, r è il raggio della sfera e v il modulo della velocità della sfera rispetto il fluido.
La formula sia stata ricavata per un oggetto di forma sferica essa può essere applicata in molte situazioni (cambierà il valore delle costanti di proporzionalità): dai fenomeni meteorologici alle particelle in sospensione in un fluido.
Verifichiamo la plausibilità di questa formula attraverso l'analisi dimensionale: è ragionevole supporre che la forza ritardante agente sul corpo immerso nella corrente fluida sia proporzionale ad una qualche potenza della viscosità, del raggio della sfera e della velocità, e che sia tale da opporsi alla direzione del moto.
Per il modulo di questa forza possiamo allora scrivere: Fr = kh arbvc
Riducendo le quantità elencate alle dimensioni fondamentali si ha:
M L T-2 = (M L-1 T-1)a Lb (L T-1)c
Imponendo la coerenza dimensionale dei fattori corrispondenti nei due membri si ha:
|
1 = a |
|
|
per L |
1 = - a + b + c |
|
per T |
- 2 = - a - c |
sistema che risolto dà a = 1, b = 1 e c = 1, proprio come nell'equazione sopra, posto il coefficiente k = 6p .
Se il moto invece è turbolento le forze inerziali dominano su quelle viscose e la forza di resistenza è: Fr = -1/2 cr
Av2
Infatti se consideriamo un cilindro di fluido con immersa in esso una sfera di sezione A e immaginiamo che il fluido che entra a contatto con la sfera perda mediamente metà della propria quantità di moto nella direzione di avanzamento, poiché la massa che nell'unità di tempo subisce una perdita di velocità pari a 1/2 v è (r vA) , la forza di reazione inerziale che agisce sulla sfera è proporzionale a (1/2 r v² A). La costante c che compare nella formula sopra è chiamata coefficiente di resistenza.
Legge di Newton
Tale legge sancisce la proporzionalità lineare tra la tensione tangenziale t e la derivata parziale della velocità u del fluido rispetto ad y tramite la viscosità m :
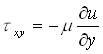 (2)
(2)
t : tensione che si esercita nella direzione (x) sulla superficie normale ad (y) rivolta verso le (y) decrescenti (è opposta al verso del moto e quindi ho il segno – nella formula).
u : è la velocità
m : costante di viscosità propria di ogni fluido,è un numero puro e si misura in
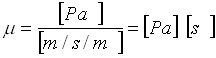
La (2) fu enunciata con la specificazione y=0, descrivendo così la forza reciproca tra parete solida e fluido in moto;il fluido "tira" la parete verso destra con uno sforzo t e la parete frena il fluido con uno sforzo uguale e contrario (fig.3). Tuttavia la legge vale anche se non ho la parete solida in quanto all’interno di un fluido,lo strato che scorre ad una velocità superiore di quella dello strato confinante esercita una forza di trascinamento sullo strato più lento e quest’ultimo esercita una forza uguale e contraria di frenaggio sullo strato più veloce,continuando così a valere il bilancio delle forze.
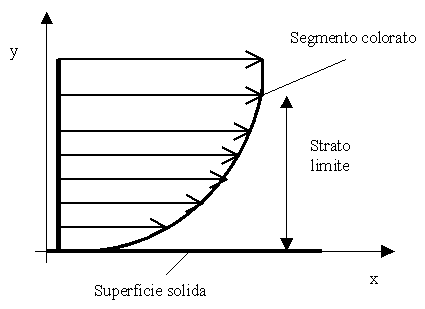
Fig.3:forza di trascinamento(verso destra) e forza di frenaggio(verso sinistra) tra fluido ed acqua.
Oltre a m , chiamata VISCOSITA’ DINAMICA, esiste anche la VISCOSITA’ CINEMATICA n , definita come:
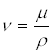
![]() (3)
(3)
dove r è la densità del fluido.
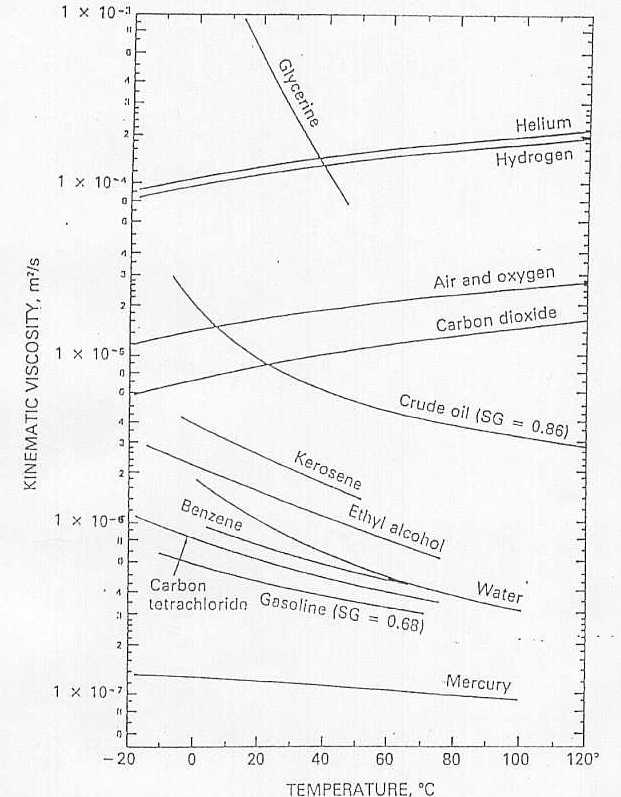
Dalle unità di misura si nota che m è una tensione mentre n no; non bisogna confonderle in quanto solo nel caso dell’acqua esse sono circa uguali ( r dell’acqua è 1) mentre in tutti gli altri casi sono molto diverse!!!(vedere le 2 tabelle alla fine in fondo).
Dunque secondo la legge di Newton, il comportamento di un fluido è caratterizzabile dalla viscosità che non è costante, bensì varia al variare della temperatura. Tale legge, come tutte le leggi, non è esatta, è solo un’approssimazione della realtà, ed in particolare è valida solo per acqua ed aria, mentre tutti gli altri fluidi deviano da questa legge.
Il coefficiente di viscosità
Prendiamo un fluido confinato tra due lastre parallele di area A e distanti tra loro z. Teniamo ferma la lastra inferiore e facciamo scorrere quella superiore con una velocità costante v applicandovi una forza F (fig. 4):
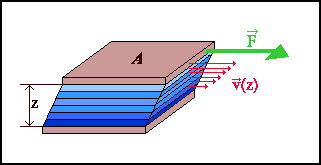
Fig4: strati di fluido in movimento
Tale forza è necessaria perché il fluido vicino alla lastra superiore esercita su essa una resistenza viscosa che si oppone al moto : ogni strato di fluido esercita su quelli adiacenti ad esso una forza resistente dimodoché la velocità del fluido vicino alla lastra alla quale è applicata la forza è v mentre è quasi nulla vicino alla lastra inferiore, variando linearmente con la quota.
Il modulo della forza F risulta direttamente proporzionale a v e ad A ed inversamente proporzionale alla distanza z tra le lastre attraverso un coefficiente di proporzionalità h
detto coefficiente di viscosità: F= h
(va) /z
Viscosimetro a rotazione
Lo strumento migliore per studiare la viscosità di un fluido è il VISCOSIMETRO A ROTAZIONE. E’ costituito da un motorino elettrico, da cui esce un piccolo albero, alla base del quale si trova un cilindretto chiamato ROTORE o EQUIPAGGIO MOBILE. Il motorino imprime all’albero una rotazione di una certa velocità angolare; immergo ora il cilindretto in una tazza cava di forma cilindrica (fig.5). Tra i due cilindri, entrambi di acciaio inox, scorre del liquido ( in genere acqua).Pongo in rotazione con velocità angolare costante w il cilindro esterno: con il passare del tempo, notiamo dapprima mettersi in rotazione gli strati più esterni del fluido e successivamente quelli via via più interni fino a che entra in rotazione anche il cilindro interno.
Questo processo può intervenire soltanto se in seno al fluido nascono degli sforzi diretti tangenzialmente al moto e quindi in grado di trascinare i successivi strati di fluido ed anche il cilindro interno, trasmettendo la coppia applicata al cilindro esterno per mantenerlo in rotazione.
Se voglio mantenere in quiete il cilindro interno, occorre applicarvi una coppia resistente a mezzo, per esempio, di una forza tangenziale t
. Notiamo allora che la velocità del fluido alla parete del cilindro esterno è w
r![]() , mentre è nulla alla parete del cilindro interno; questo indica che alle pareti il fluido si muove con la stessa velocità di queste e cioè non esiste slittamento tra pareti e fluido. Consideriamo ora un generico cilindro di raggio r (
, mentre è nulla alla parete del cilindro interno; questo indica che alle pareti il fluido si muove con la stessa velocità di queste e cioè non esiste slittamento tra pareti e fluido. Consideriamo ora un generico cilindro di raggio r (![]() <
< ![]() ): il fluido che si trova all’esterno di questa superficie per poter far muovere quello posto all’interno, deve esercitare sulla superficie stessa un’azione di trascinamento risultante da sforzi diretti, in ogni punto, tangenzialmente al moto nello stesso verso della velocità; un’azione identica ma di verso opposto viene esercitata dal fluido interno su quello esterno, che risulta perciò frenato nel suo movimento.
): il fluido che si trova all’esterno di questa superficie per poter far muovere quello posto all’interno, deve esercitare sulla superficie stessa un’azione di trascinamento risultante da sforzi diretti, in ogni punto, tangenzialmente al moto nello stesso verso della velocità; un’azione identica ma di verso opposto viene esercitata dal fluido interno su quello esterno, che risulta perciò frenato nel suo movimento.
Quando l’intercapedine tra i due cilindri è molto piccola rispetto ai loro raggi, cosicché si possa ritenere che la velocità del fluido vari linearmente fra le due pareti solide, le esperienze condotte nelle più svariate condizioni ( variando i raggi o la velocità angolare w
) mostrano che lo sforzo tangenziale t
è direttamente proporzionale alla differenza di velocità ![]() e inversamente proporzionale alla distanza
e inversamente proporzionale alla distanza ![]() tra i due cilindri tramite la viscosità m
:
tra i due cilindri tramite la viscosità m
:
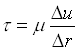 (4)
(4)
Il motore è dotato di una cella di coppia che misura il momento M e la velocità angolare v .La prova che faccio consiste dunque nel far variare progressivamente la velocità di rotazione all’interno della tazza partendo da valori molto bassi e aumentandola mano a mano, misurando in corrispondenza di ogni velocità il momento. Il momento è espresso come:
M=t
s r![]() (5)
(5)
Dove t
è la forza tangenziale, r![]() è il raggio del cilindretto interno ed s è la superficie laterale del cilindro.
è il raggio del cilindretto interno ed s è la superficie laterale del cilindro.
Dalla (2) e dalla (5) concludo quindi che c’è proporzionalità tra momento M e gradiente di velocità ![]() .
.
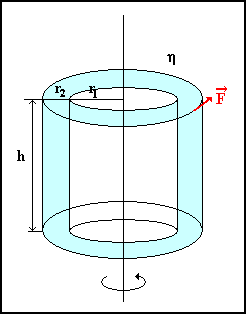
Fig.5:viscosimetro a rotazione costituito dal cilindretto interno di raggio r![]()
Tipi di fluidi
Per i gas e per la maggior parte e per la maggior parte dei liquidi a basso peso molecolare, si ha che m
dipende solo dalla natura del fluido e dal suo stato fisico; tali fluidi ubbidiscono perfettamente alla legge di Newton e sono quindi detti NEWTONIANI (es. acqua, benzina, butano) e sul grafico (fig.6) hanno un andamento lineare, con una pendenza data da 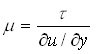 .
.
Esistono però molti fluidi che non seguono la legge di Newton in quanto m
risulta legato ad altre grandezze caratteristiche delle particolari condizioni sperimentali, oltre che al valore dello sforzo tangenziale t
![]() e al tempo. Per quanto riguarda la dipendenza dal valore dello sforzo, è possibile distinguere i fluidi NON NEWTONIANI in PSEUDUPLASTICI e DILATANTI:
e al tempo. Per quanto riguarda la dipendenza dal valore dello sforzo, è possibile distinguere i fluidi NON NEWTONIANI in PSEUDUPLASTICI e DILATANTI:
Pseudoplastici: tendono a smollarsi e il valore di m cala al crescere del gradiente di velocità ( es. fanghi, gelatine, polimeri liquidi come gomma o acetato di cellulosa).
Dilatanti: tendono ad indurirsi e il valore di m aumenta al crescere del gradiente di velocità ( es. grassi, sabbia in sospensione).
Una proprietà importante di questi fluidi è quella di avere memoria. Cioè dopo che ho smollato uno pseudoplastico, ovvero dopo che ne ho rotto una serie di legami interni che tenevano unite le particelle, esso tende a restare molle, avendo così memoria del passato. Se dunque torno indietro, non appena cala la velocità di deformazione, lo sforzo cala rapidamente e il fluido compie un cammino inverso a quello che ha fatto prima, seguendo un andamento ISTERETICO.
Ovviamente accade l’opposto per il materiale dilatante, che dopo che si è indurito tende a rimanere duro anche se riduco la velocità e segue anch’esso un ciclo isteretico.
Spesso quindi i dilatanti sono anche fluidi REOPEPTICI, cioè fluidi che una volta induriti, rimangono tali, presentando un aumento di m per effetto della lunga applicazione di uno sforzo tangenziale costante ( a temperatura costante) (es. impasti di gesso in acqua).Gli pseudoplastici invece, possono anche essere TIXOTROPICI, cioè fluidi che una volta ammolliti tendono a rimanere tali e presentano una diminuzione di m sempre per effetto dell’applicazione dello sforzo tangenziale (es. prodotti alimentari, vernici).
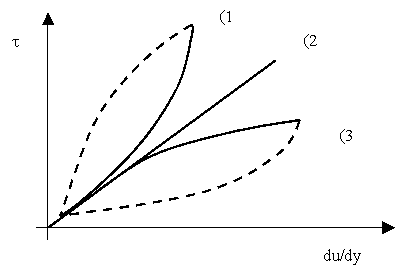
Fig.6:diagramma della viscosità dei fluidi 1)Dilatanti 2)Newtoniani 3)Pseudoplastici
Tale grafico prende il nome di CARATTERISTICA REOLOGICA DI UN FLUIDO.
Esistono inoltre dei fluidi particolari chiamati FLUIDI DI BINGHAM, che inizialmente si comportano da solidi e quindi fino ad un certo sforzo iniziale t
![]() non si deformano, poi, superato tale sforzo, iniziano la deformazione (es. vetro, maionese, burro).
non si deformano, poi, superato tale sforzo, iniziano la deformazione (es. vetro, maionese, burro).
Ipotesi di lavoro
Per formulare leggi che regolino il moto dei fluidi consideriamo un fluido ideale, cioè un fluido incomprimibile e non viscoso; consideriamo inoltre il caso che si muova di moto stazionario e irrotazionale.
Nel moto stazionario la velocità in ogni punto è costante nel tempo, cioè ogni particella che transita per un qualsiasi punto P lo fa sempre con v la stessa velocità in modulo e verso. Perciò se tracciamo il percorso di una particella, questo sarà anche il percorso di ogni altra particella che arriva in P : lo spazio occupato dalla corrente è quindi proprio un campo vettoriale.
La curva che descrive il moto della particella si chiama linea di flusso ed è tangente alla velocità della particella in ogni suo punto.
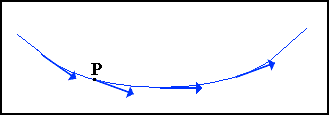
Fig. 7: linea di flusso
Nel moto stazionario le linee di flusso non si incrociano mai, in quanto se lo facessero una particella che arriva al punto di incrocio potrebbe proseguire lungo una linea o l'altra, quindi in uno stesso punto potrebbe avere differenti valori di velocità, contrariamente all'ipotesi stessa di stazionarietà.
È possibile quindi dire che per il moto stazionario esiste una sola linea di flusso per ogni punto del fluido e che l'insieme delle linee di flusso è fisso nel tempo. Prendendo un fascio di linee di flusso otteniamo una superficie tubolare detta tubo di flusso
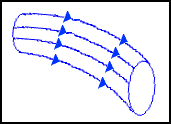
Fig.8:tubo di flusso
Per semplicità d'ora in avanti faremo coincidere il tubo di flusso con il condotto reale entro il quale scorre il fluido, ma teniamo presente la natura vettoriale del fluido un moto.
Per l'ipotesi di incomprimibilità del fluido osserviamo che il volume del fluido che in un certo tempo attraversa la sezione del condotto non varia con la sezione, altrimenti si avrebbe accumulo o rarefazione di fluido in alcune regioni nelle quali la densità aumenterebbe o diminuirebbe in contraddizione con l'ipotesi di incomprimibilità.
Equazione di continuità
Supponiamo di avere un condotto di sezione variabile. Per ipotesi il fluido sia incomprimibile (viscoso o meno): ad un certo volume di fluido entrante nel tubo corrisponderà un ugual volume di fluido uscente .
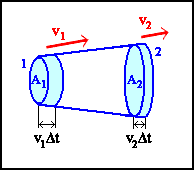
Fig.9: condotto di sezione variabile
Se all'entrata, nel punto 1, la velocità del fluido è v e la sezione del condotto è A1, nell'intervallo di tempo D t sarà passato un volume di fluido D V1 = A1 v1 D t
Nel punto 2 la velocità del fluido non sarà necessariamente la stessa del punto 1 : sarà una certa velocità v2 corrispondente ad una sezione A2 del tubo. Nello stesso intervallo D t di tempo uscirà quindi dal punto 2 un volume di fluido D V2 = A2 v2 D t
Per l'incomprimibilità del fluido questi volumi saranno uguali e quindi :
A1v1D
t=A2v2D
t (6)
A1v1=A2v2 (7)
Questa equazione è detta equazione di continuità.
La grandezza Av è detta portata in volume Qv e dall'equazione di continuità si deduce che in una corrente stazionaria di un fluido incompressibile la portata in volume ha lo stesso valore in ogni punto del fluido :
Qv = A v = costante (8)
Nel caso di fluidi viscosi, poichè la velocità varia sulla sezione del condotto, W sarà la velocità media e varrà:
Qv / A= cost (9)
Equazioni integrali per il moto dei fluidi
Sono equazioni che esprimono i bilanci macroscopici, utili per la soluzioni di molti problemi di ingegneria; è possibile ottenerle indifferentemente sia dall'applicazione delle leggi fondamentali della meccanica e della termodinamica, secondo lo schema di Eulero, ad un sistema aperto di estensione finita, sia dall'integrazione lungo il tubo di flusso delle equazioni differenziali per il moto isotermo.
Qualunque sia il procedimento prescelto, la deduzione delle equazioni integrali richiede come ipotesi di base di assegnare alle proprietà fisiche e alla velocità un valore uniforme su ogni sezione aperta al flusso di materia, ipotesi che del resto viene utilizzata in termodinamica per lo studio dei sistemi aperti.
Per quanto si riferisce alla proprietà termodinamiche, l'errore introdotto è del tutto trascurabile, specie se le sezioni di passaggio sono localizzate con un minimo di accortezza.
Per quanto si riferisce invece alla velocità, è necessario innanzitutto definirne il valore medio secondo la relazione:
W = (ò S u× n dS )/S (10)
essa pertanto è quella velocità che se fosse uniformemente distribuita su tutta la sezione darebbe la stessa portata in volume che si ha con la reale distribuzione della velocità.
L'introduzione del valor medio della velocità per la valutazione dell'energia cinetica comporta un errore di entità rilevante nel caso del moto laminare (100% in condotti a sezione circolare) ma modesta nel caso, tecnicamente più frequente, di moto turbolento.
Delimitiamo un tronco di tubo di flusso con due sezioni (S) trasversali 1 e 2; dall'equazione di continuità otteniamo:
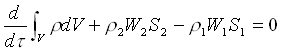 (11)
(11)
essendo, per definizione, nullo il flusso del vettore velocità attraverso la superficie laterale.
Definite le portate in volume e in massa, rispettivamente:
Qv = W S(12)
Qm = W S r (13)
dalla (11) si ha che:
si consideri in seno a un fluido in moto in regime stazionario un tubo di flusso delimitato da due sezioni trasversali 1 e 2.
Nell'ipotesi che il fluido sia sottoposto al solo campo di gravità (gz essendo z la quota del baricentro della sezione) e che sia possibile sostituire alla componente della velocità nella direzione s della linea di corrente (coincidente con l'asse nel caso in cui il tubo di flusso occupi l'intero condotto entro cui scorre il fluido) la velocità media w, la componente dell'equazione del moto lungo la s vale:
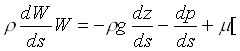 Ñ
2u+1/3 grad div u]s (14)
Ñ
2u+1/3 grad div u]s (14)
moltiplicando per ds e integrando la stessa fra le sezioni 1 e 2, si ottiene:
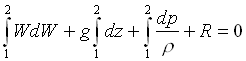 (15)
(15)
dove il termine R sta ad indicare il prodotto tra la forza frenante, operante su 1 Kg di fluido e dovuta alla viscosità, per lo spostamento della stessa e quindi il lavoro specifico fatto dal fluido contro la forza d'attrito dovuta alla viscosità, o anche l'energia meccanica specifica resa inutilizzabile per effetto della irreversibilità dei fenomeni d'attrito.
Essendo il volume specifico v uguale al reciproco della densità r , dalla (15) si ha infine:
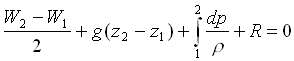 (16)
(16)
e per un fluido a densità costante:
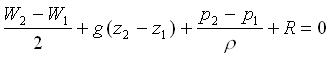 (17)
(17)
Per un fluido perfetto, essendo m = 0, si deduce l'equazione di Bernoulli:
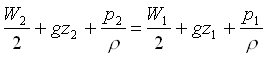
![]() (18)
(18)
valida per i fluidi incomprimibili.
La (16) rappresenta in particolare il bilancio dell'energia meccanica per un sistema aperto, meccanicamente isolato con l'esterno: qualora il sistema scambi energia meccanica con l'esterno, il corrispondente termine rappresentante il lavoro specifico l(inteso come positivo se fatto dal sistema verso l'esterno) influisce nello stesso senso di R (lavoro fatto dal sistema contro le forze di attrito) e pertanto deve essere aggiunto al primo membro. Qualora si abbia un condotto all'interno del quale fluisce un fluido in regime stazionario e nel quale è inserita una macchina motrice od operatrice, il bilancio dell'energia meccanica del sistema si esprime quindi con l'equazione:
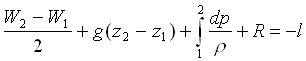 (19)
(19)
come già si è visto non esiste, in assoluto, un fluido incomprimibile. D'altro canto, in base a quanto sopra esposto, appare evidente l'utilità di poter considerare, nella soluzione di certe categorie di problemi, l'equazione di stato nella forma r = cost.
Per ottenere un criterio di massima che ci permetta di individuare i limiti entro cui è tecnicamente possibile utilizzare la schematizzazione del fluido incomprimibile, e gli errori che da essa discendono, è necessario eseguire un ragionamento per ordine di grandezza.
Dalla (15) se consideriamo la sezione A del tubo costante ( cioè W1 = W2 ) e trascuriamo i contributi derivanti dall'attrito e dalla gravità ( cioè z1 = z2 ), considerando il termine R trascurabile, si ottiene:
D p ~ -l r . (20)
Parabola di Poiseuille
Consideriamo un fluido che imbocca un condotto provenendo da un grande serbatoio: il profilo di velocità, inizialmente piatto, o quasi, si deforma via via fino ad assumere la configurazione detta PARABOLA DI POISEUILLE, che vedremo dopo in forma analitica. Nella fig.10 , sono evidenziati alcuni profili di velocità in regione d’ingresso. Al rallentamento del fluido all’interno dello strato limite, corrisponde un’accelerazione di quello che si trova fuori, dovendo essere garantita la continuità di portata. Se la lunghezza del condotto è sufficiente in relazione al suo diametro, i confini dello strato limite tendono ad incontrarsi sull’asse del condotto: in teoria il contatto si ha solo asintoticamente, ma in pratica a circa 20-30 diametri dall’imbocco si può ritenere che il profilo abbia ormai raggiunto la sua configurazione definitiva, che viene detta PROFILO COMPLETAMENTE SVILUPPATO, sia esso laminare o turbolento.
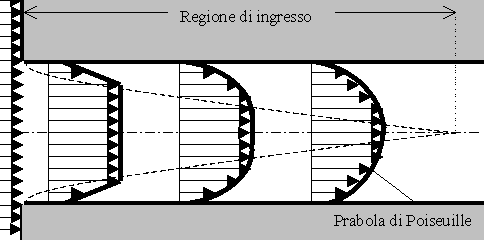
Fig.10: sviluppo dello strato limite dinamico nella regione d’ingresso
Prendiamo dunque un tubo liscio a sezione circolare con raggio R, in cui scorre del liquido con velocità u e consideriamo un elemento di volume di lunghezza L e raggio r, centrato rispetto al piano di simmetria del condotto (Fig.11).
Poniamo le seguenti ipotesi:
· Sistemo stabilizzato
· Moto laminare
· Regime stazionario rispetto a spazio e tempo
· Fluido viscoso Newtoniano e incomprimibile
· Forza peso trascurabile
Voglio determinare la perdita di pressione ( o di carico) del fluido dovuta a fenomeni di tipo viscoso. Tale perdita di pressione è infatti causata dalle tensioni tangenziali che frenano il fluido in movimento, oppure, equivalentemente, se mi pongo in un punto di vista solidale con il fluido, è dovuta alle tensioni tangenziali scaricate dal fluido stesso sulle pareti del condotto in modo da trascinarlo nel suo moto.
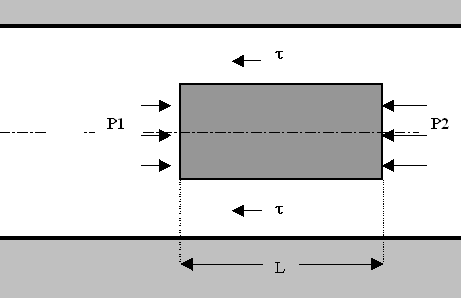
Fig.11:bilancio delle forze agenti su un elemento di volume di fluido in moto
Il bilancio delle forze, che deve essere nullo, si compone di 3 contributi: la pressione p![]() che agisce sulla faccia d’entrata, la contropressione p
che agisce sulla faccia d’entrata, la contropressione p![]() sulla faccia d’uscita e la forza tangenziale t
che frena il fluido in movimento.
sulla faccia d’uscita e la forza tangenziale t
che frena il fluido in movimento.
Considerando positiva la direzione che va da sinistra verso destra, abbiamo che il contributo di p![]() è positivo, mentre i contributi di p
è positivo, mentre i contributi di p![]() e t
sono negativi in quanto vanno in direzione opposta a p
e t
sono negativi in quanto vanno in direzione opposta a p![]() .
.
L’equazione di bilancio delle forze diventa quindi:
![]() (21)
(21)
dove 2p
RL è l’area laterale del tubo cilindrico e p
R![]() è l’area della sezione del tubo.
è l’area della sezione del tubo.
Se considero un cilindretto di raggio r < R, la (21) diventa:
![]() (22)
(22)
Sostituisco ora nella (22) la legge di Newton 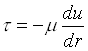 ed ottengo:
ed ottengo:
(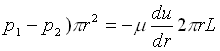 (23)
(23)
ovvero, facendo le opportune semplificazioni, abbiamo
![]() (24)
(24)
Integriamo ora questa equazione differenziale a variabili separabili considerando l’ipotesi di aderenza:
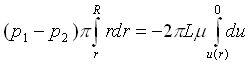 (25)
(25)
cioè, svolgendo i calcoli:
(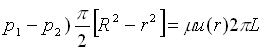 (26)
(26)
Possiamo ora ottenere la PARABOLA DI POISEUILLE, cioè la legge che mi descrive come varia la velocità u rispetto al raggio r:
u(r)=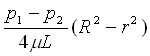 (27)
(27)
Possiamo adesso calcolare la velocità media w (secondo la definizione) :
w =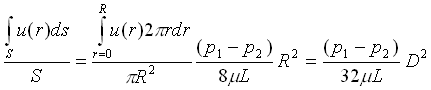 . (28)
. (28)
Tabella 1: viscosità dinamica m dei principali liquidi e gas
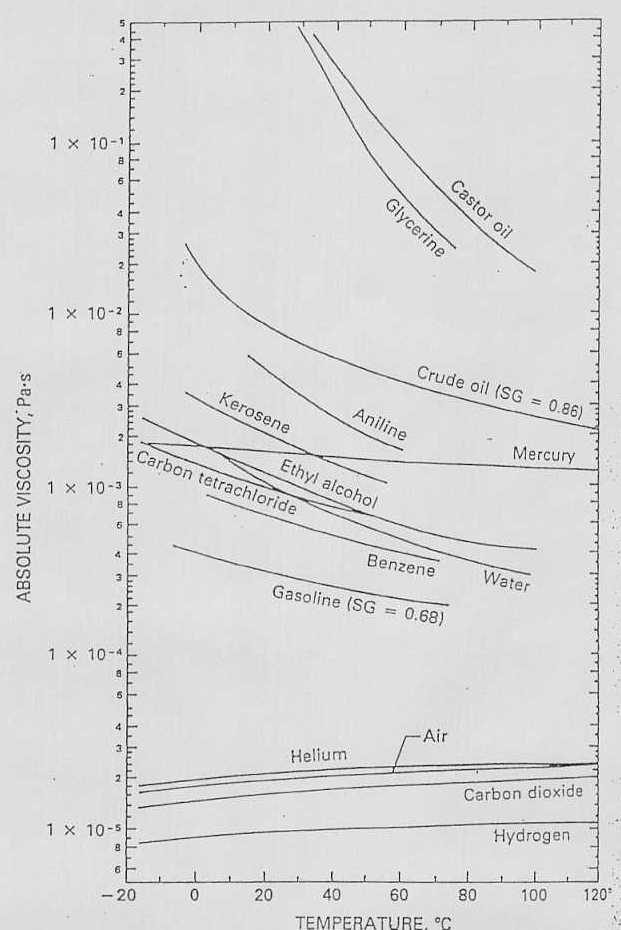
Tabella 2: viscosità cinematica n dei principali liquidi e gas