Filippo Magrini mat.132081 Lezione del 27/11/2000 ore 16.30-18.30
Tecniche avanzate di misura della
risposta all’impulso
Universitá
degli Studi di Parma
Corso
di Fisica Tecnica
Nella analisi di un campo acustico possiamo ragionevolmente ipotizzare che il nostro sistema, considerato da quando il segnale è generato dall’uscita della scheda audio del computer a quando, tramite un microfono, rientra nella scheda stessa, sia un sistema lineare tempo invariante.
h
x(t) y(t)
![]()
![]()
ingresso uscita
Il sistema è stato schematizzato con il concetto di black box.
h è la risposta all’impulso del sistema.
x e y sono rispettivamente il segnale di ingresso e uscita.
Ricordiamo che un sistema si dice lineare se l’uscita é una funzione lineare dell’entrata, ovvero se vale il principio di sovrapponibilitá degli effetti . Il principio di sovrapponibilitá degli effetti si può esprimere così: dati due ingressi generici A e B e le loro relative uscite C e D, ottenute applicando singolarmente gli ingressi, applicando nel sistema l’ingresso A+B si ottiene l’uscita C+D.
Secondo questa ipotesi la risposta all’impulso è univocamente determinata dal legame matematico che lega l’ingresso con l’uscita di un sistema lineare tempo invariante.
Questo legame matematico è rappresentato dal cosiddetto teorema della convoluzione.
![]() ( 1 )
( 1 )
Quando passiamo da un sistema continuo con segnali analogici a un sistema discreto con segnali campionati, come accade in un computer, l’integrale diventa una sommatoria.
Abbiamo quindi che il tempo corrente è i volte l’intervallo di campionamento Δ τ .
( 2 )
![]()
L’intervallo di campionamento è quello imposto dalla scheda audio.
Il segnale campionato in uscita risulta:
![]()
( 3 )
Dove N è il numero di campioni che rappresenta la risposta all’impulso.
Passiamo ora dal dominio del tempo al dominio della frequenza eseguendo la Fast Fourier Transform (FFT):
![]()
![]() x FFT
X(ω)
x FFT
X(ω)
![]()
![]() y FFT
Y(ω)
y FFT
Y(ω)
![]()
![]() h FFT
H(ω)
h FFT
H(ω)
X(ω) e Y(ω) sono gli spettri rispettivamente del segnale d’ingresso e del segnale di uscita.
H(ω) è la funzione di trasferimento di un sistema lineare tempo invariante.
Possiamo ora riscrivere il teorema della convoluzione nel dominio della frequenza.
![]() ( 4 )
( 4 )
L’operatore convoluzione nel dominio delle frequenze si traduce in una banale moltiplicazione.
In generale la convoluzione nel tempo può essere espressa in questo modo:
y(τ) = IFFT [ FFT (x) · FFT (y) ] ( 5 )
Dove IFFT è la trasformata di Fourier inversa (Inverse Fast Fourier Transform).
Conoscendo x (segnale che genero) e y (segnale che misuro) voglio ottenere h.
Nel dominio della frequenza:
![]()
( 6 )
Nel dominio del tempo :
![]()
( 7 )
Quanto enunciato finora costituisce la base metodologica per la misura della risposta all’impulso con la tecnica elettroacustica. Questi principi funzionano con ogni tipo di segnale, purchè esso abbia uno spettro che copra tutte le frequenze (rumore bianco, rumore rosa, una sinusoide sweepata, o anche musica o parlato).
Tuttavia, tanto più i segnali hanno poca variabilità nell’utilizzo delle varie frequenze, tanto più lungo deve essere il campione da analizzare. Questo è il caso, in particolare, di musica e parlato.
L’utilizzo di segnali quali il rumore bianco, che ha la stessa energia ad ogni frequenza, mi consente di minimizzare i tempi di misura.
In ogni caso esiste, comunque, un tempo di misura minimo. Infatti, per ricostruire correttamente la risposta all’impulso di un sistema, devo utilizzare segnali la cui rappresentazione in frequenza sia la trasformata di un numero di punti maggiori di N. Siccome nel fare la FFT la trasformazione deve essere fatta con un multiplo di 2, se io ho una risposta all’impulso di un certo numero di punti (ad esempio 96000), ho bisogno del primo multiplo di 2 successivo ( 131072 ).
Inoltre devo fare la misura di un tempo minimo che è costituito da un periodo del segnale più lungo della risposta all’impulso. Se così non faccio mi espongo al fenomeno del time aliasing, a causa del quale la coda del segnale non misurata mi si sovrappone alla parte iniziale.
Gli analizzatori FFT, tuttavia, sono in grado di fare una trasformata FFT al massimo dell’ordine di poche migliaia di punti (negli strumenti più potenti Nmax dell’ordine di 4096 punti). Sono quindi inutilizzabili, per quanto precedentemente detto, per la misura acustica di una sala. Fino a qualche tempo fa questo era un ostacolo insormontabile, in quanto la potenza di calcolo necessaria a fare un’ FFT con N = 131072 richiedeva giorni di calcolo.
Tecnica MLS (Maximum Length Sequence)
Per ovviare a questo problema il matematico tedesco Alrutz inventò la tecnica MLS .
Essa consiste nell’utilizzo di un segnale binario generato con un operatore logico chiamato shift register (registro di scorrimento).A ogni passo di campionamento ogni cella (che contiene uno 0 o un 1) comunica il proprio valore alla cella alla sua destra, il valore dell’ultima cella esce, e l’ingresso viene rialimentato con un operatore logico XOR, posto fra un’opportuna cella intermedia e l’uscita.
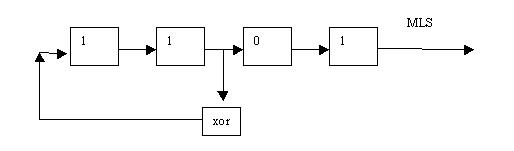
Fig.1 - Shift register a 4 bit
Fig. 1 - Shift register a 4 bit, i numeri scorrono a destra ad ogni passo.
Il segnale di uscita assomiglia ad un’onda quadra in cui varia la lunghezza del tratto “su” e del tratto “giù”, e all’ascolto sembra il rumore bianco.
Un’importantissima proprietà del segnale MLS di massima lunghezza è che se lo si autocorrela si ottiene una δ di Dirac, quindi un impulso ideale.
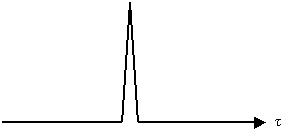
Fig. 2 – La funzione δ di Dirac
Questa proprietà ci consente di non utilizzare l’algoritmo della FFT, in quanto è sufficiente generare il segnale di tipo MLS x d’ingresso, campionare il segnale y di uscita e crosscorrelare x con y.
La crosscorrelazione nel tempo produce la risposta all’impulso h.
Infatti:
y = x Ä h , ( x Ä h ) crosscorrelato (x) = [ (x) crosscorrelato (x)] Ä h = h ( 8 )
L’esecuzione della crosscorrelazione viene eseguita ottimamente tramite la Fast Hadamard Transform (FHT), corrispettivo della FFT applicata a segnali binari.
Il grande vantaggio della FHT rispetto alla FFT è quello di richiedere tempi di calcolo molto inferiori.
Facendo la FHT del segnale y, cioè del risultato della misura, si ottiene h nel dominio del tempo senza passare dal dominio della frequenza.
Tramite questa tecnica si poteva misurare la risposta all’impulso di sistemi con un numero N di campioni grande.
Tipicamente, all’epoca (’87-’88) Nmax era 65536 (massimo dato di memoria che si potesse allocare come singolo vettore in un sistema a 16 bit). Considerando che un tempo di riverbero di 1,5 secondi corrisponde a circa 60000 punti campionati a 44100 Hz , se l’ambiente non è troppo riverberante la tecnica si rivela soddisfacente.
In caso contrario, se l’ambiente mi richiede di misurare tempi di riverbero più lunghi, posso ridurre la frequenza di campionamento. Con lo stesso sistema dell’esempio precedente, a 22 kHz, ho un tempo di misura di 3 secondi.
All’epoca la tecnica MLS veniva realizzata con uno shift register hardware, cioè la scheda Melissa.
Esperienza 1:
Andiamo ora a fare una misura sul segnale MLS usando un microfono Soundfield.

Fig. 3 – Microfono Soundfield con relativa interfaccia.
Si tratta di un microfono a 4 capsule, montate ai 4 vertici di un tetraedro, e 4 canali: uno (w) contiene il segnale di pressione, gli altri tre (x,y,z) contengono le 3 componenti cartesiane della velocità.
Il microfono per la pressione (w) è omnidirezionale, i tre per la velocità (x,y,z), orientati secondo gli assi cartesiani, sono a 8.

Fig.4 – microfono omnidirezionale (sinistra), e a 8 (destra)
Generiamo il segnale MLS a 16 bit (anche se sarebbe sufficiente 1 bit solo, essendo un segnale binario) a 48 kHz.
Ripetiamo il segnale 8 volte per migliorare il rapporto sgnale – rumore.
Fig. 5 - Segnale MLS ripetuto 8 volte.
Fig. 6 - Segnale di risposta registrato con il microfono.
Otteniamo così la risposta all’impulso.
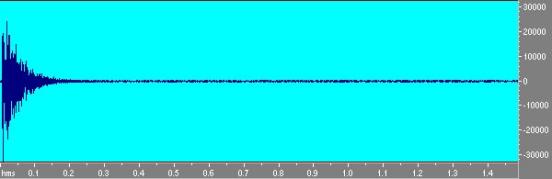
Fig. 6 - Risposta della stanza ottenuta con MLS.
Fig. 7 Risposta della stanza ottenuta con MLS
Per ogni canale è possibile vedere il suono diretto e ciascuna delle singole riflessioni.
Tecnica della sinusoide sweepata:
L’alternativa al segnale MLS è costituita dal segnale sinusoidale sweepato, quindi un segnale la cui frequenza varia progressivamente nel tempo.
Anziché utilizzare la trasformata di Hadamard (applicabile solamente a segnali binari), la sinusoide sweepata sfrutta la trasformata di Fourier. L’utilizzo di questa tecnica è stato reso possibile solo di recente grazie all’aumentodella potenza dei sistemi di calcolo avvenuta negli ultimi 2 anni.
In realtà la tecnica di misura del segnale sweepato veniva usata già 11 anni prima, in quanto era stata sviluppata una tecnica chiamata Time Delay Spectrometry (TDS), utilizzata anche per misure di tipo radio trasmittente.
Nella TDS si usa una sinusoide sweepata linearmente, quindi la frequenza varia da un valore f1 a un valore f2 in modo lineare nel tempo.
![]()
f

![]() f2
f2
![]() f1
f1
![]()
τ
Fig. 8 - sinusoide sweepata linearmente nel tempo (τ) da una frequenza f1 iniziale a una frequenza f2 finale
Dal punto di vista spettrale possiamo dire che lo spettro di una sinusoide sweepata linearmente è uno spettro bianco, infatti il segnale ha la stessa energia in ogni intervallo di numero di Hertz costante.
Tradizionalmente, la misura della sweepata si svolgeva facendo passare il segnale ripreso dal microfono attraverso un filtro inseguitore. Esso non era altro che un filtro passa-banda molto stretto (lascia passare una gamma di frequenze molto ristretta). Il filtro veniva fatto variare nel tempo, “spazzolando” tutto il campo delle frequenze ricoperto dalla sinusoide.
Se filtro e sinusoide sono sincronizzati rilevo l’onda diretta. Se invece faccio passare il filtro inseguitore con ritardi via via crescenti, rilevo il suono riverberato. È così possibile costruire una rappresentazione tempo-frequenza riconducibile ad una risposta all’impulso.
Recentemente si è però passati a una soluzione molto più agevole per trovare la risposta all’impulso h.
Essa consiste nella convoluzione del segnale di uscita y con un opportuno filtro inverso x’ tale che:
y Ä x’ = x Ä h Ä x’ = h ( 8 )
Questo è vero se : x Ä x’ = 1 (δ di Dirac)
Ovviamente, il segnale x’ che ci occorre è la sweepata stessa x rovesciata sull’asse dei tempi.
![]()
f


![]() f2
f2
x
x’
![]() f1
f1
![]()
τ
Fig. 9 – Andamento del segnale x e del filtro inverso x’ nel dominio del tempo
Difetto della sinusoide sweepata linearmente è quello di avere molta energia alle alte frequenze rispetto alle basse.
Il nostro obiettivo, al contrario, è quello di avere più informazioni alle basse frequenze, dove, normalmente si hanno i maggiori problemi.
Per avere più risoluzione alle basse frequenze utilizziamo una sinusoide sweepata in modo lineare rispetto ad una scala dei tempi logaritmica, ovvero in cui la frequenza varia in modo esponenziale rispetto a una scala dei tempi lineare. In questo caso l’energia del segnale di ingresso x cala di 3 db/ottava.
Svantaggio di questa soluzione è che per deconvolvere la risposta all’impulso non è più possibile usare, come filtro inverso, l’immagine speculare dell’ingresso x rovesciata sull’asse dei tempi. Questo è dovuto al fatto che, calando sia il segnale y = x Ä h che il segnale x’ di 3 db/ottava, la loro convoluzione mi dà una risposta all’impulso che è filtrata con un filtro passa-basso di 6 db/ottava, quindi assolutamente inattendibile.
La soluzione corretta consiste nel convolvere il segnale misurato y, con un filtro inverso x’, costituito dal segnale x rovesciato sull’asse dei tempi, pre-equalizzato in modo da crescere di 6 db/ottava, per compensare la caduta della risposta all’impulso.
Esperienza 2:
Generiamo per tre volte una sinusoide alla frequenza di campionamento di 48 kHz, mono, a 32 bit, sweepata in modo esponenziale, da 50 Hz a 20 kHz.
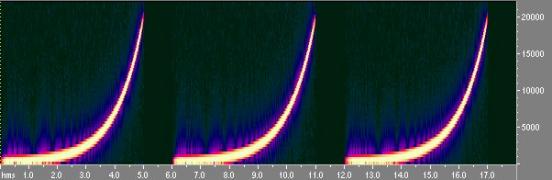
Fig 6 Sequenza di tre sweep vista con Cool Edit spectral view
Fig. 10 - Sequenza di tre sweep esponenziali vista con Cool Edit
Misuriamo il segnale di uscita con un microfono.
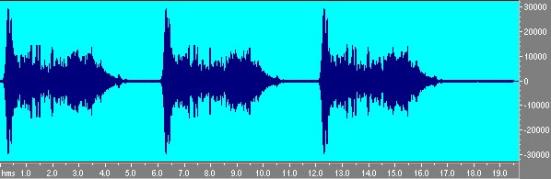
Fig. 11 - Misura alla sequenza di tre sweep.
Ora bisogna convolvere con lo sweep inverso, che il plug-in di generazione dello sweep ha già posto nella clipboard.
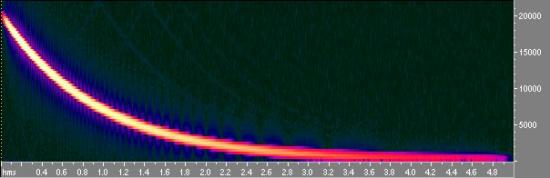
Fig. 12 - Sweep inverso visto con Cool Edit
Otteniamo così la risposta all’impulso della stanza.
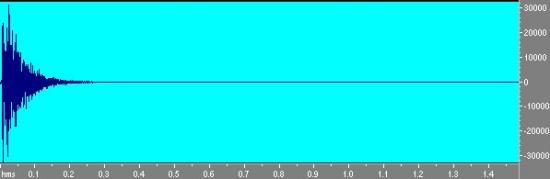
Fig. 13 - Risposta della stanza ottenuta da sweep e mediata.