MOTO ESTERNO
Una parte importante della fluidodinamica è rappresentata dallo studio del moto esterno.
COS’È IL MOTO ESTERNO?
Dopo aver analizzato il moto di un fluido all’interno di un corpo cavo (un tubo, un condotto, ecc.) studieremo il comportamento del moto di un fluido attorno ad un corpo, detto comunemente moto esterno. Studieremo nella stessa maniera il caso in cui sia un oggetto in movimento ad attraversare un fluido fermo rispetto a quello in cui sia il liquido a muoversi intorno ad un corpo fermo. Sappiamo infatti che ognuno dei due casi può essere ricondotto all’altro semplicemente cambiando le condizioni del moto dell’osservatore.
Nell’ambito industriale lo studio del moto esterno è generalmente circoscritto all’utilizzo dell’aria come fluido; in tal caso si parla correntemente di aerodinamica.
Per studiare il moto esterno inizieremo con l’analisi bidimensionale di alcuni corpi elementari e simmetrici che si prestano ad alcune semplificazioni: la lastrina piana, il cilindro e la sfera.
LASTRINA PIANA
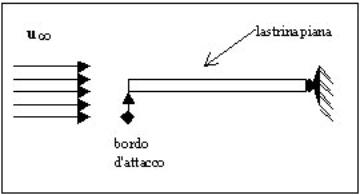
Fig.1-Lastrina piana investita da un flusso.
Prendiamo una lastrina piana di lunghezza infinita e spessore trascurabile investita da un fluido avente velocità u∞ che scorre longitudinalmente alla superficie della lastrina stessa(fig2). In prossimità del corpo il moto del fluido subirà una variazione; si intuisce però che ci sarà una certa distanza dalla lastrina dopo la quale il moto del fluido non subirà più la perturbazione dovuta al corpo. Chiameremo strato limite la superficie sulla quale il liquido ha una velocità
u*![]() (1)
(1)
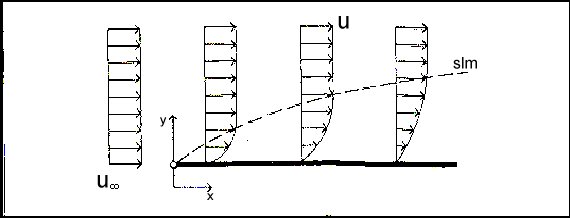
Fig2 Strato limite – lastrina piana
Definiremo quindi lo spessore dello strato limite come la distanza tra il corpo e la superficie dello strato limite. Abbiamo così potuto restringere l’analisi del comportamento del fluido alla sola regione interna allo strato limite, sapendo che all’esterno esso scorre praticamente imperturbato. Data la simmetria del corpo preso in analisi ci limiteremo a studiare l’andamento del fluido tra la superficie superiore della lastrina e lo strato limite. I risultati ricavati saranno validi anche per la parte inferiore. Rifacendoci allo studio del moto interno possiamo ancora ritenere valida l’ipotesi per cui le particelle di liquido strettamente a contatto con il corpo non sono in moto rispetto allo stesso (ipotesi di aderenza). Partendo da questo presupposto e osservando la figura2 notiamo che la velocità del liquido dovrà aumentare da 0 a uslm sull’asse delle ordinate. Ciò comporta la presenza di una forza trasversale che può essere quantificata, secondo la legge di Newton, in
con u velocità del fluido, υ viscosità del fluido e n normale rispetto alla superficie della lastra.
La presenza di una tensione tangenziale porterà all’esistenza di una forza tangenziale quantificabile in
![]() =
= ![]() (3)
con S superficie su agisce la forza
(3)
con S superficie su agisce la forza
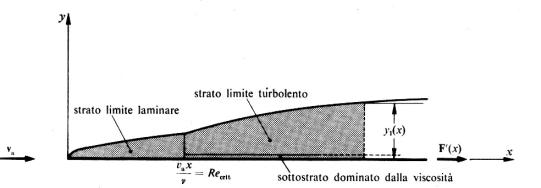
fig3 strato limite laminare e turbolento – lastrina piana
L’ipotesi di viscosità del fluido comporta la non omogeneità del moto del fluido all’interno dello strato limite. Conoscendo il funzionamento del moto interno possiamo plausibilmente ipotizzare che tale moto assumerà due differenti tipologie: laminare e turbolento. Fissando il bordo d’attacco (vedi fig3) come riferimento per le ascisse, possiamo considerare che fino ad un dato punto xcr il moto sarà di tipo laminare; da xcr in avanti sarà turbolento se non in una piccola area adiacente al lamierino in cui manterrà una caratteristica laminare.
Definendo il numero di Reynolds in funzione di x
![]() (4)
(4)
e ponendo Rex del punto critico
troveremo la coordinata xcr come
![]() (5)
(5)
CILINDRO (SFERA E FIGURE AFFINI
)
fig 4 cilindro investito da un fluido
Il caso appena analizzato è però quasi privo di applicazioni pratiche, in quanto anche l’unico caso che vi si può ricondurre, l’aereo ad ala piatta, comporta l’ipotesi di avere un angolo d’attacco non nullo rendendo quindi non trascurabile la componente normale della forza (dipendente dalle variazioni di pressione del fluido).
Ben più interessanti dal punto di vista tecnico sono invece il cilindro (fili alta tensione, camini, ecc.) e la sfera (goccia d’acqua, pallone, ecc.).
Per prima cosa analizzeremo un cilindro investito radialmente da un fluido incomprimibile ideale. Anche in questo caso il corpo costituisce un ostacolo per il fluido il cui moto subisce localmente una perturbazione. Prendendo come riferimento il punto A in figura5 (θ=0°) posso analizzare le iterazioni corpo-fluido al variare dell’angolo θ.
Ipotizzando come nel caso precedente l’esistenza di una zona al di fuori della quale il moto del fluido è indisturbato, possiamo restringere i nostri studi ad un’area limitata.
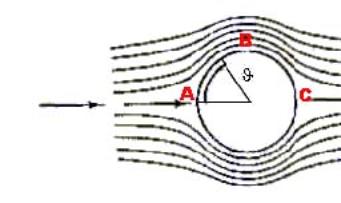
fig 5 cilndro investito da un fluido, vista laterale
Nel punto A, analogamente a ciò che accade nel tubo di Pitot, si ha un fenomeno di ristagno del fluido e sia ha quindi la pressione massima (del fluido sul corpo) pr (pressione di ristagno).
Nel punto B la sezione attraversabile dal fluido è diminuita sensibilmente quindi, data l’incomprimibilità del fluido stesso, sappiamo che esso ha acquistato velocità. Per l’effetto Venturi a ciò è associata una diminuzione della pressione, che raggiunge il suo valore minimo in θ=90° (analogamente in θ=270°) per poi aumentare e raggiungere nuovamente il valore pr nel punto C (θ=180°).
In tal modo le forze agenti sul corpo sono perfettamente bilanciate e ciò vale anche per la sfera ed il cilindro allungato.
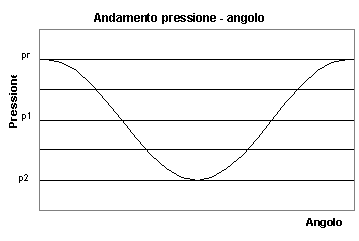
fig6 andamento della pressione sulla superficie del cilindro – caso ideale
Con l’ipotesi di fluido ideale e quindi di viscosità nulla abbiamo cioè visto che gli sforzi normali sono bilanciati e quelli tangenziali sono nulli per definizione, quindi lo stato del corpo non subisce alcun tipo di modificazione. Ciò in realtà non accade e si verifica il paradosso di D’Alambert secondo cui non esistono fluidi ideali.
Nel caso reale, quindi esisterà una forza di trascinamento Ft dovuta alla presenza (trascurata in precedenza) di forze tangenziali ed alle perdite di carico (la pressione in C sarà minore rispetto che in A, quindi le forze normali non saranno + bilanciate).
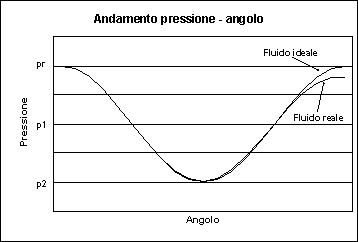
fig7 andamento della pressione sulla superficie del cilindro – confronto caso ideale - reale
Tutto ciò è dimostrabile analiticamente applicando l’equazione di Bernoulli
![]()
![]() (6)
(6)
TEORIA DEI MODELLI
In realtà quasi in nessuna caso che si presenta nelle applicazioni industriali potremo calcolare l’andamento delle della forza di trascinamento analiticamente come abbiamo cercato di fare per i solidi elementari.
In corpi geometricamente complessi (pensiamo ad un’automobile) sarà quasi impossibile trovare le equazioni che regolano l’andamento di pressione e forza tangenziale nei vari punti della superficie dell’oggetto in questione.
Dovremo quindi cercare i dati che ci interessano sperimentalmente, ad esempio tramite l’uso di una galleria del vento (vedi approfondimento) se come fluido utilizziamo l’aria.

fig8 B. Engineering Edonis nella galleria del vento pininfarina
Ma se questa è una strada percorribile per oggetti di dimensioni medio – piccole, ciò non è fattibile per corpi di grandi dimensioni come un aereo o un palazzo.
Ricorreremo quindi ad un escamotage.
La teoria dei modelli di Reynolds ci viene incontro enunciando che per studiare un sistema con lunghezza caratteristica L è possibile usare un modello in scala di lunghezza caratteristica L’<<L. Per ricavare il comportamento del sistema originale riporteremo su di esso i dati del modello opportunamente corretti tramite l’uso di numeri puri.
Ora dobbiamo trovare le grandezze che ci permetteranno questa “conversione”.
La prima è l’area frontale. Cosa si intende per area frontale? L’area frontale (vedi fig) è la proiezione dell’oggetto su un piano perpendicolare alla direzione del vettore velocità del fluido
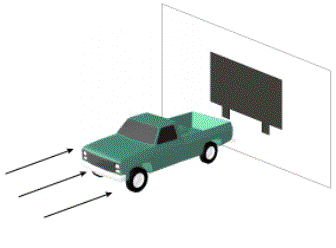
fig9 area frontale di un pick-up
Ma per calcolare numericamente la forza di trascinamento possiamo rifarci alla teoria dei modelli di Reynolds, che ci permette di ridurre il calcolo di Ft a pochi parametri, e di avere un’equazione risolutiva indipendente dalla forma del corpo. In pratica conoscendo alcuni valori caratteristici del corpo e del fluido non abbiamo bisogno di studiare la geometria e l’andamento dei flussi sul corpo stesso (e ci verrà molto utile nei corpi asimmetrici) ma possiamo calcolare direttamente Ft. Naturalmente si tratterà di utilizzare valori sperimentali e ricavati da grafici (vedi figg 12-13), quindi ci saranno vari fattori ad influenzare la precisione del calcolo stesso.
CORPI ASIMMETRICI - PROFILO
ALARE
Quando lo studio del moto esterno si sposta su corpi asimmetrici, si vede innanzitutto che non si può più dare per scontato il bilanciamento delle forze normali; per questo motivo la Forza di trascinamento non sarà più longitudinale al profilo di velocità del fluido. Per facilità di calcolo divideremo allora la Forza di trascinamento in due componenti ortogonali: la Forza di resistenza (longitudinale alla velocità) e la Forza di portanza (perpendicolare alla velocità).
Il caso più interessante è sicuramente quello dell’ala di aereo (il fluido è ovviamente l’aria).
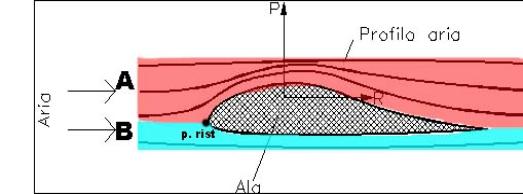
fig10 flussi d’aria intorno ad un’ala
Vediamo subito che il punto di ristagno non è più in posizione centrale e che l’aria, a seconda che passi al di sopra o al di sotto di tale punto compie un tragitto di lunghezza differente. Consideriamo come per il cilindro di restringere la nostra analisi ad una zona delimitata in cui si può racchiudere la perturbazione del moto del fluido; definiamo flusso A la parte di aria che passa al di sopra del punto di ristagno e flusso B quella che ne passa al di sotto. Osserviamo che il flusso A deve attraversare un’area proporzionalmente minore a quella attraversata dal flusso B; ne consegue che il flusso A avrà una velocità maggiore rispetto al flusso B. Per l’effetto venturi sappiamo che il fluido a velocità maggiore avrà una pressione minore (fig10), per cui le forze normali esercitate sulle superfici dell’ala non saranno bilanciate, ma sarà maggiore quella esercitata sulla superficie inferiore. Da questo nasce una certa forza indirizzata verso l’alto che è quella che abbiamo indicato inizialmente come forza di portanza. La componente di forza di resistenza sarà data analogamente ai casi precedenti dalle forze tangenziali esercitate dall’aria sulle superfici dell’ala.
Nella progettazione delle ali assume quindi una certa importanza il rapporto Fp/FR; poiché la FR dovrà bilanciare la forza peso dell’aereo, maggiore sarà questo rapporto, minore sarà la forza da applicare (Fp) per far volare l’aereo stesso. Solitamente si arriva ad avere dei rapporti di 4-5:1.
Per calcolare numericamente Fp e FR utilizzeremo il sistema utilizzato in precedenza, cioè ci rifaremo alla teoria dei modelli di Reynolds. Definiamo
F![]() _ forza di trascinamento
_ forza di trascinamento
![]() _ densità del fluido
_ densità del fluido
Sapendo che Ft è la somma vettoriale delle due forze sopraccitate. In questo caso la lunghezza caratteristica che ci servirà per ricavare i coefficienti Cx e Cy sarà la corda alare, ovvero la distanza tra il bordo d’attacco e il bordo di uscita dell’ala (vedi fig). Inoltre, analizzando le forze agenti sull’aereo, come area frontale non dovremo prendere in considerazione quella che si incontra longitudinalmente al flusso, ma dovremo considerare quella vista guardando l’aereo dall’alto. Ciò è dovuto al fatto che la portanza è predominante rispetto alla forza di resistenza.
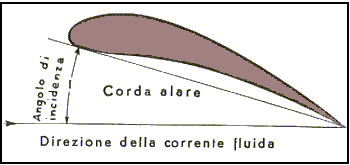
fig11 corda alare
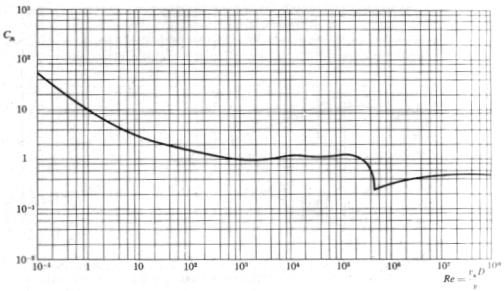
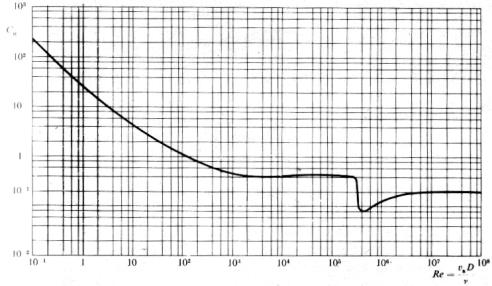
I valori di Cx sono solitamente messi in grafico con i rispettivi Re a seconda della forma analizzata. Possiamo vedere ad esempio:
ESERCIZI
ESERCIZIO 1

Fig14 B. Engineering Edonis (forse è difficile trovarla in prima corsia ai 120km/h!)
Un’automobile di area frontale Af=1,8 m² avente un coefficiente di attrito aerodinamico Cx=0,34 (con Cx = Cf) viaggia in autostrada in prima corsia ad una velocità u=120 Km/h. Calcolare la potenza erogata dal motore trascurando le perdite in attrito degli organi di trasmissione.
SOLUZIONE
Trascuriamo inizialmente l’attrito di rotolamento ed analizziamo solamente la forza FR che si oppone al moto dell’automobile.
Sapendo che il fluido è l’aria e considerando delle condizioni standard di temperatura (temperatura ambiente), ricaviamo da tabella i valori di viscosità e densità di massa:
![]()
![]()
Possiamo quindi calcolare FR come:
![]()
Sapendo che il lavoro è una forza per uno spostamento e che la potenza è un lavoro nel tempo, fissando un tempo fittizio t=1s posso calcolare la potenza come
Sapendo che 1cv equivale a 735W ottengo
La potenza erogata sembra molto piccola, ma in realtà a 120 Km/h l’attrito di rotolamento è ancora predominante rispetto a quello aerodinamico. Supponendo in prima approssimazione di avere un attrito di rotolamento
Frot![]() 25cv
25cv
ottengo che la potenza erogata dal motore è
![]() cv
cv
Provo ora a calcolare la potenza erogata nel caso in cui la macchina in questione si porti in terza corsia ad una velocità u=180Km/h.
La resistenza aerodinamica diventa
![]()
![]() cv
cv
e stavolta è predominate rispetto a quella dovuta all’attrito di rotolamento che in prima approssimazione possiamo considerare invariata.
La potenza erogata si attesta quindi su un valore di
![]() cv
cv
Ciò è dovuto al fatto che, mentre la resistenza aerodinamica varia col quadrato della velocità, l’attrito di rotolamento si può considerare slegato dalla velocità stessa alle basse velocità (intese come velocità minori di 500 Km/h, cioè basse in generale, non nell’ambito automobilistico!).
Abbiamo quindi visto come, per il raggiungimento di un’elevata velocità di punta, sia importante lavorare sull’area frontale e sul Cx della vettura, forse più ancora che sulla potenza del motore.
ESERCIZIO 2
Trovare la velocità di caduta di una goccia di pioggia sferica di diametro d=5mm
fig15 goccia d’acqua in caduta libera
SOLUZIONE
La goccia di pioggia, partendo da ferma, accelererà sotto la spinta della forza peso Fp fino a raggiungere una velocità in cui la forza di trascinamento Ft diventerà uguale a Fp. In quel momento, essendo le due forze bilanciate, la goccia avanzerà di moto rettilineo uniforme ad una velocità u che dobbiamo trovare.
Procederemo quindi uguagliando Fp a Fr.
![]()
quindi il suo peso
![]()
ma sapendo che
![]()
ponendo Fp = Fr ottengo
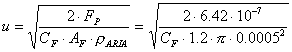
dove l’area frontale Af della sfera è il cerchio di diametro d
Abbiamo però ancora due incognite, u e Cf.
Per ricavare Cf possiamo rifarci al grafico Cf/Re ma, dato
Re![]()
vediamo che le due grandezze non possono essere ricavate separatamente tra loro. L’unico modo per risolvere il problema è quindi partire da una velocità ipotetica (è importante per arrivare velocemente alla soluzione corretta del problema scegliere una velocità plausibile) u 1
![]()
da cui ricavare Re
![]()
per poi calcolare
![]()
se u2 è abbastanza simile a u1, allora possiamo considerare il problema risolto. Altrimenti rifacciamo lo stesso procedimento, partendo però stavolta da u2 appena ricavata;
calcoliamo nuovamente Re, Cf e u
![]()
vedremo che la differenza tra le due velocità sarà diminuita e ripeteremo questa operazione finché non avremo ridotto la differenza ad un valore percentualmente accettabile per il grado di accuratezza richiesto ai nostri calcoli.
Nel nostro caso ci accontentiamo del risultato trovato e ci fermiamo
L’unico rischio di questo tipo di calcolo è quello di sbagliare ampiamente la prima ipotesi di velocità; in certi casi ciò può portarci a trovare dei valori di Re dalla parte “sbagliata” del ginocchio del grafico. Questo potrebbe farci arrivare ad avere come risultato un valore di velocità che non corrisponde al vero.
Proviamo ad esempio ad ipotizzare una velocità molto alta troviamo
![]()
a cui corrisponde
C![]()
In questo caso abbiamo preso una velocità molto grande, ma date le piccole dimensioni della goccia Re ha assunto un valore abbastanza piccolo che è rimasto a sinistra del ginocchio e ci permetterebbe lo stesso di arrivare alla soluzione corretta.
Se si fosse trattato di un oggetto più grande avremmo probabilmente ottenuto un valore di Re talmente grande da superare il ginocchio e darci un valore di Cf che avrebbe fatto trovare una velocità di equilibrio molto alta che, pur essendo accettabile matematicamente non lo sarebbe fisicamente.