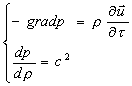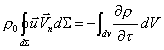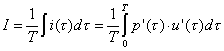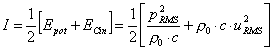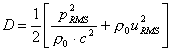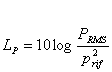Equazione di d’Alembert
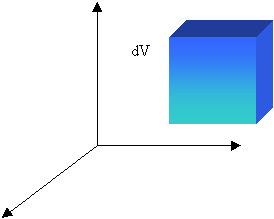
Consideriamo
un elemento cubico infinitesimale di
fluido che in un riferimento cartesiano ortogonale ha un volume dV con dV = dxdydz.
Consideriamo la LEGGE DI NEWTON, dalla quale arriveremo
alla equazione che cerchiamo.
La
legge di Newton, nota anche come la seconda legge della dinamica costituisce
l’equazione fondamentale della meccanica classica:
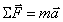 (1)
(1)
dove
SF rappresenta il vettore somma di tutte le forze agenti sul corpo, m è la sua massa e a l’accelerazione prodotta.
Applichiamo
la legge.
La
massa del fluido la conosciamo, siamo infatti in grado di stabilirla grazie alla relazione:
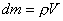 (2)
(2)
Facciamo
a questo punto una precisazione:
Abbiamo
visto che i fenomeni acustici
consistono in un trasporto di energia meccanica senza spostamento della
materia, il fluido attraverso il quale avviene la propagazione del suono si
mantiene mediamente fermo. Però nel caso in cui il volumetto di fluido è in
movimento bisogna riscrivere la seconda legge di Newton secondo una logica
lagrangiana, seguendo cioè la particella in moto: bisogna usare il concetto di
derivata sostanziale.
Nel
caso in cui il volumetto non sia fermo ma abbia una velocità u d’assieme non nulla, e sia in
movimento anche il fluido, avente cioè una velocità media di trasporto
u0 definiamo allora la velocità
acustica come lo scostamento della
velocità del volumetto da quella media del fluido:
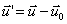 (3)
(3)
In
acustica si considera nulla la velocità media del fluido:
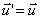 (4)
(4)
Quindi la velocità acustica coincide con la velocità
d’assieme del fluido in moto e in questo caso la derivata della velocità
rispetto al tempo, necessaria per il calcolo dell’accelerazione, deve essere
fatta in modo sostanziale cioè seguendo il moto della particella. Un esempio di
derivata sostanziale nel tempo, di una grandezza qualsiasi che assume valori
diversi in base alla posizione nel campo, potrebbe essere la seguente:
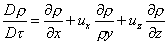 (5)
(5)
Tornando alla nostra equazione, l’unica componente che ci
manca, ovverosia l’accelerazione. L’accelerazione è definita come:
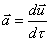 (6)
(6)
La derivata deve essere però, per quanto detto in
precedenza, fatta in modo sostanziale, anche se in acustica ciò si riduce ad
una derivata ordinaria perché la velocità del fluido, mediamente fermo, è
nulla.
Cerchiamo
a questo punto un’altra espressione per la forza dF.
Effettuiamo
a tal proposito il bilancio delle forze, cercando la risultante delle forze
agenti sul volumetto che è dato dalla somma vettoriale delle sue tre componenti
cartesiane. Consideriamo per semplicità il caso monodimensionale. Il cubetto è
compreso tra l’ascissa x in corrispondenza della quale agisce
la pressione p1=p, e
l’ascissa x+dx la cui corrispondente
pressione è data da p2=p+(¶ p/¶ x)dx.
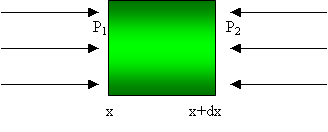
La
risultante delle forze in quella direzione è data dal prodotto della pressione
risultante in quella direzione, che è uguale alla differenza di pressione tra
le facce 1 e 2, per la superficie interessata A con A=dydz.
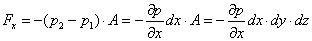 (8)
(8)
Consideriamo
ora le altre componenti della forza secondo l’asse y e z
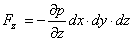 (10)
(10)
Andando a sostituire nella legge di Newton otteniamo che:
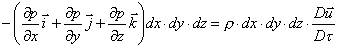 (11)
(11)
Introducendo il gradiente e semplificando ricaviamo:
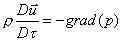 PRIMA EQUAZIONE (12)
PRIMA EQUAZIONE (12)
Il
segno meno è significativo del fatto il gradiente sia positivo nella direzione
delle pressioni crescenti mentre la differenza P2 – P1 è
positiva nella direzione opposta, dal punto di vista fisico il significato del
meno è che i fluidi hanno la tendenza ad andare verso le zone a pressione
minore.
Mi
serve una seconda equazione.
Vogliamo
conoscere la dipendenza della densità r del fluido dalla pressione.
Introduciamo le cosiddette approssimazioni di Boussinesq
(Valentin Joseph Boussinesq, 1842-1929, matematico francese):
Nel caso del campo acustico vengono fatte le
seguenti semplificazioni legate alle caratteristiche intrinseche del campo
stesso:
1.
La
derivata sostanziale della velocità diventa una derivata ordinaria perché il fluido
è mediamente fermo.
2.
Ipotesi
di piccole oscillazioni.
In particolare la ipotesi di piccole oscillazioni mi
permettono di fare due importanti semplificazioni:
·
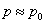
·
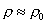
Questo
perché in queste ipotesi p0>>p’
e r0>>r’
Dove p’ la
pressione acustica o meglio lo scostamento da quella media all’equilibrio ed è
l’unica responsabile del movimento del volumetto di fluido; p0 è la pressione media
atmosferica, costante in ogni punto del volumetto in assenza di suono e che
quindi non contribuirebbe al suo moto.
r ’ è la variazione di densità
del mezzo perturbato rispetto alla situazione di equilibrio; r 0 è la densità media, prima
della sollecitazione acustica.
Nelle
ipotesi di piccole oscillazioni infatti i fenomeni acustici perturbano il mezzo
coinvolto ma di poco cioè la variazione delle grandezze fisiche del mezzo da
una situazione di equilibrio, prima della sollecitazione acustica, ad una
perturbata, è piccola.
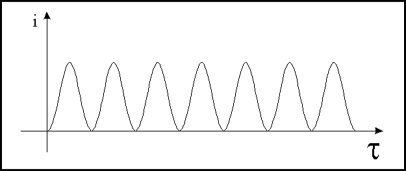
Consideriamo la situazione schematizzata nel grafico sottostante.
Applichiamo attraverso il pistone una pressione che
determina un aumento della densità.
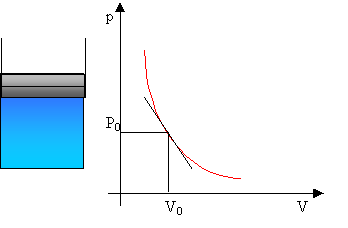
Sia (p0,V0) il punto di
equilibrio, e sia r la retta tangente alla curva nel punto di equilibrio. Applicando una
pressione p’ al gas, il sistema oscilla avanti e indietro lungo la retta r.
Sapendo,
dalla legge di Poisson, che pVg=cost, cerchiamo la retta
tangente alla curva nell’intorno del punto (p0, V0)
derivando l’espressione:
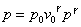 (13)
(13)
Otteneniamo:
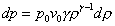 (14)
(14)
Cerchiamo,
a questo punto di semplificare l’equazione precedente:
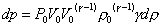 (15)
(15)
Ricordando
che v0 è il reciproco di r0 cioè:
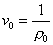 (16)
(16)
E che:
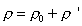 (17)
(17)
Ma,
per le semplificazioni viste in precedenza, possiamo scrivere:
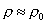 (18)
(18)
Otteniamo
quindi:
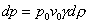 (19)
(19)
Introduciamo
l’equazione dei gas perfetti, equazione che mi servirà per arrivare
all’equazione di d’Alembert.
Il
gas perfetto è un modello ideale di stato fisico della materia caratterizzato
dal fatto che in esso sono nulle le forze fra le molecole ed il volume
effettivo di queste è trascurabile rispetto al volume occupato dall’intera
massa gassosa.
Per
qualunque sistema si possono definire le tre variabili, pressione P, volume V e
temperatura T, che si riferiscono direttamente allo stato del sistema (
indirettamente anche alla sua composizione) e perciò vengono chiamate variabili
di stato. Esse sono fra di loro indipendenti, ma esiste una relazione
funzionale, denominata equazione di stato che esprime la dipendenza di ciascuna
di esse dalle altre due e dal numero di mole n:
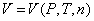
Questa
equazione prende anche il nome di equazione caratteristica e nel caso del gas
perfetto ha la forma semplice:
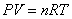 (20)
(20)
Quindi
abbiamo che:
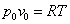 (21)
(21)
Sostituendo
nell’equazione trovata in precedenza otteniamo:
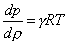 (22)
(22)
Ricordandoci
che la velocità c del suono è uguale
a:
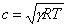 (23)
(23)
e
sostituendo nell’equazione prima trovata:
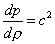 (24)
(24)
Abbiamo
quindi ricavato due equazioni differenziali.
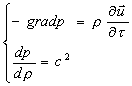 (25,26)
(25,26)

Ho tre incognite in
due equazioni, mi serve una terza
equazione.
Ammettendo che il campo delle velocità sia solenoidale e
quindi ammette potenziale, andiamo a definire una nuova grandezza chiamata
potenziale della velocità:
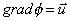 (27)
(27)
Riscriviamo
le equazioni sopra:
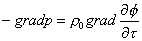 (28)
(28)
Semplificando:
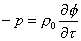 (29)
(29)
Che
rappresenta l’equazione di Eulero riscritta.
Introduciamo
l’equazione di continuità.
L’equazione di continuità non ha senso in assenza di
fenomeni di accumulo cioè quando in regime stazionario la massa del volumetto
di fluido resta costante. Questo però non è il caso dell’acustica dove
periodicamente massa entra ed esce dal volumetto in quantità diverse formando
accumuli che implicano una variazione della densità del volumetto stesso.
La variazione di densità è giustificata anche dal
fatto che dentro al volumetto varia la velocità e la pressione del fluido; se
l’aria si comporta come un gas perfetto è normale che variando la pressione
cambia anche proporzionalmente la densità.
Considerando il volumetto dV delimitato da una superficie chiusa dS orientata
in modo che il versore della normale vn
sia in ogni punto diretto verso l’esterno e facendo un ragionamento analogo a
quello fatto per le forze, abbiamo:
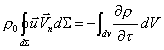 (30)
(30)
da cui, applicando il teorema della divergenza in
base al quale il flusso di un campo attraverso una superficie chiusa dS è uguale all’integrale della
divergenza del campo esteso al volume racchiuso da dS ,
otteniamo:
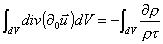 (31)
(31)
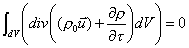 (32)
(32)
Dovendo
essere valida questa relazione comunque si scelga il volume dV, deve essere nullo l’integrando
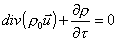 (33)
(33)
otteniamo:
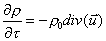 (34)
(34)
Utilizzando
l’equazione di continuità e possiamo scrivere che:
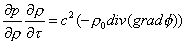 (35)
(35)
Sostituendo
a p nell’equazione precedente
l’espressione sotto:
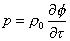 (36)
(36)
Otteniamo:
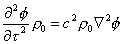 (37)
(37)
Da
cui semplificando r0 è facile ottenere
l’Equazione di d’Alembert:
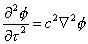 (38)
(38)
Detta
anche equazione delle onde acustiche
Data
la sua complessità l’equazione di d’Alembert nella pratica si integra solo in
tre casi:
-
ONDA PIANA PROGRESSIVA
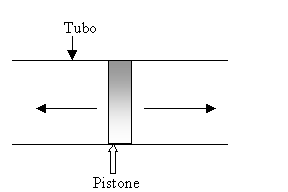
E’
quell’onda che si sviluppa all’interno di un tubo di lunghezza indefinita,
quando il fluido contenuto al suo interno viene sollecitato da un pistone che
si muove di moto armonico
-ONDA
SFERICA PROGRESSIVA
Generata da una sorgente sonora di forma sferica che
irradia in ogni direzione il suono.
-ONDA
PIANA STAZIONARIA
E’
quell’onda che si sviluppa all’interno di un tubo di lunghezza finita quando il
fluido viene sollecitato da un pistone che comprime il fluido periodicamente.
A
parte questi tre casi l’equazione di d’Alembert non si integra; esistono però
in casi geometrici complessi svariati programmi di calcolo che sfruttano dei
metodi numerici come gli elementi finiti o gli elementi di contorno e ci
forniscono la soluzione dell’equazione.
Intensimetro
L’intensimetro è uno strumento utilizzato in ambito
acustico per misurare l’intensità del suono, o meglio la sua velocità. E’ costituito da una coppia di
microfoni posizionati lungo la direzione nella quale vogliamo determinare la
velocità del suono. I microfoni misurano la pressione delle particelle del
campo sonoro, da cui ricaviamo l’intensità del suono in quella specifica
direzione.
Nel
nostro caso vogliamo misurare la componente cartesiana della velocità lungo
l’asse x. Posizioniamo quindi , ad una distanza reciproca d, una coppia di microfoni destinati a misurare le pressioni sonore
p’1 e p’2.
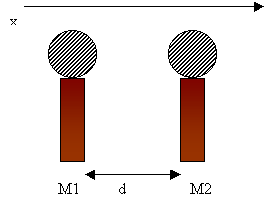
Una sola coppia di microfoni riesce a misurare una sola
componente cartesiana della velocità; volendo misurare la velocità complessiva
nelle sue tre componenti cartesiane posizionerò altre due coppie di microfoni
nelle altre due direzioni.
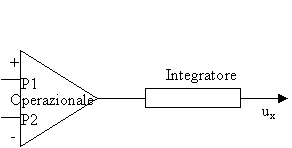
Le uscite dei microfoni vengono collegate ad un
operazionale a sua volta collegato ad un integratore, il quale darà in uscita
un segnale proporzionale alla componente cartesiana della velocità associata
alla direzione nella quale sono posizionati i microfoni.
Lungo la direzione x il gradiente della pressione viene
approssimato con una differenza finita fra le pressioni nei due punti, lecita
se la distanza d fra i microfoni è piccola (situazione che nella pratica
si cerca di realizzare):
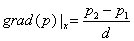 (39)
(39)
Calcoliamo
adesso la componente della velocità nella direzione x.
La
determiniamo a partire dall’equazione di Eulero e tenendo conto dell’equazione
sopra scritta.
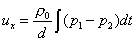 (40)
(40)
Quello
che voglio è però l’intensità del suono nella direzione x. Ma io so che:
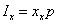 (41)
(41)
E
che la pressione media tra i microfoni è:
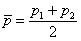 (42)
(42)
Nell’ipotesi
che il segnale sia sinusoidale:
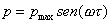 (43)
(43)
si
ha:
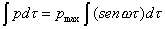 (44)
(44)
ottenendo:
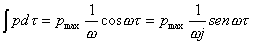 (45)
(45)
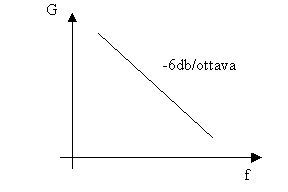
Se
i segnali in uscita dai microfoni vengono campionati, lavorando numericamente
l’integrale può essere realizzato con una semplice somma dei campioni del
segnale differenza di pressione; restando invece in ambito analogico si può
dimostrare che fare un’integrazione nel tempo equivale nel dominio della
frequenza a far attraversare al segnale un filtro analogico con un guadagno che
cala linearmente con la frequenza:
Onde
piane progressive
Facciamo
a questo punto un’analisi delle onde piane progressive cercando in particolare
le espressioni della:
·
velocità;
·
pressione;
·
intensità;
·
impedenza;
a partire dalla soluzione dell’equazione di
D’Alembert espressa in termini del potenziale F .
Un’onda piana e progressiva è un’onda in cui tutte
le particelle si muovono in un’unica direzione con la stessa velocità e
pressione.
Come
sorgente di queste onde possiamo pensare ad un pistone che si muove avanti e
indietro all’interno di un tubo lungo una direzione di moto armonico.
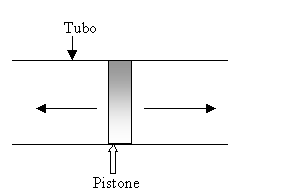
Poniamoci
nelle ipotesi che al tempo t=0:
·
Spostamento s =
0
·
Velocità u =u max
La
soluzione dell’equazione di D’Alembert nel caso dell’onda piana progressiva è
una funzione di tipo armonico:
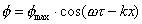 (46)
(46)
dove
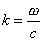 (47)
(47)
rappresenta
il NUMERO D’ONDA
dove w è la velocità angolare del
pistone.
La
formula di EULERO ci permette a questo punto di esprimere il potenziale della
velocità in notazione complessa.
Io
so che:
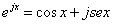 (48)
(48)
da
cui:
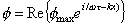 (49)
(49)
dove j rappresenta l’unità immaginaria.
Generalmente si tende ad omettere l’indicazione
della parte reale della grandezza esponenziale solo per comodità,
sottintendendo che soltanto la parte reale ha significato in un contesto
fisico.
Scriviamo quindi:
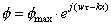 (50)
(50)
Nel contesto geometrico nel quale ci siamo messi,
ovverosia il pistone che si muove di moto armonico all’interno del tubo nella
sola direzione x il gradiente si riduce alla sola derivata direzione lungo x,
in quanto le grandezze variano soltanto nella direzione dell’asse x quindi:
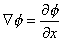 (51)
(51)
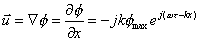 (52)
(52)
è chiaro che di questa espressione a noi interessa
soltanto la parte reale in quanto la parte immaginaria non ha significato
fisico. Il valore -j indica che la
velocità è sfasata di -p /2 rispetto al potenziale e quindi se quest’ultimo è una grandezza
cosinusoidale, la velocità sarà una grandezza sinusoidale.
A
questo punto ricordandoci delle condizioni al contorno, viste in precedenza
ricaviamo fmax
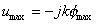 (53)
(53)
Da cui:
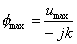 (54)
(54)
Quindi sostituendo la (53) nella (54) e
semplificando si ottiene:
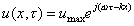 (55)
(55)
Passiamo adesso al calcolo della pressione.
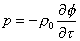 (56)
(56)
sostituendo ricaviamo:
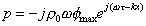 (57)
(57)
definendo:
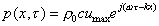 (58)
(58)
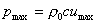 (59)
(59)
ricordandoci della (55) possiamo scrivere:
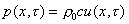 (60)
(60)
Calcoliamo
l’intensità istantanea.
Sappiamo
che:
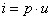 (61)
(61)
quindi
sostituendo:
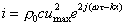 (62)
(62)
Dall’intensità sonora istantanea si può ricavare
l’intensità sonora media calcolando la media nel tempo del valore istantaneo:
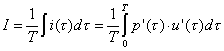 (63)
(63)
Quindi,
nel nostro caso:
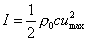 (64)
(64)
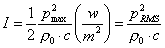

(65)
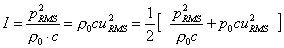 (66)
(66)
Se pressione e velocità sono segnali sinusoidali in
fase , sono cioè campi sincroni, abbiamo il massimo trasferimento di energia
possibile e possiamo approssimare abbastanza bene l’intensità con il quadrato
della pressione in quanto pressione e velocità sono sostanzialmente lo stesso
segnale a meno di una costante moltiplicativa (questa approssimazione oggi non
è più molto usata poiché pressione e velocità devono essere in fase per avere
una buona stima; in passato, invece, era l’unico modo per dare una
rappresentazione matematica dell’intensità sonora in quanto non vi erano
strumenti in grado di misurare la velocità delle particelle).
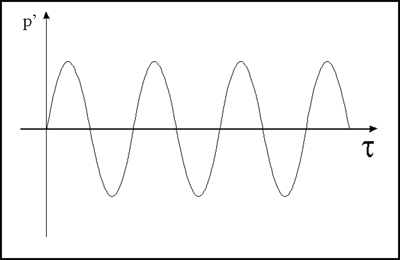
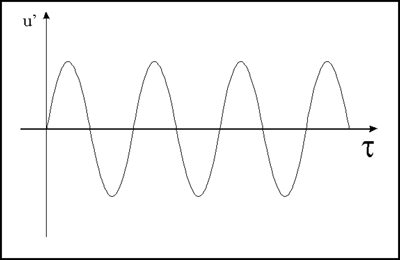
Passiamo
all’impedenza.
L’impedenza
acustica è una grandezza di notevole importanza ed è definita come:
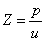 (67)
(67)
In generale l’impedenza dovrebbe dipendere dal tempo
visto che sia pressione che velocità sono funzioni del tempo. Però sia p che u sono segnali che copiano la stessa forma d’onda di partenza e
quindi il loro rapporto non dipende dal tempo ma solo dal punto del campo
sonoro in cui lo vado a calcolare.
L’unità di misura dell’impedenza è Pa / (m/s) a cui è stato dato il nome Rayl in onore di John William Strutt
Rayleigh (1842-1919, fisico inglese, studioso di ottica, meccanica e acustica a
cui è stato dato il premio Nobel per la fisica nel 1904 per gli studi compiuti
con Ramsay che portarono alla scoperta dell’argo, il primo gas nobile
identificato).
L’impedenza dell’aria in condizioni normali è di
circa 415Rayl.
Calcoliamo l’impedenza per l’onda piana progressiva
ricavandola dalla (60) ottenendo:
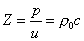 (68)
(68)
Quindi tra U e c vale la seguente relazione:
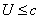
L’uguaglianza vale soltanto nel
caso delle onde piane progressive.
quanto più è reattivo il nostro corpo tanto più
questo indice è grande.
A volte
viene indicato l’indice di reattività come la differenza tra il livello
di pressione e quello di intensità :
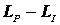
ma questo è un errore visto che questa differenza potrebbe essere negativa ,e ciò
indicherebbe che un campo si possa propagare più velocemente di un onda piana
progressiva, ma questo è impossibile.