Il secondo principio della termodinamica
Anergia ed exergia
La legge sulla conservazione dell’energia e’ uno dei pilastri della
fisica classica. E’ noto infatti che un generico oggetto possa acquistare
o cedere indistintamente all’ambiente energia (cinetica, chimica, potenziale,
elastica), a condizione che il bilancio complessivo non violi la suddetta
legge.
Anche il primo principio della termodinamica esprime il concetto di conservazione dell’energia:
?U=Q-L
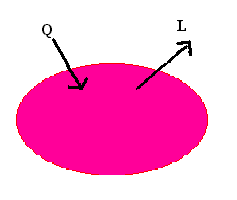
Figura 1. Convenzione dei segni per l'energia scambiata da un sistema chiuso (la freccia indica il verso positivo).
Ai fini economici pero’ non e’ vero che tutte le forme di energia sono equivalenti: per esempio l’energia immagazzinata nell’acqua calda non risulta preziosa come il lavoro meccanico.
Elenchiamo quindi i vari
tipi di energia in ordine d’importanza:
-ENERGIA ELETTRICA
-ENERGIA MECCANICA
-ENERGIA CHIMICA
…
.CALORE
Per capire il criterio con cui e’ stata impostata questa scaletta bisogna dare le seguenti definizioni:
ANERGIA= energia non convertibile in lavoro.
EXERGIA=
energia convertibile in lavoro.
Il lavoro meccanico e’ 100% exergia. Le altre forme di energia sono convertibili in lavoro solo per una certa percentuale.
Supponiamo di avere un quantitativo energetico complessivo di 1000J. Graficamente si può rappresentare il legame tra anergia ed exergia nel seguente modo.
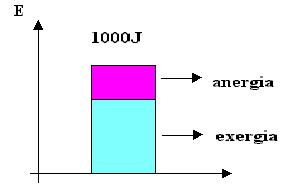
Figura 2. Partizione dell'energia.
Esempi:
- L’energia elettrica ha il 99% di exergia e l’1% di anergia
- L’energia chimica ha l’80% di exergia e il 20% di anergia (alta percentuale dovuta alle perdite di calore che si manifestano durante le reazioni)
L’ENERGIA TERMICA
I
combustibili più utilizzati per sfruttare l’energia termica sono
il carbone, il petrolio e il gas naturale, tutti composti presenti in natura.
Essi vengono fatti reagire con l’aria affinché l’energia chimica
della reazione si trasformi in energia termica.
REAZIONE ESOTERMICA
COMBUSTIBILE + ARIA = C02 + H2O
Dove l’aria e’ costituita dal 21% di ossigeno ed il 79% di azoto.
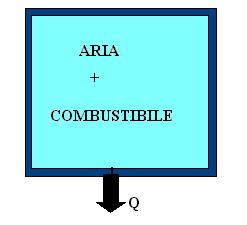
Figura 3. Recipiente adiabatico
E’ un sistema chiuso, l’energia interna rimane invariata. Inizialmente possiede energia chimica.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabella 1. I poteri calorifici
Il
bilancio dell’energia prima e dopo la reazione si può esprimere
nel seguente modo:
![]() (1)
(1)
Con Ec = MCOMB * PCAL,COMB
UF=
energia interna dei fumi
Inoltre
per la legge della conservazione della massa : MF
= MA +
MCOMB
Sostituendo i valori delle energie interne ottengo…
![]() (2)
(2)
Dove con CV si intende la capacità termica a volume costante, ovvero la quantità di energia necessaria ad innalzare di un grado la temperatura della sostanza.,
T2, denominata anche temperatura adiabatica, e’ molto elevata e si aggira attorno ai 1400-1900 °C.
Si
fa’ reagire una quantità di aria stechiometrica, di modo che partecipi
tutta alla reazione, senza che rimangano molecole di ossigeno. Se invece
avessimo una quantità di ossigeno inferiore a quella richiesta ci
sarebbe la formazione di sostanze inquinanti, come il monossido di carbonio.
Per evitare la formazione di CO si fornisce un eccesso di aria, tanto più
necessario quanto più e’ scadente il combustibile. Un altro metodo
per sviare questo inconveniente sarebbe fare avvenire la reazione al di
fuori della camera di combustione ma inevitabilmente si causerebbe una
dispersione di energia.
Una volta avvenuta la reazione all’interno del recipiente adiabatico ottengo la massa di fumi MF alla temperatura adiabatica. Piano piano si lascia fluire al di fuori il calore prodotto, lasciando inalterato il quantitativo di massa. Il processo si può rappresentare nel seguente modo.
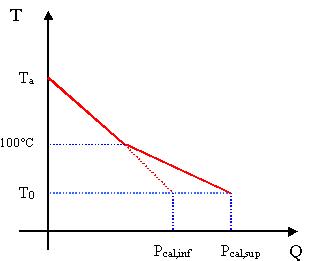
Figura 4. Rappresentazione della variazione di temperatura all’ interno del recipiente adiabatico in funzione del calore ceduto
La caratteristica calore-temperatura e’ rappresentata da una spezzata poiché a 100°C si inizia a condensare il vapore e il cambiamento di fase libera dell’energia (CALORE LATENTE). Se invece la capacita’ termica fosse costante avrei un’unica retta.
Sull’asse delle ascisse sono stati messi in evidenza due punti importanti: il potere calorifico inferiore (che non tiene conto del cambiamento di stato) e il potere calorifico superiore. Il potere calorifico e’ la quantità di calore che bisogna sottrarre per riportare il sistema alla temperatura ambiente. Di primo acchito il potere calorifico inferiore potrebbe sembrare solo una cattiva approssimazione che non tiene conto di importanti aspetti fisici del sistema; in verità quando non c’e’ presenza di acqua (es: terra antracite) si discosta poco dal valore reale.
Nelle applicazioni pratiche inoltre si e’ soliti utilizzare il potere calorifico inferiore.
RENDIMENTO DELLA MACCHINA TERMICA
![]()
Ef,serv=
energia dei fluidi di servizio
Il rendimento può essere maggiore di1 quando si ha della condensazione di vapore. In primis sembrerebbe un assurdo ? > 1 ma nella termodinamica ci sono molte apparenti contraddizioni.
Un tempo si erano vietate le macchine con ? > 1 perché si pensava inquinassero di più. Per dimostrare questa infondata teoria ponevano un lenzuolo bianco nelle vicinanze della macchina termica e poi ne analizzavano il residuo. Ovviamente in caso di condensazione i detriti appesantiti dall’acqua ricadevano immediatamente sul

Figura 5. Esempi di ciminiere
IL
SERBATOIO DI CALORE
Nella prima meta’ dell’800 era ancora diffuso il concetto di calorico, un magico fluido fautore della trasmissione di calore tra i corpi. Il corpo più caldo conteneva una quantità maggiore di calorico rispetto al corpo più freddo e quindi era in grado di cederlo a quest’ultimo, per mantenere l’equilibrio termico.
Questo concetto fu abbandonato grazie a Carnot, fisico francese, ed i suoi studi sulla termodinamica. Egli si occupava di macchine a vapore ed era stupito del fatto che la macchina termica perfetta non poteva esistere.
Per portare avanti i suoi studi utilizzo’ il serbatoio di calore: esso e’ un sistema chiuso che riesce a scambiare una certa quantità di calore con l’esterno mantenendo la temperatura costante.
Schematicamente…
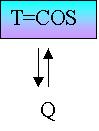
Figura 6. Schematizzazione di un serbatoio di calore
In un recipiente colmo d’acqua pongo dei cubetti di ghiaccio. Questo sistema e’ in equilibrio alla temperatura di 0°C. Se proviamo a prelevare calore, vediamo che si forma un po’ di ghiaccio, invece se forniamo calore ne’ fonde una parte. Tutto questo avviene a temperatura costante.
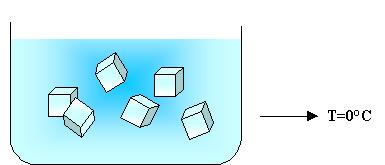
Figura 7. Esempio di serbatoio di calore
Si suppone che questo serbatoio sia infinitamente grande per poter scambiare calore con l’esterno a piacere senza risentire di variazioni termiche.
Considero
2 serbatoi di calore a temperature diverse e li collego lasciando fluire
il calore. Un esempio pratico di questo procedimento ci e’ dato dai termosifoni
delle nostre case, dove il calore fluisce dall’acqua all’aria
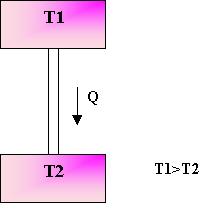
Figura 8, Schematizzazione dello scambio di calore tra due serbatoi
Per mantenere i serbatoi a temperatura costante si fa’ spesso uso di termostati anche se imponendo la temperatura limitiamo il rendimento della macchina termica.
A questo punto bisogna definire che cos’e’ una macchina ciclica.
Una macchina ciclica e’ una macchina a fluido che ritorna periodicamente al suo stato di partenza e quindi presenta variazioni di energia interna nulle sul periodo (?U=0).
Esempi
di macchine cicliche possono essere:
- Una pompa da bicicletta
- Motore a scoppio
- Motore a diesel
- Locomotiva a vapore
- Caldaia a vapore
- …
Una macchina termica invece e’ un apparato che converte calore in lavoro e viceversa.
Per mantenere i serbatoi a temperatura costante si fa’ spesso uso di termostati anche se imponendo la temperatura limitiamo il rendimento della macchina termica.
A questo punto bisogna definire che cos’è una macchina ciclica.
E’ una macchina a fluido che ritorna periodicamente al suo stato di partenza e quindi presenta variazioni di energia interna nulle sul periodo (?U=0).
Esempi
di macchine cicliche possono essere:
- Una pompa da bicicletta
- Motore a scoppio
- Motore a diesel
- Locomotiva a vapore
- Caldaia a vapore
- …
Una
macchina termica invece e’ un apparato che converte calore in lavoro e
viceversa.
MACCHINA TERMICA CICLICA
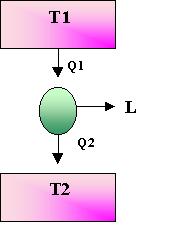
Figura 9. Schematizzazione della macchina termica ciclica
La macchina termica ciclica e’ costituita da un serbatoio caldo che possiamo identificare con la caldaia, un serbatoio freddo ( l’ambiente) ed un motore.
Maggiore
e’ il salto termico tra T1 e T2 ,tanto maggiore sarà il passaggio
di calore.
2° PRINCIPIO DELLA TERMODINAMICA (ENUNCIATO DI KELVIN-PLANK)
Il
secondo principio della termodinamica afferma che in un processo ciclico
non e’ possibile convertire interamente calore in lavoro senza che avvenga
una variazione nell’ambiente. Secondo la figura n. la variazione dell’ambiente
e’ rappresentata da Q2, ovvero il calore ceduto. Quindi e’ impossibile
costruire una macchina termica con rendimento unitario poiché Q2
non può mai essere nullo. Questo limite non ha niente a che vedere
con le dispersioni accidentali di energia che si riscontrano in ogni apparecchiatura,
ma e’ dato dai principi fisici stessi. Infatti la macchina termica ideale
non ha senso di esistere nemmeno dal punto di vista teorico.
CICLO DI CARNOT
Suppongo di avere un cilindro
dotato di pistone mobile all’interno del quale c’e’ del gas.
- Inizialmente pongo il cilindro a contatto con il serbatoio T1 a temperatura elevata. Il gas assorbe il calore Q1 ma dal momento che e’ libero di espandersi, rimane alla stessa temperatura senza variare la sua energia interna. E’ una trasformazione isoterma e tutto il calore viene trasformato in lavoro (L= forza che alza il pistone per lo spostamento del pistone stesso).
- Successivamente isolo il cilindro dal serbatoio T1 e lascio ancora espandere il gas. Non ho scambio di calore con l’esterno quindi il lavoro compiuto va’ a scapito dell’energia interna. In seguito a questa trasformazione adiabatica il gas si ritrova alla temperatura T2, inferiore rispetto a T1.
- Ora pongo il cilindro in contatto con il serbatoio T2 a bassa temperatura e spingo il pistone verso il basso, aumentando cosi’ la pressione del gas. Dal momento che questa e’ una trasformazione isoterma, non ho variazione dell’energia interna ma soltanto cessione del calore Q2 da parte del gas al serbatoio T2.
- Infine isolo di nuovo il serbatoio per attuare una trasformazione adiabatica. Comprimendo il pistone compio lavoro sul gas e lo porto alla temperatura T1. In questo modo sono tornata al punto di partenza.
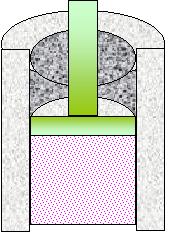
Figura 10. Sezione del cilindro utilizzato per studiare il ciclo di Carnot
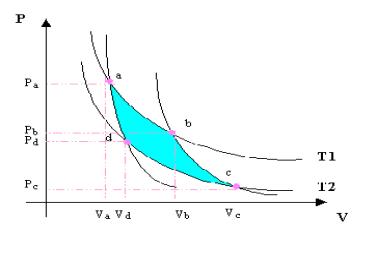
Figura 10. Diagramma pV del ciclo di Carnot.
Una simulazione dell’andamento del ciclo di Carnot si puo’ trovare all’indirizzo:
http://www.phy.ntnu.edu.tw/java/carnot/carnot.html
TEOREMA DI CARNOT
Si definisce
coefficiente economico ?
di un ciclo il lavoro totale fatto sull’ambiente circostante diviso per
il calore totale assorbito Q1.
![]() (3)
(3)
Dal momento che L=Q1-Q2 posso apportare le seguenti sostituzioni:
![]() (4)
(4)
Per il secondo principio ? non può mai essere pari a 1.
Si può facilmente dimostrare che il rendimento di una macchina di Carnot dipende solo dalle temperature dei due serbatoi tra i quali essa opera.
Dal momento che la macchina e’ ciclica la variazione dell’energia interna del sistema e’ nulla. Quindi per il primo principio della termodinamica il calore Q1 trasferito dal serbatoio ad alta temperatura e’ uguale in modulo al lavoro L.
Di conseguenza…
![]() (5)
(5)
Analogamente per la trasformazione cd della figura posso scrivere
![]() (6)
(6)
Per le due trasformazioni adiabatiche lungo bc e da vale la formula:
![]() (7)
(7)
![]() (8)
(8)
Facendo
il rapporto delle due uguaglianze ottengo:
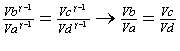 (9)
(9)
Facendo
il rapporto tra Q1 e Q2 e considerando i precedenti risultati ottengo:
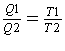 (10)
(10)
Percio’:
![]() (11)
(11)
Il rendimento aumenta al diminuire di T2 come era intuitivamente prevedibile.
Esempio.
Supponiamo di avere una caldaia alla temperatura di 250°C e l’ambiente esterno e’ ad una temperatura di 20°C.
Il rendimento risulta essere:
![]()
Tutte
le macchine termiche reversibili hanno il coefficiente economico di Carnot.
LA MACCHINA TERMICA INVERSA
La macchina termica inversa e’ la macchina frigorifera. Assorbe calore dal serbatoio T2 a temperatura bassa e lo cede al serbatoio T1, maggiore di T2. Dal momento che il calore non può fluire spontaneamente per l’enunciato di Clausius da un serbatoio a bassa temperatura ad uno ad alta temperatura, e’ necessario un motore che compie lavoro sul sistema. Fornendo quindi energia sottoforma di lavoro e’ possibile questo passaggio.
Come avevamo fatto per la macchina termica semplice anche per la macchina frigorifera possiamo definire un coefficiente di rendimento.
![]() (12)
(12)
Quando ? e’ grande ?f e’ piccolo e viceversa.Una macchina frigorifera funziona bene se c’e’ poca differenza di temperatura tra i due serbatoi.
Definiamo invece il rendimento della pompa di calore nel seguente modo:
![]() (13)
(13)
La pompa di calore viene utilizzata ai fini del riscaldamento e risulta piu’ efficiente di tutti i metodi a combustibile. E’ una macchina che richiedendo dall’esterno una potenza L permette di trasferire all’interno dell’abitazione il calore Q1=L+Q2. Tanto maggiore sarà il calore Q2, minore sarà il lavoro L richiesto a beneficio quindi del buon rendimento della macchina. La pompa di calore e’ conveniente anche ai fini ecologici poiché sottraendo calore all’ambiente limitiamo il surriscaldamento del pianeta.
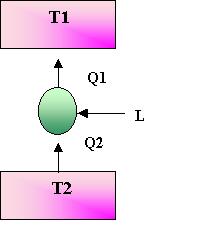
Figura 11. Schematizzazione di una macchina frigorifera
ENUNCIATO DI CLAUSIUS DEL 2° PRINCIPIO DELLA TERMODINAMICA
Un’altra formulazione del 2° principio della termodinamica e’ l’enunciato di Clausius, basato sull’efficienza della macchina frigorifera.
Non e’ possibile un processo ciclico nel quale il calore fluisca da un corpo a un altro a temperatura maggiore senza che null’altro accada
Affinché il calore possa fluire in questo verso bisogna compiere lavoro dall’esterno perché spontaneamente il calore andrebbe nel verso opposto.
Quindi l’enunciato di Clausius
afferma che non esistono frigoriferi perfetti.
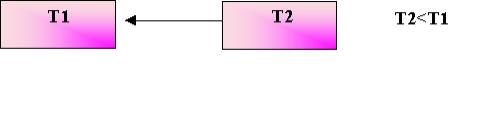
Figura 12. Schema di una macchina frigorifera perfetta
Nei frigoriferi domestici il serbatoio freddo e’ la cella e il serbatoio caldo l’ambiente in cui e’ posto l’elettrodomestico. Il lavoro esterno e’ compiuto da un motore.
Di primo acchito gli enunciati di Kelvin-Plank
e di Clausius sembrano indipendenti l’uno dall’altro ma in verità
sono assolutamente equivalenti. Infatti, ragionando per assurdo e negando
la validità di uno, si arriva inevitabilmente alla negazione anche
dell’altro.
UGUAGLIANZA DEGLI ENUNCIATI DI CLAUSIUS E DI KELVIN-PLANK
Suppongo inizialmente falso l’enunciato di Kelvin-Plank. Quindi ammetto l’esistenza della macchina termica perfetta capace di convertire tutto il calore in lavoro senza scambi con il serbatoio freddo. Ora penso di utilizzare questo lavoro per far funzionare una macchina frigorifera reale. Il frigorifero assorbe il calore Q2 dal serbatoio a temperatura più bassa e cede il calore Q1=Q2+Lal serbatoio a temperatura maggiore.
Complessivamente non e’ stato fatto alcun lavoro perché il lavoro fatto dalla prima macchina termica viene assorbito completamente dalla seconda macchina termica.
Perciò la macchina
complessiva si comporta come un frigorifero perfetto. Questo vuol dire
che se posso costruire un motore perfetto posso costruire anche un frigorifero
perfetto: la violazione dell’enunciato di Kelvin-Plank implica la violazione
dell’enunciato di Clausius.
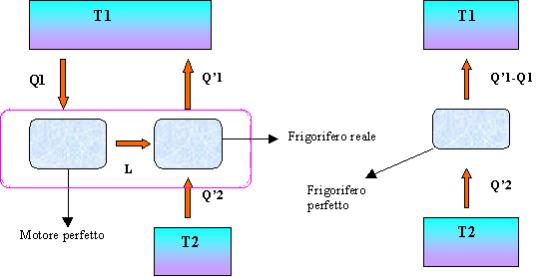
Figura 13. Un frigorifero reale azionato da un motore perfetto equivale ad un frigorifero perfetto
Seguendo lo stesso procedimento posso dimostrare che negando l’enunciato di Clausius nego anche quello di Kelvin-Plank. Suppongo quindi possibile l’esistenza del frigorifero perfetto, ovvero di una macchina termica capace di trasportare calore dal serbatoio più freddo a quello più caldo senza che sia fatto lavoro dall’esterno.
Ma allora possiamo collegare una macchina termica reale che possa comunicare con i due serbatoi di modo che il serbatoio caldo e’ sfruttato per avere lavoro e il calore Q2 e’ ceduto al serbatoio freddo. Ma allora complessivamente la quantità di calore Q2 viene fornita dal serbatoio più freddo verso il serbatoio più caldo e poi viene fornita nuovamente al serbatoio stesso.
Risulta dunque che la macchina termica produce lavoro
solo per effetto dell’arrivo della quantità di calore Q1 dal serbatoio
più caldo. Dal momento che non ci sono dispersioni di calore Q2
posso affermare di avere costruito una macchina termica perfetta, negando
l’enunciato di Kelvin-Plank.
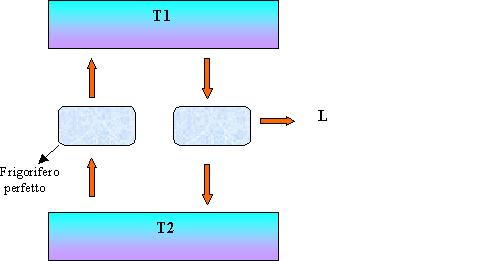
Figura 14. Un motore reale azionato da un frigorifero perfetto equivale
ad un motore perfetto.
APPENDICE
Storia
delle macchine termiche
Le prime macchine a vapore furono usate da sempre, persino da Erone di Alessandria intorno al 100 A.C per sbalordire le persone aprendo le porte come se fosse un dio. Poi si susseguirono Papin nel 1690 e Savery,che con la sua macchina obbligava l’acqua a salire in un cilindro entro miniera era poi spinta ancora più in alto ed espulsa mediante un violento getto di vapore. Questa prima pompa a vapore era costituita da 2 cilindri uno dei quali si riempiva e l’altro si svuotava. Con vapore a bassa pressione non era efficiente e questo fu il suo limite. Le caldaie, i tubi e i cilindri dell’epoca, essendo saldati con stagno, non erano in grado di resistere alle forti pressioni richieste per spingere l’acqua alle altezze utili per le miniere.
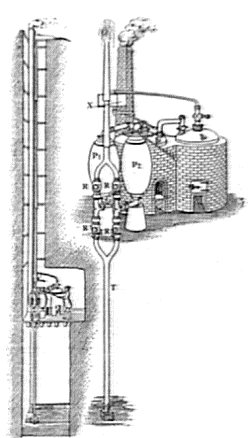
Figura 15. La macchina di Savery
Nonostante molti sforzi per migliorarla, la macchina di Savery fu ben poco impiegata e ben presto abbandonata.
In seguito Newcomen miglioro’ la macchina di Savery. Nella sua invenzione c’e’la prima importante separazione di funzioni: la caldaia e’ separata dal cilindro, che funge ancora da condensatore. Tale caldaia produceva calore alla pressione atmosferica, il bilanciere vibrava 12 volte al minuto e ad ogni corsa lo stantuffo della pompa aspirava 45 litri di acqua che venivano poi sollevati a 46 metri di altezza. La potenza delle macchine era circa 5,5 cavalli vapore. La salita del pistone della macchina (fase passiva) era dovuta alla discesa della pesante asta dello stantuffo della pompa (dall’altra parte del bilanciere). Il vapore che era immesso nel cilindro serviva esclusivamente a fare il vuoto sotto il pistone mediante condensazione prodotta con un getto di aria fredda. Il vuoto risultante consentiva alla pressione atmosferica di spingere lo stantuffo verso il basso (fase attiva) con conseguente salita del pistone della pompa. L’acqua di condensazione veniva espulsa attraverso un tubo e una valvola a chiusura idraulica. Il difetto principale di questa macchina e’ il continuo raffreddamento del cilindro che causa un enorme consumo di carbone. Il suo rendimento era solo dell’1% cioè ogni 100kg di carbone bruciati solo 1 veniva utilizzato per il pompaggio dell’acqua. Nonostante questi gravi difetti la macchina non ebbe rivali nelle Nel 1765 James Watt capì che nella macchina di Newcomen c'era in problema: l'elevata temperatura delle pareti del cilindro; ciò era dovuto al fatto che la maggior parte del calore si sprecava proprio nel riscaldamento delle pareti che poi dovevano essere di nuovo raffreddate quando si iniettava acqua fredda per condensare il vapore.

Figura 16. La macchina di Newcomen
Watt ne costruì un'altra in cui il vapore del cilindro, dopo aver spinto in su il pistone, veniva convogliato in un contenitore separato per essere condensato. Sembrerebbe quasi una sciocchezza questo accorgimento, ma fatto sta che fu un piccolo e decisivo passo per lo sviluppo delle macchine termiche ed inoltre si riusciva a compiere il doppio del lavoro della macchina di Newcomen con lo stesso combustibile; tutto questo permise a Watt di arricchirsi vendendo le sue macchine ai proprietari delle miniere. E' certo che la scoperta di Watt non si esaurì così facilmente infatti più tardi, nel 1781, brevettò i primi modelli per trasformare il moto alternativo dello stantuffo nel moto rotatorio di un albero. Da questo punto la strada si divise per dar luogo da un lato all'invenzione di Trevithick e dall'altro, con Parson, si riuscì a costruire la prima turbina a vapore che utilizzava, appunto, il vapore per produrre direttamente un moto rotatorio. "Le macchine termiche, quindi non fanno altro che trasformare energia da una forma ad un'altra e questo trasferimento è detto lavoro... il vapore si espande e compie combustibile che brucia... e si arrivò così a definire il rapporto tra il lavoro compiuto e l'energia assorbita, in altri termini si definì il rendimento di una macchina termica"
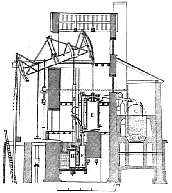
Figura 17. La macchina di Watt.
Fino al 1940 le macchine a vapore fornivano la forza motrice alla maggior parte delle locomotive utilizzate sulle linee ferroviarie, da allora, però, la costruzione di locomotive a vapore fu sospesa e i veicoli esistenti ritirati per cedere i binari a locomotive diesel che avevano un rendimento maggiore, una produttività più elevata dato che non richiedeva le fermate per il rifornimento d'acqua e di carbone.miniere inglesi per circa 60 anni.