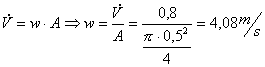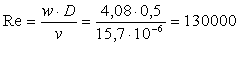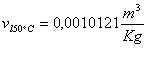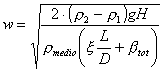Esercizio 1

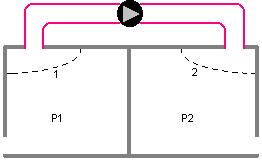
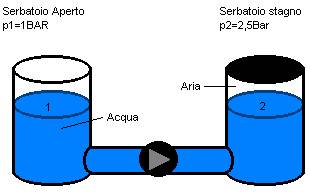
Si consideri un sistema costituito da un serbatoio aperto (che si trova perciò a pressione atmosferica) e da un autoclave (serbatoio chiuso a pressione P₂ = 2,5 bar) perfettamente stagno e pressurizzato. Tramite una pompa l’acqua deve essere portata dal primo al secondo serbatoio.

Il tubo che collega i due serbatoi ha una lunghezza L = 8m e un diametro D = 0,05m e una scabrezza relativa e/D = 0,01

Sapendo che la pompa ha un rendimento m_p = 0,6 e che la portata in massa dell’acqua deve essere costante e pari a M = 3 kg/s, calcolare la prevalenza Dp e la potenza P della pompa.

Dati:

P₁ = 1 bar

P₂ = 2,5 bar

L = 8m

D = 0,05m

M = 3 kg/s

m_p = 0,6

Soluzione:

E’ necessario, innanzitutto, scegliere nel modo più adeguato le due sezioni da utilizzare in seguito nell’equazione di Bernoulli.

Osserviamo che i peli liberi dei due serbatoi si trovano alla stessa altezza e possiamo supporre come ipotesi che essi si muovano molto lentamente tra di loro, quindi le loro velocità sono praticamente nulle.

L’equazione di Bernoulli è:

Ma nel nostro caso il lavoro è quello svolto dalla pompa quindi

e tenendo conto del fatto che e otteniamo:

Di questa equazione conosciamo le 2 pressioni ma dobbiamo ricavare dai dati il valore di R che riassume le perdite concentrate e quelle distribuite ed è dato dall’equazione:

Dove:

· = Fattore di Attrito

· L = Lunghezza del condotto

· L_e = Lunghezza equivalente (ossia dovuta alle perdite concentrate)

· w = velocità del fluido

Il fattore di attrito è ricavabile dal diagramma di Moody una volta conosciuti il Numero di Reynolds e la scabrezza relativa.

Il numero di Reynolds è dato da:

dove è la VISCOSITA’ CINEMATICA e nel nostro caso per l’acqua a 15-16°C vale .

Sapendo che la portata in massa posso ricavare la velocità del fluido

Ora possiamo ricavare il numero di Reynolds:

(E’ un moto turbolento)

Conoscendo il numero di Reynolds e la scabrezza relativa possiamo leggere dal diagramma di Moody il valore del coefficiente d’attrito .

Per finire ci mancano le lunghezze equivalenti delle perdite di carico concentrate dovute all’imbocco ed allo sbocco, esse vanno ottenute dal monogramma e risultano:

L_eq di imbocco = 0,5 m

L_eq di sbocco = 0,6 m

Possiamo ora calcolare la prevalenza:

La potenza teorica sarà quindi:

Sapendo che il rendimento della pompa m_p = 0,6 la potenza richiesta dalla pompa deve essere

Esercizio 2

Si consideri un impianto di riscaldamento costituito da un caminetto e avente le seguenti caratteristiche:

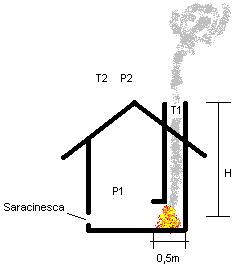
T₁=250°C

T₂=10°C

H=8m

Sapendo che in un’ora vengono bruciati circa 10 kg di legna e che per bruciarli sono necessari 14 Kg di aria possiamo ricavare la portata in massa del camino, che è pari a , essa sarà la portata in massa minima che devo avere per riuscire a bruciare tutta la legna.

Si vuole vedere se il camino “tira” e in caso positivo calcolare la velocità effettiva del processo.

Soluzione:

In prima approssimazione potrei supporre che le pressioni interne ed esterne siano uguali, in modo da semplificare i calcoli, ma ciò non è vero. E’ infatti proprio la differenza di pressione che fa tirare il camino!

Devo perciò calcolarla e utilizzo le proprietà del fluido esterno dato che quello interno è in movimento.

Devo calcolare le densità dei fumi a 10°C ed a 250°C.

OSS. Dato che nel processo di combustione la quantità d’aria che entra e 4-5 volte la quantità stechiometrica, ossia quella veramente necessaria alla combustione, posso utilizzare le caratteristiche dell’aria per calcolare le varie densità

Dall’equazione dei gas perfetti:

e considero

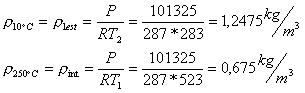
Allora la differenza di pressione risulta

L’equazione di bilancio energetico è:

lo posso considerare molto più piccola di che è la velocità di uscita dal caminetto.

Allora l’equazione diventa:

visto che ottengo:

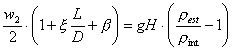
Resistenza Motore

Il membro a sinistra dell’equazione e la Resistenza che si oppone al passaggio dei fumi mentre il membro ha destra è il motore che spinge i fumi dall’interno verso l’esterno ed è dovuto alla differenza di pressione che esiste tra i due ambienti.

Sapendo che la portata in massa dei fumi deve essere pari a posso calcolare la velocità che devono avere quest’ultimi:

La sezione della canna fumaria non mi viene fornita dai dati del problema, posso perciò assumerla di forma quadrata con un lato di 0,15m che è la grandezza minima imposta dalla legge.

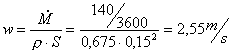
Posso ora ricavare il numero di Reynolds, sapendo che per una superficie quadrata il diametro idraulico equivale al lato e che la viscosità cinematica dell’aria a 250°C è

(moto turbolento)

La scabrezza relativa

e dal diagramma di Moody ricavo un valore per il Fattore di attrito pari a

I fumi nel loro tragitto incontrano anche un gomito che equivale ad un valore

Ora conosco tutte le grandezze che mi interessano e posso calcolare i valori della Resistenza e del Motore.

Resistenza:

Motore: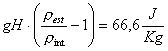

OSSERVO che il motore è sovrabbondante perciò il camino tira ma in realtà la portata in massa del camino e quindi la velocità dei fumi sarà molto maggiore di quella fornita dai dati.

Per calcolare la velocità effettiva deve utilizzare un procedimento iterattivo.

1. Calcolo la velocità partendo dal valore del motore che ho ottenuto e che varierà in base al valore del Fattore di Attrito, tramite la formula :

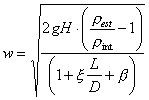
2. Dal valore di velocità ricavato calcolo il Numero di Reynolds

3. Dal numero di Reynolds calcolo il Fattore di attrito e ritorno al punto 1.

Nella tabella seguente sono riportati i risultati di qualche iterazione

w	Re	ξ	w2
5,08	18056	0,045	5,13
5,13	18255	0,043	5,19
5,19	18463	0,043	5,19

Dopo qualche iterazione la velocità si stabilizza su un determinato valore, va comunque osservato che questo valore presenta una incertezza dovuta al fatto che il calcolo del fattore di attrito ξ viene fatto per via grafica dal diagramma di Moody.

Va inoltre osservato che la velocità effettiva è due volte più grande di quella fornita dai dati perciò il camino tira molto. Questo fatto non è sempre positivo infatti l’aria calda che viene sottratta alla stanza deve essere compensata da aria fredda che proviene dall’esterno e perciò è molto più difficoltoso scaldare la stanza. Per ovviare a questo inconveniente potrei mettere una saracinesca che regoli l’aspirazione dell’aria dall’esterno verso l’interno.

Esercizio 3

Si considerino due ambienti aperti collegati tra loro da un impianto di ventilazione il quale trasporta l’aria da un locale all’altro. Si chiede di dimensionare il ventilatore calcolandone la prevalenza e la potenza.

D = 0,5 m

L = 150 m

ε = 0,5 mm

η = 0,6

Soluzione:

L’equazione di bilanciamento energetico è del tipo:

Se scegliamo le sezioni in modo opportuno, per esempio che coincidono con l’imbocco del sistema di ventilazione vediamo che le pressioni alle due sezioni sono identiche (pressione atmosferica) essendo i due locali aperti, anche le velocità sono identiche e la differenza di altezza tra le due sezioni è nulla, perciò l’equazione si semplifica notevolmente:

_{in cui:}

Dalla portata in volume del ventilatore posso ricavare la velocità dell’aria:

e quindi il Numero di Reynolds:

L’unica cosa che manca per ricavare dal Diagramma di Moody il fattore di attrito è la scabrezza relativa che risulta pari a:

Allora il fattore di attrito vale:

Il condotto di ventilazione è composto da un imbocco, da due gomiti e da uno sbocco, ognuno di questi componenti comporta una determinata perdita di carico concentrata β.

β_imbocco = 0,5

β_gomito = 1

β_sbocco = 1

Siamo ora in grado di calcolare le perdite di carico totali:

La prevalenza del ventilatore sarà quindi data da:

Perciò la potenza teorica necessaria è:

Ma visto che il nostro ventilatore ha un rendimento di 0,6 allora la potenza richiesta alla rete elettrica sarà superiore:

Esercizio 4

Determinare la potenza termica () ceduta dal corpo scaldante (termosifone) di un impianto di riscaldamento a circolazione naturale.

Un impianto a circolazione naturale è costituito da una caldaia, un termosifone e due tubi di collegamento. A differenza di un normale impianto domestico non è presente una pompa: l’acqua viene fatta circolare sfruttando la differenza di temperatura tra l’acqua uscente dalla caldaia e quella uscente dal corpo scaldante

L’unico elemento che disperde calore è il termosifone perciò i tubi mantengono inalterata la loro temperatura lungo tutto il tragitto.

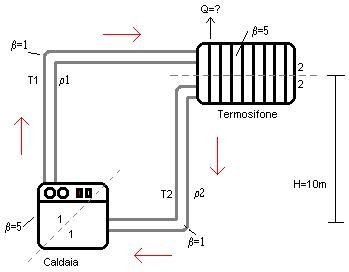
Dati:

ε = 0,0001 m (Scabrezza)

D = 0,05 m (diametro tubi)

L = 100 m (lunghezza totale dei tubi)

T₁ = 70°C

T₂ = 50°C

β_tot = 5+5+1+1 = 12

Soluzione:

Dal primo principio della termodinamica so che la potenza termica è data da:

_con

_{La portata in massa la ricavo dalla formula}

_{di cui conosco tutto a parte la velocità dell’acqua, perciò w è l’incognita da calcolare.}

Questo problema è facilmente risolvibile usando delle sezioni coincidenti e impostando due equazioni di bilancio energetico: la prima che va dalla sezione 1 alla sezione due e l’altra che va dalla sezione 2 alla 1.

E’ necessario utilizzare due densità del fluido differenti, infatti nel primo tratto l’acqua si trova a 70°C mentre nel secondo a 50°C.

Dalle tabelle del vapore dell’acqua ricavo i valori del volume specifico alle varie temperature e facendone l’inverso ottengo le densità:

da cui:

da cui:

Le equazioni di bilanciamento sono:

_{Isolando al primo membro le differenze di pressione e sommando le due equazioni si ottiene:}

_{Dato che le densità sono abbastanza simili possiamo trascurare il primo termine del secondo membro ma NON il secondo termine visto che proprio questa differenza di densità funge da motore al sistema.}

_{Per semplificare i calcoli consideriamo inoltre un valore ρmedio in modo da poter raccogliere le 2 resistenze RA e RB.}

Motore Resistenza

Da cui ricavo la velocità:

Per calcolare il valore del fattore di attrito ξ è necessario conoscere il valore numero di Reynolds ma per ricavare questo bisogna a sua volta conoscere il valore della velocità w che è proprio l’incognita. E’ necessario perciò utilizzare anche stavolta un procedimento iterattivo:

1. Scelta di un valore “sensato” di w.

2. Calcolo del numero di Reynolds.

3. Conoscendo la scabrezza relativa , si ricava il fattore di attrito ξ dal diagramma di Moody.

4. Calcolo il nuovo valore di velocità w.

5. ritorno al punto 2 fino a che i valori non si assestano attorno ad uno preciso.

Nella tabella seguente sono riportati i risultati di qualche iterazione

w	Re	ξ	w2
0,5	44706	0,026	0,179
0,179	16025	0,033	0,162
0,162	14515	0,035	0,158
0,158	14157	0,035	0,158

Alla fine la velocità si assesta attorno ad un valore approssimativo di

La portata è perciò:

e la potenza termica cercata: