UNIVERSITA’ DEGLI STUDI DI PARMA
Anno
accademico 2001-2002
Corso
di laurea : ingegneria delle telecomunicazioni
Corso
di fisica tecnica
Docente
del corso : Angelo Farina
Relazione della lezione di fisica tecnica tenuta il giorno 11/12/2001 alle ore 16 :30-18 :30
Argomenti trattati
v Scambio
termico tra due superfici piane
v Fattore
di forma
v Esercizi
sullo scambio termico
Esercizio 1
Questo esercizio studia lo scambio termico tra due superfici piane S1
e S2 poste l’una di fronte all’altra, a temperature T1 e T2
e separate dal vuoto. Esse saranno studiate nei tre casi:
1.
Entrambe le
superfici nere
2.
Una superficie
grigia, una nera
3.
Entrambe le
superfici grigie
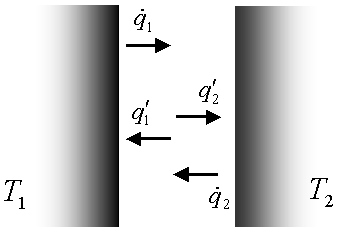
Fig. 1 – Scambio di calore tra due superfici
S1 e S2 entrambe nere
Il coefficiente di
assorbimento è pari ![]() per entrambi i corpi.
per entrambi i corpi.
Utilizzando la legge di Stefan-Boltzmann trovo
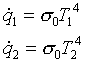 (1)
(1)
dove ricordiamo che ![]() è la costante di Boltzmann = 5.67 10-8
è la costante di Boltzmann = 5.67 10-8 ![]()
Dalla legge di Prevost (ricordando a=1) ricavo
![]() (2)
(2)
S1 grigia, S2 nera
La superficie 1 assorbe il calore ![]() e quindi riflette
e quindi riflette
![]() , che ritorna sulla superficie 2 e viene da essa assorbito
insieme alla quantità
, che ritorna sulla superficie 2 e viene da essa assorbito
insieme alla quantità ![]() emessa da 1.
emessa da 1.
![]() (4)
(4)
Da qui ricaviamo la
potenza scambiata
![]() (5)
(5)
S1, S2 entrambe grigie
Abbiamo ![]() ; chiamiamo
; chiamiamo ![]() non solo l’energia riflessa, ma tutta quella che arriva su S2,
e analogamente
non solo l’energia riflessa, ma tutta quella che arriva su S2,
e analogamente ![]() . Se risolviamo il sistema
. Se risolviamo il sistema
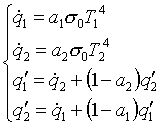 (6)
(6)
troviamo i valori che cerchiamo:
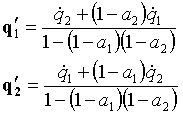
![]()
Possiamo sostituire (7) nella relazione di Prevost ![]() relativa alla
superficie S1 per trovare una equazione generale per lo scambio termico tra
due superfici grigie indefinite piane parallele, di cui le due
precedentemente trovate erano casi particolari:
relativa alla
superficie S1 per trovare una equazione generale per lo scambio termico tra
due superfici grigie indefinite piane parallele, di cui le due
precedentemente trovate erano casi particolari:
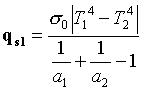 (9)
(9)
Nota: Le energie sono
parzialmente riflesse dall’una all’altra superficie, teoricamente all’infinito;
rigorosamente questo problema andrebbe risolto con un transitorio, considerando
ogni singola riflessione, ma la risoluzione tramite il bilancio energetico non
comporta un errore rilevante.
Esempio numerico
![]()
![]()
Distanza tra le lastre 0,05 m
Sostituendo nella equazione appena trovata otteniamo
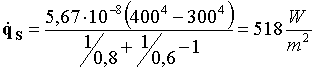 (10)
(10)
Consideriamo ora il contributo del flusso convettivo. Calcoliamo
innanzitutto il numero di Grashof:
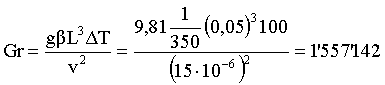 (11)
(11)
Il numero di Raleigh risulta quindi inferiore a 109 e ci
troviamo quindi in moto laminare. Calcoliamo quindi il numero di Nusselt
sostituendo a Gr il valore trovato nella (11) :
![]() (12)
(12)
e con questo possiamo trovare il coefficiente di convezione h
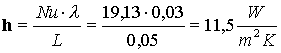 (13)
(13)
Adesso abbiamo tutto quanto ci serve per calcolare ![]()
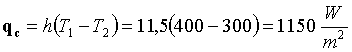 (14)
(14)
Osservazione: se avessimo alzato T1 e T2 pur
mantenendo il ![]() (ad esempio (T1=500 °C e T2=400°C), il
(ad esempio (T1=500 °C e T2=400°C), il ![]() sarebbe rimasto pressoché invariato, mentre avremmo avuto un
sarebbe rimasto pressoché invariato, mentre avremmo avuto un ![]() , cioè
, cioè ![]() diventa confrontabile con
diventa confrontabile con ![]() .
.
In una caldaia che lavora intorno ai 1550 °C, il calore scambiato per convezione rappresenta un 8-10% del calore totalmente scambiato.
Fattore di forma (o di vista)
Introduciamo questo parametro che ci permetterà di studiare lo scambio
termico tra corpi più complessi delle due superfici piane indefinite.
Presi due corpi qualsiasi che si scambiano calore, non tutta la potenza
emessa ![]() da un corpo viene
recepita dal secondo corpo, ma solo una parte di essa (che chiamiamo
da un corpo viene
recepita dal secondo corpo, ma solo una parte di essa (che chiamiamo ![]() viene assorbita e il
resto si disperde.
viene assorbita e il
resto si disperde.
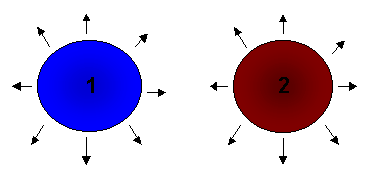
Fig. 2 – scambio termico tra due corpi qualsiasi
Definiamo quindi fattore di forma (o di vista) il rapporto tra il
calore assorbito dal corpo 2 e il calore totale emesso dal corpo 1
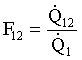 (15)
(15)
Se un corpo è completamente circondato, tutto il calore che esso emette
viene assorbito dagli altri corpi e quindi
![]() (16)
(16)
Il fattore di forma si calcola sull’ipotesi che la quantità di calore
percepita da un corpo è proporzionale all’angolo solido con cui esso viene
visto dalla sorgente. Infatti, presi due elementi di superficie S1 ed S2
di entrambi i corpi e conoscendo gli angoli solidi![]() e
e ![]() riferiti alle
rispettive superfici, è possibile calcolare
riferiti alle
rispettive superfici, è possibile calcolare
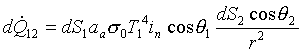 (17)
(17)
Integrando poi sulla superficie completa dei due corpi si trova ![]() da cui poi si ricava
il fattore di forma. Esistono inoltre formule che permettono di ricavare più
facilmente il valore del fattore di forma tra due superfici.
da cui poi si ricava
il fattore di forma. Esistono inoltre formule che permettono di ricavare più
facilmente il valore del fattore di forma tra due superfici.
Esercizio
Analizziamo ora uno di questi casi particolari, ossia il caso di un corpo
convesso completamente contenuto all’interno di un’altro grande e chiuso.
Supponiamo che il corpo esterno (detto 1) sia nero; chiamiamo S1 e S2
le superfici dei due corpi e T1 e T2 le rispettive temperature.
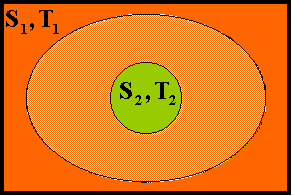
Fig. 3 – Un corpo contenuto dentro un altro
Si vede subito che ![]() e quindi
e quindi ![]() , cioè tutto il calore emesso dal corpo 2 viene assorbito dal
corpo 1. Si ha invece che solo parte del calore emesso dal corpo 1 viene
assorbito dal corpo 2, cioè
, cioè tutto il calore emesso dal corpo 2 viene assorbito dal
corpo 1. Si ha invece che solo parte del calore emesso dal corpo 1 viene
assorbito dal corpo 2, cioè ![]() .
.
Mettiamoci in condizioni isoterme, ossia ![]() ; la quantità di calore emessa deve essere pari a quella
ricevuta.
; la quantità di calore emessa deve essere pari a quella
ricevuta.
Sappiamo che la potenza emessa dalle superfici è
pari a
![]() (18)
(18)
![]() (19)
(19)
Per definizione di fattore di forma, inoltre, il
calore assorbito dal corpo 2 è pari a
![]() (20)
(20)
La potenza scambiata dal punto di vista del corpo
2 è
![]() (21)
(21)
ma se T1 = T2 allora trovo che il
fattore di forma è pari a
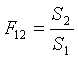 (22)
(22)
e questo valore è valido anche quando T1 e T2
non coincidono.
Sostituendo il valore del fattore di forma nella
(21) abbandonando le ipotesi restrittive precedenti trovo che la potenza
scmbiata da un corpo contenuto all’interno di un altro molto maggiore che può
essere considerato come un corpo nero è
![]() (23)
(23)
Se il corpo 1 non è più assimilabile ad un corpo
nero il sistema da risolvere si modifica in questo modo
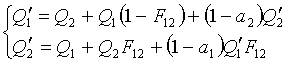 (24)
(24)
la cui soluzione inserita nella legge di Prevost
mi porta a
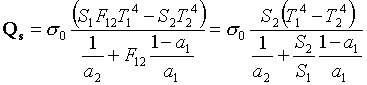 (25)
(25)
Questa ![]() vale per tutti i casi
in cui un corpo è completamente contenuto dentro un altro. Si vede infatti che
se
vale per tutti i casi
in cui un corpo è completamente contenuto dentro un altro. Si vede infatti che
se ![]() ossia se S1 fosse molto piccolo rispetto a S2
ritroveremmo la
ossia se S1 fosse molto piccolo rispetto a S2
ritroveremmo la ![]() che avevamo calcolato nel caso in cui il corpo 1 era nero.
che avevamo calcolato nel caso in cui il corpo 1 era nero.
Esercizio – Forno rotante per la cottura
del cemento
Dato un forno cilindrico rotante per la cottura del cemento, di lunghezza 5 m, diametro 1.5 m, con temperatura di parete 523 K, coefficiente di assorbimento 0.8, calcolare la potenza termica dispersa per irraggiamento dal forno sapendo che la temperatura ambiente è di 300K.
Dati
d = 1.5 m ![]() = 523K
= 523K
r = 5m ![]() = 300 K
= 300 K
a = 0,8
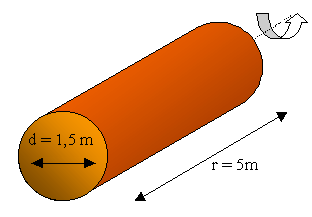
Fig. 4 – Forno rotante per la cottura del cemento
Soluzione
Consideriamo il forno piccolo rispetto al capannone industriale, che verrà quindi trattato come un corpo nero.
![]() (26)
(26)
che è un valore molto alto. Si può provare ad abbassarlo inserendo intorno
al tubo una schermatura fissa di lamiera di diametro ![]() e
e ![]() .
.

Fig. 5 – Forno rotante con schermatura
Per calcolare la potenza emessa dal forno mi manca
la temperatura della schermatura. Posso però considerare lo scambio tra il
forno e l’esterno come somma di due scambi, il primo tra il forno e la
schermatura e il secondo tra la schermatura e l’esterno. Ricavo quindi ![]() in due modi diversi.
in due modi diversi.
·
Tra forno e
schermatura
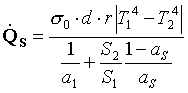 (27)
(27)
·
Tra schermatura ed
esterno
![]() (28)
(28)
Eguaglio le due espressioni ed ottengo una
equazione del 4° grado, non molto facile da risolvere analiticamente.
Procedendo per tentativi si giunge al risultato di ![]() .
.
Possiamo quindi calcolare la potenza in uscita che
risulta
![]()
![]() (29)
(29)
che è meno di un terzo di quella calcolata senza
schermatura.
L’introduzione di questa schermatura, inoltre, non
comporta errori significativi anche in presenza di fenomeni di convezione.
Osservazione
Visto che le relazioni appena osservate sono
funzioni di ![]() , per poterle utilizzare insieme ad altre resistenze termiche
spesso si costruisce una resistenza equivalente del tipo
, per poterle utilizzare insieme ad altre resistenze termiche
spesso si costruisce una resistenza equivalente del tipo
![]() (30)
(30)
con 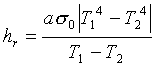 (31)
(31)
Questo metodo non è preciso, visto che la
resistenza così costruita non è lineare, ma siccome la potenza scambiata per
irraggiamento è bassa in presenza di fenomeni convettivi o conduttivi, questo
tipo di artificio comporta un errore generalmente non superiore al 1%.
Esercizio – Tubo con isolante
E’ dato un tubo di acciaio lungo un metro, di cui
sono noti raggio interno ed esterno ![]() e conducibilità termica
e conducibilità termica ![]() , ricoperto da uno strato di isolante di cui conosciamo il
raggio
, ricoperto da uno strato di isolante di cui conosciamo il
raggio ![]() , il coefficiente di assorbimento a e la conducibilità
termica
, il coefficiente di assorbimento a e la conducibilità
termica ![]() . All’interno del tubo scorre acqua di cui conosciamo la
temperatura
. All’interno del tubo scorre acqua di cui conosciamo la
temperatura ![]() , la velocità v e il grado igrometrico
, la velocità v e il grado igrometrico![]() .
.
E’ nota inoltre la temperatura dell’ambiente.
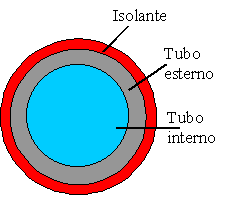
Fig. 6 – Tubo in acciaio con isolante
Calcolare se il raggio dell’isolante è sufficiente
ad evitare la formazione di rugiada sulla superficie del tubo.
Dati
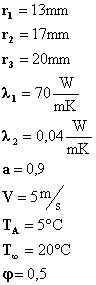
Soluzione
Sul diagramma psicrometrico troviamo che ad un
grado di 0,5 alla temperatura esterna di 20°C corrisponde una temperatura di
rugiada di 9,8°C. Per sicurezza verificheremo che la temperatura di parete
esterna sia ![]() .
.
Il circuito equivalente per questo sistema è
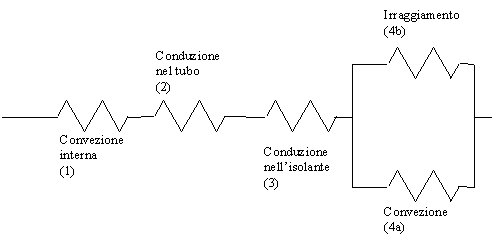
Fig. 7 – circuito equivalente
Calcoliamo uno ad uno il valore delle resistenze
termiche
(1)
Troviamo il numero
di Reynolds
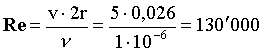 (32)
(32)
Il numero di Nusselt, sapendo che ![]() per l’acqua a 5°C, diventa
per l’acqua a 5°C, diventa
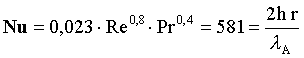 (33)
(33)
Tra i valori tabellati troviamo la conducibilità
dell’acqua ![]() , che ci permette di ricavare il coefficiente di convezione h
, che ci permette di ricavare il coefficiente di convezione h
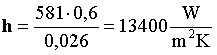 (34)
(34)
A questo punto possiamo calcolare la prima
resistenza
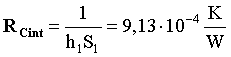 (35)
(35)
(2)
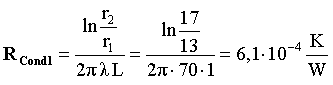 (36)
(36)
(3)
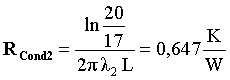 (36)
(36)
Rispetto a ![]() possono essere
considerate trascurabili.
possono essere
considerate trascurabili.
(4)
E` presente solo
convezione naturale. Calcoliamo il numero di Grasshof
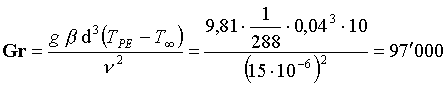 (37)
(37)
da cui ricaviamo che il moto è laminare. Con i
valori tabellati di a, b e C troviamo che il numero di Nusselt è pari a
![]() (38)
(38)
da cui ricavo il coefficiente di convezione
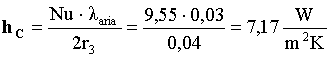 (39)
(39)
Calcoliamo ora il coefficiente di irraggiamento,
che sommeremo al coefficiente di convezione, usando la formula semplificata
(31) descritta sopra
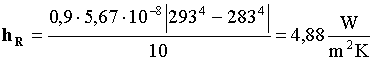 (40)
(40)
Il coefficiente complessivo è la somma dei due
cioè
![]() (41)
(41)
Il valore della resistenza equivalente è quindi
pari a
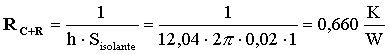 (42)
(42)
Ora ho tutto quello che mi serve; ricostruisco il
mio circuito semplificato che trovo essere di questa forma
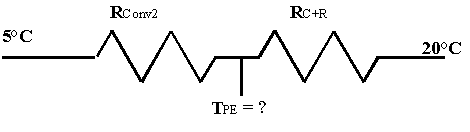
Fig. 8 – circuito semplificato
Siccome ![]() e
e ![]() sono quasi uguali, si può dire che la temperatura tra le due
resitenze sarà all’incirca la media tra le temperature agli estremi del
circuito, ossia che la temperatura di parete varrà
sono quasi uguali, si può dire che la temperatura tra le due
resitenze sarà all’incirca la media tra le temperature agli estremi del
circuito, ossia che la temperatura di parete varrà
![]() (43)
(43)
che, essendo un valore superiore a 10°C, mi
assicura che l’isolante è sufficiente per evitare la formazione di rugiada.
Appendice
Tabella diametro interno delle tubazioni
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tabella diametro
esterno delle tubazioni
Pollici
|
DiametroNominale
|
Acciaio
|
PE - PVC
|
Ghisa
|
Fibrocemento
|
||||
|
6
- B |
10
- C |
12,5
- D |
15
- E |
17,5
- F |
|||||
|
1/8" |
- |
10.3 |
- |
- |
- |
- |
- |
- |
- |
|
1/4" |
- |
13.7 |
- |
- |
- |
- |
- |
- |
- |
|
3/8" |
10 |
17.2 |
16 |
- |
- |
- |
- |
- |
- |
|
1/2" |
15 |
21.3 |
20 |
- |
- |
- |
- |
- |
- |
|
3/4" |
20 |
26.9 |
25 |
- |
- |
- |
- |
- |
- |
|
1" |
25 |
33.7 |
32 |
- |
- |
- |
- |
- |
- |
|
1" 1/4 |
32 |
42.4 |
40 |
- |
- |
- |
- |
- |
- |
|
1" 1/2 |
40 |
48.3 |
50 |
- |
- |
- |
- |
- |
- |
|
2" |
50 |
60.3 |
63 |
- |
- |
- |
- |
- |
- |
|
2" 1/2 |
60 - 65 |
76.1 |
75 |
77 |
78 |
78 |
78 |
78 |
78 |
|
3" |
80 |
88.9 |
90 - 110 |
98 |
98 |
98 |
102 |
106 |
110 |
|
4" |
100 |
114.3 |
110 - 125 |
118 |
118 |
120 |
126 |
132 |
136 |
|
5" |
125 |
139.7 |
125 - 140 |
144 |
143 |
147 |
153 |
159 |
165 |
|
6" |
150 |
168.3 |
160 - 180 |
170 |
168 |
174 |
182 |
190 |
196 |
|
7" |
175 |
- |
- |
197 |
195 |
201 |
211 |
219 |
227 |
|
8" |
200 |
219.1 |
200 - 225 |
222 |
222 |
234 |
244 |
252 |
262 |
|
9" |
225 |
- |
- |
248 |
249 |
253 |
269 |
281 |
293 |
|
10" |
250 |
273 |
250 - 280 |
274 |
276 |
286 |
296 |
306 |
318 |
|
12" |
300 |
323.8 |
315-355 |
326 |
330 |
344 |
354 |
368 |
380 |
|
14" |
350 |
355.6 |
355-400 |
378 |
384 |
400 |
414 |
428 |
442 |
|
16" |
400 |
406.4 |
400-450 |
429 |
438 |
456 |
472 |
490 |
504 |
|
18" |
450 |
457.2 |
450-500 |
480 |
492 |
512 |
534 |
550 |
566 |
|
20" |
500 |
508 |
500-560 |
532 |
546 |
570 |
592 |
612 |
626 |
|
24" |
600 |
609.6 |
630 |
635 |
- |
680 |
696 |
720 |
- |
Tutte
le misure a parte la prima colonna (pollici) sono espresse in mm.
Tabella Spessori isolanti minimi delle condotte
|
Conduttività termica utile (W/m °C) |
Spessore dell'isolante (mm) |
||
|
Condotte tipo "A" |
Condotte tipo "B" |
Condotte tipo "C" |
|
|
0.030 |
19 |
9.5 |
5.7 |
|
0.032 |
21 |
10.5 |
6.3 |
|
0.034 |
23 |
11.5 |
6.9 |
|
0.036 |
25 |
12.5 |
7.5 |
|
0.038 |
28 |
14.0 |
8.4 |
|
0.040 |
30 |
15.0 |
9.0 |
|
0.042 |
32 |
16.0 |
9.6 |
|
0.044 |
35 |
17.5 |
10.5 |
|
0.046 |
38 |
19.0 |
11.4 |
|
0.048 |
41 |
20.5 |
12.3 |
|
0.050 |
44 |
22.0 |
13.2 |
Note:
Le condotte tipo A
corrono in ambienti non riscaldati.
Le condotte tipo B
corrono all’interno dell’isolamento termico dell’edificio verso l’interno del
fabbricato.
Le condotte tipo C
corrono all’interno degli edifici e in locali riscaldati.
I dati riportati nella
tabella seguente sono forniti a titolo indicativo per la progettazione di
massima. I valori utili da adottare nella progettazione
esecutiva di dettaglio devono essere sempre desunti dal valore dichiarato dal
produttore, se certificato. I dati sono riferiti alla temperatura media di 40°C
e tengono conto dell’influenza della posa, delle tolleranze di spessore, delle
tolleranze di produzione, del comportamento nel tempo, della stabilita
dimensionale, ecc., in senso generale.
|
Tipo di materiale |
Configurazione |
Densità (Kg/m³) |
l a 40°C (W/mK) |
|
Lana di vetro |
feltri |
19 |
0.050 |
|
22 |
0.046 |
||
|
55 |
0.041 |
||
|
pannelli |
22 |
0.046 |
|
|
60 |
0.040 |
||
|
coppelle |
60 |
0.039 |
|
|
Lana di roccia |
feltri |
80 |
0.047 |
|
120 |
0.044 |
||
|
pannelli |
60 |
0.044 |
|
|
120 |
0.041 |
||
|
coppelle |
100 |
0.041 |
|
|
Polietilene (PEF) estruso in continuo, non reticolato, in tubi |
tubi |
30 |
0.045 |
|
Polietilene (PEF) espanso in continuo reticolato termosaldato |
|
30 |
0.045 |
|
Polietilene (PEF) espanso in continuo in lastre reticolato |
lastre |
30 |
0.045 |
|
Poliuretano espanso Pur/Pir in coppelle
|
coppelle
|
15 |
0.040 |
|
20 |
0.039 |
||
|
40 |
0.038 |
||
|
Poliuretano espanso Pur/Pir in flessibile
|
coppelle
|
15 |
0.040 |
|
30 |
0.039 |
||
|
Poliuretano espanso Pur/Pir espanso in situ |
|
30 |
0.045 |
|
Elastomeri espansi (FEF) estrusi in continuo
|
|
55 |
0.040 |
|
70 |
0.040 |
||
|
Resine fenoliche (FF) espanse |
coppelle |
30 |
0.038 |
|
Polistirene (PSE) espanso |
coppelle |
20 |
0.045 |
|
Polistirene estruso (PER) rigido |
coppelle |
30 |
0.040 |
Tab. 2.11 - Conduttività termiche
indicative di riferimento di alcuni materiali isolanti tratte da UNI 10376