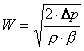Diagramma di Moody

Il diagramma di Moody (fig.1) serve a determinare il fattore di attrito che viene indicato con la lettera x minuscola, questo coefficiente è indispensabile per il calcolo delle perdite di carico distribuite, è funzione di due variabili proprie di ogni moto in un circuito idraulico:

dove Re è il numero di Reynolds, numero puro indicativo del tipo di moto che si verifica all’interno di un condotto per valori di Re inferiori a 2100 il moto è puramente laminare, definito da:

dove D è il diametro del tubo, W è la velocità media del fluido, r la sua densità e m la sua viscosità.

Al di sopra di 4000 Re il moto è turbolento vi è una zona di transizione in cui è facile l’instaurarsi di un moto misto tra 2100¸4000 Re; il rapporto e/D è la scabrezza relativa, e è l’asperità media del condotto e D è il diametro.

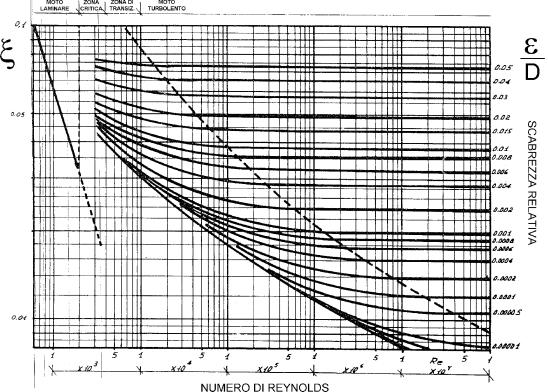
Figura 1. Diagramma di Moody

Sul diagramma appare sull’ascissa il numero di Reynolds che viene espresso in scala logaritmica divisa in decadi, sull’ordinata di destra leggiamo il fattore di attrito fra tutte le linee e necessario scegliere quella corrispondente al valore di scabrezza relativa del condotto in esame indicato sulla destra.

La retta sulla sinistra indica il valore di x nel caso di moto strettamente laminare,

nella zona al di sopra della linea tratteggiata il moto è fortemente turbolento le linee sono orizzontali e x è indipendente da Re, è funzione solo della scabrezza relativa, a sinistra della linea tratteggiata è ancora turbolento ma x dipende da entrambi i parametri; la curva più bassa è invece detta del tubo liscio.

La zona centrale detta di transizione comprende delle regioni metastabili infatti procedendo dal basso in particolari condizioni e molto lentamente è possibile osservare moto laminare per valori di Re di circa 3000, stati di precario equilibrio in cui la minima perturbazione causa il passaggio ad un moto turbolento; una buona progettazione di un condotto idraulico non deve prevedere il funzionamento in regime di transizione perché, ciò può causare: errori nel calcolo delle perdite e fenomeni di tipo oscillatorio molto dannosi, causa di vibrazioni dell’impianto e di inopportuni rumori; basti pensare all’apertura di un rubinetto quando in un determinato punto le tubazioni entrano in vibrazione e si genera una sorta di fischio.

Le perdite in regime laminare sono molto piccole rispetto al regime turbolento, è quindi di fondamentale importanza usare le formule opportune in base alla regione in cui ci si trova, perché usare le formule per il regime turbolento nella regione laminare ci porta a grossolani errori:

Nel caso di moto laminari in un tubo rettilineo con sezione costante perfettamente liscio (tubo liscio) le perdite sono:

in cui :

è il coefficiente di attrito; nel caso ci trovassimo fuori dalle condizioni imposte bisognerà calcolare x con il diagramma di Moody.

Il moto laminare comunque trova applicazione raramente, con fluidi come olio, vaselina, burro e glicerina, tutte sostanze molto viscose, acqua e aria sono poco viscose e vanno sempre a finire i regime turbolento.

PERDITE LOCALIZZATE

Finora abbiamo parlato di perdite distribuite, ma in un condotto, la causa di perdite di carico possono essere anche accidentalità proprie del condotto, ad esempio curve, raccordi, valvole ecc. che il fluido si trova a dover superare.

Riportiamo di seguito una tabella riassuntiva di tali accidentalità con i relativi coefficienti di perdita localizzata:

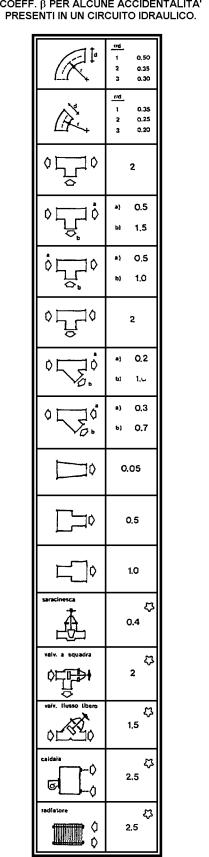
Figura 2. Tabella Accidentalità

Il problema ora è di capire come possono questi ostacoli influenzare il moto e causare una perdita di carico, sicuramente ci sarà una proporzionalità diretta fra l’energia cinetica del fluido e le perdite attraverso un coefficiente opportuno inoltre non vi sarà più dipendenza dalla lunghezza del condotto propria del concetto di perdita distribuita, la relazione infatti è:

dove b chiamato anch’esso coefficiente d’attrito, dipende dalla particolare geometria dell’oggetto ed è tabulato (fig.2), e la velocità va misurata a monte dell’accidentalità.

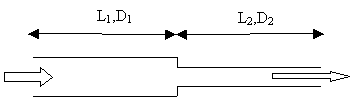
Vediamo ora un esempio di come un brusco restringimento del condotto causa una perdita di carico, supponiamo di osservare il profilo del tubo:

Figure 3. Schematizzazione di una strozzatura

La tabella ci dice che un’accidentalità di questo tipo ha un coefficiente di attrito b=0,5 quindi considerando tutto il tratto in figura avremo perdite di carico distribuite dovute al tubo stesso e la perdita localizzata a causa della strozzatura.

Partiamo col dire che la portata M₁ in entrata sarà uguale alla M₂ in uscita quindi avremo:

Questa uguaglianza è detta equazione di continuità, se consideriamo densità costante in tutto il tratto l’equazione si semplifica e si ottiene:

quindi se diminuisce la sezione aumenta necessariamente la velocità, inoltre essendo i tratti di differente diametro bisogna trattarli separati e si avrà:

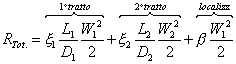
inoltre la differenza di velocità comporta il cambiamento del numero di Reynolds e di conseguenza del coefficiente di attrito x, sarà quindi necessario avvalersi due volte del diagramma di Moody.

ANALOGIE TRA CIRCUITI IDRAULICI E ELETTRICI

Se consideriamo l’equazione di Bernoulli:

ed in particolare andiamo ad analizzare l’espressione dell’ultimo termine del primo membro:

che abbiamo definito come resistenza idraulica, ci accorgiamo come questo termine sia pressoché equivalente alla resistenza elettrica definita come:

ma le analogie non si fermano qui, infatti, se andiamo a considerare i vari elementi che si possono incontrare in un circuito idraulico ed elettrico si possono riscontrare notevoli somiglianze, com’è possibile vedere nel seguente specchietto:

Elementi idraulici	Elementi elettrici
Caduta di pressione (DP)	Caduta di tensione (DV)
Portata ()	Corrente (I)
Resistenza idraulica (R)	Resistenza elettrica (R)
Pompa	Generatore di tensione
Serbatoio	Condensatore
Inerzia del liquido	Induttanza

Figura 4. Analogie tra circuiti elettrici e idraulici.

Nasce allora l’idea di paragonare una conduttura idraulica con un circuito elettrico puramente resistivo dove ogni perdita di carico e assimilabile ad una

resistenza elettrica:

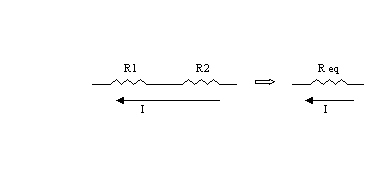
Figura 5.Resistenze elettriche in serie e resistenza equivalente

Come nei circuiti elettrici una serie di resistenze può essere sostituita da una resistenza equivalente anche nei circuiti idraulici è possibile calcolare una resistenza idraulica equivalente.

Tuttavia, proprio la resistenza, che ad una prima approssimazione può sembrare equivalente in entrambi i circuiti, in realtà nasconde una grande differenza; infatti, mentre la resistenza dei circuiti elettrici può essere facilmente rappresentata mediante la legge di Ohm, che è evidentemente una relazione lineare che lega la caduta di tensione con la corrente, nei circuiti idraulici la resistenza idraulica è descritta da:

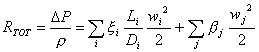
inoltre considerando che

è evidente come

valere a dire che la resistenza, nei circuiti idraulici, dipende dal quadrato della portata, e non linearmente come l’omologo nei circuiti elettrici.

Inoltre nei circuiti elettrici è necessaria la presenza di un generatore, si può pensare per esempio ad una pila che eroghi 1,5 V a vuoto, ogni pila ha una corrente massima I_max detta corrente di cortocircuito pari alla corrente ottenuta azzerando la differenza di potenziale, il cui grafico risulta:

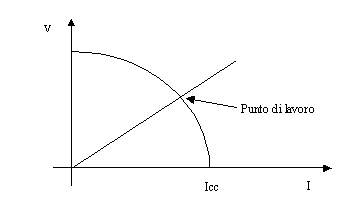
Figure 6. Grafico di funzionamento generatore elettrico

ma, basti pensare ad una pompa idraulica, l’analogia è pressoché totale, infatti, il suo funzionamento è analogo a quello di un generatore di tensione, come descritto in figura:

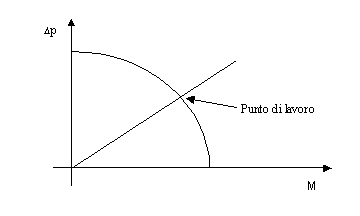
Figura 7. Grafico prevalenza/portata di una pompa

dove Dp rappresentata la prevalenza, valere a dire la differenza di pressione ai capi della pompa, in funzione di della portata, rispettivamente al posto della tensione e della corrente, come nel comportamento ideale dei generatori elettrici la linea dovrebbe essere orizzontale, ma a causa della viscosità del liquido, che traduce una sorta di resistenza interna, é in realtà decrescente.

Sul grafico è facile individuare il punto in cui la curva intercetta l’asse della ascisse, dove cioè abbiamo massima portata ma prevalenza nulla ,oltre il quale, quindi, la pompa gira a vuoto, come per altro avviene nei generatori di tensione nel punto di cortocircuito.

Nel caso trattato, il carico applicato alla pompa era di tipo lineare, questo nei circuiti idraulici è assimilabile al caso di regime laminare vista la dipendenza del moto principalmente dalla sua velocità, nel moto turbolento il carico non è più lineare è il parallelismo idro-elettrico è inaccettabile vista l’imprevedibilità di un moto perturbato.

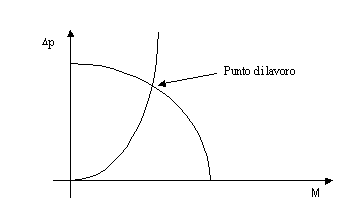
Figura 8. Grafico ipotetico di pompa in regime laminare

LUNGHEZZA EQUIVALENTE

Le accidentalità nei calcoli possono essere trattate in altro modo da come abbiamo visto, è possibile grazie alla teoria della lunghezza equivalente, sostituire la perdita di carico localizzata dovuta ad esempio ad una valvola o ad un imbuto, con la corrispondente perdita di carico distribuita come se il condotto fosse più lungo, tanto quanto necessario per avere una perdita uguale a quella dovuta all’accidentalità.

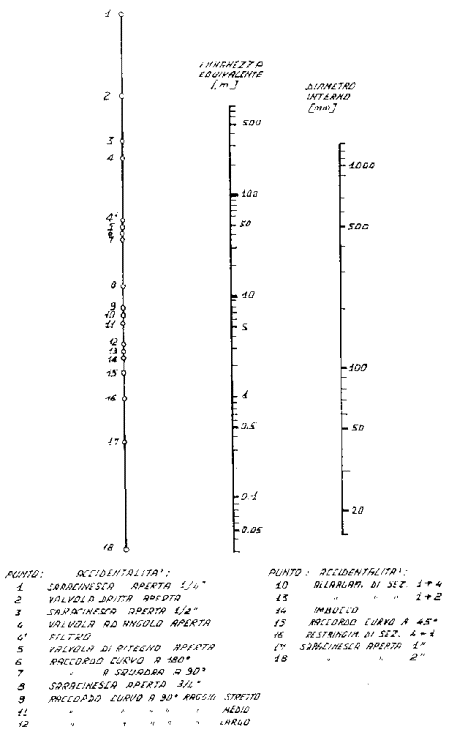
Figura 9. Nomogramma lunghezza equivalente

Supponiamo che in un condotto sia presente un diaframma con b=5 il calcolo sarebbe:

il che ci suggerisce di sostituire a b un espressione tipo perdita distribuita:

espressione dove L_EQ. È la lunghezza equivalente cercata.

Tale valore è proprio di ogni accidentalità ma varia al variare del diametro del condotto per cui dobbiamo ricorrere ad un nomogramma (fig. 9) per la sua determinazione.

Nella scala di destra si sceglie il diametro del condotto, in quella di sinistra un numero che corrisponde nella legenda ad una precisa accidentalità, si traccia una retta e il valore che si legge sulla scala centrale è quello cercato.

TUBI NON TONDI E DIAMETRO EQUIVALENTE

Finora abbiamo fatto ipotesi e usato leggi nel caso generico di un condotto a sezione circolare ma nelle applicazioni reale e molto comune trovare condotti con sezioni particolari es. triangolari, quadrate, rettangolari ecc. ecc.

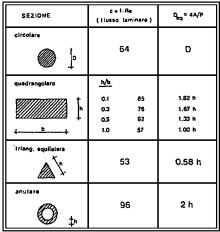
Figura 10. Tabella diametro equivalente tubi non tondi

Ci viene in aiuto la tabella in figura che riporta per alcuni tubi di sezione particolare il valore del diametro equivalenti da usare nei calcoli di modo da poter usare le formule sinora viste; da notare il valore del tubo quadrato il cui diametro equivalente è semplicemente il lato.

Questo è facilmente dimostrabile applicando la formula per tale calcolo infatti il diametro equivalente si ottiene:

nel caso di sezione quadrata sarà:

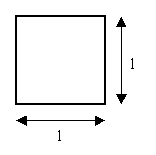
per una sezione triangolare equilatera:

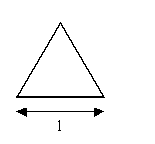
per una sezione a corona:

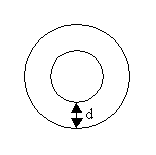
APPROFONDIMENTO SULLE ACCIDENTALITA’

In commercio si trova materiale idraulico di molti tipi differenti per ogni singolo componente, a partire dal prezzo fino a materiali e caratteristiche tecniche particolari, fra i materiali più diffusi ricordiamo ghisa, rame, acciaio e materiali plastici polipropilici.

Di seguito riportiamo esempi grafici di alcune accidentalità presenti nella legenda del nomogramma in figura 9.

· Curve a bicchiere

Angolo 90° Angolo 45° Angolo 22°

· Curve a flange

Angolo 90° Angolo 45° Angolo 22°

· Manicotto rettilineo a bicchiere

· Imbocco a flangia

· Riduzione a flange

· Raccordo a tre vie a flange

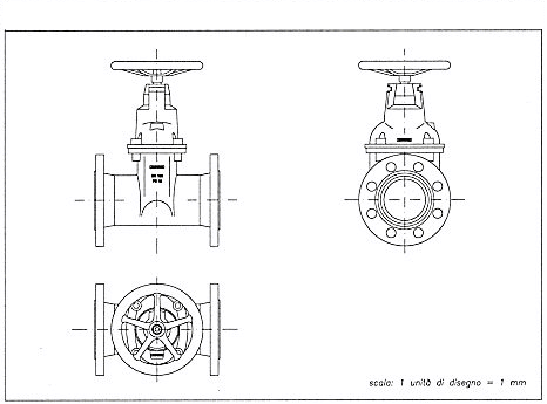
· Saracinesca a cuneo gommato

· Alcune immagini

Curva zincata femmina/femmina

Curva zincata femmina/maschio

Manicotto zincato femmina/femmina

Nota: Immagini e disegni www.oppo.it

STRUMENTI DI MISURA PER FLUIDODINAMICA

METODO DELLA PESATA

E’ il metodo più semplice e immediato che permette di determinare la portata di un fluido, l’apparecchiatura è costituita da un recipiente graduato in cui finisce il fluido di cui si vuole misurare la velocità, che esce dal condotto in esame.

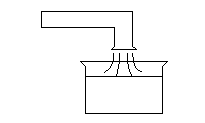
Figura 11. Metodo della pesata

Conoscendo la quantità di liquido che riempie il recipiente in un dato periodo di tempo siamo in grado di calcolarci la portata in massa tramite la formula elementare :

Questo metodo, ha grossi limiti dal punto di vista della precisione, infatti non è per niente facile sincronizzare l’inizio del tempo della misura con l’arrivo del liquido nel recipiente; infatti si capisce che al tempo iniziale t=0 a cui corrisponde l’apertura della valvola il flusso dell’acqua non arriverà subito a regime, ma ci sarà un transitorio di tempo in cui il flusso del liquido uscirà più piano.

Tuttavia il tempo può essere rilevato con cronometri al centesimo di secondo e la quantità dell’acqua può essere effettuata sull’ordine del milligrammo, il che fa si che tale metodo venga utilizzato per tarare altri strumenti di misura, naturalmente il fluido deve essere o liquido oppure solubile in acqua.

TUBO DI PITOT

Figura 12. Alcuni tubi di Pitot in commercio

E’ un metodo per la misura di velocità locali, si basa sulle considerazioni sperimentali effettuate da H.Pitot (1732) che , immergendo in una corrente liquida un tubo, piegato ad angolo retto, aperto da ambedue le estremità, una delle quali rivolta controcorrente, il liquido sale in esso al di sopra del livello statico di una altezza proporzionale all’altezza cinetica:

ove W è la velocità del fluido nel punto considerato e g è la accelerazione di gravità.

Successivamente H. Darcy unì due tubi uno rivolto contro corrente e l’ altro in senso opposto; il dislivello tra i due menischi era ancora proporzionale all’altezza cinetica quindi la velocità risultava dalla a formula:

ove con (h₁ –h₂₎ si è indicato il dislivello tra i due menischi e con K un coefficiente di velocità che dipende dalla forma dell’estremità, dal tipo di fluido e dalle condizioni di moto; i tubi di Pitot che sono attualmente in uso sono: il tipo Prandtl, che ha l’estremità semi sferica, ed il tipo Brabbè, che ha l’estremità a tronco di cono.

Viene utilizzato molto per la misura di velocità elevate perché poco adatto alle basse velocità, ad esempio a bordo di aeroplani o in galleria del vento e non nei canali di ventilazione.

Entrambi i tipi sono formati da due tubi coassiali. Il tubo esterno presenta dei fori paralleli alla direzione della velocità (presa statica). Essi sono posti in modo tale che la pressione all’interno è pari alla pressione corrispondente al livello statico. Il tubo interno ha l’estremità controcorrente (presa dinamica).

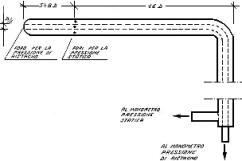
Figura 13 : Tubo di Pitot , sezione laterale.

Generalmente è di acciaio inox, può essere di diverse misure, si va da lunghezze di qualche centimetro e diametro di qualche millimetro a lunghezze di un metro e diametro di qualche centimetro.

La parte perpendicolare al terreno è detta gambo, mentre quella orizzontale al terreno è detta testa e può essere lunga una ventina di diametri.

Lo strumento va puntato nella direzione opposta al verso del fluido di cui si vuole misurare la velocità. Come si nota in figura il tubo è chiuso nella parte finale del gambo da un manometro; il fluido entra dalla testa del tubo, ma una volta riempiti gambo e testa è come se lo strumento fosse chiuso nella parte frontale, e quindi il fluido si vede costretto a girare attorno alla punta della testa. Nella parte iniziale della testa si ha evidentemente velocità nulla nel punto di ristagno e di conseguenza un massimo di pressione.

Ad una distanza dalla punta della testa di circa 5-8 diametri, il fluido ha riacquistato la sua velocità, e qui grazie ai fori laterali viene rilevata la pressione statica.

Vediamo ora di risalire alla formula che mi permette di calcolare la velocità W del fluido partendo dall’equazione di Bernoulli:

Innanzitutto individuiamo 2 sezioni, rispettivamente una all’ingresso del tubo e una all’altezza dei fori della pressione statica; alcuni termini dell’equazione possono essere trascurati: le perdite di carico R perché il tubo è costruito a bassa resistenza aerodinamica in modo che possano essere trascurate, il termine legato alla differenza di livello, in virtù del fatto che la posizione dei fori per la presa statica e l’asse del tubo stesso sono alla stessa quota, la componente del lavoro –l e poi la velocità W₁ nella sezione 1 in quanto l’ingresso è un punto di ristagno e quindi W₁ = 0.

Quindi con tali semplificazioni l’equazione diventa :

da cui :

evidente è la dipendenza della velocità dalla differenza di pressione, quindi è necessario applicare dei manometri all’estremità aperte della coda o ancor meglio una manometro differenziale.

Micromanometro a tubo inclinato

E’ un manometro a colonna di liquido impiegato per misurare differenze di pressione molto piccole. Esso è formato da un serbatoio, sul quale grava la pressione P in esame e in cui pesca un tubo di vetro molto sottile, con un’angolazione nota α e comunicante con un recipiente a pressione prefissata o lasciato alla pressione atmosferica.

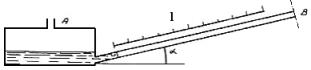
Figura 14: Manometro a tubo inclinato, sezione laterale.

Lungo il tubo si trova una scala graduata dove si andrà a leggere un valore di pressione proporzionale a P, sarà necessario moltiplicare il valore letto per senα per ottenere il valore cercato.

Manometri differenziali

Il principio alla base di questo tipo di strumenti è misurare la differenza di pressione tramite un effetto che tale differenza apporta alla proprietà di un corpo,

Un tubo di vetro a U con del mercurio le cui due estremità sono sottoposte alle pressioni in esame è l’esempio più elementare ma non precisissimo, il manometro a membrana sfrutta la sensibile elasticità di una membrana che sottoposta alla differenza di pressione si sposta muovendo un indicatore su una scala.

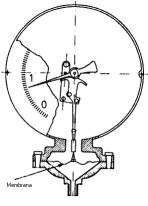
Figura 15: Manometro a membrana, sezione frontale, la membrana

è collegata con opportune leve all’indicatore

I manometri a membrana sono utilizzati per misurare pressioni statiche molto basse inferiori a 50 bar.

La tecnologia a messo a punto questi dispositivi mettendo in commercio apparecchi elettronici sofisticati che però sfruttano sempre i soliti principi di base.

Figura 16. Manometro differenziale digitale

Nell’effettuare una misurazione di velocità locale, con il tubo di Pitot o con altri strumenti simili è necessario operare in modo statistico, cioè misurare il valore della velocità più volte, in punti del condotto differenti, in quanto all’interno di un tubo il flusso, anche in regime laminare, non è perfettamente uniforme.

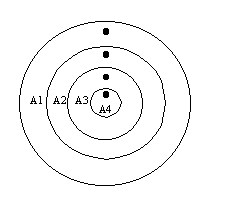
Figura 17. Sezione condotto

Supponiamo di rilevare la velocità in un condotto a sezione circolare, inserendo il tubo di Pitot attraverso un foro di ispezione, suddividiamolo idealmente in corone concentriche, effettuiamo quattro misurazioni o più a seconda del raggio del condotto, in corrispondenza delle ideali corone, in corrispondenza ad esempio dei puntini spostandosi lungo un raggio.

Se con A₁, A₂, ecc. ecc. chiamo le aree delle corono circolari, allora la velocità media locale W finale sarà:

Nonostante tali espedienti matematici questo strumento non è particolarmente adatto alle basse velocità quindi ai regimi laminari, perché all’interno del condotto in regime laminare, le velocità locali dipendono fortemente dal raggio, secondo la parabola di Poiseville, infatti la velocità massima può essere anche due volte la velocità media, invece ad alte velocità in regime turbolento la velocità massima raggiunge al più 1,1 volte la velocità media.

VENTOLINE

Per velocità molto piccole si usano le ventoline o anemometri a pale, costituite da una ventola che viene esposta al flusso, il quale mette in movimento la ventola che fornisce impulsi elettrici attraverso un magnete posto su una pala e un sensore sul supporto, generando un’onda che elaborata matematicamente fornisce il valore della velocità.

E’ tipico il loro utilizzo negli impianti aerazione perché avendo una superficie abbastanza elevata possono mediare automaticamente l’effetto del flusso disuniforme.

Figura18. Ventoline portatili elettroniche

Venturimetro

Strumento di misura della portata transitante in una condotta, detto anche contatore di Venturi.

Come si può osservare in figura ,lo strumento è costituito da tre manometri situati nei tre punti indicati con 1,2,3 e da un tubo che prima subisce una brusca riduzione di sezione e poi un molto più graduale allargamento fino a tornare come all’inizio.

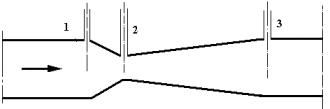
Figura 19. Venturimetro , vista laterale

Il manometro 3 non è di utilità diretta nella misura della velocità, in quanto serve per controllare che la pressione sia ritornata la stessa che si ha in 1, di solito viene recuperata circa il 90% della potenza che c’è in uno, il tubo di Venturi infatti è uno strumento che non deve dar luogo a perdite di carico lungo il circuito idraulico, per questo spesso viene fatto in modo di poterlo inserire in un circuito solo al momento della misura con opportune valvole, oppure installato fisso ma in modo da poterlo escludere dal circuito can chiuse le quali cadute saranno considerate nei calcoli.

In questo caso viene calcolata la velocità media, mettendola in relazione con la pressione, tramite l'equazione di continuità; tale equazione viene scritta per il tubo di flusso che ha come sezione iniziale e finale le sezioni 1 e 2, e come profilo laterale lo stesso tubo.

Dall'equazione di Bernoulli, supposto il condotto orizzontale ed il fluido incomprimibile, si ha:

le perdite di carico non si considerano perché nulle per un restringimento di sezione; in questo caso compaiono due velocità, si tratta quindi di esprimere una velocità in funzione dell'altra, tramite una relazione ottenuta dall'equazione di conservazione della massa.

da cui:

dove A₁ e A₂ sono le aree delle superfici delle sezioni di entrata e di uscita; la densità r viene supposta costante ipotizzata l’incomprimibilità del fluido, quindi è possibile semplificarla, inoltre trattandosi di sezioni circolari, la superficie è proporzionale al quadrato dei raggi, quindi:

da cui si ricava la velocità W₂ in funzione di W₁:

si sostituisce ora l'espressione della velocità W₂ nell'equazione di Bernoulli:

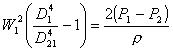
In questo modo si ottiene l'espressione della velocità W₁:

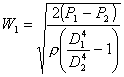
Naturale vista l’asimmetria del condotto di Venturi l’unidirezionalità di funzionamento, da notale la relazione finale molto simile a quella ottenuta con il tubo di Pitot.

Diaframmi e boccagli

Tutti e due questi strumenti sfruttano la perdita di carico concentrata dovuta ad un volontario inserimento di una sorta di barriera ottenuta per mezzo di un restringimento e successivo allargamento della sezione del tubo; lasciando con due fori la possibilità di misurare la pressione prima e dopo l’ostacolo.

Figura 20. Diaframma, sezione condotto

Applicando la forma operativa dell’equazione di Bernoulli a questo semplice sistema risulta:

ove è possibile ottenere la misura di Dp per mezzo di un manometro differenziale, si ottiene :

ove r è la densità del fluido e b, coefficiente di perdita concentrata proprio dello strumento data dal costruttore.

Vi sono vantaggi nell’utilizzare tali sistemi, ad esempio sono facilmente intercambiabili e con un intervallo di velocità W misurabili più ampio, grazie a diversi valori di b che può assumere lo strumento d’altro canto si perde in precisione viste le probabili asimmetrie di installazione e produzione, le perdite di carico sono maggiori e hanno l’enorme svantaggio di interferire col moto del fluido; come ad esempio nel campo di applicazioni alimentari in cui vi può essere l’accumulo di residui alimentari lungo il condotto.

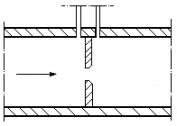
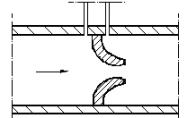
Figura 21. Boccaglio , sezione condotto.

ROTTAMETRO O FLUSSIMETRO

Appartiene alla categoria dei flussometri, strumenti idonei alla misura di portate piccole o medie. E’ sono costituiti da un tubo di vetro conico entro cui si trova un galleggiante, che può avere sezione conica, come è illustrato in figura, o sferica.

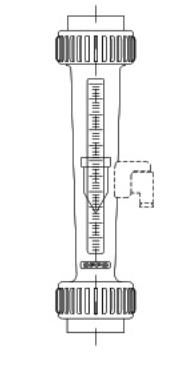
Figura 22. Rottametro o flussimetro.

Deve essere installato verticalmente con l’entrata in basso e l’uscita in alto. La misura si basa sul fatto che il fluido, investe il galleggiante e l’oltrepassa, subendo una perdita di pressione localizzata, dovuta al restringimento della sezione di passaggio. Si ottiene quindi un equilibrio tra la spinta dovuta alla differenza di pressione a monte e a valle del galleggiante ed il peso del galleggiante stesso.

Questo equilibrio è costante, finchè il flusso non aumenta, si ha un incremento della caduta di pressione che provoca il sollevamento del galleggiante fino ad nuovo equilibrio. Si stabilisce allora una relazione tra la portata e la posizione del galleggiante; la posizione viene letta su una scala graduata incisa sul tubo di vetro o affiancata ad esso.

I rottametri richiedono una taratura rispetto a condizioni di pressione, di temperatura e tipo di fluido perché si basano sulla viscosità, proprietà molto sensibile alle condizioni elencate.

ANEMOMETRO LASER-DOPPLER

Questo strumento basa il suo funzionamento sul fenomeno sul dell’interferenza fra raggi luminosi; è dimostrato che quando due raggi di luce coerenti si incrociano, si genera una zona detta delle frange di interferenza, in cui tali frange sono visibili. L’inserimento di un fotomoltiplicatore, ossia uno strumento in grado di rilevare fenomeni luminosi, ottengo un segnale elettrico ad impulsi con intensità proporzionale all’intensità luminosa.

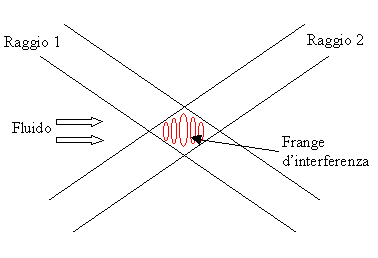
Figura 23. Schema di funzionamento Laser Doppler

Analizzando con un oscilloscopio il segnale ottenuto, osserviamo una serie di picchi che corrispondono al passaggio di particelle attraverso la zona di interferenza.

Dalla lunghezza d’onda e dalla frequenza possiamo risalire alla velocità del fluido.

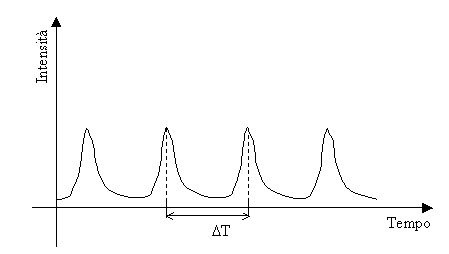
Figura 24. Segnale prodotto dal fotomoltiplicatore

Un problema sta nel riuscire a mandare i raggi all’interno del condotto cosa non molto facile nella maggior parte dei casi, inoltro il fluido in esame non deve essere limpido, perché se lo fosse si verificherebbero dei problemi nella determinazione del verso delle particelle.

Ci viene in aiuto un espediente, quello di inserire un prisma che suddivide in due raggi identici un raggio iniziale, successivamente uno dei due, lo si fa passare attraverso una Cella di Bragg, di modo che aumenti la sua frequenza di 40 MHz, facendo ciò le frange non sono ferme ma bensì in movimento.

Senza l’effetto della Cella di Bragg non si riuscirebbe nemmeno a determinare il verso del movimento del fluido nel condotto. Quando il fluido è in movimento si ha l’effetto Doppler dovuto al contemporaneo movimento sia del fluido che delle frange.

Se il fluido è fermo la f₀ = 40 MHz se la frequenza n di emissione degli impulsi luminosi dovuti alle particelle è maggiore di 40 MHz significa che la particella fotoluminescente e quindi con essa il fluido si sta muovendo in senso opposto rispetto al verso di scorrimento della frange, in verso concorde con le frange se la frequenza risultasse minore di 40 MHz.

Risulta essere è uno strumento di altissima precisione nella misura della velocità, che non richiede calibratura e che riesce ad analizzare un’area ristrettissima, praticamente puntiforme, del condotto; quindi dotato di un’altissima risoluzione spaziale, poiché la misura viene effettuata nel punto d’intersezione dei raggi laser.

Infine è da notare come appunto grazie alla natura stessa della radiazione luminosa il flusso che viene esaminato non viene contaminato in alcun modo.

Trasduttore di tipo magnetico

Si avvolgono delle spire attorno al condotto e vi si fa scorrere una corrente variabile nel tempo in maniera tale che nel condotto vi sia un campo magnetico oscillante.

Questo campo magnetico viene perturbato cioè si genera una forza elettromagnetica dal passaggio di fluido paramagnetico nel condotto come ad esempio l’acqua. Dalla formula :

dove A è la sezione del condotto E_m è la forza elettromotrice K_n è la costante di proporzionalità H_n è il campo magnetico applicato e da misure dell’intensità della perturbazione è possibile risalire alla velocità e quindi alla portata del fluido .

Risulta evidente dalla descrizione il limite del funzionamento di questo trasduttore: esso funziona solamente in presenza di fluido paramagnetico.

Trasduttore ad ultrasuoni

Questo traduttore si realizza facendo due minuscoli fori nel condotto ed iniettando un’onda sonora a una frequenza n_o nel primo foro. Misurando la frequenza n_D del suono dal secondo foro per mezzo di un microfono si riesce a risalire alla velocità W del fluido ed alla sua direzione sfruttando l’effetto Doppler. Infatti l’onda sonora iniettata nel primo foro si propaga nel fluido che se è fermo non ne influenza la propagazione, quindi si avrà n_D uguale a n_o; se invece il fluido si sta’ muovendo si misurerà al secondo foro una variazione della frequenza del suono che è direttamente proporzionale alla velocità W del fluido.

Dal confronto fra n_o e n_D si ha che se n_D > n_o allora il fluido si sta muovendo con lo stesso verso di propagazione del suono, mentre se n_D < n_o allora il verso di propagazione è contrario a quello del suono. Per comprendere meglio questo concetto è bene illustrare un esempio chiarificatore: consideriamo un treno che fischia, se esso si sta avvicinando a noi si sente il suono salire in frequenza, mentre se esso si sta allontanando il suono diminuisce in frequenza; inoltre la variazione di frequenza è tanto maggiore quanto maggiore è la velocità del treno.

Un importante vantaggio del trasduttore ad ultrasuoni è quello di poter analizzare la composizione del fluido: iniettando un suono di brevissima durata misuro il tempo che quest’ultimo impiega ad arrivare al microfono; ho così la velocità v di propagazione del suono nel liquido:

Essendo v funzione della composizione del fluido è possibile ottenere la composizione stessa.

Questo strumento non consente un’alta precisione nella misura della velocità W del fluido e quindi della portata; ciò implica che il suo utilizzo è sconsigliato in processi nei quali è fondamentale il preciso controllo del tempo di percorrenza del fluido nel tubo, quale ad esempio la pastorizzazione UHT, nella quale è fondamentale che il latte venga riscaldato ad un’alta temperatura per un tempo preciso altrimenti si ha la “cottura” del latte stesso.