Isolamento di una parete
Trattando un problema di conduzione
del flusso di calore attraverso una resistenza termica ci si può rifare al ben
noto caso del flusso di corrente che attraversa una resistenza elettrica
essendo i due sistemi analoghi, cioè retti da equazioni simili, intercambiabili
tra loro con la semplice accortezza di sostituire i simboli delle grandezze
coinvolte nel sistema.
Il fenomeno conduttivo
attraverso una parete è di tipo lineare ma studiando un sistema che richieda
l’applicazione di questo modello è necessario introdurre una correzione che dà
ragione dei fenomeni convettivi non lineari che si instaurano nelle vicinanze
della parete stessa. A questo scopo introduciamo il modello dello strato limite
termico che ci permetterà di considerare adeguatamente i fenomeni prima citati.
Lo strato limite
termico è definito come il luogo dei punti entro il quale la variazione di
temperatura temperatura è pari al 99% Tambiente
Ovvero
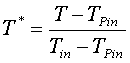
Naturalmente una forma analoga vale per il
calcolo dello Slt esterno
Strato limite Termico
|
Lo strato limite
termico è definito come il luogo dei punti entro il quale la variazione di
temperatura temperatura è pari al 99% Tambiente Ovvero
Naturalmente una forma analoga vale per il
calcolo dello Slt esterno |
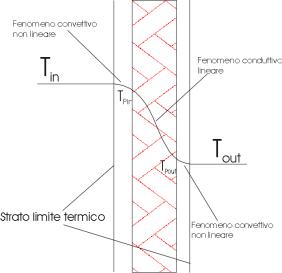
Figura 1- Strato limite termico
Dentro lo Strato limite
termico è localizzata una “resistenza termica” non lineare che può essere
valutata con una pseudo-legge di Fourier
![]() (1)
(1)
quindi
![]() (1.1)
(1.1)
Il termine h viene chiamato coefficiente di
adduzione ed è in realtà somma del coefficiente di convezione e quello di
irraggiamento
![]() (2)
(2)
Da una verifica dimensionale è immediato
verificare che
![]() (3)
(3)
In considerazione della (3) appare quindi
scorretto il nome di coefficiente essendo questo riservato, secondo le norme
del Sistema Internazionale, alle sole grandezze adimensionali
I valori dei coefficienti di adduzione da utilizzare in fase di progetto di impianti di isolamento sono quelli tabulati nelle norme UNI come prescritto dalla legge 10/91.
Fatte queste premesse
possiamo ora illustrare il modello utilizzato per il calcolo del flusso termico
attraverso la parete di Fig.1
Il sistema equivale a una
serie di tre resistenze (ricordando quanto detto sull’analogia di due sistemi
fisici) così schematizzabile:
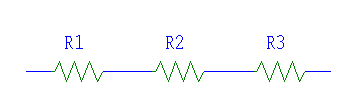
Quindi il flusso termico può essere calcolato come:
![]() (4)
(4)
Consideriamo in questo caso una superficie
unitaria per alleggerire la notazione e riscriviamo le resistenze in funzione
dei parametri del sistema:
![]() ,
, ![]() ,
, ![]() e di conseguenza
l’equazione per il flusso termico:
e di conseguenza
l’equazione per il flusso termico:
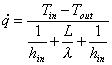 (5)
(5)
Quest’ultima offre una valutazione più accurata di
un modello che considera semplicemente il trasporto conduttivo che si verifica
all’interno della parete. Queste considerazioni sono valide per approssimare un
sistema del nel quale la Tp ,
ovvero temperatura di parete, è incognita. Discutiamo alcuni esempi che possano
chiarire l’uso del modello.
Problemi di esempio
- Si calcoli il
flusso termico attraverso una parete di mattoni di spessore pari a 0.25m e
area di 10 m2 con un
coefficiente di conduzione l=1 W/mk sapendo che hin=8
W/m2K e hout=20 W/m2K. Le
temperature dell’ambiente sono Tin=20oC e Tout=0oC
Ricordando quanto detto in precedenza la soluzione
del problema è immediata sostituendo i dati nella (5), si ha quindi
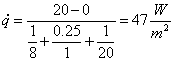
tenendo conto della superficie in oggetto
![]()
- Tenendo conto
dei dati dell’esercizio precedente si calcoli ora la potenza necessaria a
riscaldare un edificio di forma cubica (quattro pareti più il tetto di caratteristiche
analoghe alla parete dell’esercizio 1) di area totale A=50m2 e
nelle stesse condizioni di temperatura.
Considerata la superficie totale calcolo il calore disperso attraverso le
pareti:
![]()
Questa tuttavia non è la potenza necessaria a riscaldare l’edificio poiché
è necessario valutare anche la quantità di calore necessaria a riscaldare
l’aria che, secondo normativa, và introdotta ogni ora nell’ambiente.
Il volume dell’edificio è pari a V=1000m3 e, trattando di
un’abitazione residenziale, il ricambio d’aria deve essere pari a 0.25V/h
ovvero Varia=300m3/h. Essendo introdotta dall’esterno
avrà una temperatura di 0oC. La potenza necessaria a scaldare tale
volume d’aria è data da
![]() dove M è la portata in massa
dove M è la portata in massa
La massa dell’aria in questione si può facilmente ricavare conoscendo la
sua densità r=1.2Kg/m3 e sapendo che Cp=1000 J/Kg*K ottengo per Qv
un valore di
![]()
Non solo dello stesso ordine di grandezza della potenza dispersa attraverso
le pareti ma anche confrontabile per valore numerico. In fase di progetto
l’impianto di riscaldamento andrà quindi dimensionato per fornire una potenza
pari alla somma di Q+QV, nell’ordine quindi di 4kW.
La normativa prevede valori minimi di ricambio d’aria, espressi in percentuale del volume dell’ambiente, funzionalmente all’uso cui è adibito un edificio. 0.25V/h per edifici residenziali (come quello considerato nell’esercizio), 1V/h per edifici commerciali e uffici, 2V/h per edifici scolastici o ambienti pubblici affollati (i.e.: cinema, discoteche).
-
Si calcoli la potenza dissipata attraverso il rivestimento di una caldaia schematizzato dalla figura seguente:DATI DEL PROBLEMA
Ta=100oC Tb=0oC
sa=0.05m sb=0.1m
S1=1m2 S2=2m2
la=60 W/mK
lB1=1 W/mK lB2=0.2 W/mK
A=acciaio
B1=cemento B2=isolante
ha=200 W/m2K hb=10 W/m2K
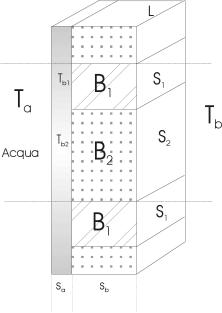
Figura 2 - Sezione della parete
Come appare dalla figura
la parete è costituita da una lastra d’acciaio a contatto con l’acqua e da un rivestimento
esterno di travetti di cemento alternati ad altri di materiale isolante. In
questa situazione risulta particolarmente comodo applicare il principio di
equivalenza con le reti elettriche. Una prima schematizzazione del sistema può
essere la seguente:
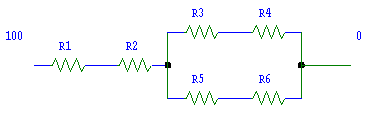
Figura 3 - Le temperature di parete di cemento ed isolante sono considerate uguali
R1 è la resistenza dello
strato limite termico (relativo alla parete d’acciaio), R2 la resistenza della
parete d’acciaio, R3 e R5 le resistenze delle pareti di cemento e di isolante,
R4 ed R6 le resistenze dello strato limite termico (relativo alla parete di
travetti) differenziato a seconda dei due materiali
Per una maggiore
precisione si dovrebbe considerare il fato che ![]() , ovvero che le temperature di parete, per cemento ed
isolante, non sono uguali; questo corrisponde alla nuova rete
, ovvero che le temperature di parete, per cemento ed
isolante, non sono uguali; questo corrisponde alla nuova rete
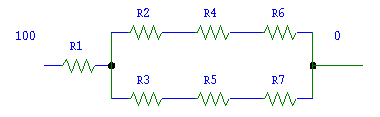
Figura 4
R2 ed R3 sono ora due
diverse resistenze in considerazione del fatto che, pur partendo dalla
temperatura comune della parete di acciaio, le temperature di arrivo (per le
pareti di cemento e isolante) sono diverse.
Continuando nello stesso
senso possiamo raffinare ulteriormente la schematizzazione come nella Fig. 5
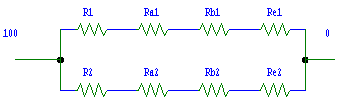
Figura 5
Anche questa rete però è
solo un’approssimazione della realtà fisica, non fornisce quindi il risultato
reale poiché non tiene conto, per esempio, della conduzione tra gli strati B1
e B2 che andrebbe schematizzato come in fig. 6
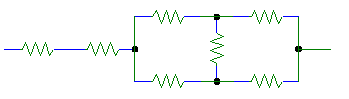
Figura 6 – Viene considerata anche la conduzione tra gli strati affiancati
Il modello che offre la
maggio semplicità di calcolo è quello rappresentato in Fig. 5. Procediamo
quindi con lo sviluppo dei conti (per la sola zona compresa tra le due linee
orizzontali di Fig. 2) tenendo presente che:
Resistenza di convezione acqua ![]()
Resistenza di conduzione acciaio (su cemento) 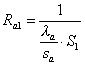
Resistenza di conduzione cemento 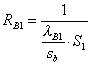
Resistenza di convezione aria (su cemento) ![]()
Resistenza di convezione acqua ![]()
Resistenza di conduzione acciaio (su isolante) 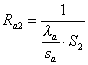
Resistenza di conduzione isolante 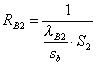
Resistenza di convezione aria (su isolante) ![]()
Calcoliamo la potenza dissipata nel primo ramo
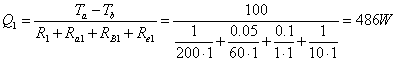
e quella nel secondo ramo
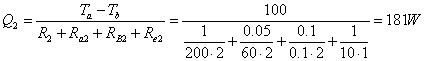
La potenza totale dissipata è quindi pari a 667W
Come già detto in
precedenza questa è solo un’approssimazione del risultato reale poiché il modello schematizza grandezze distribuite
con parametri concentrati
Con i dati del problema posso anche calcolare le varie temperature di parete. A titolo di esempio calcoliamo la temperatura sul pannello di cemento (come “caduta” del flusso parziale sulla resistenza equivalente del travetto di cemento)
![]()
e,
analogamente, per l’isolante
![]()
Dati
che danno un’idea dell’importanza della scelta dei materiali quando si renda
necessario un isolamento termico.
Strumenti per la misura della capacità
termica
Esistono principalmente
due metodi per la misura della capacità termica: il metodo della lastra piana
doppia e mediante il termoflussimetro. Per entrambi la misura viene effettuata
su di un provino normalizzato, ovvero una lastra quadrata (di lato 500 mm) del
campione di spessore variabile. A titolo di esempio riporto le condizioni
richieste ad un campione dal laboratorio di misura dell’università di Padova
[…]
3. I campioni da sottoporre a prova devono avere le seguenti caratteristiche:
· Spessore compreso tra 3 e 12 cm;
· Dimensioni 0,5m ´ 0,5 m;
· Superfici maggiori piane, levigate entro 0,2 mm oppure tali da aderire ad un piano quando
sottoposte alla pressione di 1 kPa (circa 100 kg/m2);
· Superfici maggiori parallele entro il 2% dello spessore;
· Densità non superiore a 500 kg/m3.
4. Ciascun campione dovrà essere identificato con una “Designazione del campione” (nome
commerciale del prodotto, sigla di campionamento, etc.) e dovrà essere accompagnato da una
“Descrizione del campione” che identifichi in non più di due righe la natura chimico-fisica
del campione e la tecnica di produzione. Sia la “Designazione del campione” che la
“Descrizione del campione” figureranno nel frontespizio del certificato di prova come
indicazioni fornite dal Committente. Dette informazioni verranno fornite dal Committente
con la compilazione della scheda SPC.
5. Per ogni prova il Committente deve specificare:
· la temperatura media alla quale la misura stessa dovrà essere effettuata (normalmente 20 °C),
tenendo presente che la temperatura del lato freddo del campione non potrà essere inferiore a
–15 °C, mentre quella del lato caldo non potrà superare i 60 °C;
· la differenza di temperatura tra le facce delle provette (normalmente tra i 10 °C e 20 °C);
· la temperatura massima alla quale il campione può essere essicato in stufa a circolazione
d’aria calda o, in alternativa, il condizionamento a 23 ± 1 °C e 50 ± 10 % di umidità relativa;
· la data di produzione , se significativa ai fini della prova.
[…]

Figura 7 - Il banco per la determinazione dello spessore del provino

Figura 8 - Provini imbustati, pronti per l’esecuzione della prova
Metodo della lastra piana doppia
È il metodo di misura più preciso e costoso e che richiede il tempo
maggiore per la sua attuazione. Di seguito vediamo lo schema
dell’apparecchiatura usata per questo tipo di misura
1.sezione centrale della piastra calda 2.anello di guardia della piastra calda 3.provino 4.piastra fredda 5.secondo anello di guardia 6.isolamento ai bordi 7.secondo isolamento di guardia 8.flusso di aria raffreddante NB: il flusso d’aria può essere sostituito da un
bagno termostatico
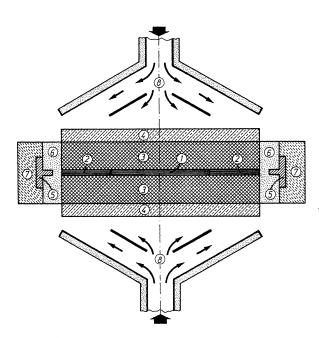
Figura 9 - Schema dell’apparecchiatura a lastra piana doppia con doppio anello di
guardia
La generazione del calore
è delegata ad una resistenza (1 nella figura 9) per effetto Joule. Di conseguenza
ho a disposizione il dato preciso del calore fornito ai provini.
Nell’apparecchiatura
rappresentata i vettori Q (il flusso di calore) sono esattamente
perpendicolari alla lastra (per la sua simmetria costruttiva). Facendo
riferimento alla relazione
![]() (6)
(6)
posso calcolare senza problemi il coefficiente di
conducibilità termica l essendo esso l’unica incognita del problema (dove s è lo spessore del
provino)
Misura mediante termoflussimetri (ISO
8301:1991; UNI 7891:1978)
Questo metodo è meno
preciso ma molto più economico del precedente. Si possono avere buone
precisioni di misura tarando spesso i termoflussimetri utilizzati.
Il termoflussimetro è un
materassino di un materiale di cui siano note le caratteristiche sul quale è
avvolta a spirale una termocoppia differenziale. Le f.e.m. della termocoppia
sono in serie quindi, avendo a disposizione un buon numero di avvolgimenti e
avendo cura di tarare lo strumento di frequente (a causa delle variazioni delle
caratteristiche del materiale che compone il materassino), è comunque possibile
ottenere una buona precisione. Di seguito è mostrato lo schema di
un’apparecchiatura abbastanza sofisticata per la misura di l con questo metodo
1.
termoflussimetro superiore, lato freddo 2. termoflussimetro
inferiore, lato caldo 3. piastre metalliche 4. isolamento unità
riscaldante o raffreddante 5. provino 6. molle di supporto
dell'unità raffreddante superiore 7. meccanismo di
abbassamento per l'unità raffreddante superiore 8. ventilatore per la
circolazione dell'aria interna 9. spira raffreddante per
il controllo del punto di rugiada dell'aria interna 10. resistenza riscaldante
per il controllo della temperatura dell'aria interna 11. gabbia interna per
convogliare il flusso d'aria interna condizionata attorno
all'apparecchiatura 12. cabina isolata che
racchiude l'apparecchiatura 13. motore del ventilatore 14. isolamento dei bordi
del provino
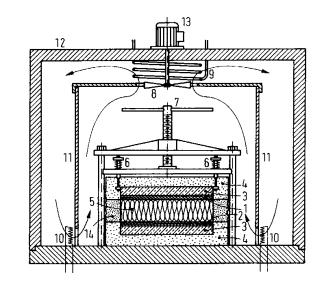
Figura 10 - Schema dell’apparecchiatura a doppio
termoflussimetro e
singolo provino
Il segnale elettrico
trasmesso dalla termocoppia è proporzionale a DT tra i capi del termoflussimetro
![]()
Utilizzando
la (6) ora che conosco Q posso ricavare il valore di l