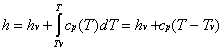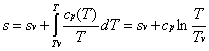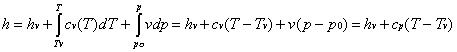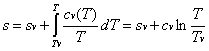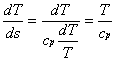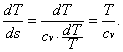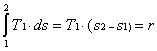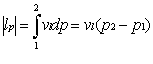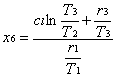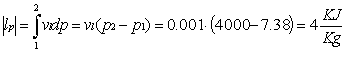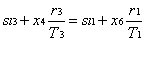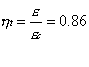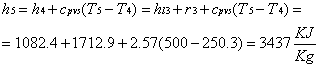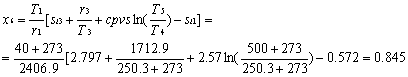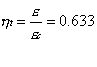Figura 1
Tabella 1
![]()
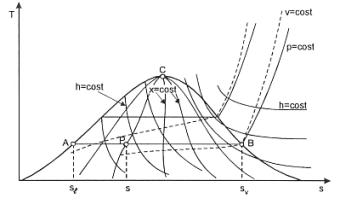
Figura 2
Figura 3
![]()
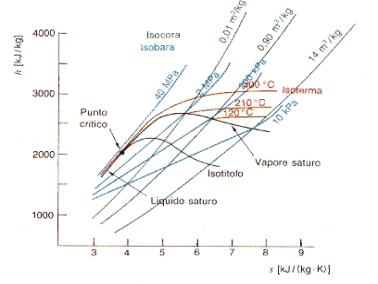
Figura 4
Tabella 2
Figura 7
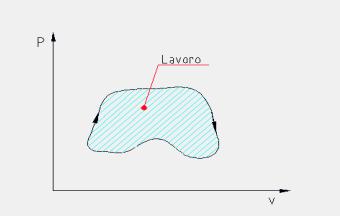
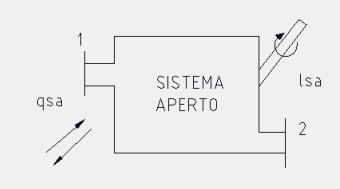
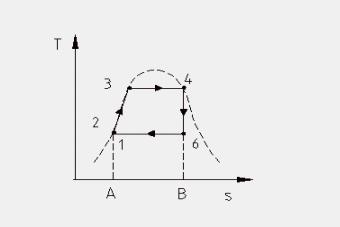
L’area sottesa ad una generica trasformazione reversibile rappresenta, nel piano (T, s), il calore scambiato dall’unità di massa della sostanza soggetta alla trasformazione.
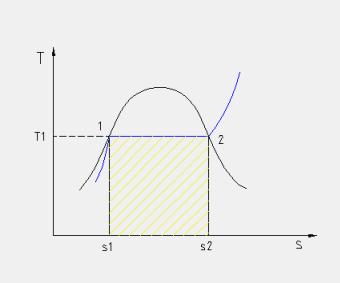
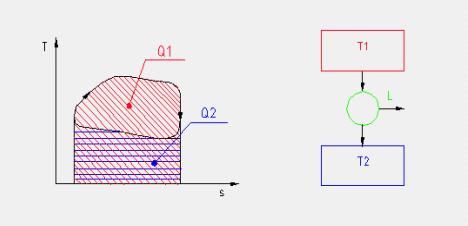
Applicando il primo principio della termodinamica alla trasformazione ciclica mostrata in figura 7 (ricordiamo che in tutte le trasformazioni cicliche di una sostanza la variazione dell’energia interna della stessa è nulla) abbiamo che:
Figura 8
Figura 9
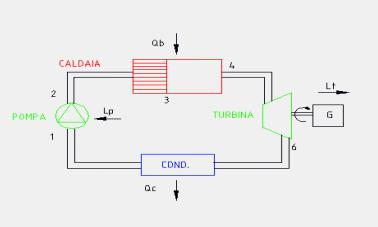
Analizziamo una ad una le fasi del ciclo:
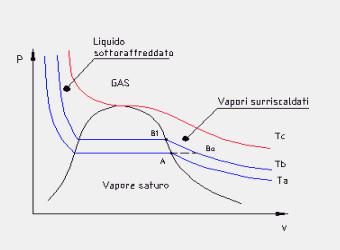
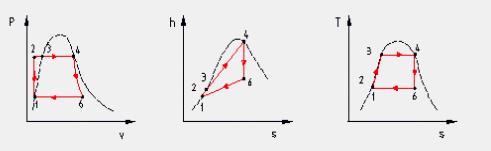
1 —> 2 Compressione secondo una trasformazione adiabatica reversibile (quindi isoentropica) dell’acqua di alimento fino alla pressione esistente nella caldaia. Dai diagrammi termodinamici (Figura 9) si vede come nella nostra trattazione scegliamo di fare alcune sempificazioni, infatti:
· Durante la compressione del fluido nella pompa abbiamo considerato nulla la variazione di volume. Nel diagramma (P,v) i punti uno e due sono uniti da un segmento verticale.
· Sempre nella compressione del fluido consideriamo nulle le varazioni di temperatura, entalpia ed entropia. Nei diagrammi (h,s) e (T,s) i punti uno e due coincidono.
Ai fini pratici comunque le approssimazioni introdotte sono accettabili.
2 —> 3 Inizio del riscaldamento, a pressione costante, dell’acqua fino alla temperatura di saturazione corrispondente alla pressione esistente nella caldaia (stato di liquido saturo). Dai diagrammi vediamo che nel passaggio da due a tre variano tutte le grandezze termodinamiche dell’acqua, ad eccezione, come detto, della pressione.
3 —> 4 Vaporizzazione, sempre a pressione costante, dell’acqua fino allo stato di vapore saturo secco (titolo x4 =1).
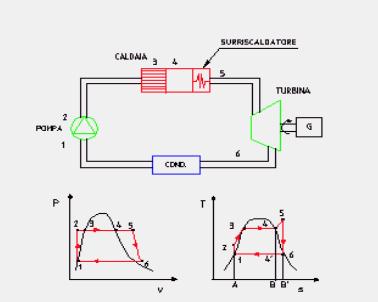
4 —> 6 Espansione adiabatica reversibile (e quindi isoentropica) del vapore in turbina in modo da produrre lavoro. Nelle centrali termoelettriche il lavoro sviluppato in turbina viene sfruttato da un generatore di energia elettrica ( in Figura 8 indicato con la lettera G).
6 —> 1 Sottrazione di calore, a pressione costante, nel condensatore con la condensazione del vapore scaricato dalla turbina fino a far ritornare l’acqua nello stato iniziale del ciclo.
![]()
Il condensatore non è fondamentale per chiudere il ciclo, si potrebbe infatti
scaricare il vapore nell’atmosfera ed alimentare continuamente il ciclo con
nuova acqua immettendola nella pompa (punto uno). Cosi’ facendo però si
andrebbe incontro ad elevati costi per il trattamento chimico dell’acqua di
alimento. Infatti nelle installazioni moderne l’acqua deve essere sempre
demineralizzata e degassata per prevenire depositi incrostanti e fenomeni di
corrosione.
Figura 10
Figura 11
Il calore qb è rappresentato nel diagramma (T,s) riportato dall’area A-1-3-4-B-A, qc dall’area A-1-6-B-A, lciclo si può ottenere come differenza delle due aree scritte è quindi a sua volta rappresentato dall’area 1-3-4-6-1, negli impianti reali vengono relizzati tutti gli accorgimenti tecnici atti ad aumentare questa area (noi vedremo il surriscaldamento).
Per valutare l’efficienza del ciclo Rankine calcoliamone il coefficiente economico, definito come il rapporto tra il lavoro prodotto e il calore assorbito:
![]()
Il lavoro scambiato dal ciclo di Rankine può essere espresso anche come
![]()
Quindi
![]()
Arrivati a questo punto della trattazione facciamo notare che alcuni testi chiamano il ciclo Rankine descritto finora ideale. Questo aggettivo si spiega con il fatto che abbiamo considerato tutte le trasformazioni del ciclo reversibili. Nella realtà occorre tenere presente che le trasformazioni, di compressione del liquido nella pompa e di espansione del vapore in turbina, sono ancora adiabatiche, ma sono irreversibili. Si tiene conto di ciò attraverso i rendimenti interni della turbina e della pompa. Non entreremo comunque nel dettaglio di questa trattazione. E’ però importante non equivocare il termine ideale, l’analisi energetica da noi condotta è assolutamente esatta solo che non tiene conto dei rendimenti a cui abbiamo accennato sopra.
Esempio 1:
Figura 12
Nello schema dell’impianto possiamo vedere che la
caldaia presenta un nuovo componente, che non è altro che un serpentino riscaldatore . Scegliamo ora
di distinguere i punti uno e due sul diagramma temperatura entropia, ovvero
nella compressione il liquido subisce un piccolo aumento di temperatura. La
scelta non è legata all’analisi del
surriscaldamento.
Dai diagrammi termodinamici possiamo vedere come il surriscaldamento porti a due importanti miglioramenti:
1-Aumento del lavoro complessivo compiuto dal ciclo dell’area 4-5-6-4’-4 (vedi figura 12), mentre il calore qb fornito alla caldaia (che verrà poi trasferito al vapore) aumenta dell’area 4-5-B’-B-4. Essendo il rapporto di queste due aree maggiore del rapporto tra il lavoro del ciclo e il calore fornito per il resto del ciclo, ne risulta un aumento complessivo del rendimento del ciclo Rankine.
2-La trasformazione 5-6 avviene quasi interamente nella zona del vapore surriscaldato. Questo riduce la presenza di liquido condensato nella turbina, comportando una riduzione del rischio di rottura della stessa. Nei calcoli termodinamici avremo un titolo della miscela nel punto sei molto più vicino a uno.
Tramite un esempio numerico vediamo le modifiche da apportare all’analisi energetica.
Esempio 2:
Utilizziamo ancora i dati dell’esempio precedente.
Nella reatà il surriscaldamento è un vero miglioramento del ciclo, dal punto di vista del secondo principio della termodinamica poiché il calore fornito alla caldaia qb viene sfruttato molto più efficacemente.
Esaminiamo il diagramma che esprime l’andamento della temperatura dei fumi in funzione del calore che questi forniscono alla caldaia.
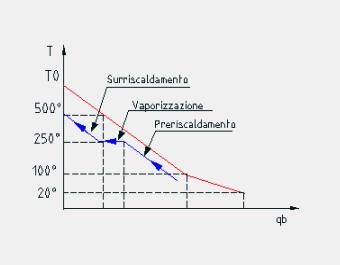
Figura 13
Dal diagramma si vede che il ciclo di Rankine con surriscaldamento è molto brillante, dal punto di vista del secondo principio della termodinamica. Viene infatti sfruttato al meglio il processo di combustione, minimizzando l’aumento di entropia, rappresentato dall’area compresa tra la curva riguardante la trasformazione 2-5 del ciclo Rankine e il diagramma temperatura calore dei fumi. Possiamo inoltre notare che l’unico modo per sfruttare tutto il potenziale di calore dei fumi è una successione infinita di cicli di Carnot, uno per ogni variazione infinitesima di temperatura. Questo processo non è fisicamente realizzabile quindi il ciclo di Carnot lavora bene solo tra due serbatoi di calore a temperatura costante.