Esercizi sul moto dei fluidi
·
Richiami teoria
·
Proposte di esercizi
·
Appendice
Richiami Teoria
·
N° di Reynolds : ![]() (1)
(1)
Questa formula ci dice che la transizione da regime
laminare a regime turbolento dipende da quattro grandezze: velocità del liquido
(w), densità (![]() ), viscosità del fluido (
), viscosità del fluido (![]() ) e diametro del condotto (D).
) e diametro del condotto (D).
In particolare se Re è minore di 2100 abbiamo un moto laminare, se Re è maggiore di 4000 abbiamo un regime turbolento, mentre all’interno di questo intervallo ci troviamo in una zona instabile dove non è possibile prevedere il comportamento del fluido.
Considerando la viscosità cinematica ![]() allora la formula (1)
diventa :
allora la formula (1)
diventa : ![]()
·
Scabrezza relativa : ![]()
Dove ![]() è la scabrezza del
tubo e D è il suo diametro
è la scabrezza del
tubo e D è il suo diametro
·
Fattore di attrito :
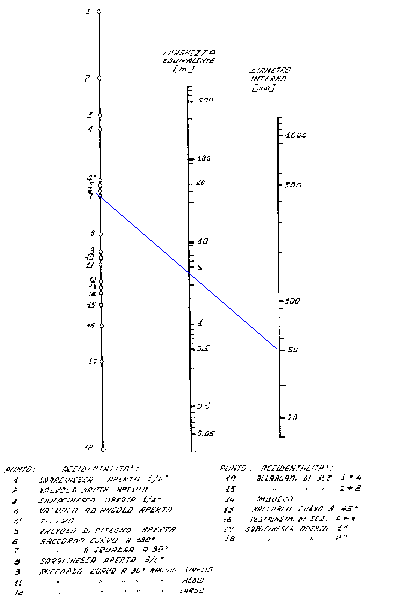
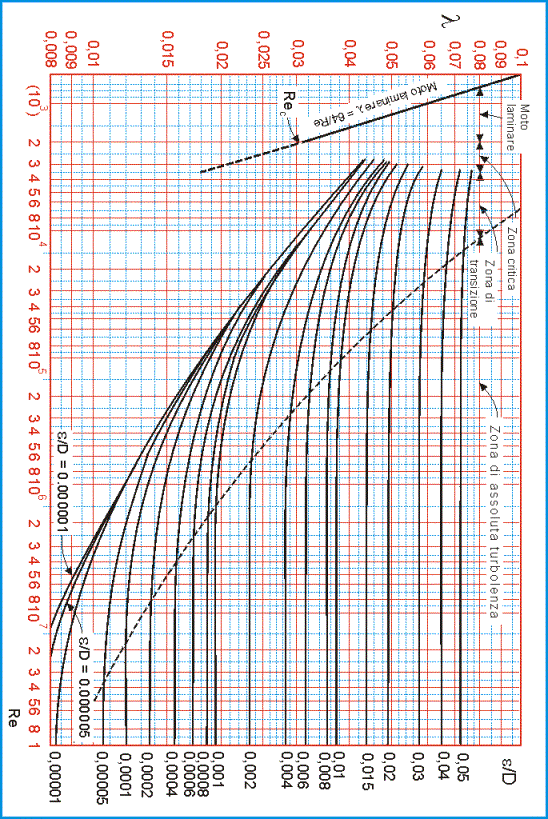
Sapendo la scabrezza relativa ed il n° di Reynolds tramite il diagramma di Moody (vedi appendice) possiamo ricavare il fattore di attrito.
Analiticamente abbiamo la seguente formula
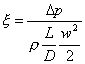
da cui si ricava la perdita di carico
![]()
· Perdite di carico distribuite :
![]()
Nel caso di regime laminare e condotto liscio a sezione circolare costate si ha
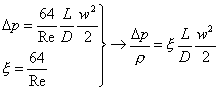 (2)
(2)
· Perdite di carico concentrate :
![]() (3)
(3)
dove ![]() è il coefficiente di
perdita concentrate che varia a seconda del tipo di ostacolo o discontinuità
presente nel condotto (vedi appendice).
è il coefficiente di
perdita concentrate che varia a seconda del tipo di ostacolo o discontinuità
presente nel condotto (vedi appendice).
Quindi per calcolare le perdite di carico totali bisogna sommare sia quelle concentrate (3) che quelle distribuite (2):
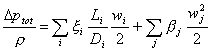 (4)
(4)
· Lunghezza equivalente :
Per le perdite concentrate possiamo introdurre il concetto di lunghezza equivalente; semplicemente si uguaglia la perdita concentrata ad una perdita distribuita lungo un tubo di opportuna lunghezza.
La lunghezza equivalente, quindi, varia a seconda delle discontinuità presenti nel condotto e si ricava dall’apposito nomogramma (vedi appendice).
In tal modo, nel calcolo delle perdite totali, è possibile eliminare la dipendenza dalle perdite concentrate.
· Diametro equivalente:
Ci permette di studiare il moto dei fluidi in condotti di qualsiasi forma, non solo circolare, considerandoli come tali; definiamo il diametro equivalente come
![]()
dove A è l’area della sezione del condotto e Perimetro-bagnato è il perimetro che il liquido tocca all’interno del condotto.
Consideriamo per esempio un tubo quadrato di lato ![]()

ll
![]()
![]()
· Equazione di Bernoulli (bilancio energetico):
Normalmente per la risoluzione degli esercizi viene utilizzata una equazione più semplice di quella di Navier: l’equazione di Bernoulli, che esprime il bilancio energetico tra due sezioni del condotto.
Quest’ultima si ricava integrando, a regime stazionari, l’equazione di Navier sul tubo di flusso considerato
![]()
Dove R indica le perdite di carico ![]() espresse nella (4)
espresse nella (4)
· Equazione di continuità:
Consideriamo un tubo Come in figura
![]()
![]()
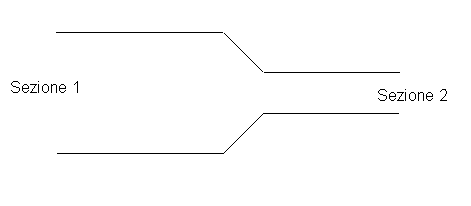
Nelle due sezioni considerate la portata massica deve essere la stessa, quindi
![]()
![]()
![]()
![]()
dove D è il diametro delle rispettive sezioni del condotto.
Si nota quindi come diminuendo il diametro debba aumentare la velocità affinché la portata massica rimanga invariata.
Proposte di esercizi
Esercizio 1
Un tubo di lunghezza ![]() e con un diametro
e con un diametro ![]() ha una portata
ha una portata ![]() di acqua ad una
temperatura di 27°C.
di acqua ad una
temperatura di 27°C.
Sapendo
che la potenza della pompa è costante (![]() ), se l’acqua viene raffreddata fino a 5°C, varia la portata ?
), se l’acqua viene raffreddata fino a 5°C, varia la portata ?
Svolgimento
Prima
di tutto bisogna cercare la viscosità dinamica (![]() ) e la densità (
) e la densità (![]() ) dell’acqua a 27°C e ad una atmosfera sulle apposite tabelle
per ricavare la viscosità cinematica (
) dell’acqua a 27°C e ad una atmosfera sulle apposite tabelle
per ricavare la viscosità cinematica (![]() )
)
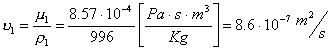
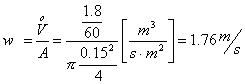
![]()
Conoscendo
![]() e considerando la scabrezza relativa del tubo
e considerando la scabrezza relativa del tubo ![]() vado a vedere il
corrispondente fattore di attrito
vado a vedere il
corrispondente fattore di attrito ![]() sul diagramma di
Moodi (vedi appendice) e trovo
sul diagramma di
Moodi (vedi appendice) e trovo
![]()
Ora
cerco le perdite distribuite
![]()
![]()
Quindi
calcolo la potenza della pompa
![]()
Considerando
che la pompa ha una rendita ![]() , la potenza efficace risulta
, la potenza efficace risulta
![]()
Riducendo
la temperatura a 5°C avrò altri valori di viscosità dinamica e densità, quindi
cambierà anche la viscosità cinematica ed il numero di Reinolds.
![]()
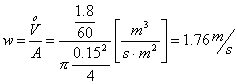
![]()
Ora
andando ancora sul diagramma di Moodi si ricava il fattore di attrito relativo
a ![]() ed a
ed a ![]()
![]()
Notiamo
che il fattore di attrito è cresciuto, quindi la prevalenza della pompa
dovrebbe essere cresciuta per aver mantenuto la stessa portata, ma per ipotesi
abbiamo che la potenza della pompa è costante quindi deve essere calata la
portata.
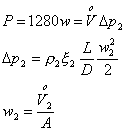
Poiché
![]() <
<![]() segue che anche
segue che anche ![]() <
<![]() (ricordiamo che avevamo ipotizzato la stessa velocità alle
due temperature), tuttavia non conosco la nuova velocità.
(ricordiamo che avevamo ipotizzato la stessa velocità alle
due temperature), tuttavia non conosco la nuova velocità.
Quindi
ho due variabili, portata e velocità; in questo caso è necessario innescare un
processo iterativo, si fissa un valore di una variabile e si ricava la seconda
incognita.
·
Tengo costante la
velocità ![]()
![]()
![]()
![]()
Questi
calcoli naturalmente sono errati poiché ho tenuto costante la velocità; ora
fisso una nuova velocità
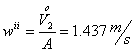
ora
rifaccio i calcoli con la nuova velocità
![]()
![]()
![]()
![]()
Questo
risultato non va bene, abbiamo ottenuto un valore che supera la portata
iniziale, questo processo iterativo non converge al valore cercata. In questo
caso bisogna quindi tenere costante la prevalenza.
·
Tengo costante la
prevalenza ![]()
Ora ricavo ![]()
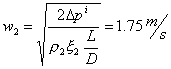
quindi calcolo la nuova prevalenza ed impongo che
la potenza sia la stessa.
![]()
![]()
![]()
A questo punto bisogna ripetere i calcoli col
nuovo valore di ![]() ottenuto.
ottenuto.
N.B.: Spesso è consigliabile tener costante il
termine con esponente minore e far variare il termine con esponente maggiore;
nel nostro caso, infatti, la velocità era elevata al quadrato mentre la
prevalenza no
Esercizio 2
Due
tubi, A e B, posti in serie tra loro, aventi diametro interno rispettivamente DA=5
cm, DB=10 cm e lunghezza LA=180 m, LB=90 m, collegano
due serbatoi con diverse quantità di acqua. La differenza di quota tra i due
peli liberi è H=6 m ed il coefficiente di viscosità cinematica è ![]() .
.
Sapendo che i tubi sono in ghisa (![]() ), determinare la portata.
), determinare la portata.
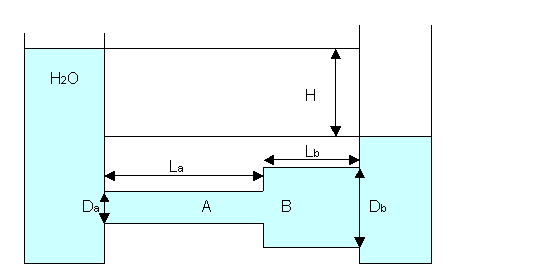
Svolgimento
Prima di tutto scrivo l’equazione di bilancio
dell’ energia (equazione di Bernoulli) tra le due sezioni:
![]()
![]()
![]()
Le velocità sono piccole quindi posso non considerare il 1° termine, inoltre, poiché 6m di dislivello non originano alcuna differenza di pressione posso omettere anche il 3° termine.
Ora devo cercare le perdite distribuite e quelle concentrate (R).
Per le perdite concentrate uso le lunghezze equivalenti che ricavo
dall’apposito nomogramma (vedi appendice), arrivando così alla seguente
espressione
![]() (1)
(1)
Inoltre sappiamo che dobbiamo avere la stessa portata nelle due sezioni
quindi
![]()
![]()
![]()
Andando a sostituire ![]() nella (1) si ottiene
nella (1) si ottiene
![]()
Posso quindi ricavare ![]()
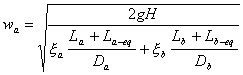 (2)
(2)
Come possiamo notare nell’ equazione
(1) compaiono due incognite, la velocità ed il fattore di attrito; quest’ultimo
dipende proprio, tramite il numero di Reynold, dalla velocità. Quindi per
risolvere il problema dobbiamo innescare un processo iterativo ipotizzando una
“velocità di primo tentativo”.
·
1°
tentativo
![]()
![]()
![]()
Ora posso calcolare i numeri di
Reinolds per ciascuna sezione
![]()
![]()
Sapendo che il tubo è scabro, ricavo
la scabrezza relativa delle due sezioni
![]()
![]()
Ora ricavo facilmente dal diagramma di
Moody i rispettivi coefficienti di attrito delle due sezioni
![]()
![]()
Le lunghezze equivalenti , come gia
detto si ricavano facilmente dal nomogramma poiché le sezioni via via si
raddoppiano.
![]()
![]()
Andando a sostituire tutti i valori
ottenuti nella (2) otteniamo
![]()
![]()
![]()
Quindi la portata sarà
![]()
Poiché la velocità iniziale che
abbiamo supposto (![]() ) è sbagliata bisogna ripetere i calcoli fissando come
velocità di secondo tentativo
) è sbagliata bisogna ripetere i calcoli fissando come
velocità di secondo tentativo ![]() , e continuare con successive approssimazioni fino ad
arrivare al valore esatto.
, e continuare con successive approssimazioni fino ad
arrivare al valore esatto.
Esercizio3
Siano dati due serbatoi di forma
cilindrica, A e B, uguali tra loro, pieni di acqua (![]()
![]() ).
).
Alla loro base vengono applicati tubi
di lunghezza diversa (come in figura).
Dire, dimostrandolo, quale si svuota
per primo.
![]()
![]()
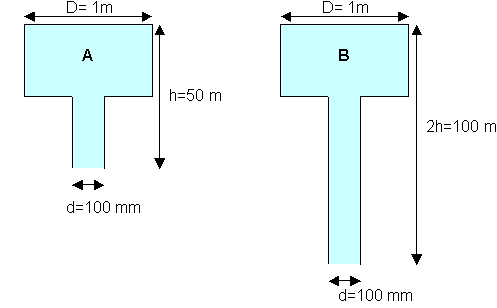
Svolgimento:
Consideriamo
il serbatoio A.
Per
prima cosa cerchiamo le perdite di carico concentrate e distribuite
![]()
![]()
![]()
dove
L è la lunghezza del condotto e ![]() la velocità nella sezione 2.
la velocità nella sezione 2.
Scriviamo
ora l’equazione di Bernoulli, che nel nostro caso diventa
![]()
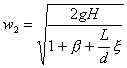
Quindi
si vede che la velocità con cui esce l’acqua è direttamente proporzionale alla
lunghezza del tubo, la velocità di uscita del serbatoio B sara quindi
maggiore di quella del serbatoio A.
Da
queste considerazioni arriviamo alla conclusione che si svuota prima il
serbatoio B
Esercizio 4
Determinare
l’altezza del getto d’acqua di una fontana alimentata da una pompa di
prevalenza ![]() = 4 Bar
= 4 Bar
Dati
L = 6 m
D = 0.08 m
d = 0.02 m
r = 103
Kg/m3
u = m/r = 10-6 m2/s
Per semplicità si considerino I tubi lisci
Svolgimento
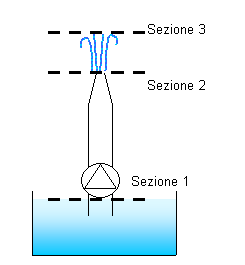
Prima
di tutto applichiamo l’equazione di Bernoulli alle sezioni 1 e 2 indicate in
figura
![]()
![]()
Il
termine ![]() è trascurabile poiché
le due sezioni possono essere considerate entrambe a pressione atmosferica; R
non sono altro che le perdite di carico totali, e guardando il disegno si nota
come
è trascurabile poiché
le due sezioni possono essere considerate entrambe a pressione atmosferica; R
non sono altro che le perdite di carico totali, e guardando il disegno si nota
come ![]() non sia altro che
non sia altro che ![]() .
.
Sfruttando
l’equazione di continuità, uguagliamo le portate massicce nelle due sezioni
![]()
poiché
![]() si ricava
si ricava ![]()
Si
deve quindi risolvere il seguente sistema
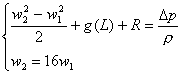
![]()
Ora
dobbiamo calcolare le perdite di carico, in particolare per la perdita di
carico concentrata, data dal restringimento dell’ugello, usiamo le lunghezze
equivalenti, sfruttando l’apposito nomogramma in appendice.
![]()
![]()
![]()
Andando
a sostituire nel sistema R otteniamo ![]() in funzione di
in funzione di ![]()
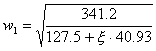
Come
sappiamo per individuare ![]() sul diagramma di
Moody ci occorre il numero di Reynolds . In questo caso non è però possibile
calcolarlo poiche esso stesso dipende dalla velocità.
sul diagramma di
Moody ci occorre il numero di Reynolds . In questo caso non è però possibile
calcolarlo poiche esso stesso dipende dalla velocità.
La
risoluzione di questo problema richiede quindi un processo iterativo.
Per
cominciare possiamo calcolare la velocita che avremmo con coefficiente di
attrito nullo:
![]()
![]()
![]()
Con questo valore di velocità possiamo calcolare
il corrispondente numero di Reynolds:
![]()
Ora con questo valore di Re e sapendo che i tubi
sono lisci dal diagramma di Moody ricavo una nuova ![]()
![]()
Con questo nuovo coefficiente di attrito ripeto i
calcoli trovando una nuova velocità
![]()
Questa nuova velocità differisce di pochissimo
dalla precedente e posso quindi considerarla il mio valore definitivo.
Ritornando al sistema iniziale, calcolo la
velocità nella seconda sezione:
![]()
In fine considero le sezioni 2 e 3. La formula di
Bernoulli si riduce ad una equazione molto semplice, e ricavo facilmente
l’altezza del getto d’acqua:
![]()
Appendice
·
Diagramma di Moody
·
Coefficienti ![]() per le perdite concentrate
per le perdite concentrate
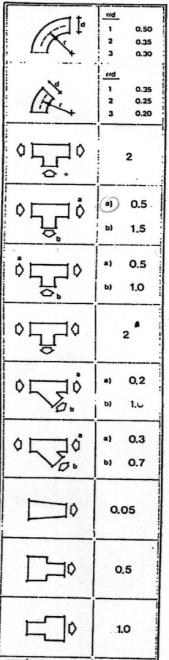
·
Tabella per il
calcolo del diametro equivalente