Diagramma di Moody

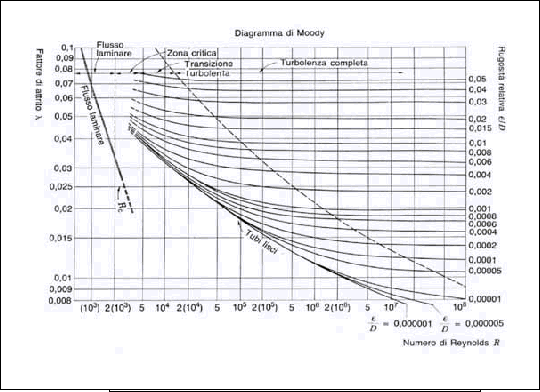
Fig.1 – diagramma di Moody.

Il diagramma di Moody riporta il fattore di attrito x (indicato in Figura 1 con l) in funzione del numero di Reynolds Re, usando come parametro i valori della scabrezza o rugosità relativa . Si ha che:

dove è il fattore di perdite distribuite lungo il percorso e la seconda equazione delle (2) vale soltanto in regime laminare.

Nel diagramma si distinguono quattro zone. Le regione di moto laminare e moto turbolento sono infatti separate da due regioni chiamate zona critica e zona di transizione. La prima rappresenta il limite della zona laminare, cioè quei valori di x e Re per cui il moto è ancora tale ma sta per diventare turbolento. Se si continua a salire con Re (o con ) si raggiunge la zona di transizione, in cui il moto non è più laminare pur non avendo ancora le caratteristiche del regime fortemente turbolento.

E’ importante fare in modo di non lavorare mai in regime di transizione, poiché questo comporta instabilità sul moto del fluido. Se si è in zona di transizione infatti il moto è già turbolento. Le perdite elevate derivanti da questo tipo di moto inducono il fluido a rallentare; ma all’immediata sinistra della zona di transizione nel diagramma di Moody vi è la zona critica, in cui il moto diventa laminare. Le perdite si riducono a causa del nuovo regime di moto del fluido ed esso torna ad accelerare. Questo lo riporta in zona di transizione ed il processo riparte da capo. La velocità del fluido nel condotto continua ad aumentare e diminuire, e ciò è fonte di notevoli disturbi.

Infine è importante osservare come in regime fortemente turbolento il fattore di attrito non dipenda più dal numero di Reynolds, ma soltanto dalla scabrezza relativa.

Perdite concentrate

Sono perdite causate dalla presenza di accidentalità lungo il percorso. Quando il fluido incontra un ostacolo, esso subisce una caduta di pressione, riconducibile al fattore di perdite concentrate

In esso il coefficiente b è chiamato coefficiente di perdite concentrate ed è il fattore (determinato sperimentalmente) che discrimina l’ostacolo in questione: curve strette, convergenze, raccordi ed ogni altro tipo di ostacoli sono caratterizzati da un valore di b differente, come si vede nella Tabella 1.

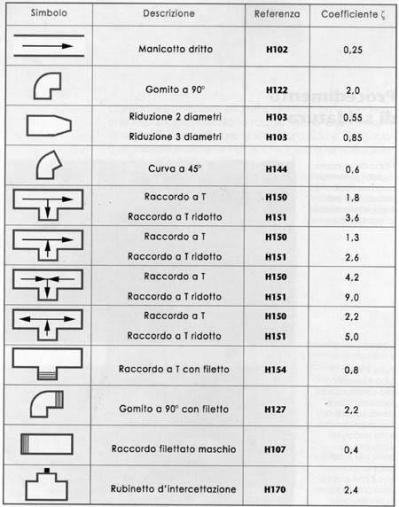
Tab.1 – coefficienti di perdite concentrate.

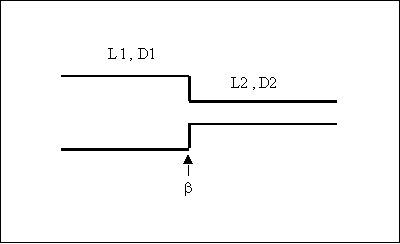
Fig.2 – esempio di perdite concentrate: brusco convergente.

Se per esempio consideriamo il caso di Figura 2 costituito da un brusco convergente, il fattore di perdita totale sarà:

Il primo addendo del secondo membro rappresenta le perdite distribuite nel tratto precedente al restringimento, il secondo quelle nel tratto successivo, mentre il terzo tiene conto delle perdite subite nell’attraversare l’ostacolo. E’ utile osservare che, cambiando sia la scabrezza relativa, sia il numero di Reynolds, e sono diversi. Occorre quindi consultare due volte il diagramma di Moody.

Osservando l’equazione (4) è possibile osservare un’analogia con un circuito elettrico (vedi Figura 3). Le tre perdite di carico sono assimilabili a tre resistenze in serie, le quali sono causa di cadute di potenziale (cioè di pressione) quando sono attraversate dalla corrente I (costituita, nel paragone, dalla portata ).

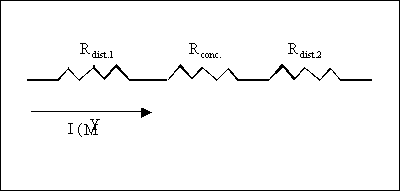
Fig.3 – analogia con un circuito elettrico.

L’analogia tre circuiti idraulici ed elettrici effettivamente esiste e non si limita alle grandezze presenti nell’esempio. La corrispondenza è mostrata nella Tabella 2:

Grandezze Idrauliche	Grandezze Elettriche
caduta di pressione	caduta di potenziale
portata	corrente
resistenza idraulica	resistenza elettrica
pompa	generatore di tensione
serbatoio	condensatore
inerzia del fluido	induttanza

Tab.2 – corrispondenze idraulico/elettriche.

Tuttavia il paragone è perfetto solo in regime laminare in cui x è legato in maniera lineare con Re ().

Lunghezza equivalente

La lunghezza equivalente è uno strumento che permette di trattare le perdite concentrate come perdite distribuite. In un generico condotto caratterizzato da L e D in cui è presente un ostacolo di coefficiente b, si può scrivere:

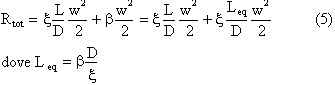
L’operazione che si compie quando si fa uso della lunghezza equivalente, è quella di riportare le accidentalità concentrate negli ostacoli in tratti di condotto liberi e di lunghezza opportuna. I valori di sono forniti da un nomogramma:

Fig.4 – nomogramma della lunghezza equivalente.

In questo tipo di grafico l’asse di sinistra riporta i vari tipi di perdite concentrate, mentre quello di destra contiene il diametro del condotto in questione. Il valore di si ottiene congiungendo i due punti e leggendo l’intersezione con l’asse centrale.

Diametro equivalente

Quando si ha a che fare con tubature di sezione non circolare le equazioni ricavate fin ora non sono più applicabili, in quanto cambia la costante di proporzionalità inversa tre numero di Reynolds e coefficiente di attrito. Per superare il problema si introduce il concetto di diametro equivalente. Esso permette di sostituire i condotti a sezione non circolare con tubi circolari di diametro pari al diametro equivalente . E’ dato da:

dove A è l’area della sezione del condotto e con perimetro bagnato si intende il perimetro che il fluido tocca all’intero del condotto. Alcuni valori di sono riportati in Tabella 3:

Sezione	Laminare	Turbolento
Circolare (diametro D)	64	D
Rettangolare (b>a)	a/b 0,1 85 0,2 76 0,5 62	1,82 b 1,67 b 1,33 b
Triangolare (lato l)	53	0,58 l
Corona circolare (altezza h)	96	2 h

Tab.3 – valori di per alcune geometrie.

Strumenti di misure fluidodinamiche

1) Metodo della pesata

E’ una misura di portata. Si applica quando si è in presenza di un flusso (in generale d’acqua) che esce da un tubo, per andare a cadere in un bacino e riprendere poi il ciclo. Infilando un contenitore nel flusso e misurando il tempo di riempimento e la massa del fluido si ottiene la misura cercata:

A discapito di quanto può sembrare è uno dei metodi più precisi. La massa infatti è misurabile con una precisione del millesimo di grammo, mentre col tempo si può scendere al centesimo di secondo.

2) Tubo di Pitot

E’ uno strumento per la misura della velocità locale di un fluido e funziona correttamente quando si opera con velocità elevate. E’ costituito da un piccolo tubo di metallo a forma di L come quello mostrato in Figura 5.

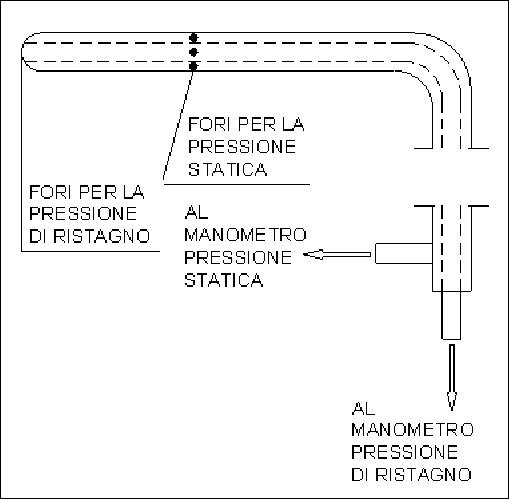
Fig. 5 – tubo di Pitot.

Il tubo è cavo ed è costituito da due tubi coassiali. Il primo comunica con l’esterno attraverso i fori per la pressione statica , mentre il secondo vi comunica tramite il foro per la pressione di ristagno . I due tubi non comunicano fra di loro. Quando il tubo di Pitot è immerso nel fluido esso si riempie di liquido e lo si orienta in maniera tale che il fluido incida sul foro nel punto di ristagno. I due valori di pressione e vengono poi misurati da manometri opportunamente collegati ai due condotti interni dello strumento. E’ importante osservare che il liquido all’interno del tubo non è in movimento ed inoltre i due valori di pressione sono diversi. Infatti entrambi saranno pari alla pressione statica , ma nel punto di ristagno si aggiunge un contributo dato dalla spinta del fluido che si blocca. Di conseguenza risulta maggiore di ed il termine di differenza è evidentemente legato alla velocità del fluido.

Se ora scriviamo l’equazione di Bernoulli, usando la velocità locale al posto di quella media perché il tubo è infinitesimo ed uguagliandola a zero per l’assenza di pompe, otteniamo:

Le perdite di carico sono trascurabili in quanto il tubo è molto corto ed è progettato per favorire uno scorrimento aerodinamico del fluido. I fori per la pressione statica sono disposti in maniera simmetrica attorno al tubo, di conseguenza il baricentro del fluido non cambia quota. E’ quindi possibile trascurare la differenza di quota . Inoltre la velocità è nulla perché nel punto di ristagno il liquido è fermo. Con queste semplificazioni l’equazione diventa:

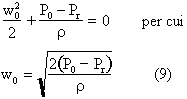
Quindi, da una misura di pressione differenziale, si può risalire alla velocità del fluido. Inoltre, spostando il tubo all’interno del flusso, e possibile fare più misurazioni e risalire al profilo di velocità.

3) Tubo di Venturi

Si tratta di un brusco convergente seguito da un dolce divergente (vedi Figura 6) ed è uno strumento per la misura della velocità.

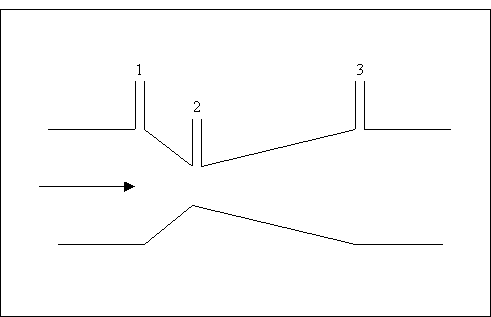
Fig. 6 – tubo di Venturi.

Il tubo di Venturi funziona solo se il fluido scorre nella direzione indicata. Se così è, posso scrivere l’equazione di Bernoulli e l’equazione di continuità e metterle a sistema:

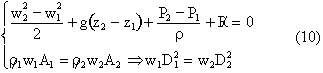
Nello scrivere il sistema si trascurano le perdite R perché siamo in un convergente e si ipotizza r costante. e sono le velocità del fluido alle rispettive sezioni, e le aree delle sezioni, e le pressioni e la differenza di quota. Supponendo il tubo orizzontale si ottiene:

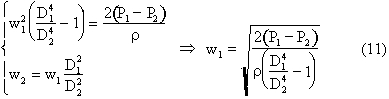
4) Diaframma

E’ uno strumento per la misura della velocità di un fluido basato sull’introduzione di un accidentalità sul percorso.

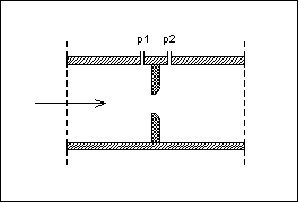
Fig. 7 – diaframma.

Tramite le aperture 1 e 2 si misurano le rispettive pressioni; dato che le velocità sono le stesse prima e dopo l’ostacolo si può scrivere:

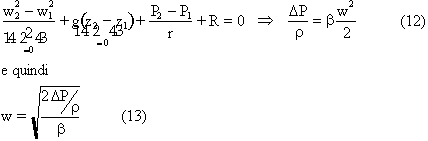
5) Rotametro

E’ un misuratore di portata di modesta precisione. E’ costituito da un tubo di vetro graduato in cui galleggia un tappo. Al passaggio del liquido quest’ultimo viene spinto verso l’alto dal flusso e sulla scala è possibile leggere il valore della portata. Si capisce come questo strumento debba essere tarato in base alla viscosità del fluido in questione, ma essa varia con la temperatura. Questo è un problema che contribuisce alla scarsa accuratezza del dispositivo.

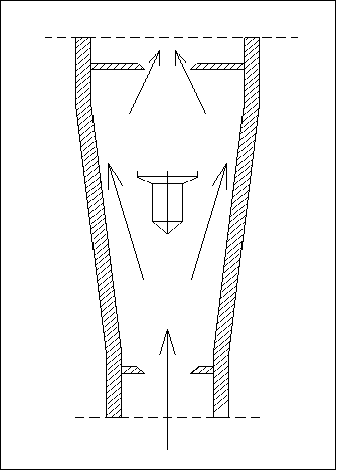
Fig. 8 – rotametro.

6) Anemometro Laser-Doppler

E’ uno strumento ottico di misura di velocità e basa il suo funzionamento su fenomeni di interferenza luminosa.

Due fasci di luce laser vengono fatti incidere e nel punto di intersezione si pone il fluido oggetto della misura. Dove i raggi di luce si incontrano si forma una zona di interferenza per cui compaiono zone di luce alternate a zone di buio. Se in questa zona scorre il fluido, le impurità contenute al suo interno saranno alternativamente illuminate ed oscurate dalle zone di interferenza. Gli impulsi ottici così generati sono catturati da un cannocchiale ed attraverso un fotomoltiplicatore, sono convertiti in un segnale elettrico visualizzabile su un oscilloscopio. E’ ora possibile ricavare la frequenza di questi impulsi che ovviamente risulta proporzionale alla velocità delle impurità (più forte esse attraversano la zona di interferenza e più impulsi vi saranno). Dalla frequenza si passa poi alla velocità, essendo la costante di proporzionalità ricavabile dalle impostazioni dello strumento.

Per riuscire a distinguere se il fluido si muove ed in quale direzione, si mantiene uno sfasamento tra i due raggi incidenti di 40 MHz. In questo modo le frange di interferenza si muovono con una frequenza di 40 MHz, e se la frequenza misurata corrisponde a questo valore significa che il fluido è fermo. Se invece si misura un valore maggiore si ha che, per effetto Doppler, la frequenza causata dalle impurità si somma a quella già presente dovuta al movimento delle frange (40 MHz) e quindi il fluido si muove in direzione concorde alle frange. Se si misura un valore minore allora il fluido procede in direzione contraria e le frequenze si sottraggono. Dalla misura della frequenza totale si risale poi alla velocità del fluido.

E’ uno strumento molto preciso ma non può essere usato con liquidi perfettamente puri (assenza di impurità) o contenuti in tubi non trasparenti alla luce laser.