RICCARDO CENTI MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 - 18.30 (PG1)

Astrazione di un problema reale

La fisica tecnica nasce dall'esigenza dell'uomo di risolvere i problemi che si presentano nel mondo reale . L'unica cosa importante in questa disciplina sono i risultati ottenuti nelle sue applicazioni in quanto ,come dice lo stesso nome ,è una scienza tecnica . Di conseguenza l'intuito e l'approccio diretto con il mondo circostante è alla base del metodo applicato in questa materia .Per questo motivo si può ritenere che le esigenze che ne hanno spinto la nascita sono antiche quasi quanto l'uomo , anche se le soluzioni ai problemi con il passare del tempo si sono evolute e notevolmente affinate .

Diffatti la fisica tecnica , come si può vedere dall'illustrazione , può far uso di numerosi strumenti che possono essere più o meno complessi e raffinati in base a quanto ci si allontana dalla realtà e si usi l'astrazione(rappresentate nella figura dalle nuvole ) . Inizialmente si cerca di risolvere intuitivamnete i problemi limitandosi al mondo reale .

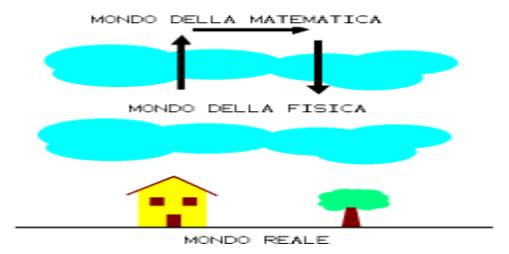
In questo caso è necessario tentare numerose volte e correggere gli errori in base

alle precedenti esperienze. Questo prende il nome di approccio diretto . Ma non sempre è possibile applicare questo metodo empirico e ottenere buoni risultati in qualsiasi situazione . Di conseguenza è necessario trovare un differente metodo di soluzione più economico in termini di numero di prove sperimentali e applicabile a qualsiasi situazione .

Occorre allora sollevarsi dal mondo reale e usare l'astrazione per entrare nel mondo della fisica e successivamente in quello della matematica che sono scienze perfette.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG2)

La fisica tecnica si può avvalere di questi potenti strumenti , oltre che all'intuito, permettendo di trovare soluzioni (magari scoperte da altri in precedenza) che non ci costringano ogni volta a ripetere la sperimentazione .

Per esempio se vogliamo sapere il tempo di discesa di un grave su un piano inclinato di cui si sanno tutte le caratteristiche (attriti , massa , momenti etc) non è necessario ripete l'esperimento ogni volta che qualche parametro cambia . Difatti sono note e reperibili in qualsiasi libro di fisica classica equazioni empiriche abbastanza accurate che descrivono modelli di questa situazione e legano il tempo di caduta con tutti gli altri attributi dell'oggetto. Ma prima di arrivare a questo punto sono occorsi alla storia centinaia di anni e il lento crearsi di percorsi mentali che hanno permesso alla fisica di nascere . Successivamente alla scoperta del metodo di indagine adeguato, le tappe obbligatorie di questo processo di evoluzione si possono riassumere in tre punti è hanno un livello di veridicità crescente :

(1) Il punto di partenza sono i principi fisici che sono alla base della fisica e che non possono essere messi in discussione .

(2) Successivamente ci sono le leggi , che nella maggior parte dei casi, essendo frutto dell'osservazione e della sperimentazione sono approssivativamente vere . Queste descrivono il comportamento degli oggetti in situazioni ideali che approssimano ciò che accade nella realtà.

(3) Infine troviamo le equazioni empiriche che sono frutto di analisi statistiche basate su situazioni reali simili fra loro e che hanno come fine legare fenomeni simili con equazioni di carattere matematico .

Partendo da questi presupposti ci è data la possibilità di astrarre ulteriormente . Usando gli strumenti offerti dalla matematica (come equazioni differenziali , grafi , analisi statistiche ,etc) e le equazioni empiriche della fisica che descrivono i singoli fenomeni ; si riesce a trovare modelli per situazioni molto complesse prima ancora di averli provati nella realtà.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 - 18.30 (PG3)

La potenzialità di questo metodo consiste nel permettere a un abile progettista di realizzare su carta (o su CAD) macchine ,potenzialmente funzionanti , senza averle mai testate in un banco di prova .

LE GRANDEZZE E IL PROBLEMA DELLA MISURA

Ma a questo punto uno si può chiedere come fare a trovare un equivalente in numeri puri delle caratteristiche che descrivono li oggetti nel mondo reale e che prendono il nome di <grandezze fisiche>. Per capire questo concetto si può iniziare dal leggere la stessa definizione.

DEFINIZIONE DI GRANDEZZA FISICA:

Si definisce grandezza fisica quella caratteristica di un ente reale o di un

fenomeno che può essere sottoposta a misura ( il cui esito sarà un numero

corredato da una corrispondente unità di misura ) e che può essere connessa

ad altre grandezze fisiche mediante opportune relazioni di carattere matematico .

Da quello che si è detto nella definizione si può capire che l'indagine fisica parte da un criterio per determinare ,tramite valore numerico ,le grandezze . Tale criterio è la misura .

Questa può essere diretta e indiretta . La prima consiste nel confronto fra la grandezza da misurare e una ad essa omogenea assunta come unità .

Un tipico esempio è la misura della lunghezza . Solitamente essa viene eseguita confrontando direttamente la lunghezza dell'oggetto in esame con un segmento di riferimento assunto come unità .

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG4)

Ovviamente questo metodo ha un limite costituito dall' esistenza o meno di un campione di riferimento (Per esempio del Newton e della temperatura non si possiede nessun campione) e dalla possibilità fisica/tecnologica di riuscire a determinare la misura come multiplo o frazione di tale campione ( estrarre la misura di volume di un oggetto partendo da un campione unitario è ben difficile).

Si definisce allora un nuovo tipo di misura , quella indiretta . Questa si usa quando la grandezza che si vuole determinare è ottenuta eseguendo la misura di altre grandezze dalle quali dipende . Uno degli esempi più semplici è costituito dal volume di un corpo di forma regolare (ad esempio un cilindro ) . In tale caso il volume viene ottenuto misurando separatamente l'altezza >h< del cilindro e il diametro >d< della sua sezione e quindi moltiplicando i valori ottenuti l'uno per l'altro secondo la relazione geometrica :

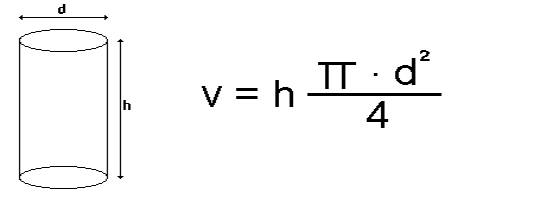
Ovviamente le unità di misure che si usano all'interno di questa formula devono essere omogenee . Altrimenti tale scrittura diventa di difficile interpretazione e in

alcuni casi priva di senso. Allora si prende un campione , si assegna a questo un valore unitario (nel nostro caso il metro) e successivamente si esprimono numericamente <h> e <d> in base a quante volte l'unità è contenuta nella grandezza da misurare . <h> e <d> vengono così espressi nel seguente modo (valori scelti a caso , non indicativi .... ) :

H = 10.3 m D = 15.5 m (m , alla fine, sta per metro)

svolgendo si ottiene che V = PI*10.3m*(15.5m/2)^2 e portando fuori le due m

V = 3.14*10.3*(15.5/2)^2 m^3 . In questa maniera abbiamo trovato per il volume una unità di misura derivata dal metro che sono i metri cubi .

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG5)

IL SISTEMA INTERNAZIONALE (SI)

Comprendendo così l' importanza del problema dell' omogeneità dell' unità di misura ed avendo ogni paese una sua tradizione in questo campo , per necessità , è nato di comune accordo uno standard chiamato SI (SISTEMA INTERNAZIONALE) senza il quale avremmo bisogno di innumerevoli tabelle di conversione come quella riportata qui sotto per la temperatura :

temperatura
	Conversioni da:	a:	moltiplicare per
	degree Celsius (°C)	kelvin (K)	T/K = t/°C +273.15
	degree Fahrenheit (°F)	kelvin (K)	T/K =  (t/°F + 459.67)/1.8
	degree Rankine (°R)	kelvin (K)	T/K = (T/°R)/1.8
	degree Celsius (°C)	kelvin (K)	1.0
	degree Fahrenheit (°F)	kelvin (K)	5.555556 E-01
	degree Rankine (°R)	kelvin (K)	5.555556 E-01

Inoltre il sistema internazionale si occupa anche di procurare un campione per ogni unità di misura fondamentale . Fino al 1960 , per esempio , la definizione di metro

era legata al prototipo internazionale platino - iridio , custodito dal 1889 nel Bureau International des Poids et des Mesures di Sèvres , presso Parigi . Nel 1960 si verificò la prima radicale innovazione che ridefiniva per mezzo della lunghezza d'onda di una radiazione monocromatica emessa , in particolari e ben definite condizioni , dall'atomo di cripto 86 . In seguito venne abbandonato anche il riferimento al comportamento atomico e la definizione di metro venne riferita al valore della velocità della luce , scelta che garantisce ora una maggiore precisione della misura e un maggior invariabilità del campione .

Campione del metro (Conferenza XVVII Generale dei Pesi e Delle Misure ottobre 1983)

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG6)

Per quanto riguarda la definizione di unità di tempo , questa fu basata , in primo tempo , sulla rotazione terrestre : un secondo corrispondeva infatti alla 86400 - esima parte del giorno solare medio . Nel 1960 la Conferenza Generale dei Pesi e delle Misure assunse una definizione che associava il secondo al moto del Sole ; precisamente il secondo corrispondeva alla frazione di 31556925,9747 dell'anno tropico , ovvero dell'intervallo di tempo che intercorre fra due passaggi consecurivi del Sole all'equinozio invernale (21 Marzo) . Come per il metro , l'esigenza di un campione più preciso indirizzò i metrologi verso un campione atomico e così la XIII Conferenza generale dei pesi e delle misure del 1967 rese ufficiale per il secondo la definizione di intervallo di tempo la cui durata è pari a quella di 9192631770 oscillazioni della radiazione emessa dall'atomo di

cesio 133 in una sua particolare transizione .

Sopra , a sinistra , un vecchio strumento per la misura del tempo : la clessidra. Il tempo necessario perché tutta la sabbia passi da una metà all'altra dello strumento attraverso il piccolo foro centrale rappresenta l'unità di tempo .A destra si può vedere una meridiana , sistema che consente la scansione del tempo mediante l'osservazione dell'ombra proiettata da un asta o da una fune opportunamente disposta e

investita dai raggi solari . Nella figura è riprodotta una meridiana del 1600.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 - 18.30 (PG7)

Per la misura della massa , il kg è l'unica unità di misura fondamentale la cui definizione è ancora legata a un campione materiale : il prototipo internazionale costruito nel 1889 e custodito nel Bureau Internation des Poid et Mesures di Sèvres .

Si tratta di un cilindro di platino - iridio , di altezza uguale al diametro della sua base ,un cilindro quindi di minima superficie totale a parità di volume .Rispetto ad esso vengono tarati per confronto , mediante bilancia , i campioni primari destinati ai paesi membri della convenzione del metro . Non si è trovato ancora un campione che permetta di esprimere l'unità di massa con miglior precisione , facendo riferimento ad un fenomeno naturale

All'italia è stato attribuito il campione numero 5 del Kg che è conservato a Roma presso l'ufficio centrale metrico del ministero dell'industria , del commercio e dell'artigianato . Un altro campione il numero 63 , è conservato a Torino presso l'istituto di metrorologia Gustavo Colonnetti , responsabile della metrologia della massa.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG8)

TABELLA DELLE DEFINZIONE DEI PESI E DELLE MISURE (SI)

Quantità	Unità		Definizione
Lunghezza (L)	Metro	M	è la distanza percorsa dalla luce nel vuoto nel tempo di 1/299792458 secondi.
Massa (M)	Kilogrammo	Kg	Il kilogrammo è l'unità di massa ed è eguale alla massa del prototipo internazionale, cilindro di platino iridio, che è conservato presso il BIPM.
Tempo (t)	Secondo	S	è l'intervallo di tempo che contiene 9192631770 periodi della radiazione corrispondente alla transizione tra i due livelli iperfini dello stato fondamentale dell'atomo di cesio 133.
Corrente elettrica (i)	Ampere	A	È l'intensità di corrente elettrica che, mantenuta costante in due conduttori paralleli, di lunghezza infinita, di sezione circolare trascurabile e posti alla distanza di un metro l'uno dall'altro, nel vuoto, produrrebbe tra i due conduttori la forza di 2x10-7 newton per ogni metro di lunghezza.
Temperatura (T)	Kelvin	K	è l'unità di temperatura termodinamica, è la frazione 1/273,16 della temperatura termodinamica del punto triplo dell'acqua.
Quantità di sostanza (m)	Mole	Mol	è la quantità di sostanza di un sistema che contiene tante entità elementari quanti sono gli atomi in 0,012 kg di carbonio 12.
Intensità luminosa (I)	Candela	Cd	è l'intensità luminosa, in una data direzione, di una sorgente che emette una radiazione monocromatica di frequenza 540 x 1012 hertz e la cui intensità energetica in quella direzione è 1/683 watt allo steradiante.

Ovviamente da queste si ricavano le altre unità di misura derivate come per esempio i Newton , in quanto sapendo che F = massa * accelerazione ottengo che il Newton corrisponde a un Kg * m(metri) / (s^2) che singolarmente sono tutte unità standard definite sopra .

LA LEGGE E LA FISICA TECNICA

Ovviamente quando un ingegnere deve realizzare un progetto, all suo interno è obbligato all'utilizzo delle unità del Sistema Internazionale ed è vincolato da alcune semplici regole che, a livello legale in Italia, sono riprese dalla normativa CNR-UNI 10003. Se ne elencano alcune.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30(PG9)

(1) I nomi delle unità sono considerati nomi comuni e pertanto si scrivono con l'iniziale minuscola , anche se alcuni di essi derivano da nomi di scienziati (ampere, kelvin) . In questo caso però sono invariabili ed hanno come simbolo una lettera maiuscola (per esempio A per l'ampere e K per il kelvin). Si noti che lo stesso vale per le unità derivate che hanno un nome proprio di persona.

(2)Il simbolo delle unità si deve usare solo quando l'unità è accompagnata dal valore numerico; esso deve essere scritto in carattere non corsivo (A e non A) dopo il valore numerico, e non deve essere seguito da un punto (a meno che si tratti del punto di fine periodo). Quando l'unità non è accompagnata dal valore numerico, deve essere scritta per esteso e non con il simbolo.

(3)Quando l'unità SI è troppo grande o troppo piccola per certe misurazioni, è consigliabile usare suoi multipli o sottomultipli. Per soddisfare le esigenze di tutti gli utilizzatori del sistema SI, il CGPM ha stabilito un certo numero di prefissi con nomi speciali, indicati nella sottostante tabella insiemi ai rispettivi fattori.

Fattore	Prefisso	Simbolo
10^24	Yotta	Y
10^21	Zetta	Z
10^18	Exa	E
10^15	Peta	P
10^12	Tera	T
10^9	Giga	G
10^6	Mega	M
10^3	Kilo	k
10^0	-	-
10^-^-3	Milli	m
10^-^-6	Micro	µ
10^-^-9	Nano	n
10^-^-12	Pico	p
10^-^-15	Femto	f
10^-^-18	Atto	a
10^-^-21	Zepto	z
10^-^-24	Yocto	y

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG10)

(4)Si raccomanda l'uso di multipli o sottomultipli che diano luogo a valori numerici compresi tra 0,1 e 1000, con il criterio di scrivere soltanto le cifre significative:

L = 10,7 ^. 10⁷ Mm.

(5) è obbligatorio utilizzare le unità di misura derivate quando possibile, quindi

non è corretto scrivere 75 kg m/s² ma bisogna scrivere 75 N.

L'ERRORE NELL'UNITà DI MISURA

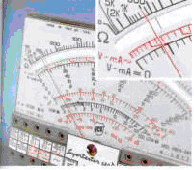
Un'ulteriore problema che coinvolge le misure e che viene regolamentato per norma di legge è l'errore che si commette nel farle . Infatti nel misurare si può aumentare l'accuratezza o la precisione usando strumenti di qualità migliore ma non si può togliere sistematicamente l'errore . Inoltre si deve fare una distinzione sul tipo di errore commesso , in quanto esistono quelli sistematici che dipendono dall'accuratezza e quelli casuali che dipendono dallla precisione.

Un errore di tipo casuale è il cosidetto errore di parallasse . Lo si commette quando si osserva l'indice in

una scala da posizioni eccessivamente angolate . Si noti nella parte situata in alto , che l'indice non si

trova sovrapposto alla sua immagine speculare prodotta dallo specchietto ad arco .

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG11)

La distinzione fra questi due termini può essere facilmente spiegata con un esempio. Prendiamo un fucile a pallini che spara contro un bersaglio . I casi possibili che si possono verificare sono in totale quattro :

Nei primi due bersagli di nota a sinistra un tiro preciso ma inaccurato , a destra un tiro sia inpreciso che inaccurato .

In questo caso , a desta , il tiro è preciso e accurato e a sinistra, è accurato ma non preciso . Quindi il tiro è tanto preciso quanto la rosa è piccola , l'accuratezza dipende invece dalla distanza del centro .Ovviamente gli stessi ragionamenti fatti sul fucile possono essere fatti per uno strumento di misura . Prendiamo come esempio un probe (sensore) usato per scopi industriali per campionare la temperatura : la pt100 . Questa è una termoresistenza realizzata usando un filo di platino la cui resistività è direttamente connessa con la temperatura del conduttore . Questo è uno strumento stabile e preciso e piuttosto accurato ma ogni tot anni questa va sottoposta a taratura altrimenti si incorre in un errore sistematico cioè la condizione in alto a sinistra.

RICCARDO CENTI - MATRICOLA 130552 LEZIONE 8 OTTOBRE 16.30 18.30 (PG12)

Ovviamente , anche l'errore , ha notevole importanza nelle tecnica e dunque quando si realizza un progetto bisogna tenere conto di questo e bisogna adottare una notazione stardard (e approvata a norma di legge) per indicarlo . Generalmente l'errore viene indicato assieme all'unità di misura che si usa per indicare la grandezza per esempio se una grandezza è espressa in metri il suo errore massimo sarà di 1 metro (in positivo o in negativo) .

L = 500 Mm (e = 1Mm)

L = 500000 Km (e = 1Km)

L = 60000000 m (e = 1m)

Quindi l'ordine dell'ultima cifra significativa mi dice che l'errore con cui è noto il valore della grandezza . Nel caso invece che l'ordine di grandezza sia moltiplicato per un esponente in base 10 alla l'errore viene espresso in base all'esponente .