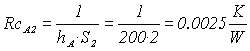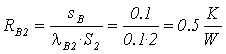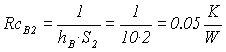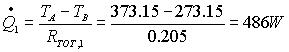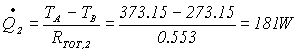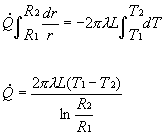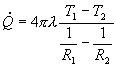UNIVERSITA’ DEGLI STUDI DI PARMA
Corso di Laurea in Ingegneria
Informatica
Corso di Fisica Tecnica
Prof. Angelo
Farina
Lezione del 4/12/2001
(ore 16:30-18:30)
Studente : Valerio
Carboni (n.m: 131268)
Sommario :
- Scambio
termico per convezione (teoria)
- Risoluzione
primo esercizio
- Risoluzione
secondo esercizio
- Determinazione
della legge di Fourier
4.1 Superficie cilindrica
4.2 Guscio sferico
- Strumenti
di misura della capacità termica
5.1 Lastra piana doppia
1. SCAMBIO TERMICO PER CONVEZIONE
Grazie alla legge di Fourier,
possiamo calcolare la dipendenza del flusso termico q (equivalente
all’energia trasmessa su unità di tempo e di superficie) dal gradiente della
temperatura, notando che questa dipendenza non è lineare Tuttavia, per
semplificare i calcoli, ci possiamo basare su una approssimazione molto
funzionale e “potente”, che prevede una proporzionalità tra q e ΔT
:
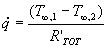
dove 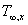 è la temperatura ad una certa distanza dalla parete (nella
figura sotto TA e TB), sufficiente perché essa sia
considerata costante, e R’TOT è la somma delle resistenze
equivalenti (figura pagina successiva) delle superfici ovvero dei condotti che
di volta in volta consideriamo.
è la temperatura ad una certa distanza dalla parete (nella
figura sotto TA e TB), sufficiente perché essa sia
considerata costante, e R’TOT è la somma delle resistenze
equivalenti (figura pagina successiva) delle superfici ovvero dei condotti che
di volta in volta consideriamo.
Possiamo riscrivere la legge in
questa forma più semplice
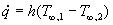
nel quale h (chiamato
coefficiente di convezione, o di irraggiamento, a seconda dei casi che andiamo
a considerare), misurato in W/m2K, è equivalente al reciproco di R’.
Per fare un esempio, dalle nostre
parti (zone poco ventilate) hESTERNO=20
W/m2K
o in una tipica stanza ferma h=8
W/m2K
2. Esercizio n.1 sulla TRASMISSIONE DEL CALORE
Si determini la
potenza necessaria in W per mantenere un locale a temperatura costante di 20°C
quando la temperatura esterna è di 0°C. Il muro divisorio tra il locale è
l’ambiente esterno è costituito di mattoni dello spessore di 25cm, ed ha una
supeficie di 10m2 .
Dati :
Superficie A=10m2
Spessore L=0.25m
Temperatura interna T1=20°C
Temperatura esterna T2=0°C
Coefficiente di conduzione λ=1W/mK
Coefficiente di convezione h1=8W/m2K
h2=20W/m2K
Risoluzione :
Il fenomeno di trasmissione del calore può essere facilmente
descritto tramite questa figura
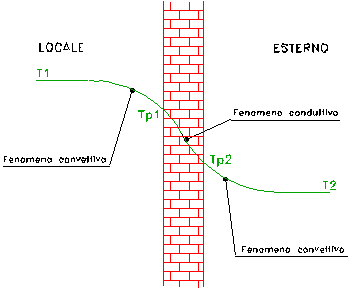
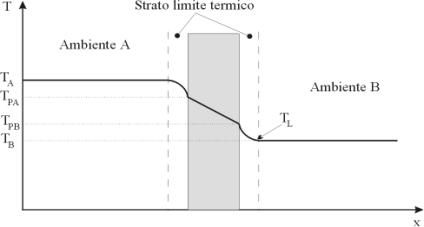
nella quale possiamo vedere che
la T1 in prossimità della parete si abbassa a causa dei moti
convettivi (la parete è più fredda perché è a contatto con l’esterno).
La medesima cosa succede nella
parete esterna, dove T2 aumenta nelle vicinanze della parete.
Le temperature di contatto Tp1
e Tp2 però non sono equivalenti, in quanto si ha un fenomeno
conduttivo all’interno della parete, dovuto al materiale, allo spessore L e
alla superfice A.
Tutto ciò può essere riassunto da questa figura
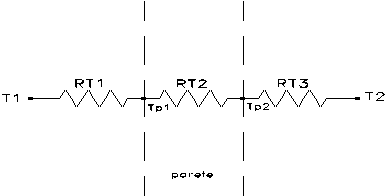
nella quale le tre resistenze sono la causa delle variazioni
di T nel nostro modello.
Da qui e dalle leggi
sopra-citate, i calcoli
R’T1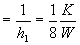 m2
m2
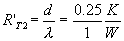 m2
m2
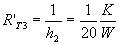 m2
m2
dove R’ e la resistenza riferita
all’unità di superficie
La resistenza equivalente della
serie è:
 m2
m2
da cui si ottiene l’energia
dispersa dalla parete per unità di tempo
:
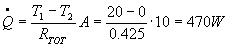
Supponiamo che la parete sia la
faccia di un cubo (escludendo il pavimento)
cioè che stiamo considerando una
stanza completamente a contatto con l’esterno :
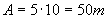 2
2
Q= 2350W
Questa è l’energia necessaria per
mantenere la stanza in temperatura costante, ma devo anche tener conto
dell’aria che si ricambia.
Quanta aria entra ed esce dalla
stanza ? Almeno ¼ del volume della stanza (minimo di legge)
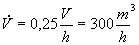 (considerando il cubo)
(considerando il cubo)
l’aria entra a 0°C ed esce a 20°C
---> il calore di ventilazione è 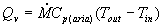
Quindi, considerando i dati 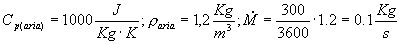
Allora Qv = 2000W
(questo per un basso ricambio d’aria, poiché abbiamo considerato il minimo di
legge, cioè che il volume d’aria scambiata sia uguale ad un quarto del volume
della stanza) che sono da sommare ai 2350W che passano attraverso le pareti
(totale = 4350W)
Per ambienti a largo affollamento
(come ad esempio un’aula) 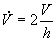 (totale = 18,35kW)
(totale = 18,35kW)
Per ambienti a medio affollamento 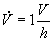 (totale=10,35kW)
(totale=10,35kW)
Da qui si può facilmente notare
che la maggior parte dell’energia serve per riscaldare l’aria, solo una piccola
parte passa attraverso le pareti.
3. Esercizio n.2
In questo caso dobbiamo
compensare la dispersione di un serbatoio contenente acqua alla temperatura di
100°C. All’esterno vi sono 0°C. La parete del contenitore è composta da una
lastra in ferro, di spessore 5cm, rivestita da una serie alterna di pannelli,
di spessore 10cm, in cemento, ma dalle caratteristiche differenti.
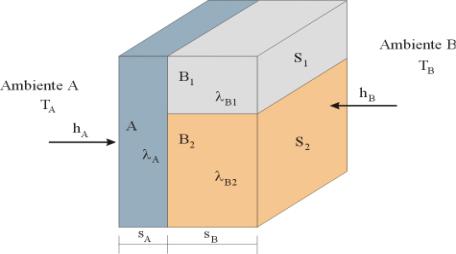
Possiamo in questo caso
analizzare una “ripetizione” singola della parete (di 3m2)
Secondo le considerazioni fatte in precedenza, possiamo
considerare la rete elettrica equivalente
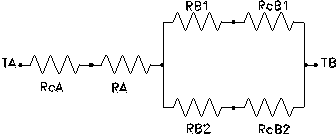
Dove considero sempre una sola
“ripetizione” nella quale A=3m2
Ma è possibile tracciare un
secondo schema nel quale possiamo “sdoppiare” la lastra di ferro (A) in due
parti distinte e congiunte, la cui sezione è pari a quella dei pannelli di
cemento a contatto :
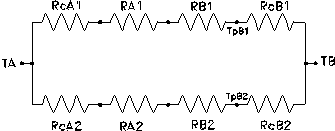
Le due figure daranno 2 risultati
differenti, poiché non c’è un risultato giusto “preciso”, come d’altra parte
non è possibile una preferenza tra i due. Si tratta solo di due approssimazioni
della realtà, pochè non teniamo conto di tante variabili (come una resistenza
tra i pannelli, o le curvature dei bordi del serbatoio).
Scelgo allora la seconda approssimazione per i miei calcoli.
Essendo Q=hS1Δt, ed RcA1=Δt/Q
Allora : 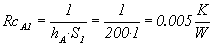
resistenza di conduzione ferro A1: 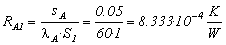
resistenza di conduzione cemento B1: 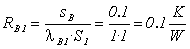
resistenza di convezione aria: 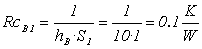
La resistenza totale del primo ramo è la somma dei singoli
contributi:
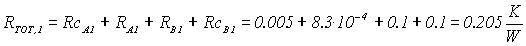
resistenza di convezione acqua : 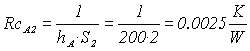
resistenza di conduzione ferro A2: 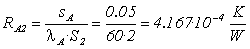
resistenza di conduzione cemento B2. 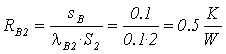
resistenza di convezione aria: 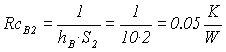
Note le temperature TA e TB è
possibile calcolare le potenze termiche dissipate dai due rami:
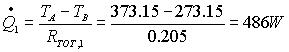
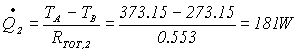
La potenza richiesta per far fronte alla dissipazione da
parte della parete del serbatoio è:
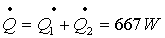
Calcoliamo, infine, le temperature di parete dei blocchi in
cemento (cioè nell’ultimo “attacco”):
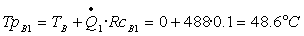
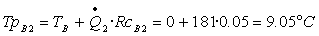
Notiamo subito che c’è molta differenza !!!
- Determinazione della legge di Fourier
4.1 Superficie cilindrica.
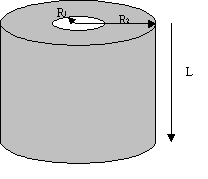
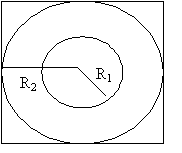
Vogliamo ora considerare un tubo
di raggio interno R1, raggio esterno R2 e lunghezza,
ponendo l’ipotesi dell’assenza della dipendenza dal tempo delle grandezze in
gioco, cioè non considerando gli eventuali transitori attuati nel processo di
nostro interesse. La figura sotto rappresenta il sistema che vogliamo studiare.
Trascuriamo, anche nel presente caso, la dipendenza del coefficiente di
conduttività termica dalla temperatura, in modo da estrarlo dal simbolo di
integrale.
Il
calcolo del flusso termico è in questo caso molto più laborioso: infatti q non
è costante su tutta la superficie del cilindro, ma esso è funzione del raggio
r:
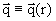
All’aumentare di r, infatti, ossia
nel caso in cui dovessimo considerare superfici più ampie, vedremmo calare
l’intensità del flusso termico: lo svolgimento dell’integrale, che in questo
caso è bidimensionale, sarebbe molto complesso. Per ricavare la soluzione della
legge di Fourier, allora, operiamo la seguente considerazione: è vero che q(r) non è costante, ma è anche vero
che il prodotto della superficie per il flusso, ossia la potenza, è costante.
Quindi possiamo scrivere:
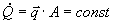
dove Q, lo ricordiamo, rappresenta la potenza termica.
E d’altra parte, poiché stiamo considerando la superficie
laterale del cilindro, possiamo calcolarla come:
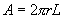
Dunque q non è invariante, ma Q lo è, sicché applicando la
definizione di potenza termica, otteniamo:
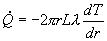
In questo caso, l’equazione differenziale è
a variabili separabili. Separando le variabili ed integrando tra il raggio R1
ed il raggio R2, otteniamo:
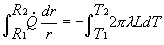
e portando fuori dal simbolo di integrale i termini costanti
(Q in particolare), si ha finalmente:
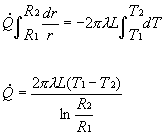
La formula ricavata consente il calcolo
della potenza termica trasmessa per conduzione attraverso la superficie
laterale di un cilindro parzialmente cavo.
4.2 Guscio sferico
Per quanto non mostrato a lezione, inseriamo
per completezza argomentativa il paragrafo che prevede il calcolo della
distribuzione del flusso di calore anche per una superficie sferica.
Consideriamo una sfera di raggio interno
R1, raggio esterno R2, di una conduttività l e
dotata di una temperatura T1 sul guscio interno e T2 su
quello esterno. Notiamo anche in questo caso che, similmente a prima, la
densità di flusso di calore non è indipendente dal raggio. Avvalendoci nuovamente
del concetto di potenza termica, integriamo l’equazione seguente:
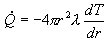
Tale equazione deriva naturalmente
dall’applicazione della definizione di potenza termica come prodotto del flusso
per la superficie di conduzione. Nella fattispecie, tale area è in questo caso
quella laterale della sfera. Considerato dunque il generico raggio r, essa è
data da:
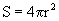
da cui si ricava l’equazione precedente. Procedendo
nell’integrazione, notiamo che l’equazione differenziale è a variabili
separabili e pertanto può essere integrata direttamente mediante i seguenti
passaggi algebrici:
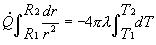 , da cui à
, da cui à 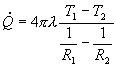
5. Strumenti di misura della conducibilità
termica
Per calcolare la trasmissione del calore in laboratorio si
usano essenzialmente due dispositivi: la lastra termica doppia e il termoflussimetro.
Il primo è il più raffinato e preciso e viene utilizzato prevalentemente in
laboratorio (costa parecchie migliaia di euro), il secondo, meno preciso, si
utilizza sia in laboratorio che in opera (dal costo di poche centinaia di euro)
5.1 Lastra termica doppia
Questo strumento presenta una struttura costituita da due bagni
termostatici e da un riscaldatore elettrico centrale.
Solitamente un riscaldatore elettrico consiste in una lastra
di materiale al cui interno è presente una resistenza elettrica.
La lastra è circondata da un anello di guardia
(figura sotto) che porta le dimensioni complessive a 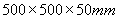 e che serve per
trascurare gli effetti sul bordo
e che serve per
trascurare gli effetti sul bordo
In questo modo è possibile sapere con esattezza la
potenza termica che si sta erogando.
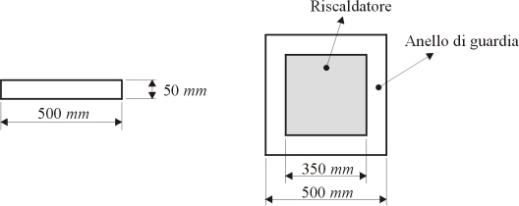
Il blocco formato da elemento riscaldatore di tipo elettrico
e anello di guardia viene montato poi fra due strati del materiale di cui si
vuole misurare la conducibilità termica, e a sua volta si pone il sistema così
ottenuto fra due bagni termostatici atti a imporre una temperatura di parete
costante T0 (figura sotto)
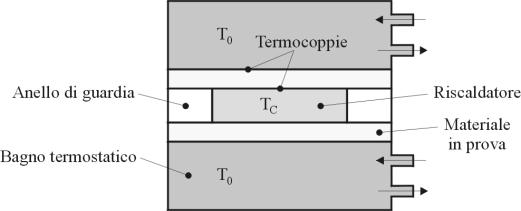
Lo strumento è dotato di misuratori di temperatura che
consistono in termocoppie collocate sulle pareti del materiale in prova.
Si misura quindi la temperatura T0 del bagno termostatico e
la temperatura TC dell’elemento riscaldante.
Si conosce dunque la potenza termica la quale, considerando
una superficie S e uno spessore s, è inoltre data dalla
relazione:
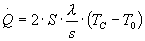
Nell’equazione compare come unica incognita la conducibilità
l del materiale, che si può
quindi facilmente ricavare.
5.2 Termoflussimetro
Il termoflussimetro è uno strumento utilizzato
prevalentemente nei casi in cui non è
richiesta un’elevata precisione. La sua conformazione è molto simile a quella
della lastra termica doppia tranne per il fatto che non sono presenti
riscaldatore elettrico e anello di guardia.
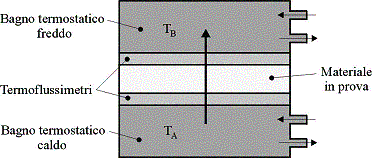
La misura della conducibilità si effettua ponendo
una piastra di materiale in prova fra due bagni termostatici a due temperature
diverse T1 e T2 , solitamente in modo da
far fluire il calore dal basso verso l’alto.
Per poter calcolare la quantità di calore scambiato
si inseriscono, fra i bagni termostatici e il materiale in prova, due sottili
lastre di materiale con conducibilità termica nota (di solito gomma), le quali
prendono appunto il nome di termoflussimetri e hanno solitamente
dimensioni normalizzate a 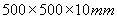 .
.
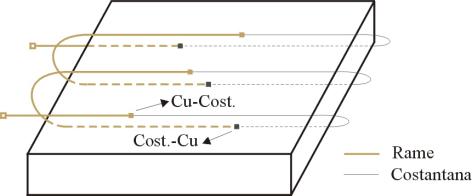
Ciascun termoflussimetro è dotato di una termocoppia
differenziale, la quale è costituita da un avvolgimento di fili di due
materiali diversi, ad esempio rame e costantana. I fili vengono avvolti attorno
al termoflussimetro in modo da avere tante giunzioni distribuite sulla
superficie della lastra ma mantenendo sempre le giunzioni rame-costantana sulla
parte superiore e le giunzioni costantana-rame su quella inferiore In questo
caso non si utilizza il giunto freddo, ma si misura direttamente la differenza
di potenziale ai due capi di rame con un voltmetro.
La tensione misurata dal voltmetro non è
proporzionale alla temperatura del termoflussimetro, bensì è direttamente
proporzionale alla differenza di temperatura fra le due superfici dello stesso,
cioè è proporzionale al flusso termico.
Perciò, con un adeguato fattore di scala sullo
strumento, è possibile leggere direttamente il flusso termico dal segnale
elettrico. Si hanno due valori di flusso, uno per ogni termoflussimetro, i
quali vengono mediati in modo da considerare sia il valore entrante che quello
uscente.
In un sistema di questo tipo si ha inoltre che:
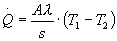
Risulta perciò possibile ricavare
dall’equazione la conducibilità termica
del materiale in prova.
In questo dispositivo sono però presenti effetti di
bordo, ad esempio è da tenere in considerazione la resistenza termica del
termoflussimetro stesso, la quale non deve alterare significativamente la
resistenza termica complessiva del materiale in esame.
L’uso della termocoppia differenziale consente di
avere un segnale elettrico molto forte anche con piccole differenze di
temperatura, in quanto le forze elettromotrici delle giunzioni, che sono in
serie, si sommano.
Il termoflussimetro, anche se poco preciso, risulta quindi
essere uno strumento di misura economico e funzionale anche per applicazioni di
tipo ingegneristico.
![]()
![]() è la temperatura ad una certa distanza dalla parete (nella
figura sotto TA e TB), sufficiente perché essa sia
considerata costante, e R’TOT è la somma delle resistenze
equivalenti (figura pagina successiva) delle superfici ovvero dei condotti che
di volta in volta consideriamo.
è la temperatura ad una certa distanza dalla parete (nella
figura sotto TA e TB), sufficiente perché essa sia
considerata costante, e R’TOT è la somma delle resistenze
equivalenti (figura pagina successiva) delle superfici ovvero dei condotti che
di volta in volta consideriamo.![]()



![]() m2
m2![]() m2
m2![]() m2
m2![]() m2
m2![]()
![]() 2
2![]() (considerando il cubo)
(considerando il cubo)![]()
![]()
![]() (totale = 18,35kW)
(totale = 18,35kW)![]() (totale=10,35kW)
(totale=10,35kW)