ANALISI DI SUONI COMPLESSI
Lo scopo dell’analisi
in frequenza è quello di definire il contenuto di un suono complesso, che
contiene componenti a diverse frequenze, anche variabili istantaneamente.
Ricordando che il campo sonoro udibile umano va
circa dai 20 Ha ai 20 kHz e che l’orecchio non percepisce tutte le frequenze
allo stesso modo, si capisce come mai in molte applicazioni tecniche che vanno
dalla registrazione e riproduzione della musica all’analisi del rumore prodotto
da macchinari o ambienti, si è interessati a valutare non tanto il livello
sonoro complessivo, cioè l’energia totale del suono, bensì la sua distribuzione
alle varie frequenze.
In natura non esistono però solo suoni puri (le
sinusoidi utilizzate in teoria e molto comode per un’analisi matematica sono
molto lontane dalla realtà); sono presenti forme d’onda molto strane (ad
esempio dall’analisi della voce umana si nota che essa non ha nulla a che fare
con una semplice sinusoide). Anche il suono prodotto da uno strumento musicale
(una ben precisa nota) non è fatto unicamente di sinusoidi.
In un suono reale sono quindi sempre presenti
sinusoidi discrete con opportune ampiezze, frequenze e fasi alle quali è
sovrapposta una quota di rumore.
Effettuare l’analisi in frequenza significa partire
da una rappresentazione del suono nel dominio del tempo, cioè dalla forma d’onda, ed arrivare a definire lo spettro (un procedimento analogo è fatto
nell’ottica dove la luce è scomposta nelle sue componenti cromatiche,
nient’altro che onde a diversa frequenza).
In sostanza, un suono puro è un’ onda sonora la cui pressione acustica
istantanea è una semplice funzione
sinusoidale del tempo, esprimibile quindi mediante una relazione lineare del tipo :
In pratica, i suoni puri
permanenti sono un’ eccezione : normalmente, infatti, il fenomeno sonoro si
presenta come suono complesso costituito da un insieme discreto o
continuo di oscillazioni sinusoidali. Se la funzione DP(t) che rappresenta il fenomeno sonoro è
periodica, essa è analizzabile in serie di fourier in quanto un’oscillazione
periodica complessa può essere considerata come una somma di una serie di
oscillazioni sinusoidali semplici, le cui frequenze costituiscono una
progressione aritmetica.
Cioè, se considero un
segnale x(t) periodico di periodo T e frequenza f = 1/T, lo posso
sviluppare come somma di infiniti termini armonicamente correlati, ciascuno dei quali è caratterizzato da una
frequenza multipla della frequenza f (frequenza fondamentale) . In
formule risulta che
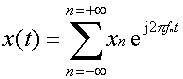
dove i coefficienti dello
sviluppo sono
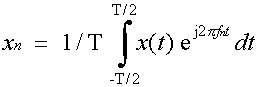
La frequenza f1, più
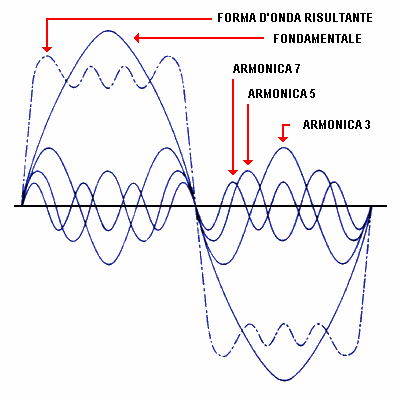
bassa, viene chiamata frequenza fondamentale, mentre le altre
componenti, di frequenze f2=2f1, f3=3f1...,sono dette armoniche (va tenuto presente
che la prima armonica è la fondamentale, la seconda armonica la f2, e così via).
Sono di questo tipo i suoni emessi dagli strumenti musicali.
Oltre alle frequenze
multiple della stessa fondamentale, un suono può risultare costituito anche da
frequenze che stanno ancora in rapporto semplice, ma non intero, con la più
bassa ; queste frequenze sono chiamate parziali e rivestono un ruolo
importante in acustica musicale, ad esempio negli strumenti a percussione.
Armoniche e parziali caratterizzano il timbro del suono. Possono
presentarsi anche casi in cui il suono complesso è costituito da una serie di
frequenze pure che stanno tra loro in relazione non armonica. Cio accade, ad
esempio, quando quando si eccitano contemporaneamente più modi propri di di oscillazione di corpi vibranti, quali le
membrane tese o le piastre, che possiedono appunto frequenze proprie di
risonanza in relazione non armonica.
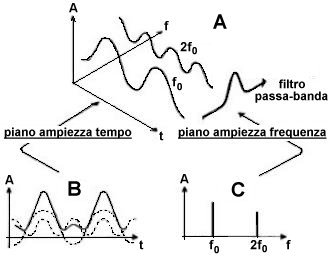
In ogni caso, i suoni
complessi sopra definiti possono essere rappresentati mediante un certo numero
(teoricamente infinito!) di termini sinusoidali semplici i quali, come è noto,
restano individuati ciascuno dai parametri A, f, φ, ossia dall’ ampiezza
massima di oscillazione, dalla frequenza e dalla fase. La conoscenza di tali
grandezze permette quindi di ricostruire l’ oscillazione complessa.
Potendosi trascurare,
agli effetti dell’ ascolto, la fase in quanto l’ orecchio avverte
principalmente le differenze di ampiezza e frequenza di oscillazione, il suono
complesso poò essere rappresentato graficamente da una successione di righe,
ciascuna delle quali individua con la sua ascissa la frequenza e con la sua
ordinata l’ intensità.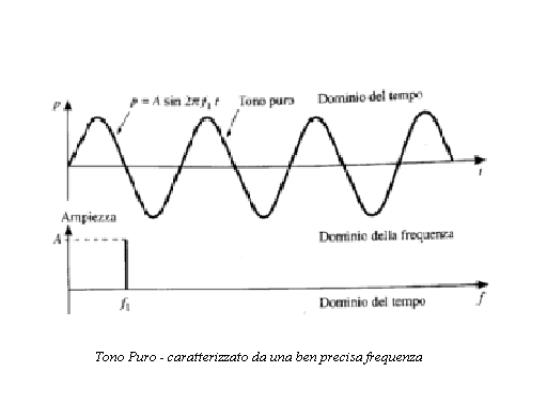
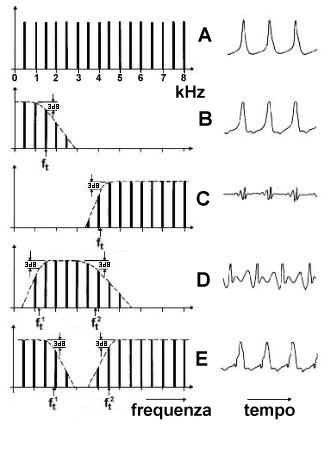
Se, invece, il suono periodico non è puro, ma è complesso, allora la situazione in frequenza è quella della figura seguente :
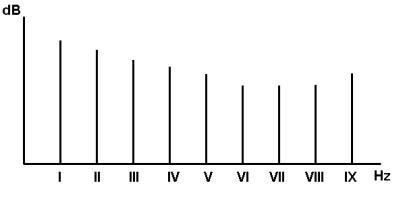
Normalmente, si usa prendere come grandezza
rappresentativa dell’ intensità il valore efficace P della pressione
acustica, definita come :
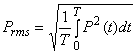
dove 
non è altro che la pressione istantanea al
quadrato.
Il valore efficace (RMS)
è quello che rappresenta meglio il contenuto energetico dell'onda.
L’ insieme di righe del
grafico prende il nome di spettro acustico, o diagramma di analisi
armonica.
Il valore efficace dell’ oscillazione armonica nel suo insieme è dato dalla relazione :
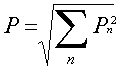
essendo Pn il valore
efficace dell’ ennesima armonica.
Nella maggior parte dei
casi pratici, la funzione ΔP(t) che definisce la pressione sonora in un
punto, non è analizzabile in serie di frequenze pure, ma e una funzione
aleatoria che presenta uno spettro continuo in frequenza. E’ questo il caso di
un gran numero di rumori quali, ad esempio, il rumore termico di
apparecchiature elettroniche, il rumore generato da aviogetti, ecc.
Infine esistono fenomeni
acustici (musica, linguaggio parlato, ecc.) costituiti da un gran numero di
suoni di breve durata che si susseguono in rapida successione; ciascuno di tali
suoni risulta in genere caratterizzato da un transitorio di attacco e un
transitorio di estinzione, durante i quali l’ ampiezza della perturbzaione di
pressione cresce sino ad un valore di regime e, rispettivamente, decresce fino
ad annullarsi.
Anche questi tipi di
fenomeni acustici possono essere convenientemente rappresentati da un diagramma
spettrale, purchè si tenga conto della variazione temporale delle grandezze
acustiche che li caratterizzano.
SPETTRO SONORO : FILTRAGGIO
|
Lo spettro di un segnale (e quindi la forma stessa del
segnale) può essere modificato se sottoposto ad un’operazione di filtraggio.
Un filtro è appunto un dispositivo che opera una trasformazione sulla
struttura spettrale di un segnale, trasmettendone una parte ed eliminandone
le parti restanti. In altre parole un filtro ha la proprietà di agire,
modificandola, sulla ampiezza delle componenti, lasciando inalterata la loro
frequenza. Consideriamo ad esempio un segnale periodico le cui armoniche
abbiano tutte la stessa ampiezza, cioè le cui righe spettrali siano tutte
della stessa altezza (A).
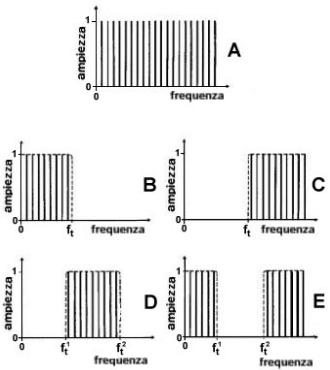
Esistono quattro modalità tipiche di trasformarlo con un’operazione di
filtraggio. Se il filtro trasmette solo le armoniche aventi frequenza
inferiore alla cosiddetta frequenza di taglio
(ft), si parla di filtraggio passa-basso (B); si parla invece di filtraggio passa-alto (C) quando sono trasmesse solo le armoniche
di frequenza superiore a quella di taglio. Quando le armoniche trasmesse sono
quelle di frequenza compresa fra due frequenze di taglio si parla di
filtraggio passa-banda
(D); mentre se le armoniche
comprese fra due frequenze di taglio vengono eliminate si tratta di un
filtraggio elimina-banda
(E). |
|
|
|
|
|
|
|
|
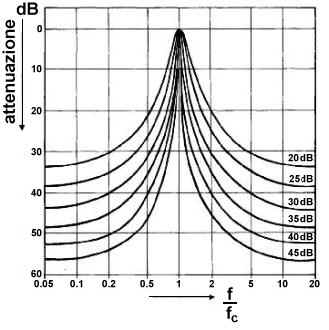
Le trasformazioni spettrali descritte sono realizzate
da filtri ideali; per esempio un filtro passa basso ideale, come si è visto,
trasmette senza attenuazione tutte le frequenze inferiori a ft,
ed elimina completamente tutte quelle superiori. In realtà non esistono
filtri ideali: ogni filtro «reale» inizia ad attenuare (leggermente) in
prossimità della frequenza di taglio e dopo di questa opera una attenuazione
progressiva (più o meno marcata) e non una drastica eliminazione. Nel caso
dei filtri reali, la frequenza di taglio ft, è
definita come la frequenza a cui il filtro attenua di 3 dB il livello di
ampiezza massimo. Inoltre il tasso di attenuazione oltre la frequenza di
taglio viene chiamata pendenza
e si misura in dB per ottava (dB/oct).
Quanto più la pendenza di un filtro (reale) è grande, tanto più esso si
avvicina al corrispondente filtro ideale. Nel caso di un filtro passa-banda,
in alternativa alle due frequenze di taglio è più usato il parametro larghezza di banda, o banda passante, definito come la
differenza fra le frequenze di taglio stesse. |
|
|
|
|
|
|
|
|
Inoltre, nel caso di un filtro passa-banda simmetrico
un ulteriore suo parametro caratteristico è la frequenza centrale (fc), definita come la media
delle due frequenze di taglio. Spesso nei passa-banda simmetrici la
«simmetria» non è definita su una scala lineare di frequenza, bensì su una
scala logaritmica del «valore percentuale» di frequenza. |
|
|
|
|
|
|
|
|
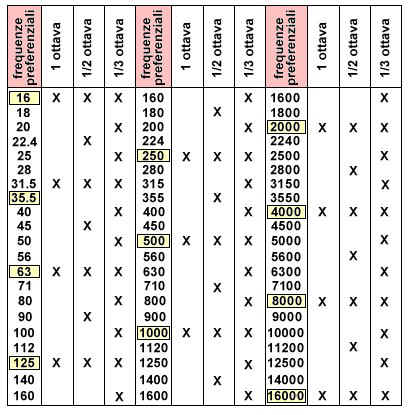
La tabella illustra i «valori preferenziali» di
frequenza (centrale) utilizzati negli analizzatori, rispettivamente, «di
ottava», di «1/2 ottava». di «1/3 d’ottava».Questa serie di frequenze è
intesa per misure acustiche e non concerne il campo musicale. Come base di
tutte e tre le serie di frequenze preferenziali è stata scelta (come è
tradizione in acustica) la frequenza di 1000 Hz. Si noti che in queste serie
di valori di frequenza si utilizza un «incremento percentuale» costante e non
un «incremento assoluto» costante. Per esempio, nella scala «di ottava», un
dato valore di frequenza è pari al 200% del valore precedente, cioè
l’incremento (percentuale costante) è del 100% e ad esso corrispondono
incrementi assoluti (in Hz) crescenti col crescere della frequenza. |
|
|
|
|
|
|
|
|
L’altra tecnica fa ricorso ad un singolo filtro
passa-banda di cui viene fatta variare nel tempo la frequenza centrale: in
tal modo il filtro compie una «esplorazione» della scala di frequenza e
misura in successione l’ampiezza (e la frequenza) di ciascuna armonica. In
questo caso l’analisi avviene in tempo
differito, cioè intercorre un certo ritardo fra
l’immissione del segnale e la definizione completa del suo spettro. E’
importante, perché il filtro passa-banda estragga ciascuna armonica
singolarmente, che la sua larghezza di banda sia inferiore all’intervallo di
frequenza che separa due armoniche adiacenti; in altre parole la larghezza di
banda deve essere inferiore alla frequenza del segnale complesso periodico da
analizzare. In tal caso si dice che il filtro è a banda stretta. Di contro si parla di
filtri a banda larga,
quando la loro larghezza di banda è maggiore della frequenza del segnale, per
cui essi misurano nello stesso tempo due o più armoniche del segnale. In
questo caso, si ottiene un risultato (spettrale) che è ancora largamente
utilizzabile in Fonetica. |
|
|
|
TIPI DI
RAPPRSENTAZIONE DELLO SPETTRO
Uno
spettro, a seconda della tecnica utilizzata per ricavarlo e del tipo di
visualizzazione impiegata, può cambiare notevolmente d’aspetto. Esiste,
infatti, una prima differenza tra l’analisi in banda stretta e in banda
percentuale costante, ed una seconda differenza nella rappresentazione con asse
delle frequenze lineare e logaritmica.
Prendiamo,
di seguito, in esame lo spettro di uno stesso segnale, analizzato con lo stesso
strumento e rappresentato in quattro differenti modi.
1. Analisi
per bande percentuali costanti in terzi d’ottava con asse delle frequenze in
scala logaritmica (fig. 1) (i terzi presentano tutti la stessa larghezza).
Graficamente notiamo un segnale piuttosto livellato con un picco alla frequenza
di circa 2000 Hz.
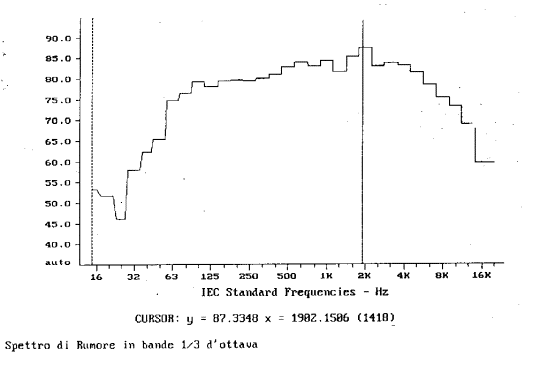
Fig.1
2.
Analisi per bande
percentuali costanti in terzi d’ottava con asse delle frequenze in scala
lineare (fig. 2) (aumentando la frequenza i terzi si allargano). Dallo spettro
si nota un segnale che presenta un picco a frequenza apparentemente bassa e che
va diminuendo di livello salendo ad alta frequenza.
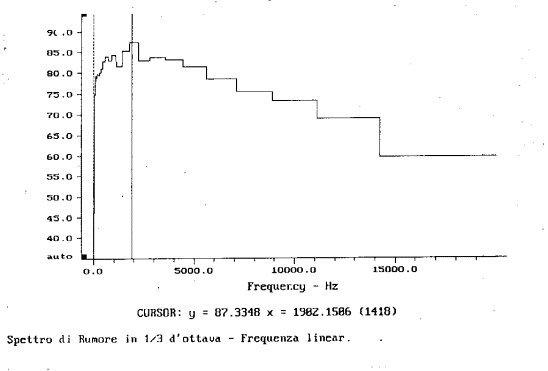
Fig. 2
Apparentemente i due spettri sono molto differenti, ma in realtà rappresentano sempre lo stesso segnale: si può vedere questo osservando il valore indicato dal cursore. In entrambi i casi si ha un picco di 87,3 dB alla frequenza di 1982,1286 Hz.
Passiamo ora dai filtri a banda percentuale costante a quelli a banda costante.
3. Analisi in banda stretta con asse delle frequenze logaritmica (fig. 3).
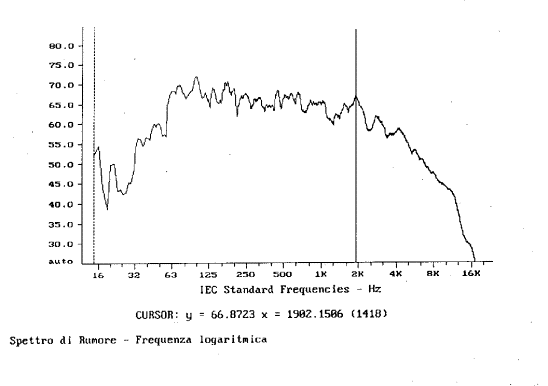
Fig.
3
4. Analisi in banda stretta con asse delle frequenze lineare (fig. 4).
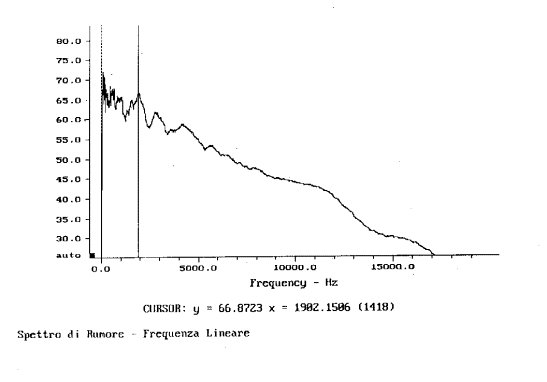
Fig. 4
Negli ultimi due casi, essendo le bande più
strette, esse riescono a catturare frequenze ad un’energia mediamente inferiore
a quella catturata dalla banda in terzi d’ottava. Normalmente, rispetto
all’andamento in terzi d’ottava, un segnale visualizzato in banda stretta,
tenderà ad attenuare i livelli ad alta frequenza ed ad incrementare quelli a
bassa frequenza. Questo si può notare sia dalla fig. 18 sia dalla fig. 19.
Infine passando dall’analisi in terzi d’ottava
alla banda stretta il valore in dB del segnale varia. Notiamo che a 2 kHz nei
primi due grafici si otteneva un picco a 87,13 dB mentre negli ultimi due esso
valeva 66,87 dB (circa 20 decibel di differenza).
Possiamo concludere con certezza che è
necessario stabilire il tipo d’analisi in frequenza in quanto la scala
tipografica della rappresentazione dello spettro ne può alterare notevolmente
la lettura.
Resta comunque da sottolineare che il nostro udito
è meglio rappresentato dall’analisi in terzi d’ottava con asse delle frequenze
in scala logaritmica.
INTENSITA’ ACUSTICA
Un
altra grandezza che è interessante calcolare per valutare il fenomeno del
trasporto di energia dell’onda piana progressiva è l’intensità acustica che
rappresenta il valore medio nel tempo dell’intensità istantanea Ii(t)
(19)
da
cui l’intensità media
(20)
Dopo
aver riscritto le equazioni della velocità e della pressione in funzione
dell’impedenza:
(21)
(22)
posso calcolare l’intensità media (ricordando la
formula trigonometrica :
(23)
la quale vale ½ se integrata mediamente nel tempo
) ottenendo tre possibili risultati:
(24)
(25)
(26)
Se
poi si utilizzano le espressioni dei valori medi efficaci ,in quanto si parla
di grandezze sinusoidali, 
e 
(l’acronimo rms sta per Root Mean Square):
(27)
(28)
l’intensità può essere riscritta come:
(29)
(30)
(31)
In
generale c’è la tendenza ad abusare di queste formule per la loro estrema
comodità di calcolo e semplicità,soprattutto per quanto riguarda la
(30).Infatti fino agli anni Ottanta questa espressione era usata per calcolare
l’intensità di qualsiasi forma d’onda,commettendo un grossolano errore dal
momento che recentemente si è appurato che vale solo per l’onda piana
progressiva!Ciò che aveva tratto in inganno era il significato fisico di
equivalente energetico del valor medio efficace.Si indicava con esso ,sbagliando, l’energia immagazzinata dal
sistema invece di far riferimento solo all’energia potenziale.Avendo calcolato
solo il valor medio efficace della pressione in un campo acustico generico,non
si è in grado di valutare l’energia cinetica in quanto non è detto che tutta
l’energia potenziale si trasformi in energia cinetica!Anzi solitamente
l’energia immagazzinata come energia potenziale è mediamente maggiore
dell’energia cinetica e viceversa ci sono casi in cui è vero il contrario ,cioè
che l’energia immagazzinata in termini di velocità,e quindi l’energia cinetica,
è superiore all’energia potenziale.Solo per l’onda piana progressiva sussiste
la seguente uguaglianza:
(32)
e dall’uguaglianza dell’intensità si scrive:
(33)
Quindi nell’apprestarsi allo studio di un onda qualsiasi non è
sufficiente conoscere solo la pressione per valutare l’intensità,occorrono
pressione e velocità. L’unico termine che rimane sempre valido è l’intensità
valutata come media integrale nel tempo.
MISURE
FONOMETRICHE
Le misure fonometriche ci permettono di analizzare
e quantificare il suono.
Ogni
giorno siamo investiti da onde sonore rumori, voci, musica e talvolta può
essere utile poterli misurare: in ambienti di lavoro, di studio, strade ecc.
allo scopo di rilevare il livello di inquinamento acustico.
Per
effettuare tali misure si utilizza il fonometro.
Si
possono trovare in commercio diversi tipi di fonometro con diverse prestazioni
e diverse caratteristiche.
Lo strumento, grazie al microfono di cui è dotato, è in grado di rilevare le variazioni di pressione generate dalle onde sonore e di visualizzare successivamente su un display (eventualmente su un elaboratore elettronico) il livello di campo misurato.
Oggigiorno i fonometri sono anche in grado di effettuare l’analisi in frequenza del segnale captato.
Fig.1)
Partendo da sinistra: microfono, fonometro, generatore di tono puro (indispensabile alla calibrazione del
fonometro), cuffietta di
protezione anti-vento.
Prima di descrivere il funzionamento del fonometro avvalendomi dello schema a blocchi, devo effettuare alcune importanti premesse.
Grandezze misurate e definizione di Livello
Equivalente (LEQ)
Il fonometro è in grado di misurare i livelli di pressione, esso campiona il segnale in ingresso ad intervalli di tempo ben definiti che possono variare a seconda della costante di tempo (τ = RC) scelta dall’utente; esistono tre tipi di costanti di tempo:
|
τ |
Periodo “ T “ (ms) |
N° di campioni al sec. |
|
SLOW |
1000 |
1 |
|
FAST |
125 |
8 |
|
IMPULSE |
35 |
28 |
Una volta scelta la costante di tempo desiderata, il fonometro rileva nell’unità di tempo i livelli di pressione (LP) istantanei. (Es: 8 rilevazioni al secondo nel caso di costante FAST ).
Matematicamente il livello di pressione (Lp) è definito da:
dove:
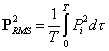
PRMS rappresenta il valore medio efficace.
Pi = Pressione istantanea del campo sonoro.
P0 = Pressione di riferimento, circa 2x10-5 (Pa)
Possiamo dare, a questo punto ,la definizione matematica di livello equivalente (LEQ)
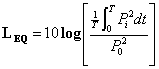
Per calcolare “fisicamente” il LEQ possiamo avvalerci di un semplice circuito elettronico (RC) che, utilizzato come rivelatore del valore medio efficace, fornisce una risposta di questo tipo:
CIRCUITO RC :
SCHEMA A BLOCCHI:
SCHEMA ELETTRICO:
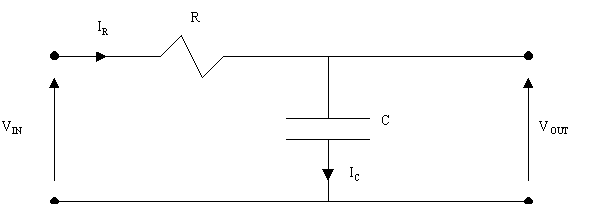
Supponiamo di applicare in ingresso un segnale delta-di-Dirac ( δ(t) ) allo scopo di trovare la risposta impulsiva ( h(t) ) del filtro.
La funzione di trasferimento del filtro sarà quindi:
ma:
imposto quindi l’equazione differenziale:
risolvo l’equazione applicando il metodo della variazione delle costanti:
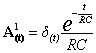
integrando ambedue i membri…
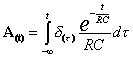
quindi:
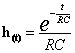
a questo punto posso sfruttare h(t)
per trovare il generico segnale di uscita (Vout);
l’elevamento al quadrato deriva dal fatto che mi interessa il valore medio
efficace.
il segnale di uscita Vout è quindi ottenuto dalla convoluzione tra Vin e h(t) :
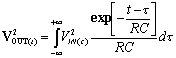
(t – τ < 0 ) è h(t) = 0 quindi il segnale di uscita sarà:
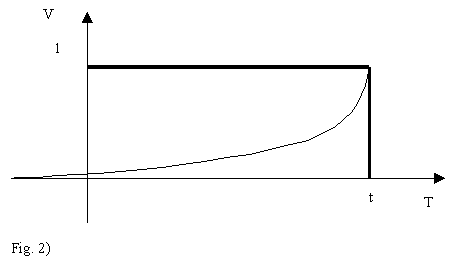
Il termine esponenziale, presente all’interno dell’integrale, rappresenta una “memoria” in funzione del tempo; dal grafico riportato qui sotto (Fig.2) si nota l’andamento ideale (rappresentato con un tratto di linea più spesso) e l’esponenziale negativo, che rappresenta la memoria presente nei fonometri analogici:
Oss. L’esponenziale decresce infinitamente, ma dopo un tempo pari a 5τ non influenza più il nostro sistema.
FORMULA
PRATICA PER DETERMINARE LEQ
Il livello
equivalente è una media energetica: cioè una media dei valori di intensità del
segnale campionato, non di livello.
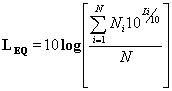
Li = Livello
campionato (dB)
Ni= numero di
campioni rilevati per il livello Li
Il calcolo del livello
equivalente (LEQ) può essere fatto direttamente dal fonometro oppure
i dati del segnale campionato possono essere elaborati per esempio da un foglio
di lavoro .
Per la misura di Leq è necessario effettuare il campionamento
dell’andamento temporale. Questo
stesso campionamento ha un'ulteriore rilevanza, dovuta al decreto misure del
marzo '98, il quale afferma che sul suono misurato possono essere effettuate
tre possibili correzioni:
1)
C1 (per componente impulsiva)
2)
C2 (per componente tonale)
3)
C3 (per componente tonale a bassa frequenza)
Per ogni correzione di
questo tipo vengono addizionati 3 dB e il livello del rumore ambientale (LAMB) è dato
dalla somma :
LAMB = Leq + C1 + C2 + C3
E' necessario, allora,
stabilire secondo il decreto misure del marzo '98 che cosa si intenda per
rumore impulsivo. Il decreto afferma che:
"Il rumore è considerato avente componenti
impulsive quando sono verificate le condizioni seguenti:
·
l’evento è ripetitivo;
·
la differenza tra LAImax ed LASmax è superiore a 6 dB;
·
la durata dell’evento a -10 dB dal valore LAFmax è
inferiore a 1 s."
La prima condizione è
chiarita nel decreto qualche riga più avanti.
"L’evento sonoro impulsivo si considera
ripetitivo quando si verifica almeno 10 volte nell’arco di un’ora nel periodo
diurno ed almeno 2 volte nell’arco di un’ora nel periodo notturno."
Passiamo quindi al
secondo punto. LAImax, e LASmax rappresentano rispettivamente il massimo livello
misurato secondo la metodologia IMPULSE e secondo la metodologia SLOW. Allora
per avere un rumore impulsivo deve valere la condizione:
LAImax - LASmax > 6 dB
La formula precedente, tuttavia, è soddisfatta anche dalla voce umana (il che significa che è una condizione debole, perché facilmente verificabile). Per questo motivo è stata introdotta la terza condizione, dove compare il termine LAFmax che indica il massimo livello misurato con la costante di tempo FAST. La terza condizione può essere schematizzata dal seguente grafico (Fig. 3).
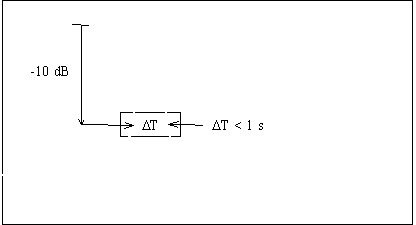
Fig.
3)
Data la traccia FAST del
segnale, deve essere verificato che, abbassandosi di 10 dB rispetto al valore
massimo, la durata dell'impulso sia minore di un secondo. Si vede così che è
necessario misurare contemporaneamente l’andamento temporale con le tre costanti di tempo IMPULSE, FAST e SLOW.
Tuttavia l'unico strumento che permette direttamente una misura di questo tipo
è il fonometro della Larson Davis ed è molto costoso. La maggior parte dei fonometri
invece permette una misurazione per volta. Quindi l'unica soluzione è quella di
registrare il segnale e poi inserirlo nuovamente nel fonometro in metodologia
IMPULSE, FAST e SLOW.
Devo però fare attenzione a registrare il segnale in modo da non perdere nessuna informazione e da non introdurre nessun disturbo. Un modo corretto è quello di registrarlo su disco fisso nel computer o su un sistema di registrazione "senza perdite". Infatti se decidessi di fare la registrazione ad esempio su un CD, perderemmo molte delle informazioni necessarie, proprio perché il CD utilizza algoritmi di compressione che perdono parte del segnale.
ESEMPIO:
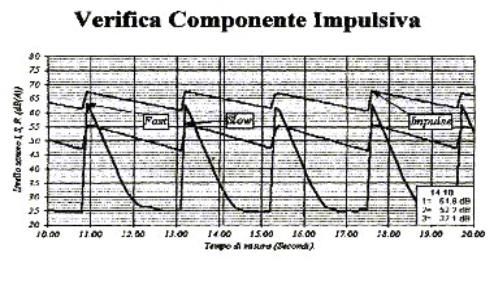
Fig. 4) Osservando il grafico, che riporta un segnale campionato con costanti SLOW, FAST, IMPULSE; notiamo che siamo in un classico caso di applicazione della penalizzazione.
FONOMETRO:
SCHEMA A BLOCCHI:
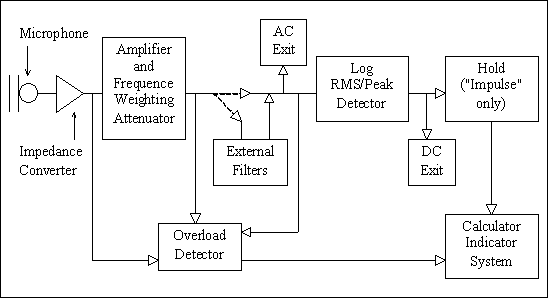
DESCRIZIONE DEI SINGOLI BLOCCHI:
MICROFONO (MICROPHONE): Il microfono è il
trasduttore pressione - tensione che
permette di rilevare le variazioni del campo sonoro. Contenuto in una struttura
tubolare è sensibile unicamente alla pressione, e non alla velocità del campo.
E’ quindi totalmente privo dell’effetto “ prossimità
“ (per il quale si avrebbe una sovramplificazione delle basse frequenze).
La caratteristica
fondamentale di questi microfoni, è la “ Sensibilità
“.
La sensibilità microfonica è espressa in mV/Pa (millivolt/Pascal). I valori tipici rientrano nella fascia da 2 – 100 mV/Pa. Per esempio un microfono con sensibilità 100 mV/Pa è molto sensibile, e viene utilizzato per misure di precisione. Differentemente un microfono con sensibilità di 2 mV/Pa è un microfono poco sensibile (duro), usato per rilievi in cui non è necessaria una particolare precisione.
Il microfono a noi in dotazione ha una sensibilità di 50 mV/Pa, ha quindi una discreta precisione.
I microfoni per misure fonometriche sono di due tipi:
- per misure in “ campo libero “
-
per misure in “campo
diffuso “
I microfoni per misure in campo libero hanno una risposta piana, quando investiti da un’onda piana progressiva di testa. Possono essere usati all’aperto, puntandoli verso la sorgente sonora oppure in tutti gli ambienti a patto che siano orientati verso la sorgente sonora predominante.
Usati scorrettamente, ossia ad esempio orientati con un angolo di 90° rispetto la sorgente, essi sottostimano le componenti ad alta frequenza.
Fig.5)
Esempio di microfono per misure in campo libero orientato correttamente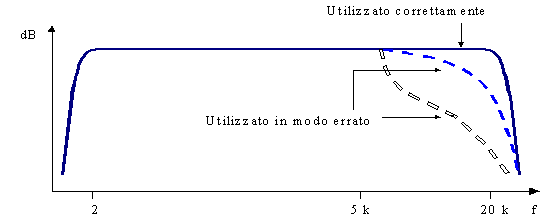 
Fig. 6) Risposta in frequenza per un microfono a campo libero
Per poter effettuare misure in ambienti con più sorgenti acustiche con presenza di rimbombi, e quindi molto ricchi di campi sonori, sono stati inventati i microfoni a campo diffuso. Usato scorrettamente, ossia orientato verso la sorgente sonora, produce una sovrastima delle alte frequenze.
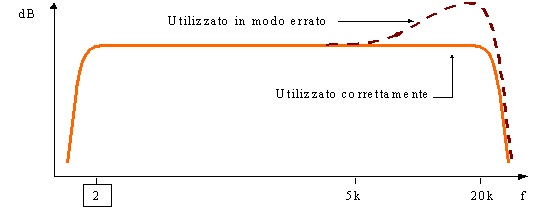
Fig. 7) Risposta in frequenza per il microfono a campo diffuso
Avendo uno dei due microfoni, è possibile usarlo per una misura in campo opposto, apportando alcune correzioni, in base all’ambiente in cui si effettua la misura.
Dovendo infatti utilizzare un microfono per campo libero in campo diffuso, si corregge la curva tramite circuiti di compensazione interni al fonometro stesso (per esempio in quello della Bruel&Kjaer).Questi circuiti correggono la curva dei livelli tramite un’operazione di filtraggio. Per il caso contrario (microfono per campo diffuso in campo libero), è sufficiente orientare lo stesso a 90° rispetto alla sorgente sonora.
E’ bene sapere che tutti questi microfoni, sono in CLASSE 1.
Questo significa che la ditta produttrice garantisce la risposta in frequenza del dispositivo entro i limiti di tolleranza indicati e previsti dalle norme.
Il microfono è costituito da due membrane: una vincolata agli estremi esposta al campo sonoro, ed una sottostante libera nella quale sono presenti delle fessure per il passaggio dell’aria. Queste membrane sono sottoposte ad una differenza di potenziale (DV), detta di polarizzazione, solitamente di 200 Volt. Le due membrane costituiscono un “ condensatore ” .
Il microfono viene di conseguenza chiamato “ microfono a condensatore “.
All’arrivo del campo sonoro, le membrane si avvicinano e si allontanano proporzionalmente alla pressione del campo, e si ha così una variazione di capacità e quindi di tensione. In serie al condensatore costituito dalle membrane se ne trova un altro, necessario per bloccare la componente continua e, permettere unicamente il passaggio della variazione di tensione.
Esistono in commercio anche microfoni autopolarizzati ,che hanno la polarizzazione internamente, ma sono meno stabili e quindi meno affidabili.
Il segnale in uscita è ora un segnale elettrico.
ADATTATORE DI IMPEDENZA
ELETTRICA (IMPEDANCE CONVERTER):
Questo dispositivo non è altro che un adattatore di impedenza che consente al sistema di funzionare.
Infatti il microfono a condensatore non funziona se chiuso su di un carico, poichè si ha l’innesco del processo di scarica del condensatore stesso (attraverso la resistenza del circuito a valle), per la quale non verrebbero rilevate le variazioni di tensione.
Chiudendo invece il circuito su di una impedenza infinita o comunque molto grande, il condensatore (microfono), non si scarica e, la variazione di tensione, viene rilevata dal circuito a valle. Questi adattatori sono comunemente costituiti da transistori unipolari (JFET – transistori ad effetto di campo) a guadagno unitario, i quali “disaccoppiano” il microfono dal resto del circuito. La caratteristica di questi dispositivi è proprio quella di riportare a monte un’impedenza elevata, e a valle una impedenza bassa sulla quale può scorrere una corrente non trascurabile.
Parecchie volte erroneamente questo stadio viene chiamato “ preamplificatore microfonico “; questo termine è improprio, perchè come già detto, il guadagno è unitario e di conseguenza non si ha amplificazione del segnale. E’ possibile inoltre porre il microfono a distanza dal fonometro tramite l’applicazione di un cavo tra l’uscita del convertitore di impedenza e lo strumento vero e proprio.
ATTENUATORE E FILTRI
DI PONDERAZIONE (AMPLIFIER
Fr WEIGHTING ATTENUATOR):
Questo dispositivo consente più operazioni:
- selezionare il fondo scala desiderato
- selezionare il tipo di ponderazione
- selezionare eventualmente l’analisi in frequenza
Selezionare il fondo scala è importante perché, un suono troppo forte, può saturare lo strumento il quale non riesce più a leggere il segnale. In questa condizione il fondo scala selezionato è troppo basso. Analogo è il discorso nel caso in cui è stato selezionato un fondo scala troppo alto per un segnale piuttosto debole, il quale non viene rilevato.
Il fondo scala va’ quindi adattato in modo che il livello sonoro, rientri nel
“ range “ di valori selezionato.
Il nostro strumento della Delta – Ohm ha un range di lavoro di 60dB per quattro fondo scala:
- 24 – 84 dB
- 44 – 104 dB per misure ambientali
- 64 – 124 dB per misure in ambienti di lavoro
- 84 – 144 dB
I più usati sono i due della fascia centrale.
Per esempio:
- il livello della voce di un professore che parla in aula con il microfono è di circa 79 – 80 dB
- il rumore di fondo causato dai soffioni di un’aula di università è di circa 49 – 50 dB
E’ possibile inoltre la scelta della ponderazione ( A,B,C,D ) oppure dell’analisi in frequenza.
Un errore in cui spesso si incorre è quello di affrontare l’analisi in frequenza del segnale già ponderato. Come visibile nello schema a blocchi, questo fonometro permette di selezionare o una o l’altra analisi del segnale, grazie ad un commutatore, che determina il collegamento del resto del sistema o con l’attenuatore, o con un sistema di filtri per l’analisi in frequenza.
INDICATORE DI
OWERFLOW e UNDERFLOW (OWERFLOW DETECTOR):
Questo stadio indica quindi quando si presentano gli stati di “ overflow “ o di “ underflow “, in modo che l’utente venga informato, e selezioni l’esatto fondo scala per poter effettuare la misura.
FILTRI
ESTERNI (EXTERNAL FILTER):
Questo insieme di filtri rende possibile l’analisi in frequenza del segnale. Negli strumenti moderni questo blocco è interno al sistema e realizzato da circuiti elettronici. I fonometri non recenti venivano collegati invece ad un dispositivo secondario, contenente appunto i filtri (a valvole) che occupavano però molto più spazio. Ecco perchè erano collegati esternamente.
RILEVATORE DI PICCO
LOGARITMICO (LOG – RMS PEAK
DETECTOR):
Passando attraverso questo stadio, il segnale precedentemente filtrato e predisposto per la ponderazione o per l’analisi in frequenza, viene innanzitutto raddrizzato (elevamento a quadrato), viene poi rilevato per farne la media efficace (RMS).
Da questo stadio viene quindi operata una conversione da logaritmico ad un valore efficace RMS.
SISTEMA DI CALCOLO
E DI INDICAZIONE (CALCULATOR
INDICATOR SYSTEM):
Il sistema di calcolo campiona il segnale con costante assegnata (FAST, SLOW, IMPULSE).
Se ad esempio, la misura viene effettuata su un intervallo di tempo di 10 minuti, ed il campionamento avviene con costante “FAST”, si ha:
10 min = 600 s
costante “Fast” = 125 ms
N = n° campioni = 600 * 8 = 4800
Come sarà specificato poi in seguito, il sistema fornisce in uscita il livello equivalente del campo.
Viene eseguita cioè dal sistema di elaborazione una media di tutti i valori campionati.
La stessa viene poi aggiornata nel tempo, ed è possibile vedere il cosiddetto “running della media”, ossia, l’andamento della media nel tempo.
DISPLAY
I vecchi strumenti erano analogici (a lancetta) e anche se non erano particolarmente precisi, fornivano un’indicazione molto intuitiva del livello di rumore misurato.
Gli strumenti moderni, con display digitale, sono sicuramente più precisi, ma anch’essi riportano al di sopra del display una “lancetta digitale” che fornisce l’indicazione analogica della stessa misura.
HOLD
(“IMPULSE” ONLY)
E’ una cella di memoria che permette di mantenere la misura eseguita fissa sul display (come un tasto pause in un registratore). Nella pratica è poco usato.
DISPOSITIVI DI USCITA DEL SEGNALE:
Il fonometro, riporta diversi tipi di prese per poter prelevare il segnale:
- presa AC pre-filter (nei fonometri recenti)
Da questa presa è possibile prelevare il segnale non ponderato, ottimo per l’analisi in frequenza.
- presa AC post-filter (nei fonometri recenti)
Da questa presa è possibile prelevare il segnale già ponderato.
- presa DC (nei fonometri non recenti)
Questa presa oggi poco usata, era dedicata a strumenti di registrazione della vecchia generazione.
- una porta seriale per la eventuale connessione ad un Pc
Le
prese AC vengono utilizzate anche per la registrazione dei campioni tramite
registratori digitali, come i DAT, schede di campionamento, Pc, ecc.
LA SCALA DEI
DECIBEL
Lo scienziato statunitense Graham Bell (1847-1922) osservò
che la sensazione sonora, alla frequenza campione di 1000 Hz, raddoppia se
l’intensità del suono che la provoca cresce di un fattore pari a circa 3.16 @ 
. Tale valore è naturalmente approssimato, in quanto la
risposta ad una variazione in pressione dipende dalle caratteristiche dell’onda
sonora, ma risulta essere abbastanza preciso. In particolare tale valore
convinse Bell ad usare una scala logaritmica per misurare la sensazione sonora:
scegliendo ad esempio una scala arbitraria alle varie pressioni si avrebbero i
seguenti risultati
|
Pressione sonora (Pa) |
Sensazione (S) |
|
0.01 |
1 |
|
0.0316 |
2 |
|
0.1 |
3 |
|
0.316 |
4 |
|
1 |
5 |
dove l’aumento di S di un’unità indica il raddoppio della sensazione.
Bell definì quindi la sensazione sonora come:
utilizzando come unità di
misura per tale grandezza il Bel [B] (dove lg indica il logaritmo in base
dieci). Si può notare come le pressioni usate non siano quelle massime
associate all’onda, ma il valor medio
efficace (RMS) mediato su un periodo, in quanto tale valore è più semplice
da calcolare. La quantità P0
è la pressione di riferimento, fissata al valore 
Pa, che corrisponde
al più basso suono udibile avente frequenza 1000 Hz. I valori ottenuti con tale
formula corrispondono bene a quelli trovati sperimentalmente, ma tale scala si
rivelò presto troppo grossolana: è per questo che ancora oggi si usano i suoi
sottomultipli, in particolare il Decibel
[dB]. Il Decibel non è una vera e propria unità di misura, ma indica il livello
della grandezza al quale è riferito:
il risultato di tale espressione è quindi il livello di pressione associato al suono.
Il Decibel viene riferito a qualsiasi grandezza di cui sia necessario avere una scala logaritmica; ad esempio le scale usate per indicare il volume di molti stereo sono espresse in decibel negativi: esse misurano il livello di attenuazione del segnale sonoro originario. Un’altra caratteristica importante del decibel risiede nella sua semplicità pratica ai fini del calcolo. Se, ad esempio, due suoni hanno una differenza nel livello della pressione pari a 6dB, attraverso semplici calcoli si può risalire alla differenza di pressione sonora che li distingue:
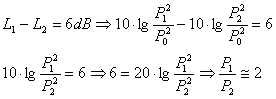
Se il segnale sonoro è trasmesso da un’onda piana
sinusoidale con velocità e pressione in fase, è utile definire un livello per
tutte le sue grandezze caratteristiche. Si definisce quindi il Livello di velocità:
che indica la velocità
dell’onda sonora rispetto alla velocità di riferimento; quest’ultimo valore si
ricava facilmente ricordando che 
:
Livello di pressione
sonora:
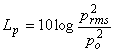
con p0 = 2 µPa
valore di riferimento.
Il Livello di intensità sonora:
dove il valore di riferimento è dato da:
Infine il Livello di densità sonora:
dove il valore di riferimento è dato da:
Utilizzando i livelli così definiti per analizzare un’onda piana sinusoidale si ottiene:
ESEMPIO : SOMMA DI
SEGNALI
Somma coerente
Dati
due segnali sonori è possibile calcolare i livelli associati nei due casi:
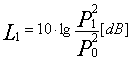
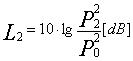
Se i due segnali sono perfettamente in fase, istante per istante le due pressioni sonore possono essere sommate per trovare un livello totale:
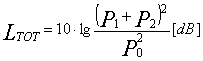
Se,
inoltre, P1=P2:
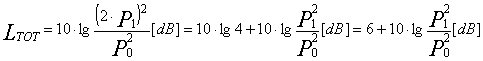
Sommando
in pressione due livelli si ottiene un incremento massimo di 6 dB.
Per cui giungiamo
all’inaspettato risultato che 
.
Somma incoerente
Nel caso in cui si abbiano a disposizione due altoparlanti che emettono lo stesso segnale, ricevere con un microfono due suoni assolutamente identici è praticamente impossibile: spesso, infatti, due segnali sono già lievemente differenti in partenza e percorrono distanze diverse prima di raggiungere il microfono. In un punto arbitrariamente lontano, quindi, a volte i segnali si sommano raddoppiando la pressione sonora, s'annullano oppure si presentano sono a fasi intermedie.
Generalmente, per somma di due livelli si
considera una somma incoerente.
Quindi, per ottenere il
livello sonoro totale si sfrutta il principio di conservazione dell'energia:
esso prevede che la densità d'energia sonora sia uguale alla somma aritmetica
delle due prese singolarmente.
Fig. 12: Somma
incoerente
Quindi, sommando le intensità dei due segnali si ottiene:
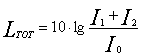
Se I1=I2 allora:
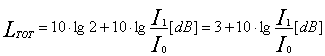
Per cui, ad esempio, 
e non 
.
Possiamo quindi affermare
che: sommando due livelli L1 ed L2, si ottiene un segnale
che è dato dal maggiore dei due incrementato al massimo di 3 dB (lo si può
notare anche dal grafico seguente).
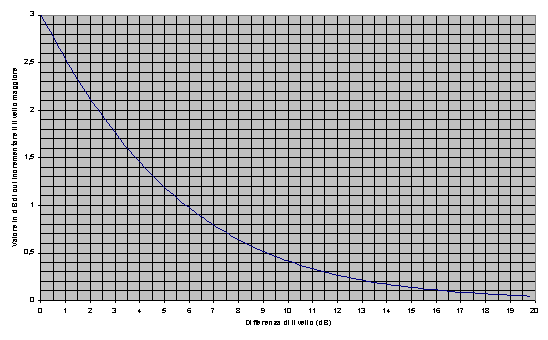
Fig. 13
Dalle proprietà del logaritmo possiamo inoltre capire che il valore da sommare al maggiore dei due suoni dipende unicamente dalla differenza di livello tra i due, non dal livello di partenza.
In fig. 13 è indicato quanto si deve sommare al livello del maggiore tra i due segnali per ottenere il livello totale.
Come si può notare, se i due livelli differiscono per più di 10 dB, l’incremento sul maggiore è sostanzialmente nullo (di soli +0,4 dB).
Ad esempio 
.
Supponiamo allora di essere in presenza di una sorgente forte e di una debole: l’orecchio umano percepisce entrambe le sorgenti, un fonometro invece soltanto la prima. Il suono è quindi trascurabile dal punto di vista del livello totale, ma è comunque udibile (sempre che non sia presente il fenomeno del mascheramento).
Interferenza
In presenza dello stesso segnale riprodotto da due altoparlanti si possono avere effetti di interferenza: vi sono, cioè, zone in cui i due segnali sono in fase (la somma avviene in pressione per un incremento massimo di 6 dB) ed altre in cui essi sono in controfase (uno ha un massimo e l’altro un minimo). In queste zone i due segnali elidono mutuamente i loro effetti. In particolare, i minimi d’intensità si trovano a distanza proporzionale a mezza lunghezza d’onda.
Gli effetti d’interferenza sono problematici quando si hanno solo due sorgenti di segnale. Con più sorgenti sarebbe praticamente impossibile trovare un punto in cui il segnale totale si annulla completamente.
L’operazione di cancellazione di un suono con un controsuono è praticamente irrealizzabile in una vasta regione: solo in condizioni geometriche molto favorevoli è ottenibile una zona di cancellazione più grande di ¼ di lunghezza d’onda. In condizioni normali, invece, le bolle silenti che si vengono a creare sono relativamente piccole (già ad una frequenza di 1000 Hz ho una lunghezza d’onda di 34 cm e quindi una bolla di raggio molto piccolo).