 :
:Onde sferiche
Si definiscono Onde sferiche quelle prodotte da una sorgente di forma sferica che immaginiamo variare il proprio volume, dilatandosi e riducendosi rispetto alla posizione di quiete, in maniera uniforme per ogni punto della superficie. Tale moto oscillatorio lungo le tre coordinate spaziali, paragonabile ad un palloncino che si gonfia e si sgonfia ciclicamente, fa sì che ciascun punto dello spazio, equidistante dalla superficie sferica in esame, venga perturbato nello stesso modo. Ciò significa medesima velocità di propagazione per l’onda generata, qualunque ne sia la direzione considerata.
La sorgente del campo sonoro è quindi una sfera in campo libero di raggio R; pulsando il suo raggio non rimane costante, ma varia in funzione del tempo t secondo la relazione R (t) = R0 + DR sin (wt), dove R0 indica il raggio della sfera a riposo.
Il campo sonoro è definito per valori di r > R.
Per avere un’idea di quanto detto si veda l’illustrazione seguente:
 :
:
Fig. 1 – sfera sorgente del campo sonoro.
Per trattare le onde sferiche è necessario ricavare l’equazione di D’Alambert in coordinate sferiche.
Per ottenere questa equazione utilizziamo un trucco affermando che il potenziale della velocità F(r, t) è funzione del tempo e della distanza dalla sfera, ma il prodotto FR rimane costante.
L’equazione da trattare risulta quindi essere la seguente:
![]() (1)
(1)
Svolgendo la derivata otteniamo:
![]() (2)
(2)
L’equazione così ottenuta è molto difficile da risolvere quindi operiamo, nella (1), la sostituzione Y = Fr ed otteniamo:
![]() (3)
(3)
La soluzione di questa equazione differenziale è data da :
![]() (4)
(4)
Il secondo termine di questa espressione rappresenta la parte di onde entranti nella sfera quindi, dato che ci occupiamo soltanto del campo sonoro all’estreno, esso non ha importanza e può essere trascurato.
Pertanto, operando la sostituzione inversa F = Y / r, otteniamo:
![]() (5)
(5)
Per far in modo che l’equazione (5) abbia significato fisico è necessario trascurare il termine immaginario dato dall’esponenziale complesso, quindi la forma definitiva del potenziale della velocità acustica è data da:
![]() (6)
(6)
Rimane ora da calcolare il valore di Y+, è necessario quindi imporre delle condizioni al contorno valide sulla pelle della sfera.
Sappiamo che:
![]() (7)
(7)
Imponiamo l’uguaglianza:
![]() (8)
(8)
Utilizzando le forme complete delle espressioni, vale a dire considerando anche la parte immaginaria, si ottiene che:
![]() (9)
(9)
Dalla (9) è immediato ricavare :
![]() (10)
(10)
Possiamo ora scrivere un’ espressione per la velocità acustica valida per un generico r > R :
![]() (11)
(11)
Calcoliamo ora l’espressione della pressione acustica e confrontiamola con quella della velocità.
Dall’espressione di F ricavata, otteniamo quella della pressione P mediante una semplice derivazione e riportiamo gli andamenti in un grafico.
![]() (12)
(12)
![]() (13)
(13)
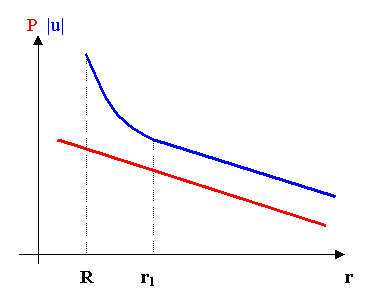
Fig. 2 – pressione e velocità sonora
Dal grafico si vede come pressione e velocità varino in fase per valori di r > rl, mentre per valori inferiori la velocità non varia più linearmente, questo è dovuto al fatto che u (r, t) dipende dal valore del prodotto kr = wr/c:
- kr < 1 : il termine che prevale nell’espressione di u è il primo (quello che si ottiene svolgendo la parentesi moltiplicando per 1) quindi ci troviamo in campo vicino alla sorgente e l’andamento non è lineare.
- kr >1 : il termine che prevale nell’espressione di u è il secondo (quello che si ottiene svolgendo la parentesi moltiplicando per jkr) quindi siamo in campo lontano dalla sorgente e l’andamento è lineare.
Per basse frequenze di pulsazione la zona in cui si estende il campo vicino è maggiore, per il fatto che k dipende da w secondo la relazione precedente, così che è necessario avere un valore di r maggiore per ottenere un prodotto kr > 1 e portarci in campo lontano, quindi per basse frequenze si ha un fenomeno d’amplificazione di queste ultime che viene detto effetto di campo vicino.
L’andamento della pressione non ha una doppia pendenza come la velocità quindi in campo vicino pressione e velocità non variano in fase, infatti, se calcoliamo l’impedenza
![]() (14)
(14)
vediamo come al variare di r varia il modulo ma anche la fase di Z, più ci avviciniamo alla sorgente, maggiormente i segnali sono sfasati.
Facciamo ora alcune considerazioni sui valori assunti dall’impedenza in due situazioni limite:
- Campo lontano:
![]() (15)
(15)
L’impedenza è la stessa che si ha per un’onda piana progressiva.
- Campo vicino:
![]() (16)
(16)
L’impedenza è puramente immaginaria, quindi pressione e velocità sono sfasate di 90° cosa che ci porterebbe ad affermare che il trasporto d’energia è nullo.
Questa situazione deriva dall’aver trascurato il termine jkr a denominatore, che in realtà non è del tutto trascurabile dato che ora ci troviamo di fronte ad un paradosso.
Fino ad ora abbiamo detto che l`impedenza e` una grandezza complessa: in quanto tale essa e` costituita da una parte reale e da una parte complessa. Osserviamo quindi graficamente l`andamento di queste due parti distinte in funzione della distanza r dal centro della sorgente sonora.
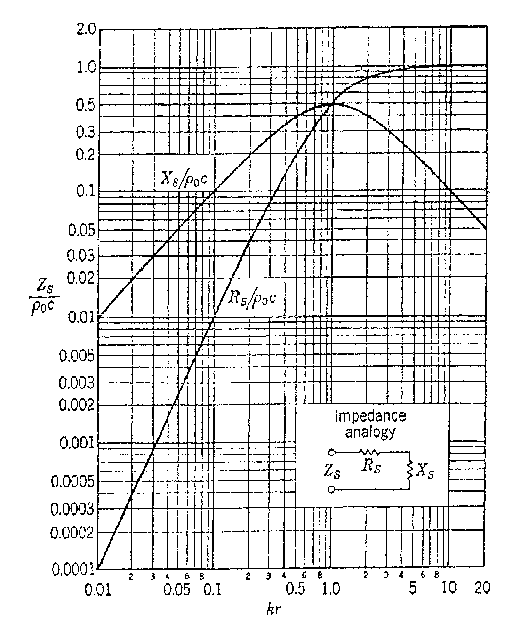
Fig. 3 – Andamento della parte reale ed immaginaria di Z(r)
![]()
E ora, dopo le considerazioni fatte, osserviamo graficamente l` andamento generale dell` Impedenza in funzione del solito raggio r. (come nel grafico precedente in ordinata e` presentata l` Impedenza Relativa, Impedenza divisa per l` Impedenza caratteristica dell`aria)
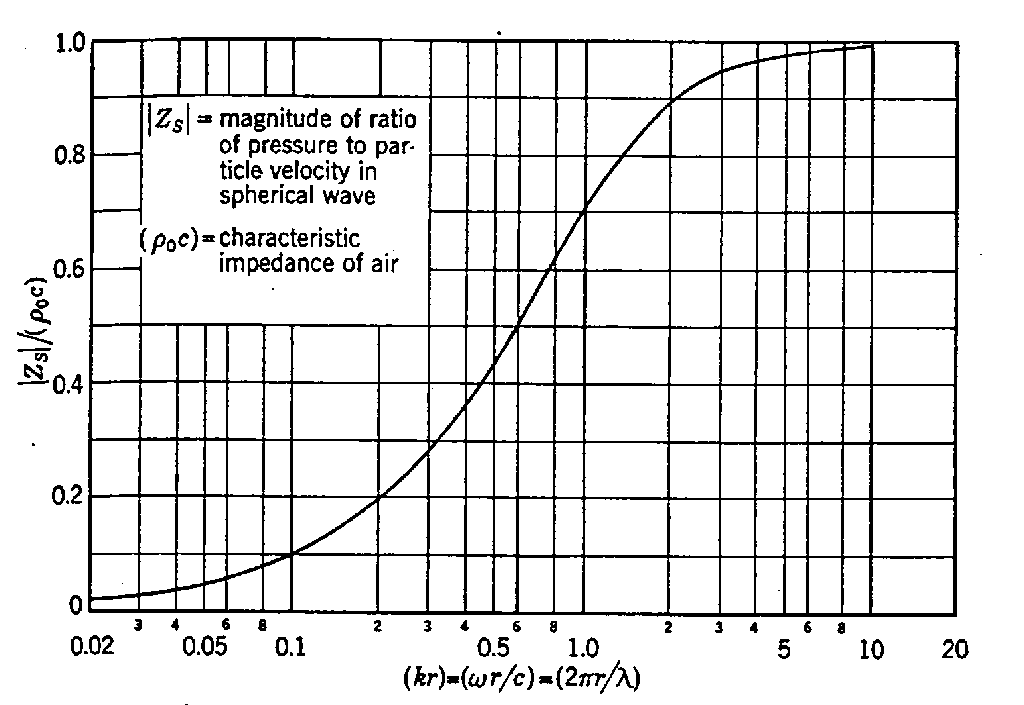
Fig. 4 – andamento del modulo di Z(r)
Si può passare,ora,all’analisi energetica delle onde sferiche fin qui illustrate.
Come è già noto l’intensità istantanea di un’onda acustica è:
![]() (16)
(16)
Mentre l’intensità media è ovviamente espressa come:
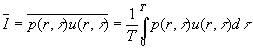 (17)
(17)
Note le espressioni di p ed u e grazie al fatto di avere già definito l’impedenza Z(r) posso semplificare l’espressione dell’intensità come segue:
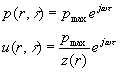 (18)
(18)
Dove ![]() è:
è:
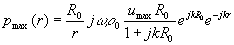 (19)
(19)
E’ utile,inoltre esprimere il valore di ![]() nel punto
nel punto ![]() :
:
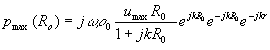 (20)
(20)
A questo punto posso effettuare l’operazione descritta in 17,la quale mi fornisce:
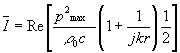 (21)
(21)
Che posso anche esprimere come:
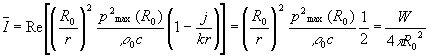 (22)
(22)
Dove W è la potenza acustica definita come l’energia sonora emessa dalla sorgente nell’unità di tempo.
I
Microfoni
Fig. 5 – esempio di microfono
Un microfono è essenzialmente un trasduttore elettroacustico in grado di tradurre le variazioni di pressioni nell’aria in oscillazioni meccaniche prima ed oscillazioni energetiche dopo.
La trasformazione da energia acustica a meccanica avviene grazie ad un organo mobile capace di entrare in vibrazione e solidale con un corpo magnetico.
Le alterazioni del campo magnetico provocate dalle oscillazioni di questo sono correlate a variazioni dell’intensità della corrente elettrica circolante nel circuito.
I microfoni possono essere suddivisi a seconda dei dispositivi di trasduzione acustica meccanica. In questo caso si dividono in:
Per quanto riguarda la trasformazione di energia da meccanica ad elettrica, i trasduttori microfonici vengono distinti in:
Inoltre esitono due principali famiglie di microfoni: dinamici e a condensatore.
Dinamico: è quel microfono equipaggiato con un trasduttore fatto con lo stesso principio fisico dell'altoparlante. Una delicata e sensibile membrana, unita ad una bobina, lavora all'interno di un magnete.Ogni spostamento della membrana dovuto alla variazione della pressione dell'aria causata dai suoni, viene tradotto in un segnale elettrico proporzionale.
Pregi: robustezza, collaudata affidabilità, buona qualità, silenziosità nel maneggio ed economia di acquisto.
Difetti: soffrono di una certa inerzia per la rilevazione di suoni molto deboli e non hanno una regolarità nella risposta in frequenza, ne consegue che i fabbricanti hanno sviluppato diversi modelli con caratteristiche specifiche per vari strumenti e voce.
Condensatore: è quel microfono equipaggiato con un trasduttore che applica il principio del condensatore. Ogni spostamento della membrana del microfono, sottile come un'ala di farfalla e placcata in oro sullo strato inferiore, fa variare la capacità di un particolare condensatore che in uscita rende segnali elettrici proporzionali al suono captato.
Pregi: straordinaria qualità di ripresa, linearità nella risposta in frequenza: è il microfono professionale per eccellenza, capace di registrare qualsiasi strumento con resa autentica e fedele. In genere ha anche la possibilità di scegliere la polarità della ripresa per mezzo di un piccolo switch posto sul corpo del microfono.
Difetti: i microfoni a condensatore veri e propri sono molto costosi e delicati, per cui se ne consiglia l'uso solo in studio. Necessitano di una alimentazione chiamata Phantom (48 volt continua), di solito equipaggiata solo in mixer di pregio. Il supporto a ragnatela per isolarlo dalle vibrazioni lascia capire che è un microfono che non può essere impugnato, che, peggio ancora, non sopporta gli urti e l'umidità delle serate nei concerti all'aperto; ragioni che lo rendono inidoneo all'utilizzo sul campo.
Polarità dei microfoni
In scena su un palco o in sala prove, tra casse spia ed amplificatori, i rientri degli altri strumenti sono sempre in agguato sul vostro microfono che, dovrebbe ignorare tutti i suoni eccettuato quello destinato al vostro strumento o voce. In realtà, al massimo si riescono ad attenuare i suoni che non sono davanti alla capsula del microfono, ed è già qualcosa; il resto è solo grande abilità dei tecnici del suono.
La qualità che determina questa capacità è la direzionalità del microfono. La direzionalità di un microfono viene espressa da alcuni aggettivi: cardioide, ipercardioide, polarità ad otto.
Cardioide (unidirezionale) significa che quel microfono ha una direzionalità a forma di cuore. Dovreste immaginare una zona grande pressappoco quanto un cuore, di fronte alla capsula del microfono; i suoni all'interno di questo spazio sono captati ottimamente, mentre al di fuori vengono notevolmente attenuati.
Ipercardioide (superdirezionale) significa che questa caratteristica polare è ancora più spinta e che la direzionalità è migliore.
Polarità ad otto (bidirezionale) significa che dinanzi al microfono esistono due aree di captazione direzionale che insieme hanno la forma di otto rovesciato. Si utilizza questa polarità ad esempio, per riprendere un duetto vocale o strumentale con un solo microfono.
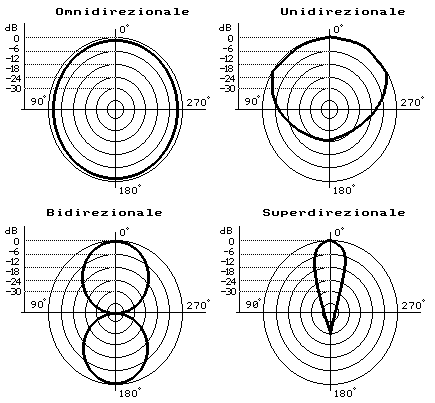
Fig. 6 – diverse polarità di microfoni
Il Fonometro

Fig.7 – esempio di fonometro
Generalità sulla fonometria
La fonometria dei suoni comprende sia i procedimenti che consentono di misurare le grandezze acustiche oggettive atte a caratterizzare il suono,quali la pressione acustica, il relativo spettro, l’andamento temporale, la potenza sonora erogata dalla sorgente, ecc.(fonometria strumentale), sia i criteri atti a fornire una valutazione degli effetti di disturbo e del rischio di danno dovuti al rumore, elaborando opportunamente i dati delle determinazioni strumentali.
I procedimenti che fanno uso di valutazioni soggettive dirette, pur costituendo ovviamente la base per l’elaborazione dei suddetti criteri, non sono di uso corrente nella fonometria tecnica, a causa della loro delicatezza e laboriosità, che li rendono applicabili soltanto da parte di operatori specializzati e ne limitano, perciò, l’impiego alle indagini di laboratorio.
Lo strumento universalmente riconosciuto per le misure fonometriche è il fonometro.
Non di rado, peraltro, le caratteristiche del suono o le esigenze del problema tecnico da risolvere rendono necessario un approfondimento dell’indagine sperimentale, onde ottenere informazioni più dettagliate e complete sulle caratteristiche del suono da valutare.
Le componenti funzionali di un fonometro possono essere rappresentate dal seguente diagramma a blocchi.
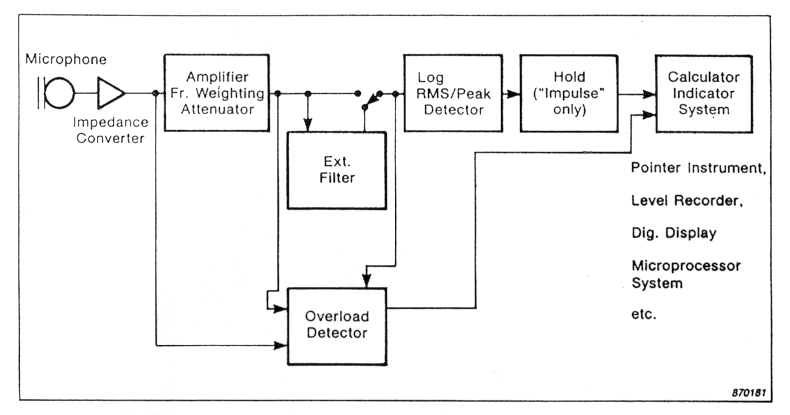
Fig. 8 – schema di funzionamento del fonometro
Microfono
Il microfono è a condensatore.
La grandezza che esprime la bontà del microfono si chiama SENSIBILITA’ e si misura in mV/Pa. In base a tale parametro si possono classificare i microfoni come:
Ad esempio un microfono con una sensibilità di 50 mV/Pa, in presenza di un livello sonoro pari a 94 dB, erogherà 50 mV, in quanto a 94 dB la pressione vale 1 Pa. Si nota che se il livello sale di 20 dB la pressione decuplica e quinidi decuplica anche il segnale in uscita, cioè a 114 dB la pressione vale 10 Pa, ed il microfono preso ad esempio erogherà 500 mV.
Attenuatore
Come si nota dalla fig. 7, l’impedance converter non viene protetto dall’overload detector, che è il blocco deputato a segnalare, tramite un’apposita spia sullo strumento, l’eventuale saturazione della circuiteria. Nonostante tale transistor goda di un notevole campo dinamico, esiste la possibilità che un rumore molto forte, quale ad esempio lo sparo di un cannone, lo faccia saturare e dia quindi luogo al fenomeno denominato clipping. Cioè quando l’impedence converter raggiunge il suo livello limite tronca in ampiezza il segnale producendo un rilievo del tutto inattendibile.
E’ importante sottolineare che tale fenomeno non viene segnalato in alcun modo dallo strumento, ma è compito di chi esegue la misura accertarsi che il livello da misurare sia compatibile con i limiti dello strumento impiegato.
Per poter misurare livelli superiori è possibile usare il cosiddetto attenuatore, che è costituito da un partitore di tensione da montare fra la capsula microfonica e l’impedence converter. L’attenuatore abbatte il segnale in ingresso di un valore costante prefissato (tipicamente 20 dB) riportandolo così nel range di funzionamento dell’impedence converter.
Amplificatore
Nei fonometri digitali di ultima generazione tale componente risulta essere superfluo, in quanto l’elettronica a valle di questo blocco è in grado di gestire segnali di pochissimi mV. Alcuni anni fa tale amplificatore era invece indispensabile, in quanto nei fonometri analogici il rumore generato dall’elettronica che li gestiva correva il rischio di sporcare il segnale.
Ponderatore in frequenza
Se inserito applica la curva di ponderazione prescelta (in genere A o C) al segnale in ingresso.
Attenuatore interno
Il fonometro ha un campo dinamico costante di circa 80 dB, ma tramite questo blocco posso attenuare il segnale in modo da avere varie scale di misura. In pratica attenuare il segnale corrisponde a regolare il fondoscala dello strumento ed una corretta regolazione consente di effettuare misure su un range ben superiore al campo dinamico del fonometro.
Ad esempio da 20 – 100 dB si può passare a 30 – 110 dB e così via. Si nota che per questo tipo di strumenti il minimo valore rilevabile è dell’ordine dei 20 dB, in quanto il rumore elettrico prodotto dal microfono vale circa 12 – 13 dB. Per misurare livelli inferiori è necessaria una strumentazione ben più raffinata che si usa solamente in laboratorio.
Filtri esterni
Sono filtri analogici d’ottava e di 1/3 d’ottava utili per fare l’analisi in frequenza. Si nota che essendo tali filtri analogici bisogna analizzare una frequenza per volta.
Convertitore rms e convertitore logaritmico
In questo blocco avviene la trasformazione del segnale da analogico a livello in dB, cioè qui avviene la conversione RMS e quella logaritmica. Per gli strumenti digitali di ultima generazione ed al top della gamma tale blocco è digitale, mentre per la maggior parte di fonometri in circolazione il convertitore è analogico.
Si nota che anche la maggior parte dei fonometri con display digitale non sono in realtà dotati di convertitore digitale.
Hold
Questo blocco era utile nei vecchi fonometri a lancetta, nei quali poteva essere molto difficile leggere il valore massimo di un evento di impulsivo. Per evitare questo fenomeno veniva applicata la costante di tempo IMPULSE che vale 35 ms se il livello sta crescendo e 1,5 s se il livello sta calando. Tramite questo accorgimento la lancetta sale molto velocemente fino al massimo, per poi calare molto lentamente dando così all’operatore la possibilità di leggere correttamente il risultato della misura.
|
NOME |
VALORE |
|
SLOW |
1 s |
|
FAST |
125 ms |
|
IMPULSE livelli crescenti |
35 ms |
|
IMPULSE livelli decrescenti |
1,5 s |
Calcolatore
Questo è un vero e proprio computer che si occupa di campionare, in genere con la costante FAST, il segnale in uscita dal convertitore e di calcolare il livello equivalente.
Si osserva che è vantaggioso usare un convertitore RMS analogico anziché digitale in quanto per campionare il segnale mi sono sufficenti 16 valori al secondo (la costante FAST vale 1/8 di secondo), mentre per campionare la forma d’onda me ne servirebbero ben 48.000 (valore standard per i registratori digitali DAT).
Ovviamente per gestire 48.000 valori al secondo anziché 16, è necessario un computer molto potente, ed è per questo motivo che solo da alcuni anni a questa parte esistono fonometri con convertitore digitale.
Memorie
MEMORIA DI DISPLAY: consente di salvare i dati visualizzati sul display a fine misura (livello minimo, livello massimo, livello equivalente…),
MEMORIA STORICA o LOG: lo strumento è in grado di archiviare in questa memoria, ad intervalli di tempo prestabiliti, i valori misurati. Si ha così la possibilità di ricostruire il profilo sonoro temporale su un lungo periodo. Più frequentemente si memorizzano i dati e più accurato sarà tale profilo, ma essendo la memoria limitata, più breve sarà il periodo di tempo analizzabile. E’ necessario dunque trovare un compromesso fra risoluzione temporale, durata della misura e memoria dello strumento,
MEMORIA STATISTICA: utile per fare l’analisi statistica.
Uscite del fonometro
SERIALE: serve a pilotare il fonometro da un computer o per scaricare i dati contenuti nella memoria log.
AC – FORMA D’ONDA: il punto nel quale viene prelevato questo segnale dipende dal particolare modello di fonometro. Tipicamente può essere fra l’attenuatore ed il ponderatore in modo da essere sensibile alle variazioni di fondoscala. Può essere collegata alla scheda audio del PC.
DC – LIVELLO: questo segnale viene prelevato subito dopo il convertitore, quindi non è il livello equivalente, ma un livello istantaneo FAST o SLOW a seconda della costante tempo utilizzata. Può essere utilizzata per pilotare una scrivente a pennino.