INDICE
Introduzione alla legge di Dalton: la teoria cinetica dei gas
Legge di Dalton
Pressione parziale e pressione totale; frazione molare e frazione ponderale
Considerazioni complessive sulla legge di Dalton
Esempi
Aria secca e vapor d’acqua
Grandezze specifiche improprie
INTRODUZIONE ALLA LEGGE DI DALTON: LA TEORIA CINETICA DEI GAS
Le proprietà elastiche dei gas e l’esistenza della pressione esercitata da un gas sulle pareti del recipiente che lo contiene avevano suggerito, fin dai tempi di Newton, che i gas fossero composti da particelle in continuo movimento. L’idea era stata sviluppata da Bernoulli intorno al 1740 e infine Joule, nel 1848, era stato in grado di arrivare ad un’espressione per la pressione di un gas contenuto in un dato volume.
Le ipotesi di partenza sono le seguenti:
Sulla base del modello cinetico si è sviluppata, nella seconda metà dell’ottocento, la teoria cinetica dei gas, che permette di arrivare a previsioni sul comportamento dei gas, verificabili sperimentalmente.
E’ inoltre importante, per proseguire il discorso, definire esplicitamente cosa si intenda per gas ideale: viene definito come gas ideale un sistema le cui coordinate termodinamiche in uno stato di equilibrio obbediscono alla seguente equazione di stato – detta appunto dei gas ideali - :
![]()
In un gas ideale, il prodotto della pressione per il volume è proporzionale al numero di moli e alla temperatura attraverso la costante universale, detta costante dei gas ideali.
LEGGE DI DALTON
Si è dunque detto di come la ipotesi fondamentali della teoria cinetica di un gas ideale suano l’assenza di iterazioni tra le molecole del gas, se non durante gli urti, e le dimensioni delle molecole trascurabili rispetto alle distanze medie tra di esse.
Se ora consideriamo una miscela di gas ideali contenuta in un volume V e alla temperatura T, le molecole di ciascun gas si comportano indipendentemente dalle molecole degli altri gas; come conseguenza si ha che la pressione esercitata dalla miscela gassosa sulle pareti del contenitore è data da:
![]() [01]
[01]
dove ![]() ,
, ![]() , …
, …
![]() rappresentano il
numero di moli di ciascun componente della miscela.
rappresentano il
numero di moli di ciascun componente della miscela.
La relazione così trovata, ricavata sperimentalmente da Dalton, è nota come legge di Dalton. Questa legge è dunque valida alle stesse condizioni alle quali è valida la legge dei gas ideali: è approssimata a pressioni moderate, ma diventa sempre più accurata quanto più si abbassa la pressione.
Pressione parziale e pressione totale; frazione molare e frazione ponderale
Definiamo pressione parziale di un dato componente i-esimo della miscela la pressione esercitata dal singolo gas come se fosse contenuto da solo nel volume V alla temperatura T. Analiticamente:
![]()
Dalla [01] si può trovare la pressione totale della miscela considerata, pari la somma delle pressioni parziali:
![]()
Graficamente si vede come la pressione totale sia somma delle pressioni parziali.
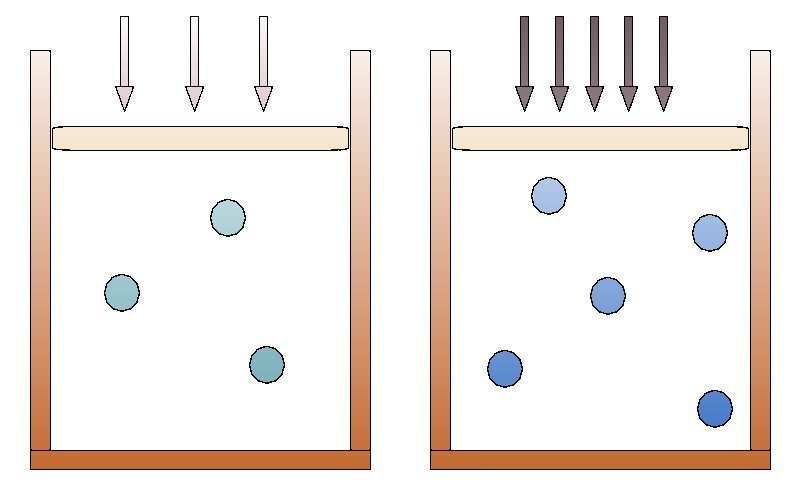
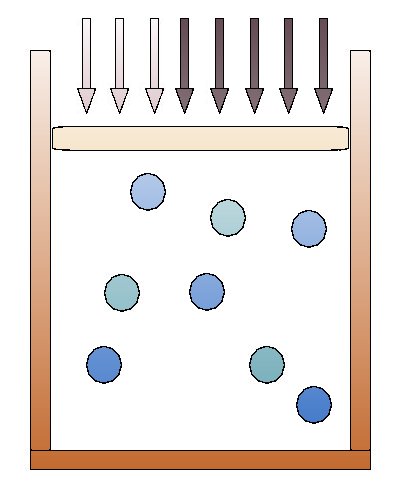
Notiamo anche che, definendo la frazione molare
![]() come rapporto
tra il numero
come rapporto
tra il numero ![]() di
moli dell’i-esimo componente ed il numero
di
moli dell’i-esimo componente ed il numero ![]() totale di moli presenti:
totale di moli presenti:
![]() [02]
[02]
si ottiene che in una miscela di gas ideali, la pressione parziale di ogni componente è data dalla pressione totale moltiplicata per la frazione molare di tale componente:
![]()
E’ utile, al fine di conoscere la composizione della miscela,
definire la frazione massica ![]() - detta anche
ponderale, essendo massa e peso in proporzionalità diretta – come
rapporto tra la massa
- detta anche
ponderale, essendo massa e peso in proporzionalità diretta – come
rapporto tra la massa ![]() dell’i-esimo componente e la massa totale del sistema
dell’i-esimo componente e la massa totale del sistema ![]() :
:
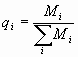 [03]
[03]
E’ evidente che sia per le frazioni molari, sia per le frazioni ponderali, valgono le seguenti relazioni:
![]()
![]()
pertanto la composizione in mole o in peso del sistema è completamente determinata quando siano assegnano un numero di frazioni molari o ponderali pari a quello dei componenti presenti meno uno.
Un’ultima relazione utile a fine pratici è quella che lega le
frazioni ponderali alle frazioni molari mediante la massa molare equivalente
![]() come:
come:
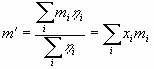
dalle relazioni [02] e [03] si trova che:
![]()
Considerazioni complessive sulla legge di Dalton
Possiamo riassumere il discorso fin qui fatto: secondo la legge di Dalton, gas ideali in un volume V alla temperatura T si comportano indipendentemente gli uni dagli altri; le pressioni dei gas perfetti sono legate tra di loro da operatori lineari, e dunque la legge di Dalton può essere vista a tutti gli effetti come un caso dell’utilizzo del principio di sovrapposizione degli effetti applicato alle pressioni dei gas ideali considerati: il gas si comporta così come se il resto del volume fosse vuoto.
Ricerca della costante relativa R per le miscele di gas ideali e altro modo di esprimere il rapporto molare
Così come fatto nel caso di un singolo, è ora possibile e
conveniente definire una costante specifica ![]() anche per le miscele di gas
ideali; per determinarne il valore, esplicito
anche per le miscele di gas
ideali; per determinarne il valore, esplicito ![]() in funzione delle masse e delle
costanti specifiche
in funzione delle masse e delle
costanti specifiche ![]() e
e ![]() di
ogni i-esimo componente.
di
ogni i-esimo componente.
Consideriamo quindi l’equazione di stato dei gas ideali:
![]()
Si può ora scrivere un sistema di N equazioni, ognuna delle quali caratterizza l’i-esimo gas presente della miscela; ovviamente vale la legge di Dalton, e dunque durante l’espansione il volume di ogni singolo aeriforme viene considerato uguale per tutti:
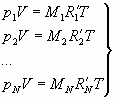 [04]
[04]
sommando membro a membro:
![]()
da cui segue che:
![]()
dove ![]() rappresenta la relazione cercata in partenza, ovvero
rappresenta la relazione cercata in partenza, ovvero ![]() è la media pesata delle
costanti
è la media pesata delle
costanti ![]() dei gas
perfetti presenti nella miscela:
dei gas
perfetti presenti nella miscela:
![]() [05]
[05]
Dal sistema [04] è inoltre possibile ricavare un’utile eguaglianza per calcolare il rapporto tra due moli i e j di due sostanze aeriformi presenti nella miscela considerata; infatti, dividendo membro a membro le due equazioni del sistema [04] relative ai gas ideali presi in esame si ottiene che:
![]() [06]
[06]
Esempio
E’ utile a questo punto considerare un esempio numerico per
quanto riguarda le considerazioni fatte; prendiamo in esame l’aria ambiente
considerata come una miscela di due gas perfetti, ossigeno (![]() ) e azoto (
) e azoto (![]() ), e calcoliamo la pressione
totale della miscela sempre grazie alla legge di Dalton:
), e calcoliamo la pressione
totale della miscela sempre grazie alla legge di Dalton:
![]()
![]()
![]()
E’ immediato, allora, calcolare il rapporto tra le due
pressioni ![]() e
e ![]() ovvero, ricordando
l’eguaglianza [06], il rapporto tra le due moli
ovvero, ricordando
l’eguaglianza [06], il rapporto tra le due moli ![]() e
e ![]() :
:
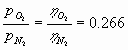
Trovato il rapporto molare tra ossigeno e azoto è immediato
ricavare anche il rapporto tra le masse di ossigeno e di azoto ![]() e
e ![]() . Intuitivamente, essendo le
molecole di ossigeno più pesanti delle molecole di azoto (peso molecolare
ossigeno
. Intuitivamente, essendo le
molecole di ossigeno più pesanti delle molecole di azoto (peso molecolare
ossigeno ![]() ; peso
molecolare azoto
; peso
molecolare azoto ![]() ), il rapporto non sarà quantitativamente lo stesso di quello trovato
precedentemente per le moli dei due gas. Il rapporto tra le due masse infatti è
dato da:
), il rapporto non sarà quantitativamente lo stesso di quello trovato
precedentemente per le moli dei due gas. Il rapporto tra le due masse infatti è
dato da:
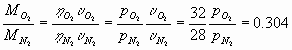
Dunque, come ci si aspettava, i due rapporti tra le masse e le moli degli aeriformi considerati sono diversi.
In ultima analisi vediamo come l’approssimazione fatta
dell’aria come una miscela di soli due gas ideali quali l’ossigeno e l’azoto è
in realtà un’ottima approssimazione per calcoli non eccessivamente accurati, o
comunque sia per calcoli ingegneristici. Con questo intento cerchiamo di
esplicitare con calcoli puramente teorici la costante specifica dell’aria ![]() : consideriamo quindi
l’aria come una miscela di gas ideali.
: consideriamo quindi
l’aria come una miscela di gas ideali.
Ricordando la relazione [05] ricavata precedentemente, si ha che:
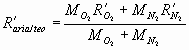
e quindi basta trovare le masse e le costante specifiche ![]() dell’ossigeno e
dell’azoto. Per quanto riguarda le masse dei due componenti, richiamando le
considerazioni fin qui fatte, facilmente si ottiene il seguente sistema
lineare:
dell’ossigeno e
dell’azoto. Per quanto riguarda le masse dei due componenti, richiamando le
considerazioni fin qui fatte, facilmente si ottiene il seguente sistema
lineare:
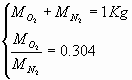
da cui si ricavano le due variabili cercate:
![]()
![]()
Anche le costanti specifiche ![]() , conoscendo i pesi molari dei
due gas
, conoscendo i pesi molari dei
due gas ![]() e
e ![]() , sono facilmente
calcolabili:
, sono facilmente
calcolabili:
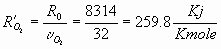
![]()
![]()
![]()
Dunque è possibile calcolare la costante specifica dell’aria
![]() :
:
![]()
Il dato sperimentale della costante specifica dell’aria ![]() è invece:
è invece:
![]()
Dunque i risultati teorici ottenuti assumendo l’aria come una miscela di gas perfetti si discostano solo leggermente dalla realtà; questo è dovuto al fatto che l’aria ambiente non è composta solo dei due gas ideali presi fin qui in esame - l’ossigeno e l’azoto -, ma anche da altri tipi di gas (come l’anidride carbonica), che non sono gas ideali a temperature e a pressione ambiente; in percentuale, la presenza di questi gas, però, è talmente bassa ( 0.97 % ) che rispetto a quella dell’ossigeno e dell’azoto ( 99.3 % ) è del tutto trascurabile per i nostri calcoli.
Di seguito viene riportata la tabella della composizione dell’aria in frazioni di volume:
|
Costituente |
Frazione in volume |
|
Azoto |
0.788110 |
|
Ossigeno |
0.20953 |
|
Argon |
0.00934 |
|
Biossido di carbonio |
0.00034 |
|
Neon |
1.82 x 10-5 |
|
Elio |
5.2 x 10-6 |
|
Metano |
1.5 x 10-6 |
|
Kripton |
1.1 x 10-6 |
|
Idrogeno |
5 x 10-7 |
|
Ossido di diazoto |
3 x 10-8 |
|
Xenon |
8.7 x 10-8 |

Esempio
Consideriamo un recipiente a pareti rigide e termicamente isolanti e diviso in due scoparti per mezzo di un divisore. All’interno dei due volumetti del contenitore ci sono distintamente due gas ideali, l’ossigeno e l’azoto.
Levando la parete divisoria si ottiene la miscelazione dei due
gas: per il primo principio della termodinamica si ha che l’energia dell’interno
sistema non cambia di valore essendo il recipiente a pareti rigide – e dunque
![]() - e termicamente
isolanti – e dunque
- e termicamente
isolanti – e dunque ![]() .
.
Essendo i gas considerati ideali, ciascuno dei due subisce un’espansione libera per raggiungere il volume totale del sistema e la corrispondente pressione parziale di miscela.
Il grafico rappresenta la situazione presa in esame con i relativi dati numerici.
|
Stato 1|2 |
|
|
Stato 3 |
Cerchiamo ora di caratterizzare lo stato della miscela.
Volume:
Troviamo inizialmente il volume del nuovo stato:
![]()
Massa:
Si possono utilizzare le equazioni di stato dei gas perfetti:
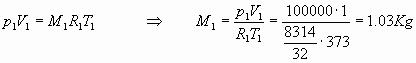
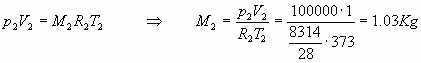
da cui, applicando la legge di Dalton, si ottiene la massa totale della miscela:
![]()
Energia:
Essendo una trasformazione adiabatica (quindi non c’è nessuno scambio di calore tra il sistema e l’esterno), anche l’energia interna del sistema si conserva:
![]()
Le uniche incognite da trovare sono ![]() e
e ![]() che si trovano facilmente dalle
equazioni di Mayer e dal rapporto g tra
che si trovano facilmente dalle
equazioni di Mayer e dal rapporto g tra ![]() , calore specifico molare a
pressione costante, e
, calore specifico molare a
pressione costante, e ![]() , calore specifico molare a volume costante.
, calore specifico molare a volume costante.
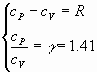
Sostituendo a ![]()
![]() e
e ![]() si ottengono i due calori
specifici :
si ottengono i due calori
specifici :
![]()
![]()
Dunque posso calcolare ![]()
![]()
Temperatura:
Conoscendo l’energia interna si può anche conoscere la
temperatura ![]() del
sistema
del
sistema
![]()
dove ![]() è la media pesata di
è la media pesata di ![]() e
e ![]() :
:
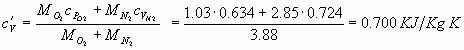
Dunque esplicitando ![]() :
:
![]()
Pressione:
Conoscendo l’equazione di stato dei gas perfetti per lo stato 3
e avendo appena ricavato la temperatura ![]() , possiamo trovare la pressione
, possiamo trovare la pressione
![]() :
:
![]()
con ![]() viene indicata la media pesata di
viene indicata la media pesata di ![]() e
e ![]() :
:
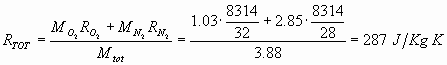
La pressione della miscela sarà dunque:
![]()
Percentuali dei due gas:
Abbiamo trovato precedentemente la messa e il volume dei due gas; possiamo adesso trovare le frazioni ponderali e molari che definiscono la miscela.
Le frazioni ponderali si trovano facilmente dai valori trovati precedentemente:
![]()
![]()
Per trovare invece le frazioni molari dobbiamo prima trovare le moli di Azoto e di Ossigeno e la mole totale della miscela:
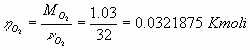
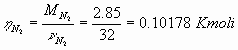
![]()
Ora possiamo trovare le frazioni molari cercate:
![]()
![]()
Entropia:
Essendo la trasformazione irreversibile, sarà naturale aspettarsi una variazione di entropia positiva, ovvero un aumento dell’entropia:
![]()
Calcoliamo ora la variazione dell’entropia ![]() facendo uso della
relazione:
facendo uso della
relazione:
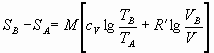
Numericamente si trova che:
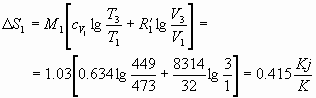
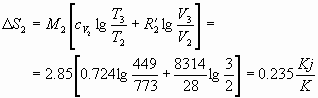
![]()
ARIA SECCA E VAPOR D’ACQUA
Un vapore, in genere, non si comporta come un gas perfetto in quanto, in condizioni normali, il volume delle sue molecole non può più essere considerato trascurabile. Tuttavia in certe condizioni anche un vapore può essere considerato così come un gas ideale: in tal caso, la miscela viene considerata una miscela di gas ideali e studiata termodinamicamente secondo quanto detto in precedenza.
Il comportamento delle miscele di soli gas differisce da quello delle miscele di gas e vapore per un fatto fondamentale: mentre nelle prime è lecita e realizzabile qualunque combinazione ponderale, nelle seconde la presenza del vapore non può mai superare un determinato valore limite, dipendente solo dalla temperatura. Conseguentemente nel primo caso si può modificare la temperatura del sistema e la composizione della miscela non cambia, mentre nel secondo caso una diminuzione di temperatura può portare a far condensare parte del vapore e quindi modificarne la composizione: se la miscela è in presenza di liquido, si ha una modifica anche per un aumento di temperatura, in quanto in tal caso vaporizza un ulteriore quantitativo di liquido.
La miscela che più comunemente si incontra nella tecnica è la miscela di aria secca e vapor d’acqua.
Definiamo aria secca la miscela composta dall’ossigeno e dall’azoto. Il vapore che forma la miscela con l’aria secca come detto può essere tratto come gas ideale, e quindi tutta la miscela viene tratta come se fosse una miscela di gas ideali.
Possiamo allora caratterizzare il vapore con l’equazione di stato dei gas ideali:
![]()
Quando veniamo vicino alle condizioni di saturazione, il vapore perde la proprietà di essere visto come un gas ideale. Spesso però si continua a studiare il sistema come se la miscela fosse ancora composta di gas ideali; questo avviene perché ho quasi sempre una percentuale di vapor d’acqua molto piccola.
Grandezze specifiche improprie
Nelle trasformazioni usuali, la massa di aria secca presente nella miscela resta costante, mentre si modifica il corrispondente quantitativo di vapor d’acqua: da ciò trae origine l’opportunità di riferire non solo la composizione in peso ma anche tutte le altre proprietà fisiche della miscela alla massa di aria secca in essa contenuta.
Titolo: Si definisce con titolo ![]() il rapporto tra la massa di
vapor d’acqua
il rapporto tra la massa di
vapor d’acqua ![]() e
la massa di aria secca
e
la massa di aria secca ![]() :
:
![]()
Inoltre dette rispettivamente ![]() e
e ![]() le pressioni parziali del vapor
d’acqua e dell’aria secca,
le pressioni parziali del vapor
d’acqua e dell’aria secca, ![]() e
e ![]() le
rispettive masse molecolari, si ha che:
le
rispettive masse molecolari, si ha che:
![]()
Grado Igrometrico:
Il grado igrometrico ![]() è definito come il rapporto tra
la massa
è definito come il rapporto tra
la massa ![]() di
vapore presente nell’unità di volume di miscela e quella
di
vapore presente nell’unità di volume di miscela e quella ![]() di vapore che potrebbe saturare
quel volume di miscela alle stesse condizioni di temperatura
di vapore che potrebbe saturare
quel volume di miscela alle stesse condizioni di temperatura ![]() :
:
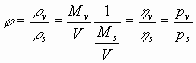
dove ![]() è la pressione di saturazione del vapor d’acqua corrispondente alla
temperatura
è la pressione di saturazione del vapor d’acqua corrispondente alla
temperatura ![]() .
.
Entalpia Specifica:
L’entalpia specifica ![]() viene definita come rapporto
tra l’entalpia totale e la massa d’aria secca presente nella miscela:
viene definita come rapporto
tra l’entalpia totale e la massa d’aria secca presente nella miscela:
![]()
dove si è utilizzata la definizione di titolo.
Arrotondando il valore del calore latente di vaporizzazione
dell’acqua, si ha che per una data miscela a temperatura ![]() e titolo
e titolo ![]() è dato da:
è dato da:
![]()