INDICE DEGLI ARGOMENTI TRATTATI
VAPORE SURRISCALDATO *
TABELLE VAPORE ACQUEO SURRISCALDATO *
CICLI TERMODINAMICI *
CICLO MACCHINA A VAPORE *
MACCHINA RANKINE *
ESERCIZI SUL CICLO RANKINE *
MACCHINA RANKINE CON SURRISCALDATORE *
La zona del vapore surriscaldato si trova nella zona più a destra del diagramma termodinamico pv sotto l’isoterma critica e a destra della curva limite superiore (vedere Fig 1). Questo vuol dire che si opera a temperatura più bassa di quella critica.
Inoltre mentre nei vapori saturi si ha coesistenza tra liquido e vapore (l’area è quella sottesa dalla campana di Andrews), in misura più o meno significativa a seconda del titolo ![]() ,nei vapori surriscaldati è presente solo il vapore in quanto il liquido è completamente evaporato, quindi si trova a temperatura più elevata di quella del liquido saturo.
,nei vapori surriscaldati è presente solo il vapore in quanto il liquido è completamente evaporato, quindi si trova a temperatura più elevata di quella del liquido saturo.
L’aggettivo "surriscaldato" non deve comunque ingannare: sebbene l’espressione sembri suscitare l’idea di "vapori caldi" cioè ad alte temperature, non sempre è così. Un esempio è l’aria, che contiene sempre una parte (anche se piccola) di vapore surriscaldato.
In realtà in quest’area ci si trova spesso a lavorare con il vapore d’acqua, poiché basta riscaldarlo un po’ per farlo passare da vapore saturo (cioè vapore in equilibrio con il liquido, in questo caso l’acqua), a vapore surriscaldato. Ci sono anche dei vantaggi pratici che invitano ad operare con il vapore surriscaldato, primo tra tutti l’incremento del rendimento di alcune macchine termiche.
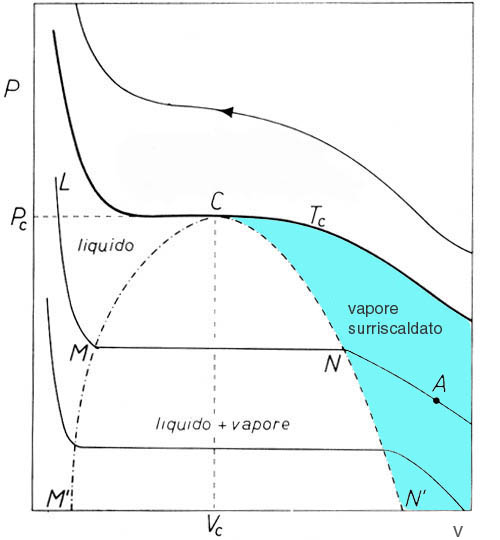
Figura 1: Diagramma pv generico: la parte evidenziata in azzurro rappresenta la zona del
vapore surriscaldato. Il simbolo Tc indica l’isoterma critica, che separa i gas dal
liquido e dal vapore. La curva CM’ è la curva limite inferiore (detta anche curva
del liquido saturo), mentre la CN’ è la curva limite superiore (o del "vapore satu-
ro"). Il percorso LMNA è un esempio di isoterma cioè una trasformazione che av-
viene a temperatura costante.
E’ importante sottolineare come in questa zona non sia disponibile un’equazione di stato (con la quale siamo abituati a lavorare) ed inoltre la pressione non dipende strettamente dalla temperatura. Questo vuol dire che possiamo avere infinite coppie pT, relazionate secondo una tabella a doppia entrata come quella sottostante, che rappresenta alcuni parametri termodinamici fondamentali del vapore d’acqua.
|
p (bar) |
p1 |
pn |
|||||||
|
t(°C) |
T(K) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Tabella 1
: Esempio struttura di tabella a doppia entrata pT, per un numero indefinito di pressioni(p1…..pn) e di temperature. Ad ogni coppia pT viene associato un volume specifico,
un’energia interna specifica, un’entalpia specifica e un’entropia specifica.
Le tabelle che seguono riportano le proprietà termodinamiche (v,u,h,s) del vapore acqueo surriscaldato a diverse pressioni e temperature. Per comodità di lettura viene elencato un tabulato per una determinata pressione a cui corrispondono le sopra indicate grandezze specifiche esaminate a varie temperature (fino a 1000°C).
TABELLE VAPORE ACQUEO SURRISCALDATO
|
p (bar) |
0.1 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
0 (tsat) |
14.7 |
2437.91 |
2584.64 |
8.1502 |
|
50 |
14.9 |
2443.88 |
2592.58 |
8.1749 |
|
100 |
17.2 |
2515.51 |
2687.47 |
8.4479 |
|
150 |
19.5 |
2587.88 |
2783.00 |
8.6882 |
|
200 |
21.8 |
2661.28 |
2879.54 |
8.9038 |
|
250 |
24.1 |
2735.97 |
2977.32 |
9.1002 |
|
300 |
26.5 |
2812.07 |
3076.52 |
9.2813 |
|
350 |
28.8 |
2889.70 |
3177.24 |
9.4497 |
|
400 |
31.1 |
2968.90 |
3279.53 |
9.6076 |
|
450 |
33.4 |
3049.75 |
3383.46 |
9.7565 |
|
500 |
35.7 |
3132.27 |
3489.06 |
9.8977 |
|
550 |
38.0 |
3216.50 |
3596.37 |
10.0322 |
|
600 |
40.3 |
3302.46 |
3705.41 |
10.1608 |
|
650 |
42.6 |
3390.17 |
3816.20 |
10.2842 |
|
700 |
44.9 |
3479.64 |
3928.75 |
10.4029 |
|
750 |
47.2 |
3570.87 |
4043.05 |
10.5174 |
|
800 |
49.5 |
3663.85 |
4159.11 |
10.6282 |
|
850 |
51.8 |
3758.58 |
4276.92 |
10.7355 |
|
900 |
54.1 |
3855.04 |
4396.46 |
10.8396 |
|
950 |
56.5 |
3953.20 |
4517.69 |
10.9408 |
|
1000 |
58.8 |
4053.03 |
4640.60 |
11.0393 |
|
p (bar) |
0.5 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
81.33 (tsat) |
3.24 |
2483.86 |
2645.88 |
7.5939 |
|
100 |
3.42 |
2511.62 |
2682.54 |
7.6947 |
|
150 |
3.89 |
2585.62 |
2780.09 |
7.9401 |
|
200 |
4.36 |
2659.86 |
2877.66 |
8.1580 |
|
250 |
4.82 |
2734.98 |
2976.01 |
8.3556 |
|
300 |
5.28 |
2811.34 |
3075.54 |
8.5372 |
|
350 |
5.75 |
2889.12 |
3176.46 |
8.7060 |
|
400 |
6.21 |
2968.44 |
3278.91 |
8.8642 |
|
450 |
6.67 |
3049.37 |
3382.95 |
9.0132 |
|
500 |
7.13 |
3131.96 |
3488.64 |
9.1546 |
|
550 |
7.60 |
3216.24 |
3596.02 |
9.2891 |
|
600 |
8.06 |
3302.24 |
3705.11 |
9.4178 |
|
650 |
8.52 |
3389.98 |
3815.94 |
9.5412 |
|
700 |
8.98 |
3479.47 |
3928.52 |
9.6600 |
|
750 |
9.44 |
3570.72 |
4042.85 |
9.7745 |
|
800 |
9.90 |
3663.72 |
4158.94 |
9.8853 |
|
850 |
10.4 |
3758.46 |
4276.77 |
9.9926 |
|
900 |
10.8 |
3854.93 |
4396.32 |
10.0967 |
|
950 |
11.3 |
3953.10 |
4517.56 |
10.1979 |
|
1000 |
11.8 |
4052.93 |
4640.47 |
10.2964 |
|
p (bar) |
1 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
99.63 (tsat) |
1.69 |
2506.07 |
2675.47 |
7.3594 |
|
100 |
1.70 |
2506.65 |
2676.23 |
7.3614 |
|
150 |
1.94 |
2582.76 |
2776.40 |
7.6134 |
|
200 |
2.17 |
2658.06 |
2875.29 |
7.8343 |
|
250 |
2.41 |
2733.74 |
2974.35 |
8.0333 |
|
300 |
2.64 |
2810.42 |
3074.30 |
8.2157 |
|
350 |
2.87 |
2888.40 |
3175.49 |
8.3850 |
|
400 |
3.10 |
2967.86 |
3278.13 |
8.5434 |
|
450 |
3.33 |
3048.89 |
3382.31 |
8.6927 |
|
500 |
3.57 |
3131.56 |
3488.11 |
8.8341 |
|
550 |
3.80 |
3215.90 |
3595.57 |
8.9688 |
|
600 |
4.03 |
3301.95 |
3704.73 |
9.0976 |
|
650 |
4.26 |
3389.73 |
3815.62 |
9.2210 |
|
700 |
4.49 |
3479.25 |
3928.24 |
9.3398 |
|
750 |
4.72 |
3570.53 |
4042.61 |
9.4544 |
|
800 |
4.95 |
3663.55 |
4158.72 |
9.5652 |
|
850 |
5.18 |
3758.31 |
4276.57 |
9.6726 |
|
900 |
5.41 |
3854.79 |
4396.14 |
9.7767 |
|
950 |
5.64 |
3952.96 |
4517.40 |
9.8779 |
|
1000 |
5.88 |
4052.80 |
4640.32 |
9.9764 |
|
p (bar) |
2.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
120.23 (tsat) |
0.886 |
2529.50 |
2706.65 |
7.1271 |
|
150 |
0.960 |
2576.41 |
2768.82 |
7.2795 |
|
200 |
1.08 |
2654.41 |
2870.47 |
7.5066 |
|
250 |
1.20 |
2731.24 |
2971.00 |
7.7086 |
|
300 |
1.32 |
2808.57 |
3071.80 |
7.8926 |
|
350 |
1.43 |
2886.96 |
3173.55 |
8.0628 |
|
400 |
1.55 |
2966.70 |
3276.56 |
8.2218 |
|
450 |
1.67 |
3047.94 |
3381.03 |
8.3715 |
|
500 |
1.78 |
3130.76 |
3487.04 |
8.5132 |
|
550 |
1.90 |
3215.23 |
3594.67 |
8.6481 |
|
600 |
2.01 |
3301.38 |
3703.97 |
8.7770 |
|
650 |
2.13 |
3389.24 |
3814.97 |
8.9006 |
|
700 |
2.24 |
3478.82 |
3927.68 |
9.0195 |
|
750 |
2.36 |
3570.15 |
4042.12 |
9.1342 |
|
800 |
2.48 |
3663.21 |
4158.29 |
9.2450 |
|
850 |
2.59 |
3758.00 |
4276.18 |
9.3524 |
|
900 |
2.71 |
3854.50 |
4395.79 |
9.4566 |
|
950 |
2.82 |
3952.69 |
4517.08 |
9.5578 |
|
1000 |
2.94 |
4052.54 |
4640.02 |
9.6563 |
|
p (bar) |
3.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
133.55 (tsat) |
0.606 |
2543.57 |
2725.32 |
6.9919 |
|
150 |
0.634 |
2570.80 |
2760.97 |
7.0778 |
|
200 |
0.716 |
2650.67 |
2865.55 |
7.3115 |
|
250 |
0.796 |
2728.70 |
2967.61 |
7.5166 |
|
300 |
0.875 |
2806.70 |
3069.29 |
7.7022 |
|
350 |
0.954 |
2885.52 |
3171.59 |
7.8733 |
|
400 |
1.03 |
2965.54 |
3275.00 |
8.0329 |
|
450 |
1.11 |
3046.99 |
3379.74 |
8.1830 |
|
500 |
1.19 |
3129.97 |
3485.97 |
8.3251 |
|
550 |
1.26 |
3214.56 |
3593.78 |
8.4602 |
|
600 |
1.34 |
3300.81 |
3703.21 |
8.5892 |
|
650 |
1.42 |
3388.74 |
3814.31 |
8.7129 |
|
700 |
1.50 |
3478.39 |
3927.11 |
8.8319 |
|
750 |
1.57 |
3569.77 |
4041.62 |
8.9467 |
|
800 |
1.65 |
3662.87 |
4157.85 |
9.0576 |
|
850 |
1.73 |
3757.69 |
4275.79 |
9.1650 |
|
900 |
1.80 |
3854.21 |
4395.43 |
9.2692 |
|
950 |
1.88 |
3952.42 |
4516.75 |
9.3705 |
|
1000 |
1.96 |
4052.29 |
4639.72 |
9.4690 |
|
p (bar) |
4.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
143.63 (tsat) |
0.463 |
2553.57 |
2738.55 |
6.8959 |
|
150 |
0.471 |
2564.50 |
2752.83 |
6.9299 |
|
200 |
0.534 |
2646.84 |
2860.53 |
7.1706 |
|
250 |
0.595 |
2726.13 |
2964.17 |
7.3789 |
|
300 |
0.655 |
2804.82 |
3066.76 |
7.5662 |
|
350 |
0.714 |
2884.06 |
3169.63 |
7.7382 |
|
400 |
0.773 |
2964.38 |
3273.42 |
7.8984 |
|
450 |
0.831 |
3046.03 |
3378.46 |
8.0489 |
|
500 |
0.889 |
3129.17 |
3484.91 |
8.1913 |
|
550 |
0.948 |
3213.88 |
3592.88 |
8.3266 |
|
600 |
1.01 |
3300.23 |
3702.45 |
8.4558 |
|
650 |
1.06 |
3388.25 |
3813.66 |
8.5796 |
|
700 |
1.12 |
3477.96 |
3926.55 |
8.6987 |
|
750 |
1.18 |
3569.39 |
4041.13 |
8.8135 |
|
800 |
1.24 |
3662.52 |
4157.41 |
8.9245 |
|
850 |
1.30 |
3757.38 |
4275.40 |
9.0319 |
|
900 |
1.35 |
3853.93 |
4395.08 |
9.1362 |
|
950 |
1.41 |
3952.16 |
4516.43 |
9.2375 |
|
1000 |
1.47 |
4052.03 |
4639.42 |
9.3360 |
|
p (bar) |
5.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
151.86 (tsat) |
0.375 |
2561.24 |
2748.69 |
6.8213 |
|
200 |
0.425 |
2642.93 |
2855.39 |
7.0592 |
|
250 |
0.474 |
2723.52 |
2960.70 |
7.2709 |
|
300 |
0.523 |
2802.93 |
3064.21 |
7.4599 |
|
350 |
0.570 |
2882.60 |
3167.66 |
7.6329 |
|
400 |
0.617 |
2963.21 |
3271.85 |
7.7937 |
|
450 |
0.664 |
3045.07 |
3377.17 |
7.9446 |
|
500 |
0.711 |
3128.37 |
3483.84 |
8.0872 |
|
550 |
0.758 |
3213.21 |
3591.98 |
8.2228 |
|
600 |
0.804 |
3299.66 |
3701.69 |
8.3522 |
|
650 |
0.851 |
3387.75 |
3813.01 |
8.4761 |
|
700 |
0.897 |
3477.53 |
3925.98 |
8.5953 |
|
750 |
0.943 |
3569.00 |
4040.64 |
8.7102 |
|
800 |
0.990 |
3662.18 |
4156.98 |
8.8212 |
|
850 |
1.04 |
3757.07 |
4275.01 |
8.9287 |
|
900 |
1.08 |
3853.64 |
4394.72 |
9.0330 |
|
950 |
1.13 |
3951.89 |
4516.10 |
9.1343 |
|
1000 |
1.18 |
4051.78 |
4639.12 |
9.2328 |
|
p (bar) |
10.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
179.91 (tsat) |
0.194 |
2583.65 |
2778.10 |
6.5865 |
|
200 |
0.206 |
2621.91 |
2827.87 |
6.6940 |
|
250 |
0.233 |
2709.92 |
2942.61 |
6.9247 |
|
300 |
0.258 |
2793.22 |
3051.17 |
7.1229 |
|
350 |
0.283 |
2875.19 |
3157.67 |
7.3011 |
|
400 |
0.307 |
2957.30 |
3263.89 |
7.4650 |
|
450 |
0.330 |
3040.24 |
3370.68 |
7.6180 |
|
500 |
0.354 |
3124.35 |
3478.46 |
7.7621 |
|
550 |
0.378 |
3209.83 |
3587.47 |
7.8988 |
|
600 |
0.401 |
3296.77 |
3697.87 |
8.0290 |
|
650 |
0.425 |
3385.27 |
3809.74 |
8.1535 |
|
700 |
0.448 |
3475.37 |
3923.16 |
8.2732 |
|
750 |
0.471 |
3567.09 |
4038.16 |
8.3884 |
|
800 |
0.494 |
3660.47 |
4154.79 |
8.4997 |
|
850 |
0.518 |
3755.51 |
4273.05 |
8.6074 |
|
900 |
0.541 |
3852.21 |
4392.95 |
8.7118 |
|
950 |
0.564 |
3950.55 |
4514.48 |
8.8133 |
|
1000 |
0.587 |
4050.50 |
4637.62 |
8.9119 |
|
p (bar) |
25.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
223.99 (tsat) |
0.0800 |
2603.15 |
2803.09 |
6.2574 |
|
250 |
0.0870 |
2662.56 |
2880.07 |
6.4085 |
|
300 |
0.0989 |
2761.57 |
3008.82 |
6.6438 |
|
350 |
0.110 |
2851.86 |
3126.25 |
6.8403 |
|
400 |
0.120 |
2939.04 |
3239.29 |
7.0148 |
|
450 |
0.130 |
3025.44 |
3350.79 |
7.1746 |
|
500 |
0.140 |
3112.09 |
3462.05 |
7.3233 |
|
550 |
0.150 |
3199.52 |
3573.75 |
7.4633 |
|
600 |
0.159 |
3288.01 |
3686.26 |
7.5960 |
|
650 |
0.169 |
3377.73 |
3799.83 |
7.7225 |
|
700 |
0.178 |
3468.81 |
3914.60 |
7.8436 |
|
750 |
0.188 |
3561.32 |
4030.71 |
7.9599 |
|
800 |
0.197 |
3655.32 |
4148.21 |
8.0720 |
|
850 |
0.207 |
3750.84 |
4267.18 |
8.1804 |
|
900 |
0.216 |
3847.91 |
4387.65 |
8.2853 |
|
950 |
0.225 |
3946.53 |
4509.63 |
8.3871 |
|
1000 |
0.235 |
4046.69 |
4633.13 |
8.4861 |
|
p (bar) |
50.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
263.99 (tsat) |
0.0394 |
2597.14 |
2794.35 |
5.9734 |
|
300 |
0.0453 |
2697.96 |
2924.54 |
6.2083 |
|
350 |
0.0519 |
2808.68 |
3068.40 |
6.4493 |
|
400 |
0.0578 |
2906.59 |
3195.66 |
6.6458 |
|
450 |
0.0633 |
2999.65 |
3316.16 |
6.8185 |
|
500 |
0.0686 |
3090.94 |
3433.78 |
6.9758 |
|
550 |
0.0737 |
3181.83 |
3550.25 |
7.1218 |
|
600 |
0.0787 |
3273.02 |
3666.48 |
7.2589 |
|
650 |
0.0836 |
3364.89 |
3783.00 |
7.3886 |
|
700 |
0.0885 |
3457.68 |
3900.14 |
7.5122 |
|
750 |
0.0933 |
3551.56 |
4018.15 |
7.6305 |
|
800 |
0.0981 |
3646.64 |
4137.19 |
7.7441 |
|
850 |
0.103 |
3743.01 |
4257.38 |
7.8535 |
|
900 |
0.108 |
3840.73 |
4378.83 |
7.9593 |
|
950 |
0.112 |
3939.84 |
4501.59 |
8.0618 |
|
1000 |
0.117 |
4040.36 |
4625.71 |
8.1612 |
|
p (bar) |
100.0 bar |
|||
|
t(°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
311.06 (tsat) |
0.0180 |
2544.43 |
2724.69 |
5.6140 |
|
350 |
0.0224 |
2699.17 |
2923.40 |
5.9443 |
|
400 |
0.0264 |
2832.39 |
3096.47 |
6.2119 |
|
450 |
0.0298 |
2943.33 |
3240.85 |
6.4189 |
|
500 |
0.0328 |
3045.78 |
3373.65 |
6.5966 |
|
550 |
0.0356 |
3144.55 |
3500.93 |
6.7561 |
|
600 |
0.0384 |
3241.70 |
3625.36 |
6.9029 |
|
650 |
0.0410 |
3338.23 |
3748.29 |
7.0398 |
|
700 |
0.0436 |
3434.73 |
3870.53 |
7.1687 |
|
750 |
0.0461 |
3531.56 |
3992.62 |
7.2911 |
|
800 |
0.0486 |
3628.99 |
4114.92 |
7.4078 |
|
850 |
0.0511 |
3727.19 |
4237.73 |
7.5196 |
|
900 |
0.0535 |
3826.34 |
4361.25 |
7.6272 |
|
950 |
0.0559 |
3926.52 |
4485.65 |
7.7311 |
|
1000 |
0.0583 |
4027.82 |
4611.05 |
7.8316 |
|
p (bar) |
200.0 bar |
|||
|
t (°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
365.81 (tsat) |
0.0594 |
2293.12 |
2409.81 |
4.9270 |
|
400 |
0.00994 |
2619.24 |
2818.08 |
5.5540 |
|
450 |
0.0127 |
2806.17 |
3060.07 |
5.9017 |
|
500 |
0.0148 |
2942.83 |
3238.20 |
6.1401 |
|
550 |
0.0166 |
3062.36 |
3393.46 |
6.3348 |
|
600 |
0.0182 |
3174.02 |
3537.58 |
6.5048 |
|
650 |
0.0197 |
3281.47 |
3675.33 |
6.6582 |
|
700 |
0.0211 |
3386.48 |
3809.10 |
6.7994 |
|
750 |
0.0225 |
3490.02 |
3940.29 |
6.9308 |
|
800 |
0.0239 |
3592.75 |
4069.81 |
7.0544 |
|
850 |
0.0252 |
3695.11 |
4198.34 |
7.1715 |
|
900 |
0.0265 |
3797.46 |
4326.38 |
7.2831 |
|
950 |
0.0277 |
3900.06 |
4454.32 |
7.3898 |
|
1000 |
0.0290 |
4003.13 |
4582.47 |
7.4925 |
|
p (bar) |
300.0 bar |
|||
|
t (°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
375 |
0.00179 |
1737.77 |
1791.44 |
3.9304 |
|
400 |
0.00279 |
2067.36 |
2151.05 |
4.4728 |
|
500 |
0.00868 |
2820.69 |
3081.05 |
5.7904 |
|
600 |
0.0115 |
3100.55 |
3443.92 |
6.2331 |
|
700 |
0.0137 |
3335.85 |
3745.69 |
6.5606 |
|
800 |
0.0156 |
3555.62 |
4024.32 |
6.8333 |
|
900 |
0.0175 |
3768.49 |
4291.94 |
7.0718 |
|
1000 |
0.0192 |
3978.80 |
4554.69 |
7.2867 |
|
p (bar) |
500.0 bar |
|||
|
t (°C) |
v (m³/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg) |
|
375 |
0.00156 |
1638.56 |
1716.53 |
3.7639 |
|
400 |
0.00173 |
1788.05 |
1874.60 |
4.0031 |
|
500 |
0.00389 |
2525.46 |
2720.08 |
5.1725 |
|
600 |
0.00611 |
2941.99 |
3247.61 |
5.8178 |
|
700 |
0.00773 |
3230.55 |
3616.92 |
6.2190 |
|
800 |
0.00908 |
3479.83 |
3933.64 |
6.5290 |
|
900 |
0.0103 |
3710.27 |
4224.43 |
6.7882 |
|
1000 |
0.0114 |
3930.54 |
4501.10 |
7.0146 |
Lo svantaggio della situazione è evidente: nel caso del vapore saturo ci si poteva spostare lungo la tabella di riga in riga mentre ora occorre analizzare sia ogni riga che ogni colonna per trovare i valori richiesti di entapia specifica h, volume specifico v, entropia specifica s ed energia interna u.
E’ quindi molto più difficile affrontare un problema termodinamico che riguardi vapori surriscaldati dal punto di vista tabellare. Ci sono tuttavia molti altri diagrammi che possono aiutare notevolmente l’analisi del problema in esame, visualizzando i parametri termodinamici da diversi punti di vista. Ricordiamo che utilizzando la superficie (p,v,T) e il diagramma (p,v) che se ne ricava, è possibile determinare il valore delle coordinate termodinamiche T,u,h,s in funzione della pressione p e del volume specifico v. Questo vuol dire che è possibile traslare qualsiasi curva che venga tracciata sul diagramma (p,v) su un altro diagramma che riporti altre coordinate.
Un esempio è il diagramma temparatura-entropia (T,s) (s = entropia specifica) riportato sotto, molto utile per studiare i vapori surriscaldati:
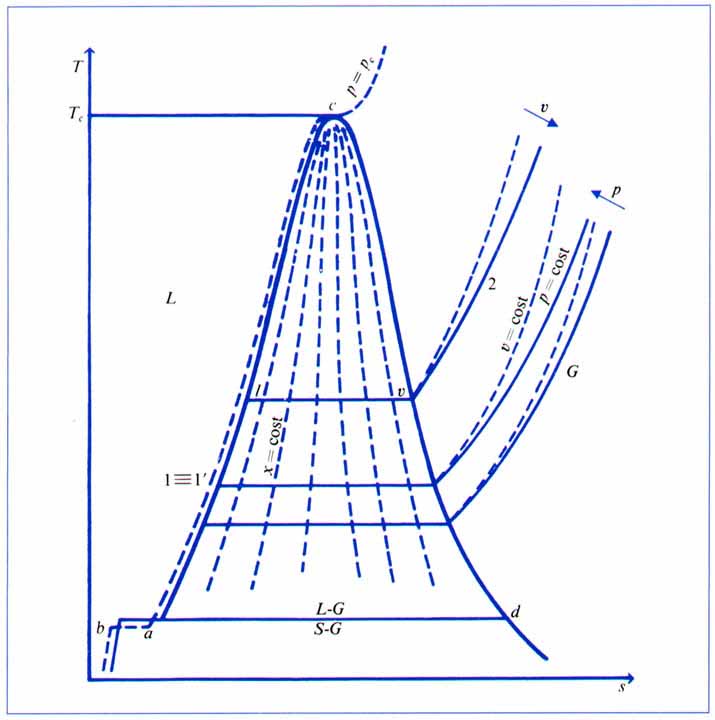
Figura 2
: Diagramma termodinamico T,s. Le curve tratteggiate sotto la campana di Andrewsrappresentano le curve isotitolo.
Si può vedere come sia più semplice analizzare gli stati termodinamici in questa ottica: inoltre, la comodità di avere l’entropia specifica s in ascissa è di notevole importanza se il problema da risolvere riguarda l’immissione di vapore surriscaldato in una turbina. Tale trasformazione infatti è isoentropica (cioè l’entropia della sostanza rimane costante) e quindi identificabile semplicemente con una retta verticale.
Naturalmente è possibile lavorare anche con il solito grafico (p,v), ma l’analisi ne uscirà più complicata.
Un ulteriore vantaggio che deriva dall’utilizzo di questo diagramma è l’immediatezza con la quale è possibile la risoluzione di calcoli tecnici, in quanto esso permette la lettura diretta della quantità di calore scambiato lungo una trasformazione e quindi anche la determinazione di ![]() .
.
Infatti, lungo una qualsiasi trasformazione (almento internamente invertibile e quindi tracciabile su un diagramma termodinamico), vale la relazione:
![]() (1)
(1)
Ricavando ora il calore q tramite integrazione, otteniamo:
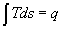 (2)
(2)
La conclusione è che, mentre nel diagramma pv, l’area sottesa dalla curva di trasformazione indicava il lavoro L (eseguito dal sistema, quindi positivo), adesso l’area sottesa indica il calore scambiato. Ciò si intuisce chiaramente dalla definizione stessa di entropia s.
Il grafico sottostante mette in luce queste considerazioni:
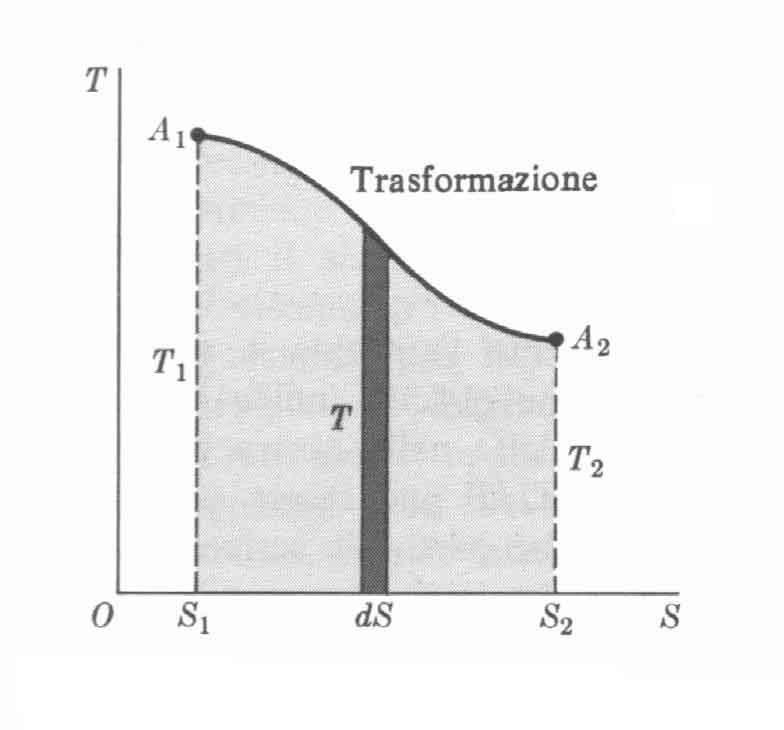
NOTA: il calore assorbito durante il processo è dato dall’area ombreggiata. (T1 è la temperatura nello stato A1, mentre T2 quella dello stato A2).
E’ importante anche il senso di percorrenza della curva sul diagramma, da cui è possibile risalire al segno della quantità di calore scambiata: se ad esempio un sistema riceve calore isotermicamente (quindi a temperatura costante), tale processo sarà rappresentato da una linea retta orizzontale corrispondente a un dato valore di temperatura. In questo caso, il verso di percorrenza sarà da sinistra a destra poiché vi è stato un aumento di entropia s.
Nel caso di una trasformazione ciclica, l’area racchiusa dalla relativa curva nel diagramma T,s, se percorsa in senso orario, è proporzionale alla quantità ![]() , mentre l’area di curva da sinistra a destra è altresì proporzionale a
, mentre l’area di curva da sinistra a destra è altresì proporzionale a ![]() .
.
E’ quindi possibile in questo caso valutare direttamente il valore del coefficiente economico:
![]() (3)
(3)
In particolare, nel caso di un ciclo di Carnot, calcolare ![]() è molto semplice dato che le trasformazioni isoterme sono tratti paralleli all’asse delle ascisse mentre quelle adiabatiche reversibili sono segmenti paralleli all’asse delle ordinate (isoentropiche). In pratica, il ciclo di Carnot risulta espresso da un rettangolo.
è molto semplice dato che le trasformazioni isoterme sono tratti paralleli all’asse delle ascisse mentre quelle adiabatiche reversibili sono segmenti paralleli all’asse delle ordinate (isoentropiche). In pratica, il ciclo di Carnot risulta espresso da un rettangolo.
Assumendo che la quantità di calore fornita al sistema sia pari a ![]() e che quella totale, scambiata durante il ciclo, valga
e che quella totale, scambiata durante il ciclo, valga ![]() , si può ricavare subito il coefficiente economico di Carnot:
, si può ricavare subito il coefficiente economico di Carnot:
![]() (4)
(4)
(dove ![]() >
>![]() ).
).
Non c’è solo il diagramma T,s che può illustrare da altri punti di vista una trasformazione termodinamica. In particolare va preso in considerazione anche il diagramma h,s (entalpia, entropia), rappresentato nella figura sottostante:
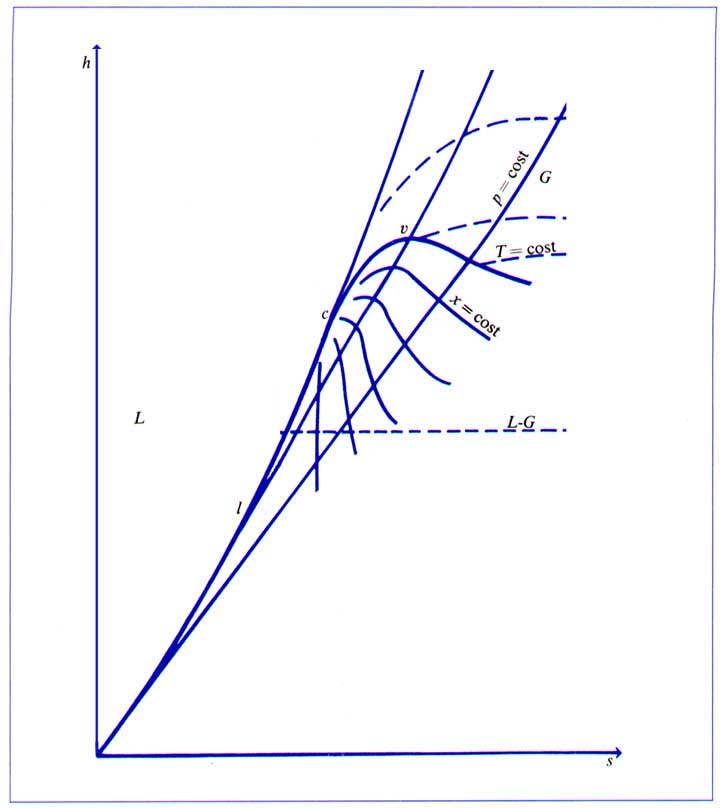
Figura 3
: Diagramma (h,s) per un sistema monocomponente (detto anche di Mollier), limitato atemperature superiori a quelle del punto triplo.
C’è una significativa analogia tra questo diagramma e quello T,s di prima. Infatti, preso il ![]() dell’acqua (pari a 4187 J/(kg K)) e poste per convenzione h=s=0 al punto triplo, si può notare che il valore dell’entalpia coincide praticamente con quello della temperatura per cui nella regione del liquido entrambi i diagrammi sono uguali.
dell’acqua (pari a 4187 J/(kg K)) e poste per convenzione h=s=0 al punto triplo, si può notare che il valore dell’entalpia coincide praticamente con quello della temperatura per cui nella regione del liquido entrambi i diagrammi sono uguali.
In realtà è spesso utile per operare su vapori surriscaldati fare un ingrandimento della zona superiore del diagramma (un esempio è riportato nella figura successiva) in modo da poter discriminare con buona precisione anche le curve a pressione costante.
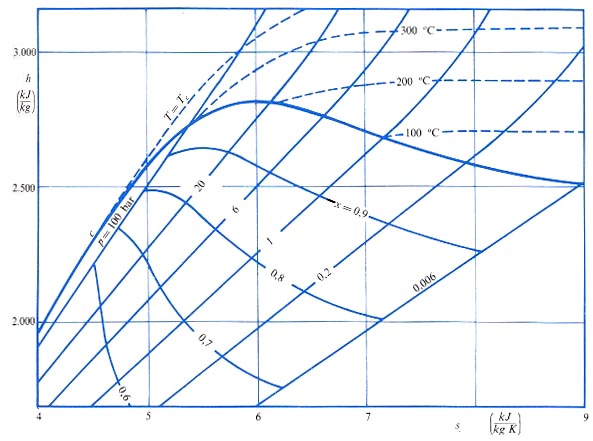
Figura 4: Zoom del diagramma di Mollier (h,s) per il vapore d’acqua surriscaldato a diverse temperature. Sull’asse delle ascisse l’entropia specifica viene indicata in kJ/(Kg K), così come l’entalpia specifica in quello delle ordinate.
E’ facile anche in questo grafico ricavare le coordinate termodinamiche (non l’energia interna specifica u); un altro vantaggio è dato dalla presenza delle curve isotitolo che consentono di studiare anche i vapori saturi (in cui è presente parte di vapore e parte di liquido).
Proprio per questo e per la capacità di visualizzare a colpo d’occhio la quantità di lavoro o di calore scambiato tra sistema e ambiente esterno, trova applicazioni nello studio dei sistemi aperti.
Il diagramma di Mollier non si pone come alternativa stretta alle tabelle riguardanti i vapori saturi e surriscaldati: infatti può essere un valido strumento di analisi per via grafica nei problemi in cui esso può essere utilizzato con sufficiente approssimazione.
Per situazioni più professionali, oltre a dotarsi di tabelle esaustive e complete, occorrerebbe possedere un diagramma di Mollier (o una parte di esso a seconda dei problemi in esame) di notevoli dimensioni.
Una delle applicazioni più importanti della termodinamica, in ambito ingegneristico, consiste nello studio e nella realizzazione di sistemi complessi che siano in grado di convertire in modo continuo (anche se non completamente), calore in lavoro.
Si tratta evidentemente di macchine "cicliche" nelle quali, diagrammando i vari processi di trasformazione e ricavando l’area contenuta all’interno del ciclo, otteniamo il lavoro L risultato del processo ciclico stesso.
Possiamo infatti affermare che sia nel diagramma pv che in quello T,s le aree racchiuse da un qualsiasi ciclo rappresentino il lavoro ottenuto dal ciclo (osservare le due figure sottostanti).
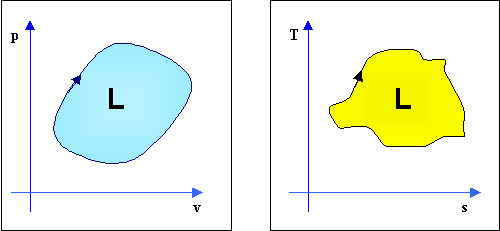
Figure 5-6: Ciclo termodinamico in un diagramma pv e Ts: nel primo ciclo il lavoro è dato
dall’area azzurra mentre nel secondo da quella gialla.
In realtà questa considerazione può sembrare in contrasto con quanto illustrato nel paragrafo precedente sui diagrammi termodinamici, in particolare con le proprietà del grafico T,s: tuttavia basta pensare alla modalità di funzionamento di una macchina termica semplice:
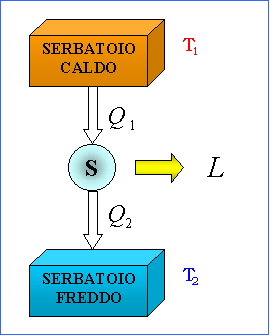
Figura 7
: Schema di lavoro di una macchina termica semplice DIRETTA.
dove ![]() . In sintesi il sistema (l’oggetto al centro) assorbe una quantità di calore
. In sintesi il sistema (l’oggetto al centro) assorbe una quantità di calore ![]() dal serbatoio di calore 1 (caldo) posto a temperatura
dal serbatoio di calore 1 (caldo) posto a temperatura ![]() e poi ne cede una quantità
e poi ne cede una quantità ![]() al serbatoio freddo a temperatura
al serbatoio freddo a temperatura ![]() . Al termine verrà prodotto dal sistema un lavoro
. Al termine verrà prodotto dal sistema un lavoro ![]() sull’esterno.
sull’esterno.
Adottiamo questo principio al caso di una trasformazione ciclica in un diagramma T,s.
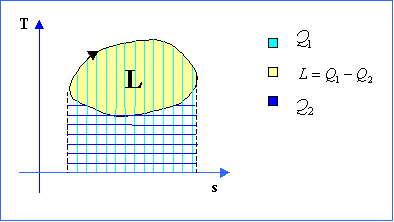
Figura 8
: Il lavoro di una macchina diretta in un ciclo nel diagramma Ts.
Quindi tanto maggiore è l’area del ciclo, tanto maggiore sarà il lavoro effettuato dalla macchina.
Consideriamo il diagramma pv sottostante:
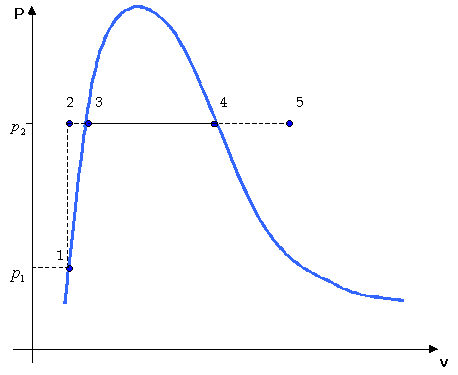
Figura 9
: Esempio di un ciclo macchina a vapore (non richiuso).Si parte dallo stato 1 in cui la pressione è bassa (ad esempio 1 bar). Supponiamo che la sostanza in esame sia acqua liquida e che a tale pressione occupi un volume determinato. Introduciamo quindi l’acqua in una pompa che sia in grado di aumentarne la pressione (trasformazione 1à 2) mantenendo inalterato il suo volume. Ciò è rappresentato nel diagramma pv con una retta verticale.
Il fluido viene introdotto in una caldaia nella quale viene riscaldato, vaporizzato e surriscaldato (processi 2à 3, 3à 4 e 4à 5).
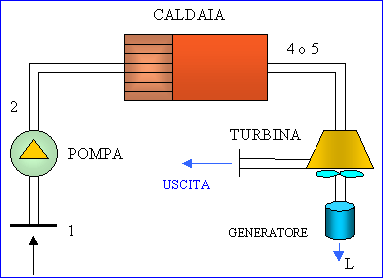
Figura 10
: Esempio di ciclo Macchina a Vapore in cui vengono indicate numericamente le variefasi del processo e le apparecchiature utilizzate durante la trasformazione.
Solitamente la turbina generica viene sostituita da un modello analogo dotato però di doppia palettatura; il moto del rotore del generatore è provocato dall’afflusso di vapore (che può essere surriscaldato) dalla caldaia, con velocità molto elevate.
Sostanzialmente la turbina ha lo scopo di "prendere" energia dal vapore in uscita dalla caldaia e di trasferirla al generatore elettrico, in rotazione con velocità angolare ![]() . Tale velocità è imposta dalla frequenza di rete fissata a 50Hz.
. Tale velocità è imposta dalla frequenza di rete fissata a 50Hz.
Possiamo individuare sul diagramma pv una fase 5à
6 in cui il vapore ha ceduto la sua energia all’albero rotante e si ha una diminuzione di pressione dal valore ![]() al valore di partenza
al valore di partenza ![]() .
.
Questa trasformazione è un’isoentropica (adiabatica reversibile) rappresentabile con una curva decrescente fino ad intersecare la curva limite (Figura 11).
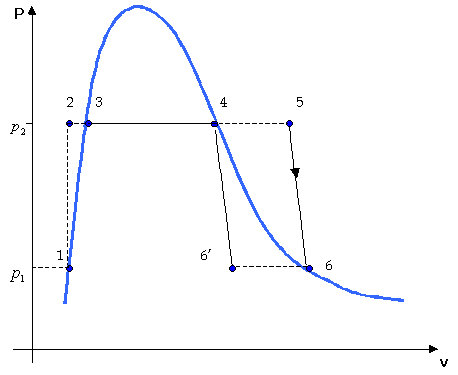
Figura 11
: Variante del ciclo precedente con surriscaldamento e cessione di E, per cui si ritorna al valore di pressione iniziale ![]() .
.
Nei casi più generali in cui il processo della macchina si conclude alla fase 4, tale curva si troverà sotto quella limite (vedere 4à 6’).
Il vapore può viaggiare a velocità elevatissime, per cui non in tutte le situazioni il liquido si forma immediatamente, anche se le condizioni termodinamiche sono opportune. L’elemento che è maggiormente sollecitato durante il processo è indubbiamente la turbina, non solo a causa degli "urti" violenti che subisce da parte del vapore a forte velocità; infatti tale apparato può essere danneggiato seriamente (e a volte anche irrimediabilmente), se assieme al vapore sono presenti delle goccioline d’acqua. Quest’ultime infatti provocano notevoli sforzi meccanici che a lungo andare possono degradare le palette.
Bisogna considerare che una goccia d’acqua possiede una quantità di moto circa 1000 volte maggiore di quella posseduta dal vapore acqueo e quindi le conseguenze da urto sono notevoli.
Per scongiurare questi pericoli si ricorre molto spesso a sensori di controllo che, all’insorgere di qualche anomalia, interrompono in via precauzionale la turbina onde evitare danni più seri. In alcune centrali elettriche più datate invece i problemi legati al malfunzionamento delle apparecchiature è più frequente, a volte anche a causa della scarsa manutenzione applicata alle stesse.
Il rischio è evidente: se la centrale è costretta per qualche motivo ad interrompere il servizio ciò si ripercuote negativamente sulla zona circostante, in quanto viene interrotta la fornitura di energia elettrica con conseguenze prevedibili.
Nel procedimento sopra descritto, viene definita "fase di espansione di turbina" quella in cui dal generatore elettrico è possibile produrre lavoro meccanico L. Al termine del ciclo il vapore può essere scaricato nell’ambiente, ma si andrebbe incontro ad uno "spreco" di acqua che può sempre tornare utile.
Un esempio di questa situazione sono le locomotive a vapore che infatti dovevano essere regolarmente approvvigionate di materiale combustibile per la produzione di vapore, con molti svantaggi sia dal punto di vista energetico che dal punto di vista pratico.
Un modo per riutilizzare quel vapore sarebbe quello di fornire calore a temperature più basse, riducendo così gli sprechi: applicazioni di questo principio si possono trovare nella fornitura di acqua calda per usi domestici o in luoghi pubblici. E’ presente comunque un contesto di mercato in cui inserire l’acqua calda.
D’altra parte, in alcune città italiane (Brescia in testa a tutte) la distribuzione dell’acqua calda avviene già da tempo per via centralizzata (ne fa uso circa il 95% dei cittadini). Tecnicamente questa soluzione si definisce "teleriscaldamento".
Invece di avere caldaie in ogni abitazione (o condominio), la produzione complessiva di acqua calda viene delegata ad un piccolo numero di centrali che sfruttano appunto questo tipo di macchina termica.
Il vantaggio è evidente: oltre al risparmio nell’acquisto e nel mantenimento di una caldaia, vi è la possibilità di ottenere di acqua calda corrente: l’altra faccia della medaglia è la maggiorazione di prezzo che viene applicata sulle tariffe di quanti sfruttino questo servizio (comunque riservato ad una popolazione ristretta alle vicinanze delle centrali).
Per chi si trova più lontano dalle "zone di prima fascia" (dove un eventuale allacciamento al servizio sarebbe sconveniente), le centrali termo-elettriche provvedono a fornire corrente elettrica, che può essere utilizzata per pilotare opportune "pompe di calore".
Il fatto di avere un’unica (o in numero ridotto) centrale di produzione consente di minimizzare gli sprechi (come sopra descritto) e nello stesso tempo migliorare la qualità degli impianti termici (queste centrali sono tenute sempre sotto controllo da parte sia del personale addetto alla manutenzione, sia da strumenti elettronici sofisticati).
Altro vantaggio non indifferente è quello di limitare l’emissione di agenti inquinanti nell’ambiente, adottando "filtri" appositi nei condotti di uscita. Questo aspetto è molto importante per soddisfare le normative che regolano questi processi.
Tuttavia, la tecnica del teleriscaldamento è applicabile con successo quasi esclusivamente ad aree ridotte, per lo più comunali a causa degli inevitabili problemi logistici (e burocratici) che ne comporterebbe l’adozione su scala nazionale.
Abbiamo detto che la sostanza sulla quale si basa il ciclo della macchina a vapore è l’acqua. Ad ogni modo, non si tratta di "acqua" qualsiasi, ma opportunamente depurata, filtrata, demineralizzata e a PH controllato.
L’impiego di liquido diverso da questo provocherebbe danni alla turbina. E’ ovvio che possedere acqua a un tale livello di purezza richiede molti soldi, ed è per questo che si cerca di riutilizzarla (il più possibile), chiudendo il ciclo. Il verso di percorrenza è ORARIO (assunto come positivo) e se viene prodotto lavoro L vuol dire che si è generata E meccanica da E termica.
Sappiamo che per realizzare un ciclo termodinamico che produca la massima quantità di lavoro a parità di calore entrante, l’ideale sarebbe avere a disposizione una macchina di Carnot. D’altra parte però, la macchina di Carnot è ideale e quindi irrealizzabile nel caso pratico. Inoltre essa opera su un ciclo reversibile.
Tuttavia è possibile ottenere buoni risultati adottando la macchina Rankine, di cui la figura sottostante rappresenta gli elementi più significativi.
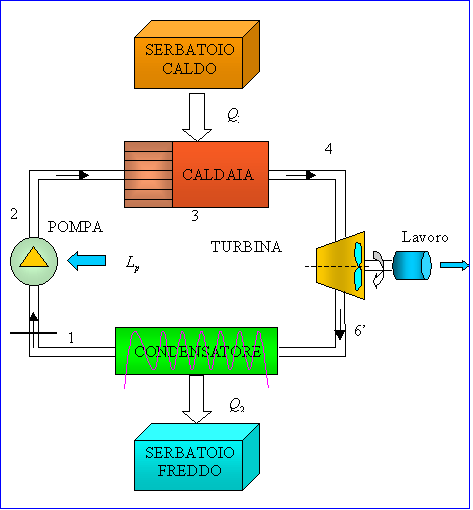
Figura 12: Elementi fondamentali del ciclo di una macchina di Rankine.
La macchina nel complesso è un sistema chiuso, ma è scomponibile in 4 sotto sistemi che invece sono tutti aperti (elencati qui sotto):
PRINCIPIO DI FUNZIONAMENTO
1à
2: l’acqua nella fase liquida subisce una trasformazione isoentropica da parte della pompa, che è un sistema aperto che non scambia calore. Viene quindi indicato con il simbolo ![]() il lavoro necessario a "portare l’acqua alla caldaia".
il lavoro necessario a "portare l’acqua alla caldaia".
2à 3 , 3à 4 , (4à 5): l’acqua arriva alla caldaia dove viene per prima cosa riscaldata fino alla temperatura di vaporizzazione e poi vaporizzata mantenendo costante la temperatura fino a farla diventare "vapore saturo secco" (con titolo uguale a 1).
5à 6: Questo vapore saturo secco passa attraverso la turbina (che non scambia calore), e si espande ad entropia costante compiendo lavoro (siamo sotto la curva limite superiore).
6à 1: il vapore saturo a bassa pressione viene portato completamente nella fase liquida, a pressione e temperatura costanti, tramite una "serpentina" posta all’interno del condensatore nella quale scorre acqua fredda e quindi viene ceduto del calore al serbatoio freddo (osservare il diagramma generale della pagina precedente).
Analiticamente:
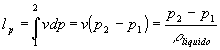 (9)
(9)(10)
Per focalizzare concretamente queste analisi, osserviamo i corrispondenti grafici. La figura 15 mostra (colorato di verde) il lavoro totale del ciclo Rankine sotto forma di area del ciclo. Infatti ricordiamo che nel diagramma pv l’area di un ciclo rappresenta il lavoro prodotto dal ciclo stesso. La figura 16 invece mostra, nel diagramma Ts, il calore di combustione ![]() (Area1+Area2) e quello di condensatore
(Area1+Area2) e quello di condensatore ![]() (area sottesa dal tratto 6’à
1 di ritorno).
(area sottesa dal tratto 6’à
1 di ritorno).
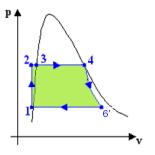
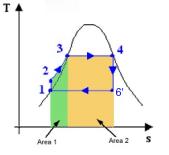
Figure 13-14
: Lavoro complessivo prodotto dal ciclo Rankine e calori in gioco.Di seguito si riportano alcuni esercizi sul ciclo Rankine.
Lo scopo di questi esercizi è quello di studiare la macchina dal punto di vista termodinamico e di calcolare il coefficiente economico ![]() .
.
La macchina è quindi senza surriscaldamento. Riportiamo i dati indicati nelle unità di misura del sistema internazionale:
![]() e
e ![]()
![]() e
e ![]()
e osserviamo il ciclo nel diagramma Ts.
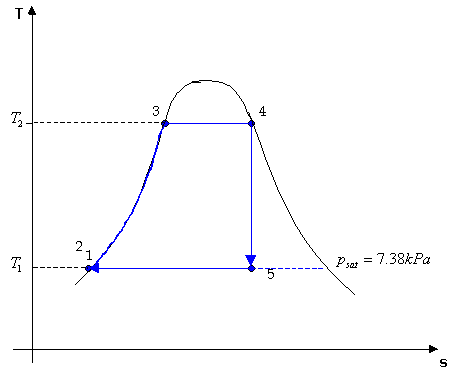
Figura 15:
Diagramma Ts del ciclo di Rankine in esame.Sappiamo che il coefficiente economico ![]() ; è quindi possibile risolvere l’esercizio calcolando i salti di entalpia.
; è quindi possibile risolvere l’esercizio calcolando i salti di entalpia.
Si può quindi riscrivere: ![]() ; occorre adesso valutare l’entalpia di questi 4 punti.
; occorre adesso valutare l’entalpia di questi 4 punti.
Calcoliamo il salto ![]() ,
,
che rappresenta il lavoro della pompa sul sistema.
Procedendo, si ha che:
![]()
Mancano però i dati (entalpia e titolo) corrispondenti al punto 5. Ricavo quindi il valore dell’entalpia in 4:
![]() ,
,
dove ![]() è l’entalpia specifica del liquido nel punto 1 ed è un valore tabellato, pari a 167.5 kJ/kg. Per calcolare
è l’entalpia specifica del liquido nel punto 1 ed è un valore tabellato, pari a 167.5 kJ/kg. Per calcolare ![]() possiamo sfruttare la formula nota:
possiamo sfruttare la formula nota:
![]()
Il titolo ![]() non lo conosciamo ma sappiamo invece
non lo conosciamo ma sappiamo invece ![]() che è uguale ad 1 (dato implicito del problema). Sapendo inoltre che nel diagramma T,s la trasformazione 4à
5 è una retta verticale, abbiamo che :
che è uguale ad 1 (dato implicito del problema). Sapendo inoltre che nel diagramma T,s la trasformazione 4à
5 è una retta verticale, abbiamo che :
![]() , dove
, dove
![]()
Dall’uguaglianza sopra, è ovvio concludere che:
![]() , da cui
, da cui ![]()
Riusciamo allora a calcolare ![]() , che rappresenta il lavoro di turbina. Sostituendo i risultati trovati possiamo infine determinare il coefficiente economico:
, che rappresenta il lavoro di turbina. Sostituendo i risultati trovati possiamo infine determinare il coefficiente economico:
![]()
Tale valore può sembrare a prima vista un po’ poco, ma in realtà è buono. Infatti, proviamo a confrontarlo con il coefficiente economico della macchina di Carnot ![]() , operante tra quelle temperature:
, operante tra quelle temperature:
Otteniamo: ![]() ;
;
Quindi, il rapporto: ![]() , che è molto buono.
, che è molto buono.
In realtà il confronto tra i coefficienti economici è mal posto perché abbiamo sprecato del lavoro, se per esempio pensiamo alla temperatura di combustione adiabatica (1500÷1800°C). Noi infatti lavoriamo a "soli" 250°C.
Uno spreco minore si ha negli impianti turbogas che operano con vapori a 1500°C.
Si può migliorare il ciclo di Rankine, in modo da porre fine al problema delle goccioline d’acqua che urtano violentemente le palette della turbina (nello stato 5 dell’es. precedente il titolo era 0.714<1, quindi una parte di liquido esiste). Il meccanismo è quello di introdurre un serpentino riscaldatore, come mostrato nella figura successiva:
MACCHINA RANKINE CON SURRISCALDATORE
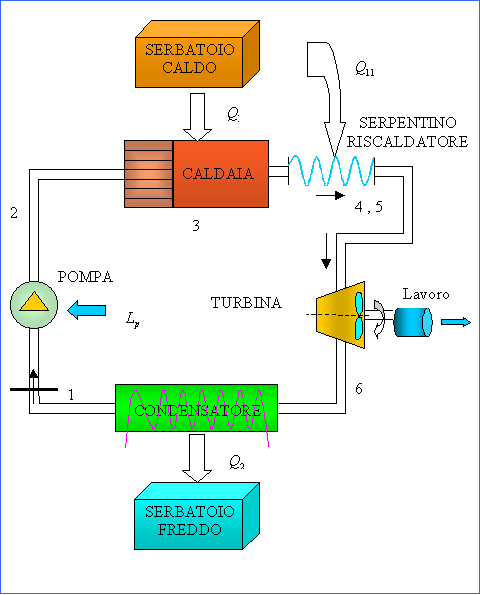
Figura 16: Esempio di ciclo Rankine con surriscaldatore.
Proviamo ora a rifare l’esercizio di prima introducendo un nuovo stato (6) in quanto nella trasformazione 4à 5 il vapore è stato surriscaldato (tramite il serpentino riscaldatore) a 500°C. Gli altri dati del problema sono uguali.
Possiamo vedere come varia il ciclo in questo caso:
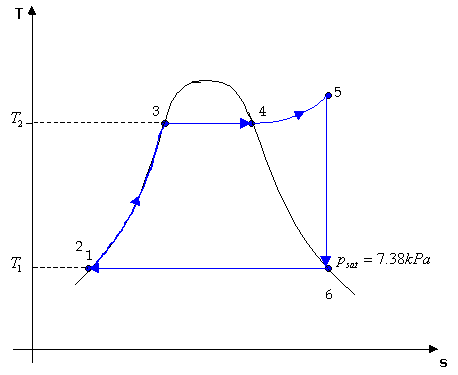
Figura 17
: Diagramma Ts del ciclo di Rankine con surriscaldatore
Il "nuovo" coefficiente economico è dato da:
![]() ; il lavoro di pompa rimane uguale:
; il lavoro di pompa rimane uguale: ![]() .
.
Quindi calcoliamo il salto di entalpia:
![]()
e sostituendo i valori numerici, si ottiene:
![]()
Si nota subito che il calore scambiato in caldaia ha ora un termine in più.
Analogamente, non conoscendo ![]() , procediamo all’uguaglianza delle entropie
, procediamo all’uguaglianza delle entropie
![]()
Si ha che:
![]()
Ma allora da: ![]() si ricava:
si ricava: ![]()
Questo vuol dire che adesso ci siamo spostati molto più a destra rispetto a prima, dove ![]() .
.
E’ possibile trovare le entalpie:
![]()
e ![]()
A questo punto il coefficiente economico:
![]() (meglio di prima)
(meglio di prima)
Confrontandolo con il coefficiente di Carnot tra queste temperature di esercizio:
![]() e dunque
e dunque ![]()
In verità potremmo non essere soddisfatti di questa modifica in quanto rispetto al coefficiente di Carnot abbiamo perso terreno, ma al solito il confronto è mal posto.
Stiamo infatti trascurando il 2°principio della termodinamica, poiché analizzando la quantità di exergia, il ciclo Rankine è notevolmente migliore della macchina di Carnot. Infatti il ciclo Rankine non lavora con serbatoi a temperatura costante e quindi si riescono a seguire le cadute di temperatura.
C’è allora una grande resa exergetica.
Per sfruttare un altro po’ di calore in più si potrebbe preriscaldare il combustibile tramite lamiere calde, tramite un recuperatore dei fumi in uscita a 70°C.
Si cerca quindi di espellere i fumi alla più alta temperatura possibile.
In conclusione si può dire che con infiniti cicli di Carnot si potrebbe estrarre tutto il calore dai fumi (procedimento ideale e irrealizzabile praticamente).
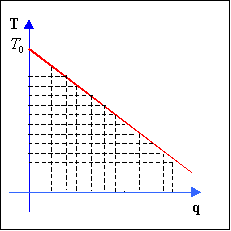
Figura 18
: Estrazione del calore tramite infiniti cicli di Carnot