TRASMISSIONE DEL CALORE PER IRRAGGIAMENTO

Scambio termico per irraggiamento

Con scambio termico per irraggiamento si intende il trasporto di energia sotto forma di calore tramite onde elettromagnetiche.

Perché avvenga la trasmissione del calore tra due corpi non è necessaria la presenza di un mezzo trasmissivo interposto, come avveniva per la conduzione o la convezione, ma la si può ottenere anche attraverso il vuoto.

Onde elettromagnetiche

Nelle onde elettromagnetiche si ha un trasporto di energia dovuto all’oscillazione del campo elettrico e del campo magnetico .

La propagazione dell’onda è rettilinea ed avviene lungo l’asse x, come mostrato in figura 1; l’oscillazione del vettore avviene in modo ortogonale alla direzione dell’onda, ed il vettore di induzione magnetica è a sua volta ortogonale al vettore campo elettrico, cioè i due campi si collocano su piani ortogonali.

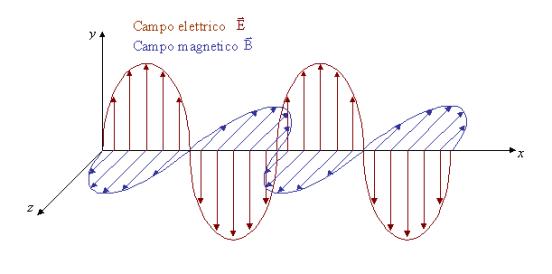
Figura 1; Rappresentazione vettoriale dell'onda elettromagnetica lungo l'asse x.

Il paragone con le onde acustiche è molto semplice, in particolare in acustica il campo è rappresentato vettori di intensità e pressione, in analogia con quello elettromagnetico. La differenza è che per le prime è necessario un mezzo per la propagazione, per esempio l’aria o un solido, perché il trasporto di energia acustica è legata all’oscillazione delle molecole.

Se l’oscillazione del campo magnetico e di quello elettrico sono in fase ( come mostrato nella figura precedente ), si ha il massimo trasporto di energia. Per tale motivo anche tramite onde elettromagnetiche si può sviluppare il fenomeno di onde stazionarie, cioè è possibile avere un campo di valore elevato che non trasporta energia.

Si supponga di avere per esempio un’antenna che irradia onde radio all’interno di un ambiente riverberante, come mostrato in figura 2; si verrà a creare un campo elettromagnetico riverberante, poiché le onde non possono uscire dall’ambiente, ed il trasporto di energia sarà nullo, pur avendo all’interno valori di campo elettrico e magnetico molto elevati.

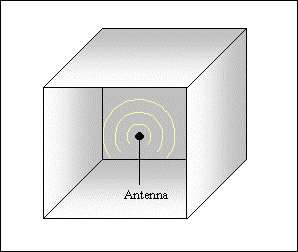
Figura 2; Camera riverberante con all'interno un'antenna.

Inizialmente si pensava che il trasporto di onde elettomagnetiche avvenisse solo nel vuoto e non nella materia. In seguito alla teoria della realtività di Einstain si è scoperto il legame tra massa ed energia, tramite la legge E=mc² . Tale teoria fu poi dimostrata una volta scoperto il fotone, particella dotata di una massa molto piccola e che compone la luce, che è la forma più comune di onda elettromagnetica. Quest’ultima consente il trasporto di energia ma necessita di una piccola quantità di materia ( i fotoni appunto ) perché ciò avvenga. Il fotone ha una caratteristica corpuscolare, per cui risulta essere quantizzato.

Per tale motivo il trasporto di energia nelle onde elettromagnetiche è quantizzato; però, se ci si riferisce a fenomeni macroscopici, in cui si ha la presenza di un gran numero di fotoni, dell’ordine di qualche milione, il trasporto di energia può essere considerato continuo.

Spettro delle radiazioni

Lo spettro delle radiazioni elettromagnetiche è molto ampio e si estende dalle onde hertziane ( limite inferiore ~10² Hz ) ai raggiche hanno frequenze superiori a 10¹⁸ Hz.

Si ricordi prima la relazione che intercorre fra la lunghezza d’onda e la frequenza :

( 1 )

dove è la velocità della luce, pari a 3·10⁸ m/s.

Lo spettro è convenzionalmente suddiviso in una successione di bande, di cui è fornita una descrizione in seguito, le cui separazioni non sono nette e gli intervalli possono avere zone di sovrapposizione, come accade per esempio alle alte frequenze tra raggi X e raggi.

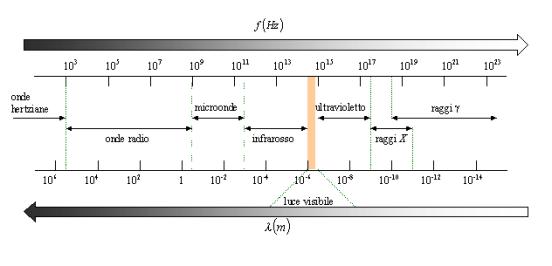
Figura 3; Spettro delle radiazioni.

Onde hertziane 50 1000 Hz , 10⁹ 10⁶ m

Le onde hertziane furono scoperte da Hertz, e si trovano alle maggiori lunghezza d’onda ed alle frequenze più basse.

Onde radio 10³ 10⁹ Hz , 10⁶ 0.3 m

Le onde radio sono utilizzate in prevalenza nelle trasmissioni radio ed, in particolare, per la telefonia cellulare.

Per quanto riguarda l’intervallo di frequenza si parte da poche migliaia di hertz ( le cosiddette onde radio lunghe ), fino ad arrivare a 1.8 ÷ 2 GHz, in applicazioni di telefonia cellulare, a cui corrispondono lunghezza d’onda di valore poco inferiore al metro.

Microonde 10⁹ 3 · 10¹¹ Hz , 0.3 10^-3 m

Le microonde sono utilizzate in prevalenza nelle applicazioni termiche, per esempio nei forni a microonde, oppure per comunicazioni e sistemi radar.

Il campo delle microonde parte da qualche decina di GHz, fino a 10¹¹ Hz, con lunghezza d’onda che arrivano fino al millimetro.

Infrarosso 3 · 10¹¹ 3.8 · 10¹⁴ Hz , 10^-3 0.78 · 10^-6 m

Le radiazioni infrarosse sono prodotte da corpi caldi, in cui gli atomi vengono eccitati tramite gli urti causati dall’agitazione termica. Se assorbiti da una molecola i quanti hanno un’energia sufficiente a provocare un moto vibrazionale, che si traduce in un aumento di temperatura.

L’emissione infrarossa è utilizzata in medicina per terapie fisiche e, nella ricerca, per lo studio dei livelli energetici vibrazionali delle molecole.

Luce visibile 3.8 · 10¹⁴ 7.9 · 10¹⁴ Hz , 0.78 · 10^-6 0.38 · 10^-6 m

Il campo della luce visibile è molto stretto rispetto all’intero spettro delle radiazioni, seppure sia molto importante per gli organismi viventi, poiché l’occhio della maggior parte di essi è sensibile a queste radiazioni.

Il sole è la più importante sorgente di luce visibile; l’energia elettromagnetica ha origine dall’agitazione termica degli atomi che si trovano sulla superficie ad una temperatura di 6000K.

Lo spettro della radiazione solare è il seguente:

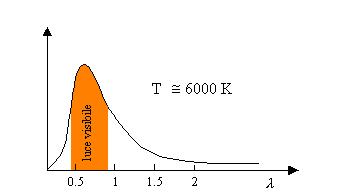
Figura 4; Spettro solare.

Colori della luce visibile:

Colore	f ( 10^14 Hz )	l ( 10^-6 m )
Rosso	3.85 – 4.82	0.780 – 0.622
Arancione	4.82 – 5.03	0.622 – 0.597
Giallo	5.03 – 5.20	0.597 – 0.577
Verde	5.20 – 6.10	0.577 – 0.492
Azzurro	6.10 – 6.59	0.492 – 0.455
Violetto	6.59 – 7.89	0.455 – 0.380

Ultravioletto 7.9 · 10¹⁴ 5 · 10¹⁷ Hz , 0.38 · 10^-6 6 · 10^-10 m

Le principali sorgenti di onde ultraviolette sono: il sole, i fulmini ( seppure per breve tempo ) e l’arco delle saldatrici elettriche.

Una parte notevole delle radiazioni ultraviolette prodotte dal sole sono assorbite dall’atmosfera, provocando la reazione di formazione dell’ozono O₃. Tale assorbimento è fondamentale per la vita sulla terra, in quanto questa radiazione in grandi quantità risulta letale. È noto a tutti il problema dell’assottigliamento dello strato di ozono dovuto principalmente ai clorofluorocarburi ( CFC ).

Tanto più i raggi ultravioletti sono ad alta frequenza, tanto più sono dannosi per gli esseri viventi; non tanto perché aumenta il loro potere penetrante nei tessuti, tanto più perché si avvicina a valori di lunghezza d’onda che mandano in risonanza i legami molecolari, portandoli alla rottura.

Il principale utilizzo delle radiazioni ultraviolette è la sterilizzazione.

Raggi X 5 · 10¹⁷ 5 · 10¹⁹ Hz , 6 · 10^-10 6 · 10^-12 m

Il loro principale utilizzo è in campo medico. Il loro potere penetrante è molto elevato, tanto da poter attraversare il corpo umano ed arrivare agli organi interni. L’assorbimento dei raggi X è differente nei tessuti del corpo umano e soprattutto nelle ossa; il flusso di raggi X che attraversa il corpo è quindi diverso in corrispondenza del tessuto attraversato e una lastra fotografica viene più o meno impressionata.

Grazie alla loro grande quantità di energia, i fotoni X sono in grado di distruggere i tessuti.

Raggi g 3 · 10¹⁸ Hz , 10^-10 m

Queste radiazioni sono tipiche dei raggi cosmici, ma non arrivano fino alla superficie terrestre perché filtrati prima dall’atmosfera.

Sono inoltre estremamente dannose per le cellule umane, in quanto portano alla rottura delle strutture molecolari. Una prolungata esposizione ai raggi g, dovuta a reazione nucleare, può essere letale anche se è basso il trasporto di energia.

Le radiazioni ultraviolette, raggi X e raggi g, sono dette radiazioni ionizzanti, poiché anche con piccole dosi di energia, sono in grado di rompere i legami molecolari e di ricombinarli. Per queste onde non deve essere trascurato l’effetto termico, ma è predominante l’effetto dannoso sugli esseri viventi.

Gli aspetti termici sono maggiormente considerati nel campo delle microonde, infrarosso e visibile, mentre per le onde radio questo aspetto è quasi trascurato. A basse frequenze invece il campo magnetico diventa predominante rispetto al trasporto di energia.

In questa sede ci si limiterà a considerare gli effetti termici dovuti alle microonde, infrarosso e visibile.

Quantità di energia emessa da un corpo

Un corpo, che si trova ad una certa temperatura T, è in grado di emettere energia E per irraggiamento,cioè scambiare calore senza dover essere a contatto con altro corpo, anche in presenza del vuoto. Ogni corpo è in grado di emettere o assorbire una quantità di energia in ogni direzione, che varia in funzione della sua temperatura e della sua conformazione.

Ne esistono alcuni che emettono una quantità di energia massima, oltre la quale nessun corpo ne sprigiona di più, tali corpi sono detti corpi neri.

Questa definizione è proprio legata al suo colore, poiché in funzione di essa varia la sua emissività.

Se si considerano due corpi, una certa quantità di calore verrà trasmessa mediante irraggiamento all’altro corpo e viceversa. Di norma il calore scambiato nelle due direzioni non è uguale, poiché il corpo più caldo irraggia più calore.

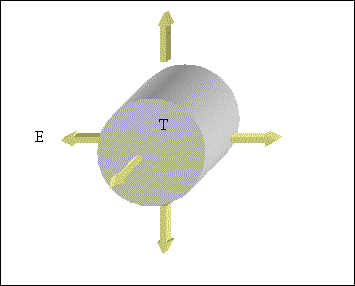
Figura 5; Emissione di energia per un corpo a temperatura T.

Se consideriamo lo spettro dell’emissione di un corpo qualsiasi, ad una certa temperatura T, si presenta frastagliato, cioè per certi valori di lunghezza d’onda si presenta un picco di emissione di energia, mentre per altri si hanno valori molto bassi di emissione.

Presi due corpi differenti anche alla stessa temperatura T, possono presentare due spettri molto differenti fra loro, come mostrato in figura 6 ( i due spettri sono rappresentati in rosso e blu ).

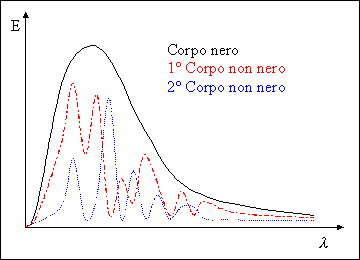
Figura 6; Spettro di un corpo nero e di due corpi qualsiasi a temperatura T.

Se si svolge l’inviluppo delle righe di emissione di infiniti corpi diversi ad una stessa temperatura T, si ottiene la curva caratteristica del corpo nero. Tale curva rappresenta il valore massimo di emissione relativo ad ogni frequenza a cui un corpo può arrivare.

Il corpo nero è quindi un’astrazione, poiché non può esistere rigorosamente in natura, anche se in laboratorio è possibile ricostruire un oggetto la cui caratteristica di emissività si avvicina a quella di un corpo nero.

Tale oggetto deve essere concavo, con una piccola cavità interna, di colore scuro (quasi nero), realizzato con materiale scabro ed opaco.

Figura 7; Possibile sezione di un corpo nero.

La cavità del corpo rappresentato in figura 7 si avvicina ad avere le emissioni di un corpo nero, perché le radiazioni entrano facilmente e si disperdono poi all’interno del materiale, rendendo praticamente trascurabili le radiazioni uscenti.

Si usa dare anche un’altra definizione di corpo nero, diametralmente opposta alla precedente, definendolo come quel corpo che assorba totalmente un’onda ad ogni frequenza, senza rifletterla.

Se consideriamo l’analogia con il campo sonoro, un’onda incidente che colpisce un materiale, di intensità I_i, si scompone in una parte che attraversa il corpo, detta onda assorbita, di intensità I_a, ed in un’altra che viene respinta, detta onda riflessa, di intensità I_a.

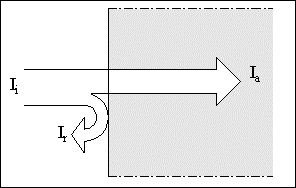
Figura 8; Scomposizione di un'onda che incide un materiale.

Per un corpo nero si ha che il coefficiente di assorbimento a, definito come :

( 2 )

ed il coefficiente di riflessione, definito come :

( 3 )

sono rispettivamente a = 1 e r = 0, cioè si ha un assorbimento totale, mentre è nulla la riflessione ad ogni frequenza.

Gli altri corpi sono detti colorati, cioè hanno differenti valori di riflessione e di assorbimento per valori di frequenza diversi. Ciò causa la riflessione per determinati valori di frequenza, ed un alto assorbimento per le altre, causando il colore del materiale.

Per esempio un corpo verde ha un’elevata riflessione per valori di lunghezza d’onda caratteristici del verde, mentre ha un elevato assorbimento alle altre lunghezze d’onda.

Leggi del corpo nero

Tali leggi valgono solamente per il corpo nero e sono di norma più semplici rispetto a leggi che riguardano anche altri corpi.

La maggior parte dei corpi non sono assimilabili al corpo nero, anzi le superfici metalliche si comportano di norma come superfici riflettenti e quindi poco assorbenti, così come le superfici alettate, che devono dissipare calore tramite irraggiamento.

Definizione di grandezze per l’irraggiamento

1) Potere emissivo integrale:

Per il trasporto di energia la quantità utilizzata normalmente non è l’intensità, come nel campo acustico, ma è il potere emissivo integrale, indicato con la lettera ‘’, la cui unità di misura è il Watt su metro al quadrato.

( 4 )

Il potere emissivo integrale dipende dalla conformazione di un corpo, in particolare dipende dalla sua superficie, e dalla sua temperatura. Il valore che assume rappresenta la quantità di energia che viene irradiata da un elemento di superficie unitario.

Si supponga di avere un corpo di forma qualsiasi, anche complessa, e di prendere un elemento unitario S di superficie, che irraggia una quantità di energia E in un tempo . Il potere emissivo integrale è quindi ridefinito come:

( 5 )

Il potere emissivo integrale per un corpo nero è il maggiore fra quelli emessi da tutti gli altri corpi.

2) Emissività:

L’emissività è definita come il rapporto fra e :

( 6 )

Per un corpo nero l’emissività è pari ad 1, mentre per un corpo non nero essa è sempre inferiore ad 1.

3) Potere emissivo specifico ( monocromatico )

Il potere emissivo monocromatico è definito come la derivata del potere emissivo integrale rispetto alla lunghezza d’onda.

( 7 )

è possibile stabilire una relazione fra il potere emissivo integrale e quello monocromatico:

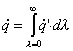( 8 )

4) Emissività monocromatica

Per un corpo non nero lo spettro risulta essere frastagliato; per certe lunghezze d’onda sarà possibile arrivare quasi fino a valori tipici del corpo nero, ma per altre lunghezze d’onda il corpo non nero presenta valori di emissione molto inferiori, come mostrato in figura 6.

Per tale motivo si ha la definizione di emissività monocromatica, oltre a quella definita in precedenza, data da il rapporto fra il potere emissivo monocromatico di un corpo qualsiasi e quello di un corpo nero.

( 9 )

Per il corpo nero l’emissività monocromatica è pari ad 1 per ogni valore di frequenza, per un corpo colorato ha un valore che può variare per ogni valore di lunghezza d’onda ( si veda la figura 10 ).

Legge di Stefan - Boltzmann

Tale legge definisce il quantitativo di energia complessiva emessa da un corpo nero.

( 10 )

dove è la costante di Stefan - Boltzmann tipica del corpo nero, il cui valore è e T è temperatura assoluta del corpo.

Nota: il pedice 0 riferito alle grandezze fisiche indica che esse sono riferite ad un corpo nero.

Legge di Wien

Lo spettro di un corpo nero assume una particolare forma ad ogni valore di temperatura, e per un certo valore di lunghezza d’onda detta , presenta un massimo, detto , come mostrato in figura 9.

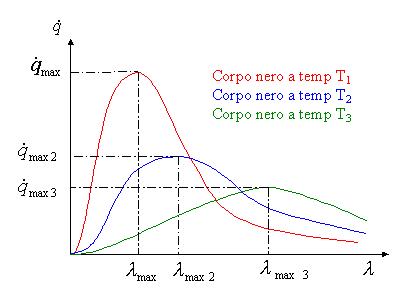
Figura 9; Spettro di corpi neri a differente temperatura.

Se si considera lo stesso spettro ad una temperatura T₂, tale che T₂ sia inferiore a T₁, cresce il valore della lunghezza d’onda, detto , per cui si verifica la massima emissione di energia. Lo stesso discorso vale se consideriamo una temperatura T₃ inferiore a T₂.

La relazione che si ha fra la diminuzione di temperatura e l’aumento di lunghezza d’onda è rappresentato dalla legge di Wien ( o legge del regresso ):

costante ( 11 )

cioè il prodotto fra la lunghezza d’onda e la temperatura si mantiene costante, ed il grafico di in funzione di T è un’iperbole.

Legge di Planck

La legge precedente indica, in base alla temperatura, il valore di lunghezza d’onda per cui si ha un massimo di emissione, ma non determina quanto vale il massimo valore di potere emissivo integrale. Tale valore è calcolato tramite la legge di Planck:

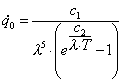( 12 )

dove c₁ e c₂ sono due costanti, dette costanti di Plance, di valore:

Tale legge fornisce la forma dello spettro di un corpo nero. Più la temperatura è alta, più il picco è alto e ben marcato e si trova in corrispondenza di lunghezze d’onda molto più piccole ( si veda la figura 9 ).

Legge di Prevost

La legge di Prevost è molto semplice, in quanto asserisce che la quantità di calore scambiata è pari a quella emessa meno quella ricevuta .

( 13 )

Poiché la quantità di calore ricevuta varia in funzione della capacità del corpo di assorbire energia, essa può essere definita come:

( 14 )

dove a è il coefficiente di assorbimento e è la quantità di calore incidente.

Per cui la legge ( 13 ) diventa:

( 15 )

Per esempio, se si considera la radiazione solare, pari a , che colpisce un corpo nero ( con a = 1 ) allora tutta l’energia verrà assorbita; se invece viene colpito un foglio di alluminio ( con a = 0.05 ) ne verrà assorbita il 5% della radiazione solare.

Il corpo grigio

Nelle applicazioni tecniche si sa che per la maggioranza dei casi i corpi non sono neri, ma molti di essi possono essere assimilabili a corpi grigi.

Il valore di assorbimento a per tali corpi non vale 1 come per i corpi neri, ma è inferiore, compreso fra 0 ed 1, e costante per ogni valore di lunghezza d’onda, a differenza dei corpi colorati. La stessa considerazione può essere fatta per il valore di emissività monocromatica .

Per tali motivi è possibile affermare che il corpo grigio è un corpo nero che ha un valore di assorbimento e di emissione inferiore, ma costante al variare della frequenza.

Il comportamento di un corpo grigio è possibile ricondurlo a quello di un corpo nero semplicemente moltiplicando il valore ottenuto per l’emissività monocromatica, il cui grafico è mostrato in seguito:

Figura 10; Emissività monocromatica per corpi differenti.

è possibile anche utilizzare l’emissività integrale al posto dell’emissività monocromatica, poiché per il corpo grigio essa è costante per ogni lunghezza d’onda.

Per il corpo grigio la legge di Stefan – Boltzmann diventa:

( 16 )

In tale modo, poiché il valore di < 1 , il valore di potere emissivo integrale è inferiore a quella del corpo nero.

Potere emissivo angolare e legge di Lambert

La legge di Lambert descrive il comportamento angolare di un materiale. Se per esempio si considera il caso più semplice, cioè una superficie piana, ci si potrebbe aspettare un’emissione uniforme diretta in ogni direzione, ma ciò non avviene.

Per calcolare il potere emissivo in una direzione, si consideri il vettore normale alla superficie, e si determini il vettore potere emissivo in ogni direzione.

Si può così constatare che il vettore non ha lo stesso valore in ogni direzione, ma tanto più si allontana dal vettore normale, tanto più diminuisce, come mostrato in figura 11.

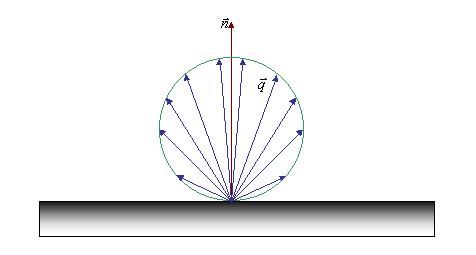
Figura 11; Comportamento del potere emissivo.

In particolare la legge di Lambert definisce il potere angolare i, dato da:

( 17 )

dove è l’angolo solido, come indicato in figura 12.

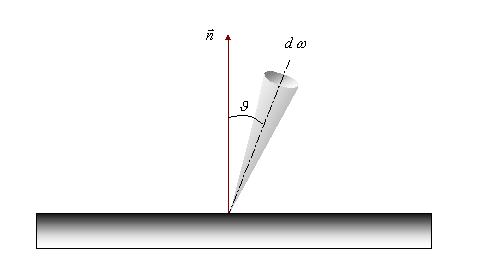
Figura 12; Rappresentazione dell’angolo e .

Dalla relazione ( 17 ) si può ricavare:

( 18 )

dove è l’angolo, espresso in steradianti, formato dalla superficie piana che irraggia da un solo piano.

Definizione di steradiante:

Un angolo espresso in radianti è dato dal rapporto fra l’arco ed il raggio, come mostrato in figura 13.1.

( 19 )

Per definizione un radiante è l’angolo che ha un arco pari al raggio.

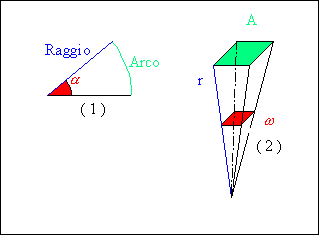
Figura 13; Angolo piano e solido.

La definizione di steradiante è simile alla precedente, ma, invece dell’angolo piano, ci si riferisce all’angolo solido.

Si prenda in considerazione un solido di raggio r e di area sottesa A, come mostrato in figura 13.2.

L’angolo solido è dato da :

( 20 )

Lo steradiante è quindi quell’angolo solido che ha per superficie sottesa un’area pari al raggio al quadrato.

L’intera sfera, che ha una superficie esterna di , ha un angolo al centro di steradianti, mentre la superficie piana ha un angolo di steradianti.

La legge di Lambert descrive l’andamento angolare di i in funzione dell’angolo , che rappresenta l’allontanamento dal vettore normale alla superficie, come mostrato in figura 12.

( 21 )

dove i_n è il massimo valore di potere emissivo angolare ottenuto in corrispondenza della normale .

I vettori di i ( in blu nella figura 14 ) non sono quindi uniformi, ma il loro valore cala con la legge del coseno, ed in corrispondenza della tangente alla superficie, cioè per , è nullo. L’inviluppo totale è quindi descritto da una circonferenza.

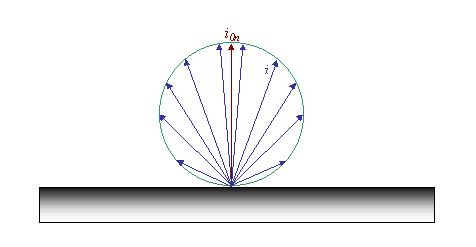
Figura 14; Comportamento del potere angolare i.

Se il corpo avesse un’emissione angolare uniforme in ogni direzione, l’inviluppo sarebbe una semicirconferenza, come mostrato in figura 15, ed il vettore i sarebbe costante e pari a , cioè la metà del valore massimo del potere emissivo integrale ottenuto da un corpo nero.

Nella realtà è più probabile trovare superfici che emettono radiazioni in modo uniforme e quindi con i costante.

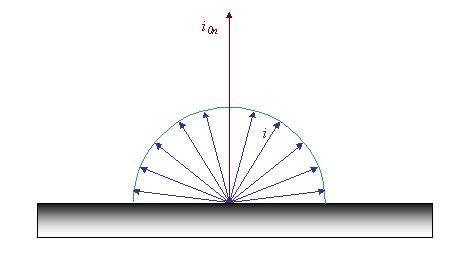
Figura 15; Comportamento del potere angolare i per un'emissione uniforme.

è necessario ricordare che tale legge vale solo per i corpi neri. Per i corpi colorati gli inviluppi dei vettori non sono delle circonferenze, ma assumono delle forme irregolari, in funzione del materiale e della superficie.

Il comportamento della superficie di un corpo nero può essere paragonato a quello di un corpo grigio, che ha potere emissivo monocromatico inferiore rispetto al corpo nero, ma costante al variare della lunghezza d’onda.

Un corpo grigio è detto lambertiano se i vettori i mantengono lo stesso inviluppo del corpo nero ed il suo potere emissivo integrale è pari a :

( 22 )

Coincidenza fra effetti emissivi ed effetti assorbitivi

È necessario ora dimostrare la relazione che intercorre tra effetti emissivi ed effetti assorbitivi.

Ciò è reso possibile utilizzando una cavità isoterma, mantenuta alla stessa temperatura T, e ponendo all’interno una piccola lastra di materiale con temperatura differente dalla cavità, come mostrato in figura 16.

Figura 16; Cavità isoterma a temperatura T .

A regime, dopo un certo tempo, la lastra si porterà alla temperatura T della cavità. Ciò significa che la quantità di calore emessa dalla lastra è uguale alla quantità di calore ricevuta.

Tale considerazione vale anche se la cavità non è un corpo nero, in tal caso la lastra si raffredderebbe emettendo calore in modo differente ad ogni lunghezza d’onda.

In conclusione tanta energia viene erogata dalla lastra, tanta ne viene assorbita per ogni valore di . In caso contrario se ne fosse emessa meno di quanta assorbita la lastra si riporterebbe ad una temperatura superiore di T .

Se la lastra è un corpo grigio si ha che l’emissività specifica è pari al coefficiente di assorbimento:

( 23 )

Quindi se per il corpo grigio = 0.7, anche il coefficiente di assorbimento della lastra vale 0.7.

Per un corpo colorato si ha che:

( 24 )

cioè i valori dell’emissività specifica e del coefficiente di assorbimento sono uguali solo per certi valori di lunghezza d’onda.

Temperatura di colore

Secondo la legge di Wien più aumenta la temperatura, più la lunghezza d’onda, per cui si ha un massimo di energia emessa, assume valori minori all’interno dell’intervallo del visibile, a cui corrispondono valori colori tipici del violetto; viceversa se decresce la temperatura, la lunghezza d’onda assume valori tipici del colore rosso.

Figura 17; Spettro del visibile e temperatura di colore.

Nasce così la possibilità di associare il colore dello spettro visibile alla temperatura, detta temperatura di colore.

A basse temperature si associa il colore rosso, mentre ad alte temperature si associa un colore violetto. Ciò può sembrare un paradosso, se posto in relazione con la normale concezione dei colori, che ad un colore caldo associa il rosso, mentre ad uno freddo il violetto.

Definiamo ora alcune temperature di colore per differenti tipi di illuminazione:

	Temperatura di colore
Lampada incandescente	3500 k
Tubo fluorescente	7000 k
Xeno	5500 k
Sole	6000 k

Lo xeno utilizzato nelle lampade a scarica di gas e nelle macchine fotografiche, ha una temperatura di colore simile a quella solare. Quindi se in un ambiente esterno, illuminato da luce solare, si utilizza una macchina fotografica con flash allo xeno, i colori della foto rimangono naturali, poiché sia lo xeno che la radiazione solare hanno la stessa temperatura di colore.

Se invece si utilizza la stessa pellicola e lo stesso flash in un ambiente chiuso con luce prodotta da un tubo fluorescente, verranno esaltati maggiormente i colori freddi azzurri - viola, poiché il tubo fluorescente ha una temperatura di colore maggiore di quella solare. Se l’ambiente invece è illuminato con lampada incandescente, che ha una temperatura di colore più bassa di quella solare, saranno messi in risalto i colori caldi, in particolare il rosso.

Per l’occhio umano non si ha una predominanza di certi colori in base al tipo di illuminazione dell’ambiente, perché dopo un certo tempo, l’occhio umano compensa la scarsità di certi colori e l’esaltazione di altri, adattandosi in modo automatico.

Anche le ultime telecamere sono in grado di effettuare un bilanciamento del bianco automatico, cioè una stima dello spettro luminoso del luogo che si sta filmando, compensando i colori che sono meno predominanti in quel determinato ambiente.

Le vecchie telecamere analogiche dovevano essere invece calibrate in modo manuale, puntando verso un muro bianco o utilizzando un tappo bianco montato sull’obiettivo ed effettuando poi il bilanciamento del bianco, per avere una ripresa con colori il più possibile naturali.

Per gli ambienti chiusi, secondo disposizioni di legge, non è sufficiente garantire un’adeguata illuminazione fornendo una certa energia luminosa ( per le aule scolastiche tale energia deve essere almeno di 200 W/m² ), ma è necessario garantire una certa qualità spettrale della luce.

Normalmente utilizzata in ambiti scolastici e lavorativi, la luce dei tubi fluorescenti, in cui si ha una predominanza dei colori freddi, è sgradevole per la vista umana, poiché la affatica, e non favorisce la concentrazione.

In effetti le leggi sono orientate a definire dei requisiti a cui gli ambienti pubblici devono sottostare, in particolare il D.M. del 1975 fornisce delle norme, oltre che in campo acustico, anche in campo di illuminazione: è necessario favorire la corretta illuminazione dall’esterno e la temperatura di colore del sistema di illuminazione deve essere di circa 5500 K, cioè un valore simile a quello ottimale della luce solare.