PROPRIETA’ DELLE SOSTANZE PURE

 

 

Introduzione

In questa lezione si prenderanno in esame le proprietà delle sostanze pure. Ogni sostanza è caratterizzata da stati di aggregazione (detti anche fasi) dipendenti dalle condizioni termodinamiche, cioè dai valori di pressione, volume e temperatura della sostanza stessa.  Le fasi sono caratterizzate da alcune proprietà:

 

·        Fase solida	È caratterizzata da forma e volume propri, infatti le forze intermolecolari sono talmente forti da determinare una struttura cristallina che ingabbia le molecole in posizioni ben determinate (es: cloruro di sodio).
·        Fase liquida	È caratterizzata da volume proprio e forma variabile, infatti le forze intermolecolari hanno intensità minore rispetto alla fase solida; tale intensità non è sufficiente a conferire una forma propria alla sostanza che, perciò, assume la forma del recipiente in cui è contenuta (es: bicchiere d’acqua).
·        Fase aeriforme	È caratterizzata da volume e forma variabili, infatti le forze intermolecolari sono talmente deboli (la minore intensità fra le tre fasi) da non poter vincere l’agitazione termica delle molecole; la sostanza tende ad occupare il maggior volume possibile, perciò la forma ed il volume sono imposte dal contenitore (es: bombola di metano). In genere si distinguono in gas e vapori a seconda delle condizioni termodinamiche.

 

Per determinare le condizioni termodinamiche di una sostanza pura in un determinato stato di aggregazione, si fa riferimento al diagramma p-v-T (detto anche diagramma collinare) della sostanza (figura. 1).

 

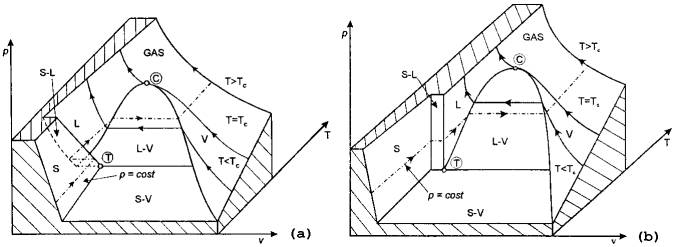
Figura 1: Diagramma collinare per una sostanza che si comporta come l'acqua (a) o come gli idrocarburi (b).

Il diagramma collinare è la rappresentazione tridimensionale della funzione , perciò rappresenta una superficie, non un volume. Nel grafico sono indicate le lettere relative allo stato di aggregazione: Liquido, Solido, Vapore e GAS.

Si può osservare che i due grafici collinari differiscono nel tratto della solidificazione (o fusione , dipendentemente dal senso della trasformazione). Le sostanze che, come l’acqua, aumentano di volume solidificando, hanno la regione S-L come quella del grafico (a); le sostanze che, come gli idrocarburi, diminuiscono di volume solidificando, hanno la regione S-L come nel grafico (b).

Si può osservare che, definite due coordinate termodinamiche, è sempre determinata la terza. Questa proprietà deriva immediatamente dalla regola delle fasi (o regola di Gibs):

 

               (1)

 

dove:

V è la varianza, il parametro che esprime il numero di coordinate indipendenti;

C è il numero di componenti (o sostanze);

F è il numero di fasi contemporaneamente presenti.

Questa regola è stata enunciata per sistemi aperti dove la massa è variabile, perciò C deve essere variabile; nel nostro caso, facendo riferimento a sistemi chiusi, dove la massa non varia, C è costantemente unitario, poiché nel sistema può esserci solo quella particolare sostanza studiata.

Applicata al diagramma tridimensionale si può osservare che se è presente un unico stato di aggregazione () si ottiene , cioè è possibile variare solo due coordinate termodinamiche e la terza è univocamente determinata; se sono presenti due stati di aggregazione contemporaneamente () si ottiene , cioè è possibile variare una unica coordinata e le altre due sono univocamente determinate; se sono presenti tutti e tre gli stati () si ottiene , cioè la condizione è determinata da una terna di valori ben precisi.

Da questo diagramma è possibile ricavare il diagramma p-v ed il diagramma p-T: è sufficiente intersecare il diagramma tridimensionale con dei piani “isotermici” e “isocori” rispettivamente.

 

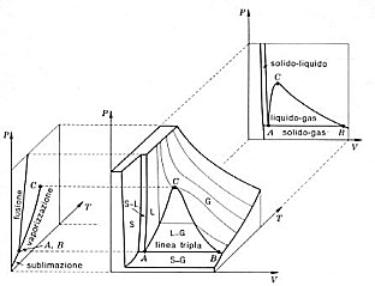
Figura 2: costruzione dei diagrammi p-v e p-T da quello collinare.

 

Da ognuno di questi è possibile trarre informazioni importanti sul comportamento della sostanza.

 

 

Diagramma p-v.

 

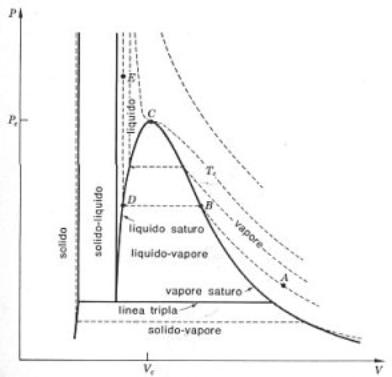
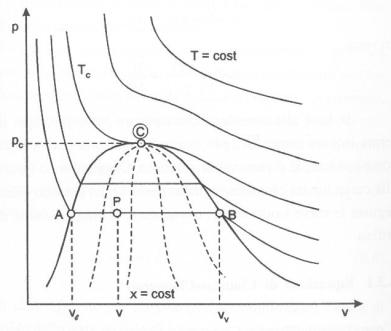
Figura 3: Diagramma p-v per una sostanza pura e curve isotitolo della miscela liquido-vapore.

 

Il diagramma p-v rappresenta una famiglia di caratteristiche isotermiche, cioè ogni curva rappresenta l’intersezione fra il diagramma collinare ed un piano a , perciò ogni linea rappresenta una trasformazione isotermica.

Se si introduce  d’acqua a circa  in un recipiente di circa  di volume in cui è stato fatto preventivamente il vuoto, l’acqua evaporerà completamente e il sistema si troverà nella condizione di vapore surriscaldato. Sul diagramma p-v di fig. 3, questo stato è rappresentato, ad esempio, dal punto A. Se ora il vapore viene compresso, a temperatura costante, la pressione aumenterà fino a che, nel punto B, non si abbia vapore saturo. Se si seguita a comprimere, il vapore condensa, mentre la pressione, se non si varia la temperatura, rimane costante.  Il segmento rettilineo BD rappresenta la condensazione isobara ed isoterma di vapor d’acqua; il valore costante che la pressione mantiene durante questo processo prende il nome di tensione di vapore. In ogni punto del segmento BD c’è equilibrio fra acqua e vapor d’acqua, mentre, nello stato rappresentato dal punto D si ha solo liquido saturo. Poiché per comprimere l’acqua liquida serve un forte aumento di pressione, la linea DE, che rappresenta gli stati del liquido compresso, è pressoché verticale. In ogni punto della linea DE l’acqua si trova nella fase liquida L; in ogni punto della linea AB nella fase di vapore V; in ogni punto del segmento BD c’è equilibrio fra fase liquida e fase di vapore L-V. La curva ABDE mostra l’andamento tipico, in un diagramma p-v, delle isoterme di una sostanza pura.

A temperature diverse, le isoterme hanno andamenti simili, come mostrato dalle curve tratteggiate di fig. 3. Si noti che i segmenti che rappresentano gli stati in cui c’è equilibrio fra liquido e vapore, le cosiddette linee di vaporizzazione, diventano sempre più corte a mano a mano che la temperatura aumenta, fino a che non si raggiunge la temperatura critica , al di sopra della quale non c’è più distinzione fra liquido e vapore. L’isoterma alla temperatura critica si chiama isoterma critica e il punto C, che costituisce il limite delle linee di vaporizzazione, si chiama punto critico. Si nota che l’isoterma critica presenta nel punto critico un flesso orizzontale. La pressione ed il volume corrispondenti al punto critico si chiamano pressione critica  e volume critico . Tutti i punti che rappresentano stati in cui si ha liquido saturo, giacciono sulla cosiddetta curva di saturazione del liquido, mentre i punti rappresentativi del vapore saturo, giacciono sulla cosiddetta curva di saturazione del vapore. Queste due curve si incontrano nel punto critico, al di sopra del quale le isoterme sono rappresentate da curve continue che, per grandi valori del volume e piccoli valori della pressione, approssimano le isoterme di un gas ideale.

Nel diagramma di fig. 3 compaiono anche le zone di equilibrio S-L e S-V. Le isoterme che attraversano la zona S-V hanno lo stesso andamento di quelle a temperatura più alta. Il tratto di isoterma orizzontale rappresenta, in questo caso, la transizione del solido saturo al vapore saturo, cioè la sublimazione. Esisterà, evidentemente una curva che separa L-V dalla zona S-V. Tale linea è in relazione col punto triplo (T in fig. 1, A in fig. 2) ed è detta linea tripla.

La curva contenente la regione L-V è detta curva limite o curva di Andrews. Un parametro estremamente importante per queste miscele è il titolo (x) della miscela che è definito come:

 

               (2)

 

dove  è la massa del vapore e  è la massa del liquido. Avendo a che fare con sistemi chiusi, in cui la massa totale della sostanza non cambia, in ogni punto del segmento BD la quantità  è la massa totale di sostanza considerata; il titolo indica, perciò, la quantità di vapore riferita al totale presente in ogni punto del segmento orizzontale. Una proprietà, discendente direttamente da queste osservazioni, è la proprietà di tracciare delle curve isotitolo che uniscono tutti i punti all’interno della curva limite aventi il medesimo valore di titolo. Si può dimostrare che esiste una proporzionalità fra la lunghezza del segmento ed il valore del titolo: se si considera, ad esempio, , la curva isotitolo passerà per il punto mediano di tutti i segmenti. Analogamente si può concludere che la curva del liquido saturo è la curva isotitolo e che la curva del vapore saturo è la curva isotitolo .

 

 

Diagramma p-T

 

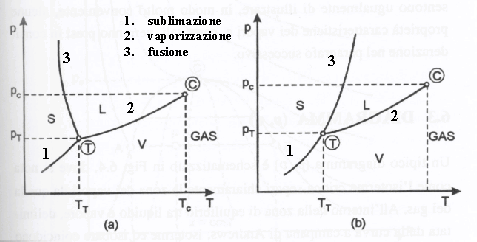
Figura 4: diagramma p-T per sostanze che si comportano come l’acqua (a) e per sostanze che si comportano come gli idrocarburi (b).

 

Il diagramma p-T si ottiene da quello collinare intersecondo quest’ultimo con un piano del tipo . Il risultato è un grafico come quelli di fig. 4.

Se si misura la tensione di vapore di un solido al variare della temperatura fino a che non si raggiunge il punto triplo, e poi quella del liquido fino a che non si raggiunge il punto critico, si ottiene un risultato che, riportato su un diagramma p-T, ha l’aspetto delle due curve più basse della figura 4. Il punto T è il punto triplo e C è il punto critico. Se si comprime la sostanza al punto triplo fino a che non c’è più vapore e poi si aumenta la pressione della miscela di liquido e solido, bisogna variare la temperatura se si vuole che liquido e solido  restino in equilibrio. Si ottengono cioè, sperimentalmente, tre curve:

1.      i punti che rappresentano stati in cui coesistono solido e vapore giacciono sulla curva di sublimazione;

2.      i punti che rappresentano stati in cui coesistono liquido e vapore giacciono sulla curva di vaporizzazione;

3.      i punti che rappresentano stati in cui coesistono liquido e solido giacciono sulla curva di fusione.

Nel caso particolare dell’acqua, la curva di sublimazione si chiama linea del gelo, quella di vaporizzazione linea del vapor d’acqua e quella di fusione linea del ghiaccio.

Qualunque sia la sostanza, le curve di vaporizzazione e sublimazione hanno pendenza positiva. La curva di fusione, invece, può avere pendenza positiva o negativa, anche se per la maggior parte delle sostanze la pendenza è positiva. Un’importante eccezione è costituita dall’acqua. Le sostanze che, come l’acqua, fondendo si contraggono, hanno una curva di fusione con pendenza negativa, mentre quelle che fondendo si dilatano, presentano curve di fusione con pendenza positiva. Il punto triplo è il punto di incontro delle curve di fusione, sublimazione e vaporizzazione. Solo in un diagramma p-T il punto triplo è effettivamente rappresentato da un punto; in un diagramma p-v esso è rappresentato da una linea. La tabella 1 raccoglie le coordinate dei punti triplo e critico di alcune sostanze.

 

Tabella 1: coordinate dei punti triplo e critico di alcune sostanze.

 

In un diagramma p-T i punti che rappresentano stati di equilibrio di una sola fase definiscono certe zone che sono limitate dalle varie curve di saturazione, cioè dagli insiemi di punti che rappresentano stati di equilibrio di due fasi. Così, nella figura 4, la zona del solido è limitata inferiormente dalla curva di sublimazione e a destra dalla curva di fusione. Questa divisione in zone è in certa misura arbitraria per le fasi limitate dalla curva di vaporizzazione, che termina al punto C. Convenzionalmente si adottano come limiti della zona del liquido la curva di fusione, la curva di vaporizzazione e l’isoterma critica (rappresentata, in figura 4, dalla retta verticale tratteggiata). La zona del vapore è limitata dalla curva di sublimazione, dalla curva di vaporizzazione e dall’isoterma critica; questo significa che un vapore può venire condensato diminuendo la temperatura o aumentando la pressione. La zona del gas comprende, oltre alla zona del vapore, quegli stati per cui  e . Un gas può venire sempre condensato diminuendo la temperatura, ma non sempre aumentando la pressione. Per  e  non si può stabilire una netta distinzione fra gas e liquido; perciò, generalmente questa zona è detta zona del fluido.

 

Gas perfetti

I gas rappresentano le sostanze termometriche più convenienti, in virtù del fatto che il rapporto fra la pressione P del gas ad una certa temperatura e la pressione P_t dello stesso gas al punto triplo dell’acqua, tende a un valore costante indipendente dalla natura del gas al tendere di P e P_t a zero a volume costante

I gas vengono matematicamente modellati come:

·        gas ideali;

·        gas reali.

Il modello dei gas reali tiene conto del fatto che ogni gas è costituito da molecole aventi un determinato volume ed interagenti fra loro. Il volume delle molecole è da sottrarre al volume del sistema chiuso in cui è contenuto il gas; il fatto che tutte le molecole interagiscono fra loro, implica che esistano urti fra le molecole che vanno a modificare la pressione e la temperatura. Il modello dei gas ideali considera nullo il volume delle molecole e nulle le loro interazioni. Ovviamente nel mondo reale non esistono, a rigore, gas ideali, ma, in condizioni di bassissima pressione e grandissimo volume, è possibile considerare trascurabile il volume delle molecole rispetto a quello del sistema. E’ per questo che nei termometri a gas si utilizzano gas biatomici come l’ossigeno.

Nel diagramma collinare, quindi, i gas perfetti stanno nella regione di p basse, v alte e . In questa regione si ottiene un diagramma p-v come in figura 5.

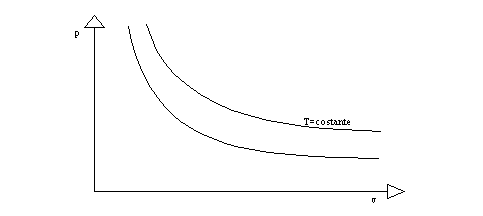
Figura 5: diagramma p-v dei gas perfetti.

 

L’equazione di stato, l’equazione che lega fra loro tutte le variabili termodinamiche, dei gas perfetti è:

 

               (2)

 

dove:

v è il volume specifico;

p è la pressione;

R è la costante dei gas perfetti;

T è la temperatura.

Questa la relazione in forma specifica. moltiplicando ambo i membri per la massa si ottiene la relazione in forma estensiva:

 

               (3)

 

Considerando la relazione:

 

               (4)

 

che lega il numero di moli della sostanza (n) alla massa (M) attraverso la massa molare (μ), si può riscrivere la (3), sostituendovi la relazione inversa della (4), ottenendo:

 

               (5)

 

Si pone, generalmente:

 

               (6)

 

Sostituendo la (6) nella (5) si ottiene:

 

               (7)

 

Considerando la relazione

 

               (8)

 

che lega il volume molare () al volume della sostanza attraverso il numero di moli, si può riscrivere la relazione (7) in questo modo:

 

               (9)

 

Le relazioni (2), (3), (7) e (9) sono equivalenti, perché sono la stessa equazione di stato dei gas perfetti espressa in modi diversi.

La massa molare (μ) è una costante dipendente solo dal gas e si può ricavare dalla tavola degli elementi. Due esempi sono:

 

 

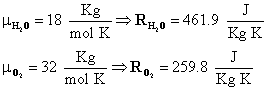
Si considerino ora i calori specifici. Essi sono definiti nel seguente modo:

 

               (10)

               (11)

 

Per i gas perfetti i calori specifici dipendono solo dalla temperatura, perciò le derivate parziali diventano derivate pure. Utilizzando il 1° principio della termodinamica applicato ad una trasformazione isobara ed una isocora ottengo:

 

               (12)

               (13)

 

e, sostituendo la (12) nella (10) e la (13) nella (11), si ottiene:

 

               (14)

               (15)

 

dalle quali si ottiene:

 

               (14)

               (15)

 

in cui si tiene conto del fatto che per ampi valori di temperatura il calore specifico è una costante.

Facendo le considerazioni analoghe per l’entropia si ottiene:

 

               (16)

 

Dal 1° principio applicato alle due trasformazioni si ottiene:

 

Trasformazione isobara:

               (17)

 

Trasformazione isocora:

               (18)

 

Sostituendo la (17) nella (16) e, successivamente, la (18) nella (16) ed utilizzando l’equazione di stato dei gas perfetti, si ottiene:

 

               (19)

               (20)

 

Prendendo un punto di riferimento a cui assegnare le coordinate , , , , , , le (14), (15), (19) e (20) si possono riscrivere nel seguente modo:

 

               (21)

               (22)

               (23)

               (24)

 

Si può ora considerare una trasformazione isoentropica in cui  (non è altro che una adiabatica reversibile). In questa condizione, facendo il rapporto membro a membro delle (23) e (24), si ottiene:

 

               (25)

 

Generalmente si indica:

 

               (26)

perciò l’equazione (25) si scrive:

 

               (27)

 

Si può dimostrare, utilizzando le (23) e (24) che:

 

               (28)

 

Le caratteristiche generali delle capacità termiche per i gas ideali sono molto semplici:

 

1.      tutti i gas:

·         è funzione solo di T;

·         è funzione solo di T ed è maggiore di ;

·        ;

·         è funzione solo di T ed è maggiore di 1.

 

2.      gas monoatomici come He, Ne, Ar e la maggior parte dei vapori metallici, come quelli di Na, Cd, Hg:

·         è costante su un ampio intervallo di T ed è molto prossimo a ;

·         è costante su un ampio intervallo di T ed è molto prossimo a ;

·         è costante su un ampio intervallo di T ed è molto prossimo a .

 

3.      gas biatomici cosiddetti permanenti, cioè H₂, O₂, N₂:

·        A T ordinarie  e  sono pressoché costanti, mentre a temperature più alte crescono lentamente;

·        A T ordinarie  è pressoché costante, mentre a temperature più alte decresce lentamente.

 

Si può notare che, sebbene  e  dipendano dalla sostanza, il loro rapporto tenda ad un valore costante che per gas biatomici è . Tanto più μ tende ad 1 tanto più la trasformazione assume carattere reversibile, perciò, dall’equazione (27), si ottiene una isoterma se la trasformazione è perfettamente reversibile.