INDICE:
PERDITE DI CARICO DISTRIBUITE
Le perdite distribuite costituiscono la base del calcolo dei fenomeni dissipativi nel moto dei fluidi.
Abbiamo visto che il diagramma di Moody viene utilizzato per valutare il fattore di attrito, però può anche essere utilizzato per il calcolo delle perdite localizzate:
il diagramma ci consente infatti di determinare il fattore di attrito x indispensabile per il calcolo della perdita di carico distribuita (che indicheremo con Rdist)
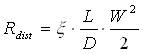
L = lunghezza, D = diametro, W = velocità media.
In generale il fattore di attrito x dipende da due parametri:
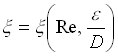
Il numero di Reynolds è un numero puro e ci dice se il moto è laminare o turbolento ed è dato dalla seguente relazione:
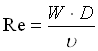
W = velocità media, D = diametro, n = velocità cinematica.
Mentre la scabrezza relativa ci dice se il tubo è più o meno liscio in altre parole è un fattore che dipende dalla possibilità che le pareti del tubo che stiamo considerando siano non lisce ma scabre, rugose.
Come già detto sopra la scabrezza relativa è data dal rapporto tra la rugosità e e il diametro del tubo misurato in millimetri.
DIAGRAMMA DI MOODY
Questo diagramma è realizzato in scala doppia logaritmica, in ascissa viene riportato il numero di Reynolds mentre in ordinata viene riportato il fattore d’attrito.
Viene diviso sostanzialmente in tre regioni:
Come si può vedere dal diagramma, il moto turbolento s’identifica con la parte di grafico al di sopra della linea tratteggiata, mentre il moto laminare è rappresentato dalla parte di grafico sottostante quella linea.
Questa linea tratteggiata separa la regione in cui il moto è laminare da quella in cui il moto è turbolento e rappresenta la regione di transizione.
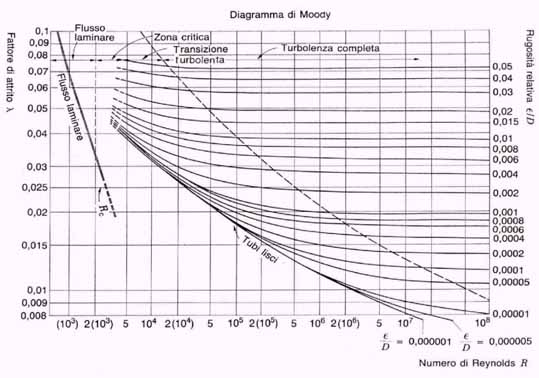
Si nota che nella regione che descrive il moto turbolento le curve sono orizzontali, questo ci fa capire che in questa regione non ho più dipendenza dal numero di Reynolds, quindi x è funzione solo della scabrezza relativa:
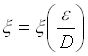
E facile quindi capire che al di sotto della linea tratteggiata (cioè per valori di Re più bassi) ho dipendenza da entrambi i parametri (Re e scabrezza relativa).
La curva più bassa di tutte rappresenta invece la curva del tubo liscio, la curva priva di scabrezza relativa.
Dal diagramma si vede quindi come all’inizio la scabrezza abbia importanza relativa ma al crescere del numero di Reynolds anche i valori di scabrezza estremamente modesti portano a spostamenti significativi rispetto al comportamento del tubo liscio, questo vuol dire che la scabrezza diventa il carattere dominante e il numero di Reynolds perde d’importanza.
Il numero di Reynolds è però molto importante in moto laminare dove la scabrezza non è significativa.
Dal diagramma si vede in oltre che la transizione tra moto laminare e moto turbolento viene fatta iniziare circa a 2000, in realtà il comportamento del moto laminare, che si dimostra analiticamente essere
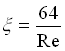
può essere esteso fino a 2500 – 3000.
Quindi se faccio crescere Reynolds lentamente partendo da una regione in cui il moto era laminare, mi rimane laminare fino a questo valore, se avanzo ancora mi trovo nella regione tratteggiata dove basta una minima perturbazione per far si che si passi alla regione di moto turbolento col rischio di non poter più tornare al moto laminare.
Per quanto riguarda le perdite si capisce che in regime laminare sono molto più piccole di quelle in regime turbolento quindi una volta che s’innesca una turbolenza s’innescano dei fenomeni dissipativi molto più forti di quelli che si avevano in regime laminare; quanto detto è però vero se io mi metto in regime di transizione cioè se considero i valori di Reynolds nei pressi della linea tratteggiata del diagramma.
Solitamente il moto laminare vale per fluidi viscosi come l’olio e la vaselina mentre per l’H2O e l’aria si usa il moto turbolento.
Se per errore mi trovassi in regime laminare e usassi le formule del regime turbolento, il diagramma ci direbbe che la turbolenza porterebbe all’aumento dei fenomeni dissipativi, in realtà però non è così perché la turbolenza aumenta i fenomeni dissipativi nel regime in cui effettivamente essa si sviluppa, ma se io estrapolo le curve trovo che il regime laminare ha delle perdite ancora superiori, quindi in poche parole non è un fattore di sicurezza usare formule del moto turbolento in regime laminare come non è un fattore di sicurezza usare formule del moto laminare in regime di turbolenza.
Tutto questo ci fa capire che è rischioso e non conveniente lavorare in regime di transizione visto che mi trovo a cavallo tra le due regioni (di moto laminare e di moto turbolento) e si rischierebbe quindi di capitare in una delle situazioni sopra descritte.
E’ quindi un regime instabile anche dal punto di vista fisico vediamo perché:
supponiamo che la velocità del flusso stia crescendo, entro in regime di transizione, s’innesca la turbolenza, allora le perdite crescono improvvisamente e quando ho più perdite il flusso tende a rallentare ma rallentando torna laminare, allora riprende ad accelerare perché le perdite sono più basse; quindi ho un regime instabile, s’innescano cioè fenomeni oscillatori e rumorosi che non si fermano più.
PERDITE DI CARICO CONCENTRATE
Sono causate dalla presenza lungo il condotto di una serie di accidentalità, vediamone alcuni esempi:
Le accidentalità più comuni sono comunque i convergenti e i divergenti sotto riportati (figure 2-3):
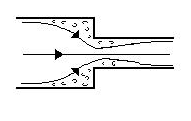
Figura 2: Esempio di accidentalità data da una convergenza
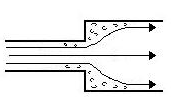
Figura 3: Esempio di accidentalità data da una divergenza
Esistono comunque delle tabelle che riportano queste accidentalità (figura 5):
in queste tabelle compare il simbolo rappresentante il tipo di accidentalità e affianco è presente un numero che mi rappresenta il coefficiente di perdita localizzata dato dalla seguente relazione:
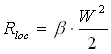
dove W rappresenta la velocità.
Come si può ben notare, in questa relazione non compare la lunghezza del condotto perché questa perdita è legata al tipo di asperità (alla brusca variazione di sezione) presente nel tubo.
Le perdite concentrate si vanno a sommare alle perdite distribuite viste in precedenza, facciamo un esempio:
consideriamo due tubi, uno di lunghezza L1 e diametro D1, l’altro di lunghezza L2 e diametro D2 e supponiamo che sia presente una perdita concentrata b , allora la perdita totale sarà data da:
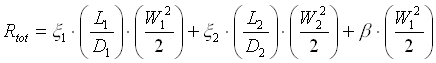
cioè è la somma della perdita distribuita nel primo tratto più la perdita distribuita nel secondo tratto più la perdita concentrata data dal restringimento della sezione
Graficamente avrei:
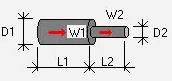
Figura 4
Il termine b si applica sempre alla velocità che c’è a monte dell’asperità, quindi in questo caso a W1.
Si capisce che passando da un tubo grande a un tubo piccolo la velocità cresce perché la portata deve rimanere costante.
Se la portata in massa nel punto è costante si avrà:
![]()
dove 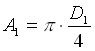 e
e 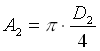
quindi se A2<A1 à W2 sarà proporzionalmente maggiore di W1.
La relazione scritta sopra prende il nome di equazione di continuità o equazione di bilancio della massa e ci da un legame tra la velocità presente nel tubo grande e la velocità presente nel tubo piccolo.
Dalla tabella di figura 5 si vede che il valore di b nel nostro caso è pari a 0.5, mentre per quanto riguarda i valori di x 1 x 2 in generale sono diversi perché essendo diversa la velocità e il diametro allora risultano diversi anche i momenti di Reynolds, devo quindi andare a ricercarli sul diagramma di Moody:
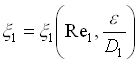 e
e 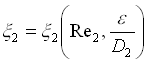
Si capisce che x 1 e x 2 dipendono sia da Reynolds che dalla scabrezza relativa.
Poiché questi tubi sono attaccati, la perdita totale è la somma delle perdite parziali come visto sopra.
Questi tubi si definiscono in serie.
Si comincia allora ad intravedere una certa analogia con i circuiti elettrici.
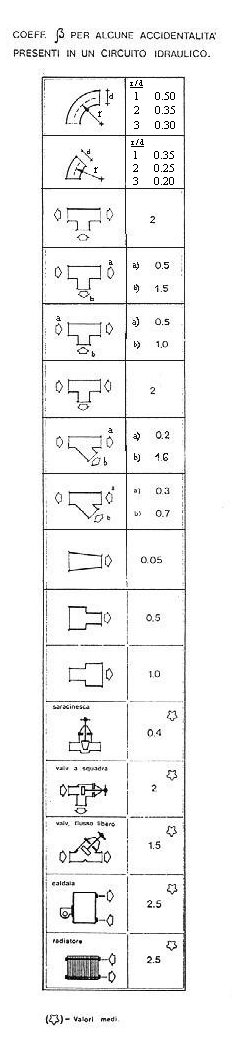 Figura 5
Figura 5
ANALOGIE CON L’ELETTROTECNICA
I tubi attaccati possono essere paragonati alla serie delle resistenze:
 è
è
è
è
è
è
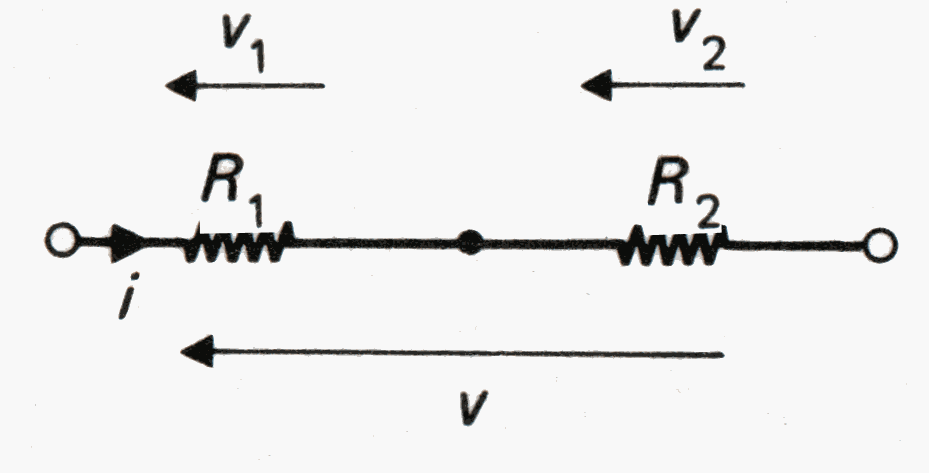
Figura 6
Se ho quindi due resistenze in serie, la resistenza equivalente (che indicheremo con Req) è data dalla somma delle due resistenze:
 è
è
è
è
è
è
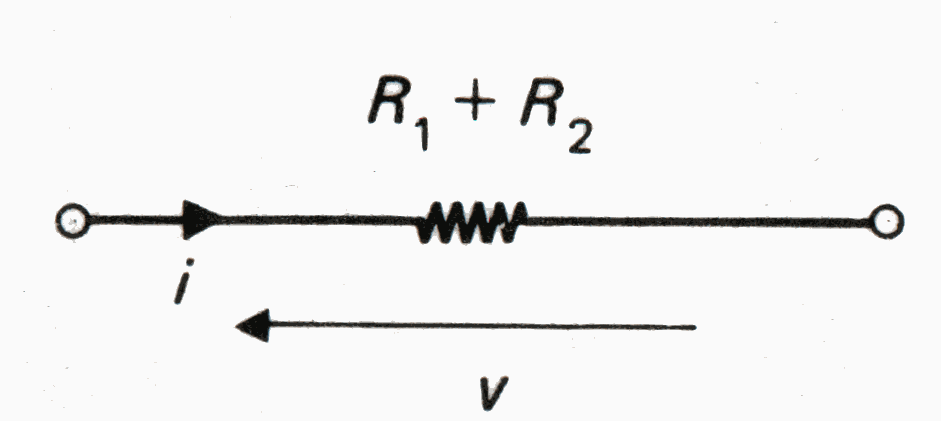
Figura 7
In oltre possiamo ancora notare che la tensione dei circuiti elettrici può essere paragonata alla presione del fluido ed in oltre la corrente che attraversa un circuito è rappresentata dalla portata del fluido che scorre nei condotti.
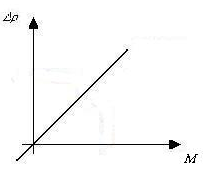
Abbiamo visto che un sistema in moto laminare ha una perdita di pressione che è proporzionale alla portata di fluido che vi scorre, cioè ha un andamento resistivo, ciò può essere paragonato ad un circuito elettrico puramente resistivo:
è è è
Figura 8
Supponiamo ora che affinchè funzioni, un circuito elettrico, abbia bisogno di un generatore elettrico che può essere rappresentato da una curva di questo tipo:
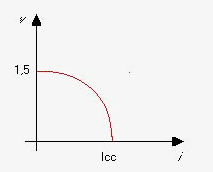
Figura 9
Si può pensare per esempio ad una pila che eroghi 1,5 V a vuoto.
Ogni pila ha una corrente massima ( Imax ) che chiameremo Icc (corrente di cortocircuito) ed è pari alla corrente ottenuta azzerando la d.d.p. (differenza di potenziale).
Allora la curva rappresentativa per il circuito elettrico è data da:
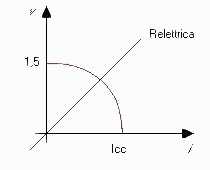 à
à
à
à
à
à
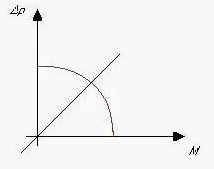
Figura 10
Come si può vedere dalla figura 10 (secondo grafico) la stessa cosa succede per il circuito idraulico.
Le considerazioni fatte fin ora sono vere, però, solo in regime laminare perché solo qui troviamo un valore di x che cala in maniera inversamente reciproca alla velocità, troviamo una perdita lineare a quella velocità e quindi un valore di D P proporzionale alla perdita.
Questo è vero in regime laminare in quanto sappiamo che x = 64 / Re ma in regime fortemente turbolento, dove x non dipende più da Reynolds quindi non dipende più dalla velocità, x è una costante, questo porta ad avere una perdita proporzionale al quadrato della velocità e quindi sul diagramma prevalenza-portata avremo una parabola e non più una retta:
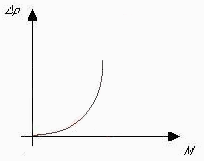
Figura 11:diagramma di un circuito idraulico in regime turbolento
Questa cosa ci fa capire che nel caso di regime turbolento il paragone con il circuito elettrico va a cadere perché abbiamo un carico alimentato dal nostro generatore che non ha una resistenza ohmica costante ma quadratica e quadratica risulta anche la perdita localizzata, ricordiamo infatti che Rloc = b (w2 / 2), quando sono in regime turbolento le due relazioni (parabola e retta) possono essere combinate insieme, possiamo cioè mettere assieme il concetto di perdita distribuita e perdita concentrata; questa cosa può essere effettuata introducendo il concetto di lunghezza equivalente.
CONCETTO DI LUNGHEZZA EQUIVALENTE
La presenza nel circuito all’interno di un condotto di una certa accidentalità è equivalente ad un condotto privo di accidentalità ma di lunghezza maggiore.
Facciamo un semplice esempio per capire:
prendiamo un tubo di lunghezza L e diametro D (figura 12) dove al centro di questo tubo è presente una strozzatura, un diaframma che induce una forte perdita localizzata con un b = 5 (ricordiamo che più il tubo è piccolo più b sale), allora la perdita totale di un oggetto di questo tipo diventa:
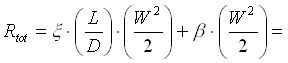
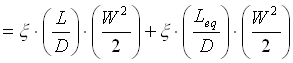
dove la lunghezza equivalente deve valere:
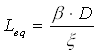
Che viene usata anche per calcolare la perdita totale data da:
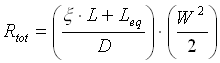
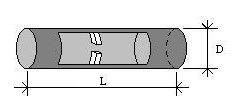
Figura 12
Vediamo ora come si determinano i valori della lunghezza equivalente.
Esistono anche qui dei tabulati grafici, si tratta di un anagramma cioè un’apparecchiatura grafica di calcolo (vedi figura 13) .
Cerchiamo di capire come si usa questo anagramma:
La lunghezza equivalente è un concetto che è rigoroso solo in regime perfettamente sviluppato quindi solo quando Reynolds non influenza più il valore di x , viceversa il coefficiente b è rigoroso in questo regime.
Finora abbiamo considerato solamente tubi tondi, andiamo ora a considerare tubi non tondi.
Noi sappiamo che quando un tubo è tondo il fattore di attrito è funzione del numero di Reynolds, (in regime laminare), tramite una costante che è 64, ma se il tubo non è tondo questa costante cambia.
Ad esempio per il tubo triangolare questa costante vale 53, per la corona circolare vale 96, mentre per il tubo rettangolare dipende dal rapporto tra i due lati, quando questo rapporto è piccolo ho un valore elevato (dato da 85) viceversa se questo rapporto cresce, il valore della costante è più basso (es. 57 se h / b = 1.0 ).
Questi valori sono tabellati (vedere figura 14).
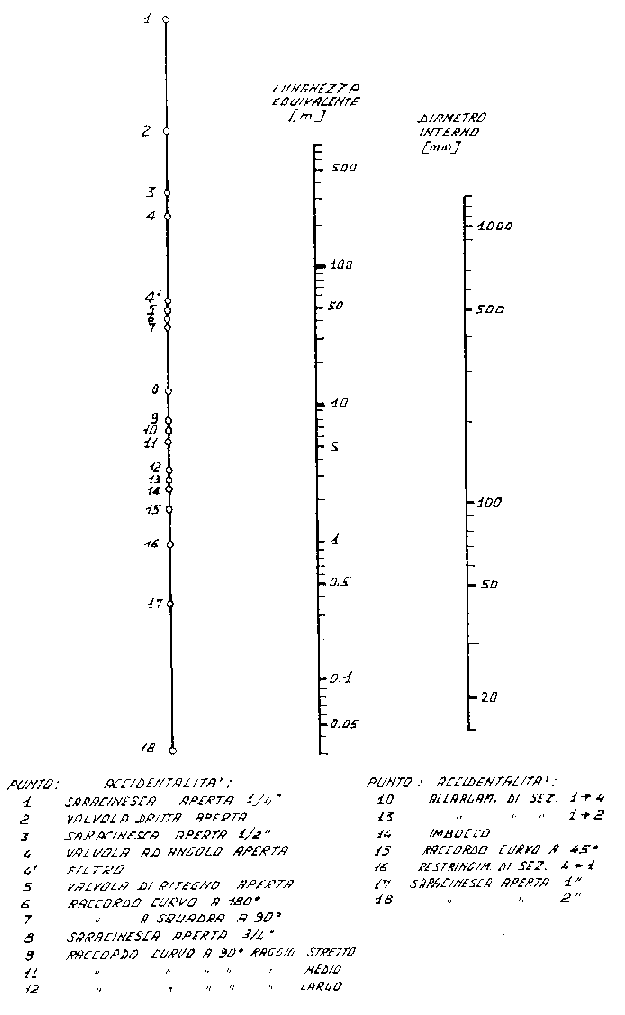
Figura 13
CONCETTO DI DIAMETRO EQUIVALENTE
Come si può vedere dalla tabella di figura 14 sotto riportata, nella colonna di sinistra sono riportati quei valori che ci consentono di affrontare il problema del calcolo della perdita distribuita in regime laminare mentre la colonna di destra ci consente di trovare il diametro equivalente di un condotto non tondo:
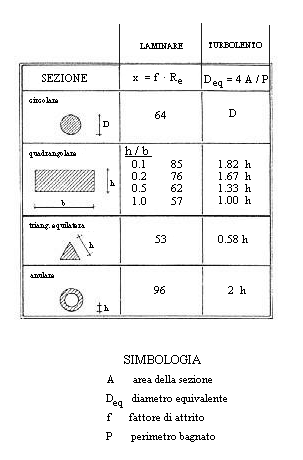
Figura 14
Inoltre mi rappresenta un valore che mi rende vero il diagramma di Moody per un tubo non tondo.
Il diametro equivalente è definito così:
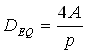
dove A rappresenta l’area e p il perimetro.
Facciamo un esempio:
prendiamo un quadrato di lato L (figura 15), allora il perimetro è dato da:
![]()
e l’area è data da:
![]()
Allora il diametro equivalente risulta essere:
![]()
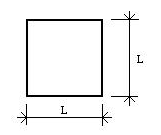
Figura 15
Un caso un po’ più particolare è quello della corona circolare (figura 16) dove Deq è dato da due volte la differenza tra i raggi (esterno ed interno):
![]()
Indicheremo la differenza tra i raggi h:
![]()
(Re = raggio esterno, Ri = raggio interno).
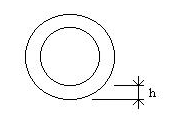
Figura 16
STRUMENTI PER LE MISURE FLUIDODINAMICHE
Andiamo ora ad analizzare quegli apparecchi che ci consentono di misurare o la velocità o la portata o entrambe le cose di un fluido che si muove in un condotto:
Metodo della pesata
E’ un metodo di misura della portata.
E’ presente un tubo dal quale fuoriesce un getto d’acqua che va a finire nel bacino sottostante, vediamo come viene effettuata la misura di portata di un fluido:
Facendo questo procedimento trovo il peso dell’acqua.
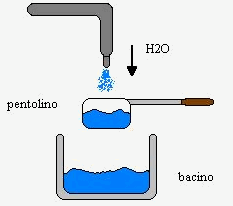
Figura 17
Definiamo ora la portata in massa come il rapporto tra il peso dell’acqua e il tempo t in secondi:
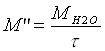
dove M è la massa dell’acqua.
La misura del tempo può essere fatta con un cronometro al centesimo di secondo e la portata dell’acqua su una massa d’acqua di alcuni litri può essere fatta sull’ordine del milligrammo.
I vantaggi di questo metodo sono:
L’unico suo difetto è che funziona solo con fluidi che nell’acqua non evaporano.
Tubo di Pitot
E’ un metodo di misura della velocità locale, viene utilizzato molto per la misura di velocità elevate, per esempio in galleria del vento, a bordo di aeroplani e dai paracadutisti.
E’ poco adatto però alle basse velocità, per esempio per i canali di ventilazione.
Questo metodo prende il nome di tubo di Pitot:
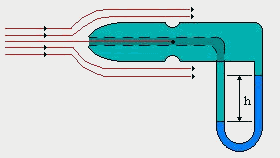
Figura 18: tubo di Pitot
Esiste anche una variante di questo tubo che prende il nome di Pitot-Prandal.
Vediamo ora come è fatto il tubo di Pitot:
è un tubo di acciaio inox a forma di L, lungo mezzo metro e di un centimetro di diametro.
Il fluido deve arrivare sulla punta del tubo che è arrotondata e il tubo deve essere orientato correttamente in modo da risultare parallelo ai fluidi che lo lambiscono.
Sulla sua punta il fluido si ferma e la velocità locale è v = 0, in questo punto esso ha esercita una sovrapressione (dovuta alla spinta del fluido che si sta arrestando), questa sovrapressione si chiama pressione di ristagno e il punto prende nome di punto di ristagno.
In questo punto il fluido ha una pressione maggiore della normale pressione Ps (pressione presente nel fluido prima del contatto di questo col tubo).
Se il tubo è ben raccordato allora dopo poco tempo sui suoi fianchi si ristabilisce la pressione Ps.
Come si può vedere dalla figura sotto (figura 19) nel tubo è presente un buco sulla punta e sono presenti altri due buchi sui lati dopo una distanza di cinque - otto diametri:
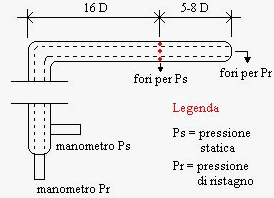
Figura 19
Nella cavità centrale è presente una pressione Pr detta di ristagno, mentre nelle altre due cavità è presente la pressione Ps.
Il fluido esterno non va a inserirsi all’interno dei fori, questi, però, consentono di mettere in comunicazione il liquido interno al tubo con quello esterno.
E’ possibile infine misurare le due pressioni Ps e Pr utilizzando due manometri.
Dalla differenza tra queste due misure ricaviamo la velocità v con cui il fluido urta la punta del tubo.
Manometro differenziale
Questo manometro non misura separatamente le pressioni Pr e Ps, ma direttamente la differenza di pressione.
Per fare questo si utilizza un dispositivo fatto cosi:
ho un liquido che in equilibrio è livellato, quando agendo sulle valvole metto in comunicazione le due camere, i due peli liberi si slivellano e questa variazione di liquido mi da la variazione della pressione presente tra le due camere.
La stessa tecnologia può essere interpretata in modo diverso nel cosiddetto:
Micromanometro a tubo inclinato
E’ sistema con due tubi collegati.
Quando il fluido è in equilibrio di pressione il pelo libero non si muove mentre quando si crea una differenza di pressione il livello del liquido tende a salire, quando questo si arresta, si va a leggere sulla scala graduata, presente sul tubo inclinato, il valore della differenza di potenziale.
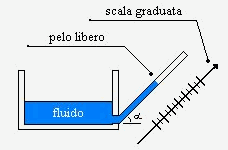
Figura 20
Questo manometro è molto sensibile ed è in grado di misurare delle differenze di pressioni dell’ordine dei milli Pascal.
Torniamo ora al nostro tubo di Pitot.
Normalmente il tubo viene inserito in un condotto di ventilazione tramite un foro, chiamato foro di ispezione, all’interno di questo condotto possiamo muovere il tubo di Pitot (per esempio lungo il diametro del condotto) e fare più misurazioni di velocità.
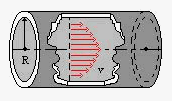
Figura 21
Ora consideriamo la figura sotto: chiamiamo A1,A2,A3 le aree delle tre semicorone e v1,v2,v3 le rispettive velocità misurate rispettivamente all’interno delle semicorone:
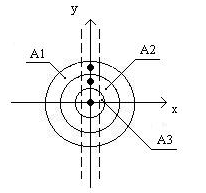
Figura 22
Allora la velocità media che indicheremo con W sarà data da:
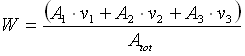
Come si può vedere dalla figura 21 le varie velocità vanno a descrivere una curva che non è altro che la parabola di Poiseville.
In regime turbolento però questo non è più vero perché i profili di velocità sono appiattiti, cioè graficamente avrei:
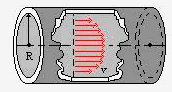
Figura 23
Mentre in regime laminare la vmax = 2 W, nel regime turbolento vmax può essere dell’ordine di 1,1 volte la W (cioè vmax = 1,1W)
Concludendo possiamo dire che questo strumento di misura si usa per velocità "robuste".
Ventoline
Sono ventole di alluminio protette da un pezzo di tubo metallico montate su una stecca con all’estremità un manico.
Sono presenti: un magnete ed un sensore; quando il magnete passa davanti al sensore questo capta degli impulsi elettrici che vengono amplificati e arrivano ad una centralina che mi riporta il numero di giri che sta facendo la ventolina.
Dal numero di giri posso ricavare il valore della velocità del fluido che sta facendo girare la ventolina.
Solitamente le ventoline vengono utilizzate negli impianti di ventilazione.
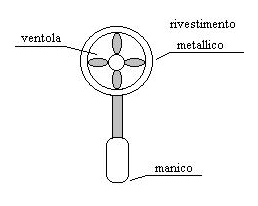
Figura 24: ventoline
Tubo di Venturi
è è
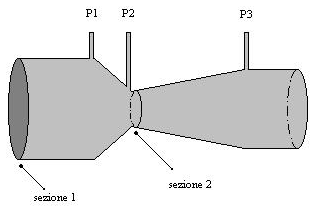
Figura 25: tubo di Venturi
Come si può vedere dalla figura questo tubo è caratterizzato da un brusco divergente ed un dolce convergente è può lavorare solamente nel verso indicato dalle frecce in figura.
Si tratta di un tubo che può essere installato in maniera permanente o semi-permanente all’interno di un impianto:
nel primo caso il tubo è parte integrante dell’impianto cioè è fisso e può essere isolato semplicemente andando a chiudere delle apposite valvole;
nel secondo caso invece l’impianto è dotato di un tubo estraibile, questo tubo viene scambiato col tubo di Venturi nel momento in cui questo viene a servire:
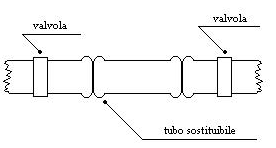
Figura 26
Il tubo di Venturi viene utilizzato per il calcolo della portata di un fluido.
Vediamo come si effettua la misura della portata:
io so che nella sezione 1 la pressione P1 è maggiore della pressione P2 presente nella sezione 2, questo succede perché se andiamo a scrivere l’equazione del bilancio dell’energia tra le 2 sezioni otteniamo:
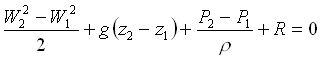
Le perdite le trascuro perché sono in un convergente, cioè il tubo tende a stringersi, e noi sappiamo che in un convergente non ci sono perdite (viceversa in un divergente le perdite esistono) e poiché so che nella sezione 2 la velocità sarà maggiore di quella presente nella sezione 1, da questa relazione discende che la pressione è nulla.
Vediamo ora come si può ricavare la velocità dalla relazione sopra:
osserviamo che ho due incognite e una sola relazione, allora utilizzo l’equazione di continuità:
![]()
ma se ipotizzo che r costante (il che vuol dire che il mio sistema funziona bene con l’acqua e funziona meno bene con l’aria), allora:
![]()
![]()
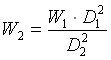
Sostituendo ora W2 trovato nell’equazione di continuità trovo:
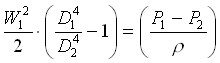
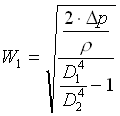
che rappresenta la velocità media nella sezione 1, noto il salto di pressione tra le due sezioni, (D p), che viene misurato utilizzando il manometro differenziale sopra descritto.
Confrontiamo ora l’espressione finale con quella del tubo di Pitot dove avevo:
v1 = 0 P1 = Pr (pressione di ristagno)
v2 = ¥ P2 = Ps (pressione statica)
allora scrivendo anche qui l’equazione del bilancio dell’energia e trascurando la perdita di carico trovo:
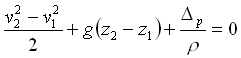
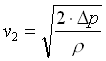
si nota quindi che le due relazioni sono molto simili tra loro.
Diaframma o Boccaglio
Anche in questo caso come per il tubo di venturi si va a misurare tramite un manometro, la variazione di pressione D p presente tra due punti.
Sono quindi entrambi misuratori di portata che si basano sull’introduzione volontaria in un condotto di una perdita di carico concentrata
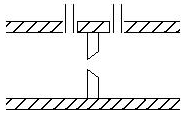
Figura 27: diaframma
In questo caso quindi nell’equazione del bilancio dell’energia non posso più trascurare la perdita, ma è anche vero che avendo il tubo un diametro costante, la velocità sarà la stessa (perché è costante la portata), allora nell’equazione del bilancio dell’energia avrò:
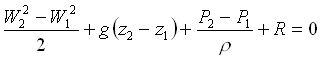
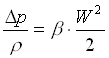
da cui ricaviamo la velocità W
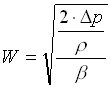
dove b è il coefficiente di perdita localizzata.
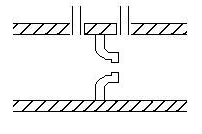
Figura 28: boccaglio
Rotametro
Tratto di condotto verticale trasparente all’interno del quale è presente un galleggiante. Il condotto, come si può vedere dalla figura 28, tende a divergere questo fa si che il fluido che scorre all’interno del tubo (solitamente acqua) tende a trascinare il galleggiante verso l’alto.
Arrivato ad una certa quota il galleggiante si stabilizza perché la velocità cala in maniera tale che la forza peso, che tende a tirarlo verso il basso, e la forza di trascinamento, che tende a tirarlo verso l’alto, sono in equilibrio.
Il vetro è graduato, quindi andando a leggere sulla scala il valore che corrisponde alla posizione raggiunta dalla sommità del galleggiante troviamo la portata del fluido che sta scorrendo in quel momento all’interno del tubo.
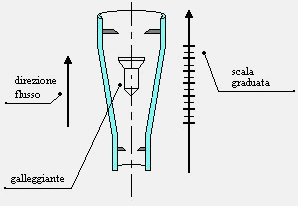
Figura 29: rotametro
Il difetto di questo metodo è che è impreciso e deve essere tarato con il metodo della pesata visto in precedenza.
Supponiamo che il fluido che scorre al suo interno sia acqua, io so che la viscosità dell’acqua varia con la temperatura, e quindi il rotametro è costretto a funzionare a temperatura diverse e quindi a scalibrarsi.
Si capisce allora che un altro difetto è dato dal fatto che la forza di trascinamento dipende dalla viscosità del fluido, quindi questo strumento va tarato per un fluido specifico, cioè se cambia il fluido che scorre al suo interno allora deve essere tarato nuovamente.
Anemometro laser-Doppler
Questo strumento si basa sul fenomeno ottico dell’interferenza.
Noi sappiamo che quando abbiamo due raggi di luce tra loro coerenti e si incrociano, si crea nella zona di incrocio il fenomeno delle frange di interferenza.
Le frange in questa zona sono visibili e vanno dalle poche decine alle centinaia.
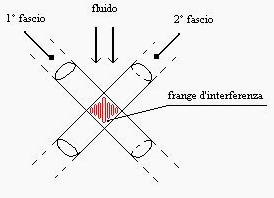
Figura 30
Ora se inserisco un fotomoltiplicatore ottengo un segnale elettrico, che è una tensione proporzionale all’intensità luminosa.
Se noi questo segnale lo andiamo a vedere con un oscilloscopio troviamo una serie di picchi che mi rappresentano le particelle che stanno attraversando il volume di misura.
Se queste particelle hanno velocità v allora questi picchi avranno una frequenza f data da:
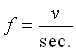
questa frequenza è quindi proporzionale alla velocità del fluido.
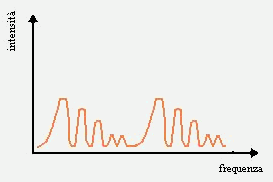
Figura 31
Il difetto principale è di tipo ottico in quanto non è semplice mandare il fascio luminoso all’interno dei tubi.
In oltre il fluido non deve essere pulito.
Se fosse pulito avrei dei problemi a determinare il verso delle particelle, per distinguere il verso si fa in modo che i due raggi laser non siano perfettamente identici, si introduce una variazione di frequenza tra i due raggi di 40 MHz, facendo così le frange non sono ferme ma sono in movimento.
Se il fluido è fermo la f0 = 40 MHz, se invece il fluido si muove incontro alle frange, l’effetto Doppler fa si che la frequenza cresca fino ad un valore pari a f0 = 40,3 MHz dove la frequenza Doppler vale:
f D= 0,3 MHz
Se infine il fluido si muove nella stessa direzione delle frange di interferenza misurerò una frequenza f0 = 39,7 MHz dove la frequenza Doppler vale:
f D = - 0,3 MHz
Altri metodi
Esistono infine dei sistemi elettrici ed elettromagnetici che mi consentono di calcolare la quantità di fluido che passa all’interno di un condotto, ma questi sistemi solitamente sono imprecisi.
APPLICAZIONI
Esempi di applicazione dell’equazione del moto per correnti fluide in moto unidimensionale stazionario.
Se la pompa viene inserita in un circuito chiuso schematizzato in figura 32 e si suppone il fluido incomprimibile, l’equazione data da
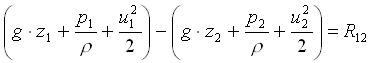
(che è l’equazione per un fluido incomprimibile), applicata tra le sezioni 1 e 2 diventa:
![]() (R12 = perdita di carico)
(R12 = perdita di carico)
avendo trascurato le differenze di quota tra le sezioni a valle e a monte della pompa e ammettendo che la velocità nelle due sezioni sia uguale,
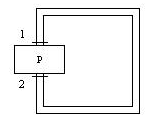
Figura 32
se, come spesso avviene, i condotti a monte e a valle della pompa hanno le stesse sezioni. In questo caso la pompa deve sopperire alle sole perdite di carico che il fluido incontra nel suo moto entro i condotti. Queste perdite dipendono, per un certo fluido, dalla portata in volume Q e dalle caratteristiche geometriche del condotto, secondo la relazione data da:
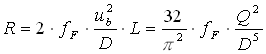
dove D e L sono rispettivamente la lunghezza e il diametro del condotto.
Il valore delle perdite di carico, almeno di quelle ripartite, viene così a dipendere dalla quinta potenza del diametro stesso e di conseguenza la prevalenza della pompa è tanto maggiore quanto più piccola è la sezione dei tubi che si adottano nei circuiti.
Viceversa maggiore è la sezione dei condotti e minore la perdita di carico e perciò la prevalenza, e di conseguenza la potenza installata, della pompa.
La scelta del diametro del condotto ha pertanto un’influenza decisiva sul valore delle caratteristiche della pompa che viene inserita nel circuito e di conseguenza il costo d’impianto e di esercizio dipende in maniera essenziale da questa scelta.
Facciamo una breve parentesi:
l’equazione data da:
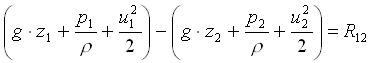
nel caso più generale per un fluido compressibile assume la forma seguente:
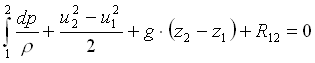
e sotto tale forma andrebbe applicata nel caso particolare del moto di aria in un qualunque circuito aperto o chiuso .
Si abbia, infatti, un circuito di canali qualsiasi, in cui si muova una certa portata d’aria ed in cui sia inserito un ventilatore, quale può aversi per esempio nel caso di un impianto di condizionamento d’aria.
In tal caso, considerata l’aria come un gas ideale si potrebbero scrivere le equazioni di stato dei gas ideali p v = RT, dU = g v dT e l’equazione della trasformazione particolare che avviene durante il moto, ad esempio una politropica:
![]()
Si potrebbe cosi risolvere l’integrale:
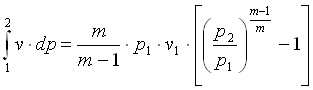
Tuttavia facciamo l’ipotesi che la pressione tra le sezioni 1 e 2 varia solo di qualche percento, allora sotto questa ipotesi è lecito ammettere che il volume specifico rimanga costante e scrivere quindi l’equazione vista sopra per il fluido incomprimibile, ciò che equivale a fermarsi al primo termine dello sviluppo in serie
del termine 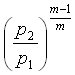 .
.
Dato il circuito schematicamente rappresentato in figura 33 con un condotto di aspirazione dall’esterno, un ventilatore, ed un condotto di mandata si potrà scrivere, tra le sezioni S1 e S2 :
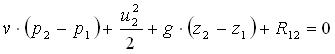
avendo scelto la sezione S1 abbastanza lontana dall’imbocco del condotto in modo tale da trascurarne la velocità u1.
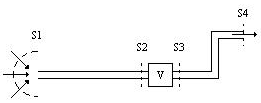
Figura 33
Tra le sezioni S2 e S3, chiamata W23 l’energia che il ventilatore fornisce all’unità di massa di fluido:
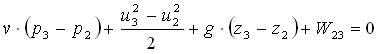
Tra le sezioni S3 e S4:
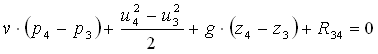
Sommando si ottiene, poiché le pressioni nelle sezioni S1 e S4 sono uguali e pari a quella atmosferica pa e la differenza di quota è generalmente trascurabile:
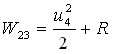
dove si è posto R= R12 + R34.
L’andamento delle pressioni lungo l’asse del canale è dato da:
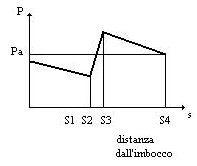
Figura 34
Occorre tuttavia ricordare che p3 - p2 rappresenta solamente qualche percento di pa, mentre in figura tale differenza appare molto maggiore per comodità di rappresentazione.
Per quanto riguarda R va notato che, nel caso di un liquido le perdite di carico ripartite sono in generale molto maggiori di quelle concentrate (per cambiamenti di sezione o di direzione nel condotto, ecc.), tanto che spesso di queste ultime si può tener conto, aumentando di una certa percentuale, che rimane in generale sempre in limiti abbastanza ristretti, quelle ripartite, nel caso di condotte d’aria le perdite ripartite e concentrate sono dello stesso ordine di grandezza , anzi quelle concentrate sono, in generale, preponderanti.
E’ necessario però nel valutare il termine R tenere separate le perdite ripartite da quelle concentrate, le quali d’altronde dipendono grandemente dalle caratteristiche geometriche e costruttive degli elementi particolari che le producono.
APPENDICE
|
materiale |
e (mm) |
|
acciaio chiodato |
0.0 – 9.0 |
|
cemento |
0.3 – 3.0 |
|
doghe in legno |
0.19 – 0.9 |
|
fusione in ferro |
0.25 |
|
ferro zincato |
0.15 |
|
ferro asfaltato |
0.12 |
|
acciaio commerciale |
0.046 |
Al diagramma di Moody viene generalmente allegata una tabella che riporta i valori della scabrezza per i materiali con cui tipicamente si realizzano i tubi per il trasporto dell’acqua.
Questi valori si trovano anche in opportuni diagrammi vedi fig. 35
|
Resistenze |
Leq / D |
|
Gomito a 45° |
15 |
|
Gomito a 90° |
75 |
|
T attraversamento diretto |
20 |
|
T uscita laterale |
60 |
|
T entrata laterale |
70 |
|
Valvole per ¾ chiuse |
800 |
|
Valvole per ½ chiuse |
200 |
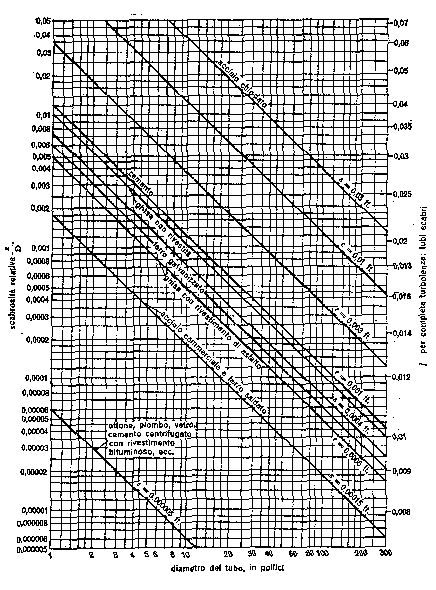
Figura 35