Onde sferiche

Le equazioni unidimensionali, ricavate nelle precedenti lezioni in un sistema di coordinate cartesiane, valgono per la propagazione di onde piane lungo una sola dimensione.

In una stanza senza eco o nello spazio libero, si preferisce esprimere matematicamente la propagazione del suono come proveniente da una fonte sferica o non direzionale. In questo caso, l’onda sonora si espande per effetto di contrazioni ed espansioni come se si allontanasse dalla sorgente creando un fronte d’onda costituito da superfici sferiche concentriche.

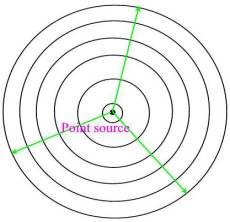
Figura 1: Propagazione dell’onda sferica

Per applicare le equazioni d’onda alle onde sferiche, dobbiamo modificare alcuni operatori e passare a coordinate sferiche polari.

Supponendo per ipotesi una eguale propagazione in tutte le direzioni, l’equazione d’onda unidimensionale nel nuovo sistema di coordinate risulta essere:

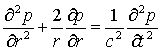(1)

dove:

· p(r,t) è la pressione dell’onda

· r è il raggio distanza dal centro delle sfere concentriche

· c è la velocità del suono

· t è il tempo

Una semplice sostituzione ottenuta ponendo mi permette di riscrivere la (1) come:

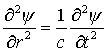(2)

E’ doveroso notare che p era funzione di x e di t mentre la nuova variabile è funzione di r e di t.

Una soluzione a questa nuova equazione differenziale – ricordandomi della sostituzione effettuata – può essere espressa come:

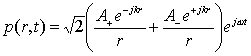(3)

Dove è la grandezza della pressione sonora dell’onda uscente ad una distanza unitaria dal centro della sfera; conseguentemente è la stessa cosa per l’onda riflettente. Se non vi è nessuna superficie riflettente nel mezzo, è necessario solo il primo termine dell’equazione.

Nell’esempio del pistone era ovvio considerare l’esistenza di un’onda destra e di una sinistra rispetto allo stantuffo, ma nel caso di onde sferiche non studiamo mai l’onda implodente data l’evidente situazione di asimmetria e la sua non utilità. In realtà l’onda implodente risulta assai utile nello studio e nella progettazione della bomba atomica. Essa infatti scoppia grazie ad un’onda implodente che esercita una pressione dall’esterno. Si avvicina il materiale fissile,cioè i nuclei degli atomi , si vincono così le forze intermolecolari e si inizia il processo di fusione a catena.

Vediamo ora di assegnare anche una velocità alle particelle in moto. Sapendo che:

(4a)

dove q è il vettore velocità della particella, riesco a scrivere che:

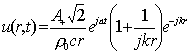(4b)

E’ immediato, arrivati a questo punto, andare a ricavare l’impedenza acustica specifica data dal semplice rapporto tra l’equazione (3) e la (4b):

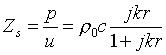(5)

Al tendere di kr all’infinito posso riscrivere la (5) come:

(5b)

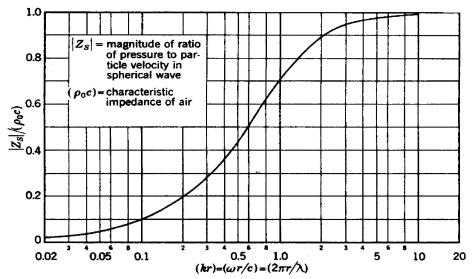
Figura 2: Andamento del modulo dell’impedenza in funzione di kr

L’impedenza in questo caso è quasi puramente resistiva e circa uguale alla impedenza caratteristica di un’onda piana. In altre parole, l’impedenza acustica specifica a larga distanza dalla sorgente sferica è circa uguale a quella calcolabile in un tubo nel quale non vi siano riflessioni dalla parete posta a chiusura del tubo stesso.

Le equazioni (3) e (4b) mi confermano allora quanto detto e - sarà oggetto di alcune riflessioni più avanti - mi rivelano le differenze tra la risposta di un microfono sensibile alla pressione ed uno invece sensibile alla velocità delle particelle d’aria quando essi si trovano vicini ad una piccola sorgente di suono a basse frequenze.

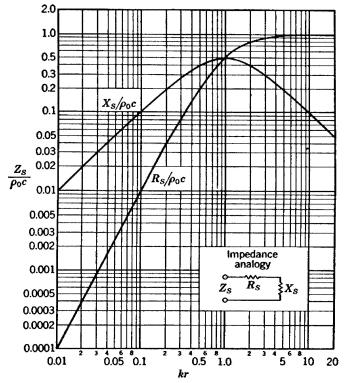
Figura 3: Andamento della parte reale ed immaginaria di Z in funzione di kr

Noto quindi che l’impedenza non è più una quantità sempre reale ed ha una fase non costante poiché la parte reale ed immaginaria variano con r. Facciamo qualche altro piccolo ragionamento: per kr che tende all’infinito, la parte reale dell’impedenza tende al valore r_oc mentre quella immaginaria diventa piccola. Per kr invece che tende a zero la parte reale decresce e predomina quella immaginaria

E’ immediato allora notare che pressione e velocità sono fuori fase di 90°: questo mi porta a dire che l’energia è nulla. Avendo infatti imposto un certo valore di potenza nella sorgente, questo si traduce in oscillazioni di pressione e di velocità davvero enormi rispetto al prodotto dei loro moduli. Su una superficie sferica molto piccola il prodotto tra P ed U è molto più grande di intensità equivalentemente trasmessa. Cerchiamo di chiarire il discorso: questo vuol dire che non posso avere una sorgente puntiforme; al limite, per il tendere a zero delle dimensioni della sferetta, la potenza va a zero. Se non voglio che la mia efficienza scenda troppo, comunque devo avere una sorgente relativamente grande. Questo è particolarmente importante per le basse frequenze. Sull’ascissa del grafico va sottolineato la presenza di kr con k=/c; andare a sinistra sul diagramma vuol dire andare al centro della sfera e giù di frequenza: ecco perché a basse frequenze ci vuole una sorgente grossa. Gli altoparlanti per le basse frequenze, ne sono un esempio.

Se per caso realizzassi un altoparlante piccolo, che magari meccanicamente riuscisse a dare tutta la potenza che voglio al piccolo pistone che va avanti e indietro, questa potenza non verrebbe lanciata nell’aria perché il campo acustico reagirebbe male ed in maniera inaspettata. E’ una questione puramente geometrica: non dipende dall’ambiente o dal materiale con cui è stato fabbricato; non ho potenza acustica perché la legge trovata mi porta a sfasare la pressione facendomi rilevare energia nulla.

Una parziale soluzione al problema ci giunge dagli altoparlanti a tromba. Una tromba è in effetti un trasformatore acustico. Esso è in grado di incrementare la potenza di uscita senza il problema della risonanza che generalmente si riscontra nei coni. Un diaframma che ha un’area larga, ha un impedenza di radiazione che è molto più resistiva oltre la frequenza desiderata, rispetto ad uno che ha un’area piccola. Come principale conseguenza ho una maggiore potenza irradiata a basse frequenze per un dato volume di velocità d’aria. Essi sono largamente usati nei cinema, teatri e nei concerti: ovunque deve essere irradiata una grossa potenza acustica e dove è desiderato il controllo della direzione sonora. Quest’ultima caratteristica però è anche uno dei suoi limiti: l’alto costo, le dimensioni maggiori ed una non omogenea propagazione frenano il più delle volte il suo utilizzo.

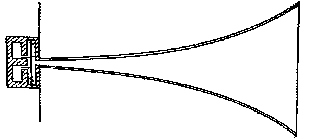
Figura 4: Altoparlante a tromba

Definisco ora l’intensità di un’onda sferica come il tempo medio durante il quale l’energia fluisce attraverso una regione di area unitaria nel mezzo acustico. Nel sistema mks le unità dell’intensità sono watt per metro quadro. L’intensità è il prodotto della pressione sonora per la componente in fase della velocità della particella. Possiamo calcolare l’intensità media in un certo punto del mezzo lungo una data direzione tramite l’equazione:

(6a)

dove:

· p* è il complesso coniugato della pressione sonora

· q è velocità complessa della particella nella direzione in cui l’onda viaggia

· è l’angolo tra la direzione di spostamento e la direzione in cui l’intensità viene determinata

Calcoliamo ora l’intensità nel caso di un’onda sferica. Poniamo per definizione:

(6b)

Allora:

(6c)

e la velocità complessa della particella è pari a:

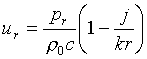(6d)

e sostituendo semplicemente i valori, ottengo:

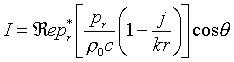(7)

Un’espressione più interessante è possibile ricavarla da questa ultime equazione: la potenza totale per ogni raggio r è uguale a:

(7b)

Quindi per un’onda sferica ottengo un importante risultato:

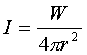per (8)

Per la legge della conservazione dell’energia, W è indipendente da r se non ci sono perdite nel mezzo così che l’intensità varia inversamente col quadrato della distanza r. Dall’equazione 6b invece si nota che p_rvaria con l’inverso della distanza.

Applicazione ai microfoni

Rovesciamo ora il discorso e vediamo cosa succede nel caso io abbia un microfono. I microfoni sono trasduttori elettroacustici, il cui scopo è quello di trasformare il segnale sonoro, caratterizzato da una variazione di pressione, in segnale elettrico. In base a come avviene questa trasformazione, i microfoni si possono dividere in due grandi classi: microfoni dinamici e microfoni a condensatore.

Nei microfoni dinamici le onde provocano la vibrazione di un sottile diaframma metallico il quale provoca a sua volta la vibrazione di una bobina ad esso collegata e immersa in un campo magnetico generato da un magnete fisso. Tale movimento della bobina crea delle correnti elettriche che riproducono il comportamento delle onde sonore di partenza. Questo tipo di microfono è particolarmente adatto per riprendere strumenti singoli e non richiede alimentazione.

Nei microfoni a condensatore il diaframma costituisce una delle due armature di un condensatore tra cui viene prodotto un potenziale elettrico applicando un basso voltaggio per mezzo di una sorgente (batteria), che può essere interna o esterna al microfono stesso. Il potenziale elettrico prodotto dipende dal voltaggio della sorgente, dall'area dell'armatura e dalla loro distanza. Il diaframma è mobile e cambia posizione in risposta al suono incidente. La corrente prodotta è però tanto debole da dover essere amplificata in uno stadio immediatamente successivo. Una variante di questa configurazione utilizza un diaframma di materiale plastico con una carica permanente.

Le caratteristiche principali di un microfono sono la sensibilità, definita come il rapporto tra la tensione d’uscita e la pressione acustica del campo sonoro, la risposta in frequenza, cioè il modo di variare della sensibilità in funzione della frequenza dell’onda sonora e infine la direzionalità, cioè il modo di variare della sensibilità con la direzione d’arrivo del suono. In pratica si riscontra che la sensibilità decresce al diminuire del diametro del microfono stesso, mentre la gamma utile in frequenza aumenta. E’ chiaro quindi che l’uso di un microfono che abbia una banda passante molto ampia, paga il prezzo in termini di sensibilità e viceversa.

Riuscire a scegliere un microfono adatto per tutti i tipi di misura è praticamente impossibile: avere una buona sensibilità va a scapito di una buona risposta in frequenza e viceversa. Esistono comunque dei microfoni di utilità generale che riescono ad avere dei compromessi fra i vari fattori.

I microfoni a condensatore sono di qualità sicuramente superiore rispetto ai microfoni dinamici: hanno una maggiore sensibilità, una risposta in frequenza più lineare ed estesa e un rumore di fondo bassissimo. Queste qualità ne limitano anche l'impiego: sono adatti a riprendere solo quegli strumenti che non hanno transitori troppo potenti (sono l'ideale per le voci).

Microfono a velocità pura

E’ un particolare trasduttore che risponde alla differente pressione tra due punti molto vicini tra loro. Il modello più elementare prevede un diaframma con entrambi i lati esposti all’onda sonora.

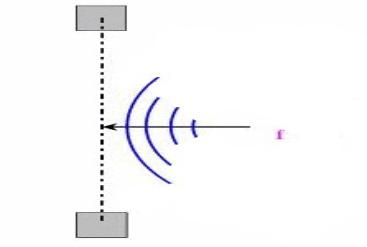
Figura 5: Schema di un microfono a velocità

Se un microfono a velocità molto piccolo è posto in una certa direzione x, la forza che lo muove è data da :

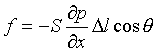(9)

dove:

· p è la pressione sonora

· è la componente del gradiente di x della pressione che agisce attraverso le facce del diaframma

· è l’angolo che la normale al diaframma fa con la direzione di moto dell’onda.

· è l’effettiva distanza tra i due lati del diaframma

· S è l’area del diaframma

Questa relazione è vera per qualsiasi tipo di onda. Inoltre per ogni data frequenza , la risposta del microfono è proporzionale a cos creando la caratteristica relazione ad 8.

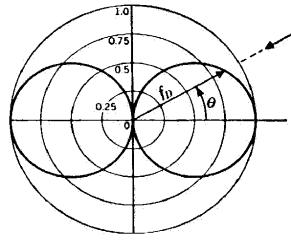
Figura 6: Direttività di un microfono a velocità

Il grosso vantaggio di questo microfono è la sua direzionalità. Allo stesso tempo questa direzionalità è bilatera ossia il microfono cattura i suoni provenienti anche dal lato opposto a quello in cui è direzionato. Questo mi porta ad avere onde costruttive o distruttive che si vanno a sovrapporre a quella che realmente mi interessa distorcendomela o addirittura annullandola. Un altro sgradevole svantaggio è l’effetto di prossimità. Si nota da questa curva che l’uscita del microfono aumenta col diminuire della frequenza, quindi, quando una persona parlando o cantando si muove vicino a questo tipo di microfoni la sua voce diventa grave o acuta. E’ per questa ragione che la voce di radio cronista suona cupa quando parla molto vicino ad un microfono sensibile alla velocità che è stato invece progettato per dare il massimo quando posizionato ad una maggiore distanza dalla sorgente. I cantanti professionisti sfruttano questa variazione di risposta timbrica per equalizzare la voce.

Figura 7: Uso del microfono in studio di registrazione

Microfoni Misti

Questo tipo di microfono risponde sia alla velocità che alla pressione di un’onda. Questo mi permette di produrre uno schema che ha un solo massimo (caratteristica unidirezionale). Le due unità devono essere posizionate il più vicino possibile così che la risultante caratteristica sia indipendente alla frequenza. I microfoni con questa caratteristica sono usati prevalentemente nelle trasmissioni dove si vuole sopprimere i suoni indesiderati che provengono – rispetto al microfono – dalla parte opposta.

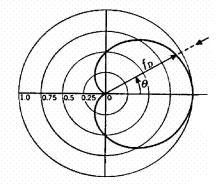
Figura 8: Figura di direttività a cardioide

Se la proporzionalità tra la pressione e la velocità è del 50% allora la figura di direttività è una cardioide; in caso contrario ho un ipercardioide - aumentando la velocità - o una subcardioide aumentando la componente in pressione.

In commercio si possono trovare diversi tipi di microfoni con queste caratteristiche: alcuni già tarati, altri che mi permettono di scegliere la proporzione tra la pressione e la velocità desiderati, permettendo di scegliere in loco la modalità preferita e altri ancora che mi danno uscite specifiche per pressione e velocità permettendomi di comporre il segnale desiderato in post produzione. E’ vero che i canali in questo caso raddoppiano, avendo ben quattro canali supponendo le uscite stereo, ma li posso sempre mixare.

Microfoni Virtuali

Supponiamo ora di avere tre microfoni a velocità posizionati lungo le componenti cartesiane ed uno a pressione posizionato al centro, ottenendo lo schema in figura 9. Ho così quello che si chiama un B-Format. Il concetto di tridimensionalità può essere confermato con le proprie orecchie . Quando si ascolta un suono – come il canto di un uccellino su un albero – siamo in grado all’istante di dare una collocazione nello spazio alla sorgente del suono. Il B-Format non fa altro che definire il suono in tre dimensioni. La sua comodità inoltre sta nel poter registrare il suono e poi ridirezionarlo a mio piacere in un secondo momento. Si pensi all’esecuzione di una canzone con un orchestra di numerosi elementi. In post produzione posso regolare la direzione di prelevamento del suono in modo da esaltare l’assolo di uno strumento o – viceversa – nascondere la stonatura di un altro. Per questa realizzazione i microfoni soundfield (www.soundfield.com ) risultano i migliori .

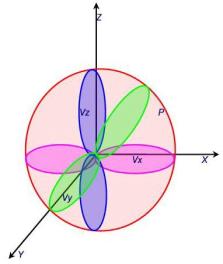
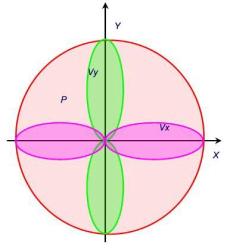
Figura 9: Figura di direttività in tre dimensioni ed in pianta

Microfoni da misura: i Fonometri

La misura della pressione sonora e della velocità delle particelle sono di necessaria utilità per chi lavora nel campo dell’acustica. Lo strumento utilizzato - chiamato fonometro - è sostanzialmente un microfono da misura a pressione.

Figura 10: Fonometro della Larson & Davis (L&D-824)

Da quanto detto prima per i trasduttori risulta che quando si usa il microfono accoppiato meccanicamente con l’amplificatore occorrerà fare attenzione affinché il corpo dello strumento non si comporti da riflettore per le frequenze le cui lunghezze d’onda coincidono con le dimensioni del fonometro. La migliore alternativa è sempre quella di allontanare il microfono dal fonometro per uno o più metri anche considerando il fatto che il corpo dell’operatore è a sua volta un riflettore. Dovendo operare da vicino è bene usare per il microfono una prolunga con il cavalletto. La parte del fonometro volta alla sorgente di rumore ha una forma affusolata tale da deviare le riflessioni rispetto al microfono. L’ingombro frontale è ridotto al minimo in modo da riflettere solo suoni con frequenze molto elevate.

Figura 11: Rilevazioni fonometriche in una strada trafficata

Vediamo lo schema di funzionamento a blocchi:

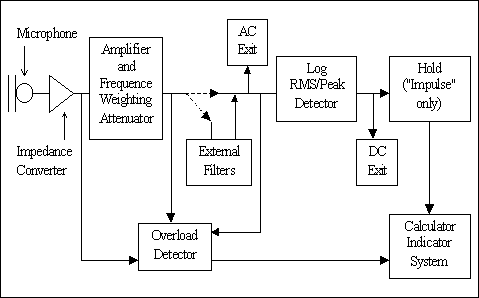
Il microfono è tradizionalmente a condensatore in quanto è l’unico traduttore elettroacustico che risponde unicamente alla pressione. Le sue caratteristiche gli garantiscono una notevole precisione e non vengono influenzate dall’umidità e dalla temperatura entro limiti molto ampi. E’ una capsula del diametro di circa 12 cm il cui diaframma è fatto di un film plastico metallizzato molto sottile; la membrana è rivestita di quarzo per garantire la massima protezione in ambienti umidi e corrosivi. In questo caso è necessario usare i tipi di microfoni provvisti di foro di compensazione della pressione statica e dotarli di deumidificatori, del dispositivo parapioggia e dell'indispensabile schermo controvento. L’armatura del microfono è fissa mentre sotto la griglia di protezione c’è il diaframma che fluttua avanti e indietro mosso dalla pressione dell’aria. Varia allora la capacità del condensatore costituito dal foglietto che vibra e l’armatura metallica che ci sta dietro: la variazione di capacità viene tradotta in una “tensione” proporzionale al movimento della membrana da un piccolo preamplificatore di tipo FET; porta poi fuori un segnale che è proporzionale come tensione alla pressione d’onda: il rapporto di conversione si chiama sensibilità del microfono ed ha un valore compreso tra i 10 e i 50 mV/Pa.

Dopo il preamplificatore è previsto un blocco che rivela la presenza di una situazione di sovraccarico presente in ingresso e tiene sotto controllo la dinamica del segnale in arrivo, inoltre avverte tramite una indicazione sul display la presenza di eventuali sovraccarichi. In tal caso l’operatore potrà aggiustare il fondo scala agendo con appositi commutatori su un attenuatore d’ingresso, il quale permette di regolare l’escursione del segnale amplificandolo o attenuandolo a secondo dei casi.

Successivamente il segnale incontra dei particolari circuiti di filtraggio che provvedono a pesare opportunamente il segnale. E’ relativamente semplice fabbricare un circuito elettronico dove la sensibilità vari con la frequenza, nello stesso modo come per l'orecchio umano, simulando le curve di uguale sensazione sonora. Sono state sviluppate tre curve caratteristiche e normalizzate internazionalmente definite come ponderazioni “A”, “B” e “C”.

Il circuito di ponderazione “A” rappresenta una buona approssimazione per le curve di uguale sensazione sonora ai bassi livelli di pressione sonora, il circuito "B" si comporta analogamente per le curve di uguale sensazione sonora a livelli medi di pressione sonora, mentre il circuito “C” si comporta analogamente agli elevati livelli di pressione sonora. Attualmente la ponderazione “A” è la più utilizzata, poiché “B” e “C” non si correlano a causa delle curve di uguale sensazione sonora che sono basate su delle prove con toni puri, mentre i suoni che incontriamo più frequentemente sono dei segnali complessi contenenti un infinito numero di toni differenti.

In questo modo viene modificata la sensibilità dello strumento alle varie frequenze e, per il caso della curva “A”, rendendola uguale con buona approssimazione a quella dell’orecchio umano. Solo per qualche fonometro è possibile inserire un pacco filtri esterno switch-out a baionetta che consentono di eseguire l’analisi in frequenza in banda d’ottava e terzi d’ottava, necessaria per l’individuazione delle varie componenti tonali del segnale. Dopo una opportuna amplificazione intermedia, il segnale entra in un blocco rettificatore che provvede ad estrarre il suo valore efficace (RMS). In questo blocco sono normalmente inserite le costanti di tempo che sono note come: FAST (veloce), SLOW (lento) ed in alcuni IMPULSE (impulso) e PEAK (picco). In pratica con esse si determina la risposta dello strumento alle variazioni del segnale. Nella maggior parte dei casi la misura del suono riguarda segnali fluttuanti, cioè segnali che variano continuamente il loro livello e per effettuare una misura corretta bisogna essere in grado di apprezzare nella maniera più accurata possibile le variazioni del segnale. Se però il livello di pressione fluttua troppo rapidamente, l’ago del display analogico può muoversi in maniera così irregolare da rendere impossibile la lettura di un valore significativo.

Per questa ragione sono stati standardizzati vari tempi di risposta dello strumento ponendoli a:

· FAST a 125 ms (1/8 di secondo)

· SLOW a 1 sec

· IMPULSE a 35 ms di salita e 1,5 sec in discesa

Nei moderni fonometri però , il problema della misura di rumori oscillanti viene parzialmente risolto utilizzando un display digitale ; in tal caso il valore delle misure viene aggiornato ogni secondo riportando il valore efficace (RMS) massimo che lo strumento ha misurato nel secondo precedente. Vi è poi parte di analisi del risultato, che può essere un circuito di memoria che consente di memorizzare l’ultimo valore massimo e poi c’è un processore digitale finale che costituisce sostanzialmente il display dello strumento.

Risulta inoltre molto utile la presenza di due uscite AC da cui è possibile prelevare il segnale elettrico. Ma cosa vuol dire questo ? Nella prima uscita mi trovo un segnale aumentato in ampiezza e ponderato magari dalla presenza di uno o più filtri; nella seconda invece è già parzialmente ponderato: la soluzione più comune è quella di campionarli – interagendo con la scheda audio – o registrarli direttamente su un determinato supporto. Questo risulta molto utile quando non si ha tempo di fare tutte le valutazioni del caso. C’è comunque da dire che gli strumenti moderni tendono a fare comunque le analisi e le mettono nei dischi fissi interni in modo da garantire una copi di riserva. La normativa italiana permette di registrare e di analizzare in un secondo tempo a patto che gli strumenti siano di tipo “loss-less”. Ma vediamoli più in dettaglio:

· Professionali: sono registratori digitali che usano un supporto magnetico; le due case leader nel settore sono la Tascam (www.tascam.com) che utilizza cassette DA38 da 8mm o la Alesis (www.alesis.com) che utilizza cassette video VHS su sistemi ADAT.

Figura 12a: Strumentazione Alesis

· DAT: sono piccole cassette stereo da 4mm con durata di circa 3 ore facilmente leggibili da lettori portatili e molto maneggevoli.

Figura 11b: Cassetta audio tradizionale e cassetta DAT

· CD-Recorder: registra su un supporto CD 16 bit a 44.100 KHz a lettura

ottica. I parametri sono appena sufficienti per essere ammessi dalla normativa e il notevole consumo di corrente e la dimensione del supporto lo rendo sconsigliabile.

Figura 11c : CD riscrivibile Traxdata da 650 Mb ( 74 min )

Allo scopo di verificare l’esatta messa a punto del fonometro è indispensabile controllare periodicamente la taratura dello strumento. Un simile processo è molto importante in quanto consente di valutare l’insorgenza o la presenza di eventuali difetti di funzionamento. Generalmente il calibratore ha la forma di un cilindro con un buco in mezzo dove viene inserito il microfono. L’uso è semplicissimo: basta infilare il microfono nella cavità dello strumento impiegando gli adattatori in dotazione ed immediatamente si produce al suo interno il livello di pressione sonora costante sulla membrana del microfono. La calibrazione è prevista con un segnale di riferimento stabilizzato, ricavato da un circuito oscillatore interno, tipicamente alla frequenza di 1 KHz e di ampiezza pari a 50 mV, corrispondenti in dB a:

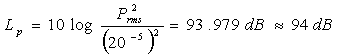
I 94 dB di livello del segnale fanno perciò riferimento a un microfono la cui sensibilità corrisponde a 50mV/Pa. Purtroppo non tutti i microfoni – anche dello stesso tipo – hanno uguale sensibilità: conseguentemente è necessario che i 94 dB di riferimento vengano opportunamente corretti in base all’effettiva sensibilità del microfono. Uno dei punti di riferimento in Italia sono i laboratori della Spectra (www.Spectra.it )

Il fonometro visto in aula è un analizzatore di spettro dotato di un DSP che mi trasforma il segnale nel dominio della frequenza e visualizzato con uno spettro in base di terzi di ottava . Il notevole vantaggio consiste in una memoria interna da 20Mb e da una porta PCMCIA in cui poter espandere il tutto a prezzi molto economici garantendomi misure lunghe e durature nel tempo.

In più, svitando il microfono, mi rendo conto della possibilità di inserirne un secondo tramite un cavetto sdoppiatore sfruttando l’ingresso bicanale dello strumento, facendo lavorare i due trasduttori per differenza.

Infine, qualora la zona delle rilevazioni fosse accidentalmente influenzata da rumore, una memoria interna mi consente di cancellare gli ultimi dieci secondi di registrazione.