Introduzione
La fisica tecnica si pone
come obiettivo di creare un collegamento tra la fisica e la tecnica.
La fisica è una scienza
esatta. Partendo da principi non dimostrati (postulati) sviluppa per successive
deduzioni l’intero complesso di proposizioni costituenti la scienza stessa. Il
complesso di proposizioni così ottenuto si definisce autofondato.
La tecnica non ha niente
di scientifico, non utilizza il metodo ipotetico-deduttivo, ma predilige metodi
più rapidi e intuitivi (es. tentativi). L’esattezza non appartiene alla tecnica
che invece ha a che fare con l’accuratezza e la precisione.
Procedimenti di astrazione

Nel mondo reale ci sono
problemi che si possono risolvere anche senza l’ausilio della fisica e della
matematica. Si può procedere con metodi empirici, questo modo di agire si
chiama soluzione diretta del problema.
Per esempio le marmitte
delle automobili e delle moto si producono per tentativi.
Non sempre è possibile
risolvere il problema in modo diretto, in questi casi si ricorre alla fisica
(si velocizza e si semplifica la soluzione) tramite un procedimento di astrazione.
Con la conoscenza della suddetta materia si risolve il problema e poi tramite l’operazione
di applicazione si ritorna al mondo reale.
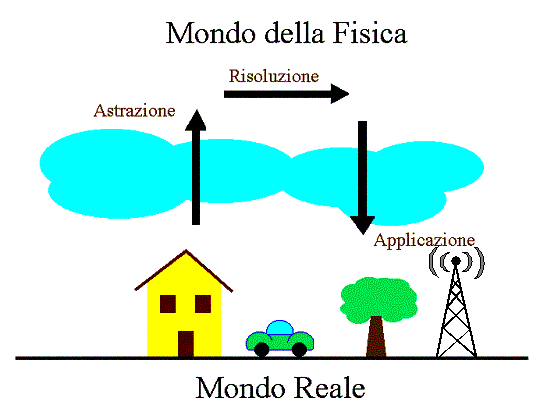
Durante l’astrazione, si vuole creare una rappresentazione della grandezza fisica (mediante l’operazione di misura) della quale si ha solo una percezione nel mondo reale.

Bisogna prestare
attenzione perché nei procedimenti di astrazione e applicazione si possono
perdere delle informazioni. Inoltre non tutte le grandezze fisiche sono
misurabili e la metodica stessa di misura può causare variabili fisiche diverse.
Per esempio solo
ultimamente la temperatura è diventata una misura univocamente riconosciuta,
prima ne esistevano diverse (celsius, termodinamica, gas perfetto).
A tutt’oggi l’odore, il
colore, l’olfatto sono grandezze fisiche non misurabili.
Una volta giunti nel
mondo della fisica si possono trattare in modo algebrico (tramite equazioni) i
risultati della misura.
Per esempio la prima
legge di Newton:
F = M .
a
è un’equazione formale.
A ogni simbolo
corrisponde una grandezza fisica che deve essere misurabile. Se ne comparisse
una non misurabile si afferma che l’equazione è fasulla.
In seguito dell’equazione
formale si passa a quella numerica in cui ogni simbolo si associa un numero e
la sua corrispondente unità di misura.

Esistono delle regole ben
precise a livello internazionale per le unità di misura.
A questo punto è utile
introdurre una gerarchia di verità:
1.
Principi
fisici: relazione superiore che
noi crediamo vera in quanto tale e che non è mai stata smentita.
2.
Leggi
fisiche: generalmente principi
declassati (es. prima legge di Newton). Le leggi fisiche sono approssimazioni a
cui tende asintoticamente il mondo reale a causa delle perturbazioni, come l’attrito.
3.
Formule
empiriche: derivano dall’evidenza
sperimentale. Sono formule che correlano bene i dati sperimentali. Bisogna
prestare attenzione perché se si esce dal campo di validità della formula i
risultati non sono più attendibili.
Non tutti i problemi, però, si risolvono con semplici operazioni algebriche, ma bisogna ricorrere a strumenti matematici superiori, come il calcolo infinitesimale, le equazioni differenziali, …
Questi strumenti
richiedono notevoli capacità, ma consentono di fare cose altrimenti impossibili.
Unità di misura
Cos’è una misura?
Si definisce misura il
procedimento mediante il quale si fa corrispondere un numero ad una grandezza
fisica. Per misurare una grandezza bisogna sceglierne un’altra della stessa
specie, da utilizzare come campione ed assegnarle valore numerico uno,
(definizione di unità di misura), quindi si vedrà quante volte l’unità di
misura è contenuta nella grandezza da misurare. Ogni grandezza fisica sarà caratterizzata
da un numero seguito da un simbolo (misura e unità).
Così facendo bisognerebbe
disporre di tanti campioni quante sono le grandezze fisiche. Per ridurre questo
numero si ricorre allora alle relazioni che legano tra loro le diverse grandezze;
si ottengono così delle unità di misura che utilizzano campioni di grandezze di
altre specie e sono dette unità derivate, per contro quali che sono definite direttamente
da un campione si dicono unità fondamentali.
Per esempio:
L = 10 m
è un’equazione perché c’è l’uguale.
L oggetto a formalismo libero che
identifica la grandezza fisica
10
numero puro
che rappresenta la ripetibilità del secondo oggetto a destra dell’uguale
m unità
di misura
E’ importante ricordare che condizione necessaria ma non sufficiente per l’esattezza di un’equazione è la sua verifica dimensionale, cioè se sostituisco alle grandezze le unità di misura deve riottenere le grandezze. Si dice che le equazioni devono essere omogenee.
Le unità di misura sono catalogate nel sistema internazionale e il loro
utilizzo è regolato a livello legale da alcune norme (UNI per l’Italia, CEN per
l’Europa, ISO internazionali).
Sistema Internazionale (SI)
E’ il sistema di più
recente costituzione (1960) ed incorpora quelli precedenti. In esso utilizzando
le relazioni che legano tra loro le diverse grandezze fisiche, si sono ridotte
le grandezze fondamentali e quindi i campioni da conservare, al numero minimo
di sette.
|
Quantità |
Unità |
|
Definizione |
|
Lunghezza
(L) |
metro |
m |
E’ la distanza percorsa dalla luce nel vuoto nel tempo di
1/299792458 secondi. |
|
Massa (M) |
kilogrammo |
kg |
Il kilogrammo è l'unità di massa
ed è eguale alla massa del prototipo internazionale, cilindro di platino
iridio, che è conservato presso il BIPM. |
|
Tempo (t) |
secondo |
s |
E’ l'intervallo di tempo che
contiene 9192631770 periodi della radiazione corrispondente alla transizione
tra i due livelli iperfini dello stato fondamentale dell'atomo di cesio 133. |
|
Corrente
elettrica (i) |
ampere |
A |
E’ l'intensità di corrente
elettrica che, mantenuta costante in due conduttori paralleli, di lunghezza
infinita, di sezione circolare trascurabile e posti alla distanza di un metro
l'uno dall'altro, nel vuoto, produrrebbe tra i due conduttori la forza di
2x10-7 newton per ogni metro di lunghezza. |
|
Temperatura
(T) |
kelvin |
K |
E’ l’unità di temperatura
termodinamica, è la frazione 1/273,16 della temperatura termodinamica del
punto triplo dell'acqua. |
|
Quantità
di sostanza (m) |
mole |
mol |
E’ la quantità di sostanza di un
sistema che contiene tante entità elementari quanti sono gli atomi in 0,012
kg di carbonio 12. |
|
Intensità
luminosa (I) |
candela |
cd |
E’ l'intensità luminosa, in una
data direzione, di una sorgente che emette una radiazione monocromatica di
frequenza 540 x 1012 hertz e la cui intensità energetica in quella direzione
è 1/683 watt allo steradiante. |
Il sistema internazionale è coerente, cioè tutte le unità di misura derivate si ottengono da quelle fondamentali tramite leggi fisiche senza fattori moltiplicativi.
Per esempio la prima legge di Newton:
F = M .
a
non è una grandezza
fondamentale ma derivata.
Dimensionalmente:
[F] = [M L/t2]
quindi unità di misura
della forza è:
1 N = 1 kg 1 m/s2
Non tutti i sistemi di
misura sono coerenti. Per esempio nel “Sistema Tecnico degli Ingegneri” (oggi
inutilizzato al contrario di quello americano):
1 kgf
= 9,81 1 kg 1 m/s2
La norma in Italia che
regola l’utilizzo delle unità di misura è CNR-UNI 10003.
Ecco degli esempi
relativi alle regole di impiego delle unità SI.
·
I nomi delle unità
sono considerati nomi comuni e pertanto si scrivono con l'iniziale minuscola,
anche se alcuni di essi derivano da nomi di scienziati (ampere, kelvin). In
questo caso però sono invariabili al plurale ed hanno come simbolo una lettera
maiuscola (per esempio A per l'ampere e K per il kelvin). Si noti che lo stesso
vale per le unità derivate che hanno un nome proprio di persona.
·
Il simbolo delle
unità si deve usare solo quando l'unità è accompagnata dal valore numerico;
esso deve essere scritto in carattere non corsivo (A e non A) dopo il
valore numerico, e non deve essere seguito da un punto (a meno che si tratti
del punto di fine periodo). Quando l'unità non è accompagnata dal valore
numerico, deve essere scritta per esteso e non con il simbolo.
·
Quando l'unità SI è
troppo grande o troppo piccola per certe misurazioni, è consigliabile usare
suoi multipli o sottomultipli. Per soddisfare le esigenze di tutti gli
utilizzatori del sistema SI, il CGPM ha stabilito un certo numero di prefissi
con nomi speciali, indicati nella sottostante tabella insiemi ai rispettivi
fattori.
|
Fattore |
Prefisso |
Simbolo |
|
1024 |
yotta |
Y |
|
1021 |
zetta |
Z |
|
1018 |
exa |
E |
|
1015 |
peta |
P |
|
1012 |
tera |
T |
|
109 |
giga |
G |
|
106 |
mega |
M |
|
103 |
kilo |
k |
|
100 |
- |
- |
|
10--3 |
milli |
m |
|
10--6 |
micro |
µ |
|
10--9 |
nano |
n |
|
10--12 |
pico |
p |
|
10--15 |
femto |
f |
|
10--18 |
atto |
a |
|
10--21 |
zepto |
z |
|
10--24 |
yocto |
y |
Il prefisso precede l'unità di misura con la quale
forma il multiplo o sottomultiplo; non può essere usato da solo, né si possono
usare due prefissi consecutivi. Si scriverà 1 nm e non 1 mmm, 1pF e non 1mmF. Il simbolo del prefisso è scritto con carattere
diritto come il simbolo delle unità, non si lasciano spazi, né s’interpone il
punto tra i due simboli:
1000000 kg = 106 kg = 1 Mkg
0,001 A = 10-3 A = 1 mA
·
Si raccomanda l’uso
di multipli o sottomultipli che diano luogo a valori numerici compresi tra 0,1
e 1000, con il criterio di scrivere soltanto le cifre significative:
L = 10,7 . 107
Mm
Esistono però delle eccezioni:
1BAR =
105 Pa (1Pa = 1N/m2)
è ammessa perché il BAR è una unità di misura molto comoda in quanto 1BAR corrisponde alla pressione atmosferica.
·
E’ obbligatorio
utilizzare le unità di misura derivate quando possibile, quindi non è corretto
scrivere:
10 kg m/s2
ma bisogna scrivere
10 N
·
La mantissa (cifra davanti
l’esponente) mi da la precisione della misura. In altro modo l’ultima cifra
significativa mi dice l’errore con cui è noto il valore della grandezza (sono
importanti anche gli zeri dopo la
virgola).
Esempio:
L = 10,000 m precisione
al mm
L = 10 km precisione al km
L = 10,000 km precisione al m
Quest’ultimo
considerazione sull’errore mi introduce ad un nuovo argomento.
Incertezza della misura
Il risultato di una
misura non coincide sempre con il “reale“ ciò che si sta misurando (questo
presuppone l’esistenza della verità).
Ci sono due concetti
fondamentali da trattare: l’accuratezza e la precisione.
Per spiegarli meglio si
può ricorrere all’aiuto di due disegni che rappresentano il tiro al bersaglio.
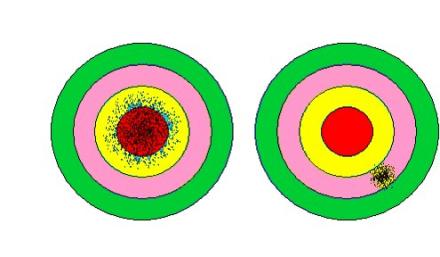
Il primo bersaglio è accurato ma non preciso, mentre il secondo è preciso ma non accurato.
L’accuratezza consiste nel misurare la distanza fra il centro del bersaglio
e i colpi. L’inaccuratezza rappresenta l’errore sistematico.
Per precisione s’intende mettere tutti i colpi vicini anche se lontano dal
centro del bersaglio. L’imprecisione è legata a l’errore casuale, che può
essere compensato con il valor medio.
Come si può intuire per valutare l’accuratezza e la precisione servono un
gran numero di prove essendo legge dei grandi numeri.
L’accuratezza e l’imprecisione sono mutuamente indipendenti.
Il ragionamento applicato al fucile si può trasferire agli strumenti di
misura.