Scambio termico per Convezione

La trasmissione del calore per convezione si verifica ogni volta che un corpo viene posto in un fluido che si trovi a una temperatura diversa da quella del corpo stesso. A causa della differenza di temperatura, si ha un flusso di calore di natura conduttiva per conduzione tra le pareti del corpo e le particelle del fluido con le quali è a contatto, provocando variazioni nella densità degli strati fluidi prossimi alla superficie. Le differenze di densità determinano il moto verso l’alto del fluido più leggero e verso il basso del fluido più pesante. In questo modo si ha un movimento di particelle verso regioni a temperature inferiori dove l’energia viene ceduta ad altre particelle. Assistiamo perciò ad un rimescolamento sia di particelle che di energia.

La situazione generica è quella di un gas a temperatura T₁ che, muovendosi, lambisce una parete, la cui temperatura è T_p, e se ne va via ad una temperatdura T₂ diversa da T₁ come in figura 1..

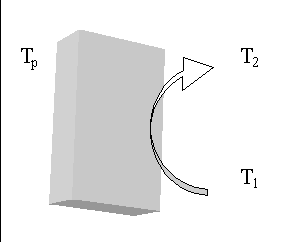
Fig. 1

In questo caso il gas asporta energia sotto forma di temperatura, pertanto, dal punto di vista del bilancio energetico, lo scambio di calore è accompagnato da una variazione di entalpia del fluido che arriva con una bassa entalpia e se ne va via ad una entalpia più alta.

La convezione avviene in modo del tutto analogo anche nei comuni termosifoni in ghisa, meglio definiti in un linguaggio tecnico come corpi scaldanti. L’aria fredda risale le lamelle ed esce calda. Il movimento è dovuto al riscaldamento stesso dell’aria che, divenendo più calda, diminuisce di densità e sale.

La trasmissione del calore per convezione si distingue in convezione naturale e convezione forzata a seconda della causa che determina il moto del fluido. Quando, come nel caso del termosifone, il movimento del fluido è dovuto esclusivamente alle differenze di densità causate dal riscaldamento, si parla di convezione naturale. Se invece il movimento è generato da agenti esterni come ventole o pompe, per esempio quella posta sulle CPU dei computer, allora la convezione si definisce forzata.

Spesso però ci si imbatte in situazioni intermedie, come accade quando si fa uso dei ventilconvettori (termosifoni con ventola). Se la ventola è in funzione l’apporto di calore all’ambiente è dovuto sia alla ventola che al termosifone stesso. In questo caso si parla di convezione mista.

In tutti e tre i casi il fluido può muoversi in modo laminare o turbolento. In generale i valori dei coefficienti di scambio di calore sono più alti nei casi di convezione forzata e moto turbolento, mentre il minimo si ha per convezione naturale e moto laminare; infatti nella convezione naturale l’intensità dei moti di mescolamento è generalmente minore rispetto alla convezione forzata.

SiccomeOccorre sottolineare come la natura del fluido influenzai molto i fenomeni di scambio termico per convezione,. lLo studio della convezione è basato sulla conoscenza delle caratteristiche fluidodinamiche del fluido.

Mettiamo a confronto due fluidi come l’aria e l’acqua.

Siccome il calore specifico dell’aria è più basso di quello dell’acqua, a parità di massa e di variazione di temperatura, l’acqua asporta più energia dell’aria e quindi è un refrigeratore migliore. E’ per questo motivo che i motori di auto e moto sono raffreddati ad acqua. Nel campo dell’elettronica, spesso, è sufficiente raffreddare ad aria; per grossi trasformatori elettrici, invece, è necessario utilizzare l’olio (data la sua elevata capacità di asportare calore) raffreddato a sua volta da un radiatore con ventola.

Dal punto di vista dell’analisi matematicaMatematicamente l’equazione di Fourier non basta per studiare lo scambio termico per convezione

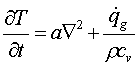
(1)

dove:

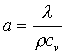
è la diffusività e è la quantità di calore scambiata per unità di volume.

Quest’equazione infatti, è stata ricavata nell’ipotesi di corpi fermi e quindi non va bene nel caso di un fluido in moto. Si può ovviare la problema sostituendo, in analogia con quanto fatto con l’equazione di Navier, la derivata parziale con quella sostanziale nella (1) ottenendo

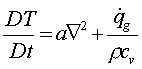
La validità di quest’equazione è garantita dall’ipotesi di moto incomprimibile; ciò significa che il lavoro di espansione che avviene quando le particelle del fluido si scaldano e diventano più leggere è trascurabile.

Supponiamo quindi che la densità sia costante, ovvero, che la sua variazione sia così piccola da essere trascurabile rispetto al valore medio .

Notiamo che questa notazione è valida solo a regime, quando le variazioni di temperature sono ormai piccole, cioè per

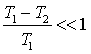
Se così non fosse, infatti, non potremmo più trascurare e quindi non sarebbe più valida l’equazione di Fourier, che vorrebbe riscritta tenendo conto dei lavori di espansione, complicando ulteriormente il calcolo.

Non sempre questa condizione è verificata; ad esempio nello studio dei fenomeni di combustione dei motori, nei sistemi a razzo e nei motori a reazione le elevate variazioni di temperatura non permettono di considerare la densità costante.

Le differenze di temperatura nel fluido innescano dei moti regolati dall’equazione di Navier. E’ per questo motivo che quest’equazione viene accoppiata alle equazioni di Fourier e di continuità in condizioni stazionarie per definire il sistema. Nei casi di convezione forzata il calcolo si può semplificare risolvendo il problema fluidodinamico e utilizzandone la soluzione come condizione al contorno del problema termico.

Ciò nonostante, nella realtà, non si riesce a risolvere questo sistema di equazioni tanto che risulta più conveniente l’utilizzo di altri metodi.

Coefficiente di Convezione

La convezione può essere quantificata usando un coefficiente di convezione definito dalla relazione empirica

La quantità Dove rappresenta il flusso di calore, la temperatura della superficie solida e è la temperatura del fluido (in un punto lontano dalla superficie).

Si nota immediatamente che questa definizione non è corretta in quanto è definito come “coefficiente” pur non essendo una grandezza adimensionale

Il coefficiente di convezione non è una quantità costante ma dipende dalla geometria della superficie, dalla velocità, dalle proprietà fisiche del fluido e spesso anche dalle differenze di temperatura.

Tuttavia, volendo conoscere la potenza complessiva scambiata, risulta più comodo introdurre il suo valore medio

dove abbiamo definito con la superficie della parete solida e con la quantità di calore scambiata.

è dato dalla relazione

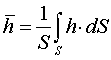
Prende il nome di coefficiente di convezione medio (o valore integrale del coefficiente di convezione).

Risolvere un problema di convezione significa ricavare il valore di .

Ciò però non può essere fatto risolvendo analiticamente le equazioni differenziali che governano il fenomeno (equazioni di Fourier e Navier).

Il coefficiente di convezione medio si ricava dalla Analisi Dimensionale

Analisi dimensionale ( o teoria dei modelli)

L’analisi dimensionale è una scienza che studia i fenomeni delle analogie. Essa si basa sul principio secondo il quale se due fenomeni fisici sono descritti dalle stesse equazioni differenziali in forma dimensionale ed hanno uguali condizioni al contorno allora avranno anche lo stesso risultato.

Infatti una equazione matematica scritta con variabili adimensionate risulta indipendente dal problema fisico considerato e perciò può essere utilizzata per descrivere una moltitudine di fenomeni. La soluzione, che è adimensionale, può essere ricavata una sola volta ed applicata via via a tutti quei casi che hanno la stessa equazione differenziale scritta con variabili adimensionali.

Il fondatore di questa teoria fu lo scienziato britannico Osborn Reynolds. Egli riuscì a dimostrare sperimentalmente l’equivalenza di risultati dei fenomeni di scambio termico, diffusione gassosa e moto dei fluidi.

La teoria dei modelli si basa sulla procedura standard che vale per tutti i fenomeni.

Il primo passo è quello di definire delle grandezze adimensionali.

Ad esempio, per analogia quanto fatto in fluidodinamica con il calcolo della velocità adimensionale, possiamo supporre di adimensionalizzare la temperatura usando la definizione di strato limite.

Consideriamo a tal fine una parete orizzontale ed un profilo di temperature piatto e incidente come in figura 2.

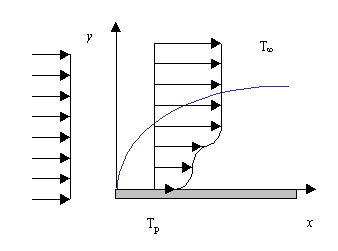
Fig. 2 – Strato termico limite

Definiamo con strato limite termico il luogo dei punti tali che la differenza di temperatura è il 99% della variazione totale di temperatura tra i punti della parete a temperatura e i punti sufficientemente lontani a temperatura .

Per calcolare la temperatura adimensionale dovrò calcolare un rapporto tra temperature. Volendo mantenere l’analogia con la velocità adimensionale, definiamo in modo che per tutti i punti dello strato limite sia 0,99; sulla lastra sia 0 e all’infinito sia uguale a 1

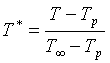
Dalla figura 2 notiamo che all’interno dello strato limite il profilo delle temperature non è necessariamente parabolico.

Il secondo passo è quello di ricavare la soluzione da un problema fluidodinamico equivalente già noto.

Si potrebbe pensare perciò di ripetere il ragionamento anche per il coefficiente di convezione. In realtà non esistono analogie per la soluzione di un problema di scambio termico convettivo, occorre fare ricorso ad un noto teorema dell’analisi dimensionale.

Teorema π (o teorema di Buckingham)

Il teorema di Buckingham permette di ricavare il numero di gruppi adimensionali indipendenti necessari ad esprimere le relazioni che descrivono un fenomeno.

Secondo questo teorema la soluzione di un’equazione fisica dimensionalmente omogenea è sempre esprimibile nella forma

Dove , , … sono i raggruppamenti adimensionali indipendenti ottenibili con le variabili e le costanti che compaiono nell’equazione da risolvere. Inoltre il numero di raggruppamenti adimensionali indipendenti è uguale al numero di variabili adimensionate che descrivono il fenomeno meno il numero di equazioni che le legano tra loro.

Supponiamo ad esempio di avere un sistema descritto da tre variabili adimensionate , A, B e C , ognuna delle quali può assumere valore tra 0 e 1 (se così non è applichiamo la dovuta adimensionalizzazione).

Se non fossimo capaci di risolvere il problema fisico dovremmo fare degli esperimenti e verificare, successivamente, la correttezza dei risultati. Potremmo perciò prendere, per ogni variabile, 10 possibili valori nell’intervallo [0,1], fare i dovuti esperimenti e alla fine verificare i risultati con le equazioni in possesso. In questo modo il numero di esperimenti che dovremmo compiere sarebbero 1000 (infatti abbiamo 10 possibili discretizzazioni per ognuna delle variabili). Quindi, in generale, dato un problema fisico che non si può risolvere analiticamente, dovrei ricorrere a miliardi di esperimenti per poter vagliare la variabilità e la dipendenza di tutte le possibili variabili.

Ma s; supponiamo inoltre che esistano due relazioni che le legano

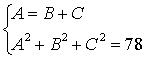
In presenza di tre variabili e due relazioni di legame, secondo il teorema, abbiano 1un raggruppamento adimensionale indipendente. Quindi la soluzione di questa ipotetica equazione è del tipo

Dove è espresso da A, B , e C . In presenza di un solo gruppo adimensionale il numero di esperimenti si ridurrebbe a 10 e non puù 1000.

Occorre però fare molta attenzione. Il teorema dice quanti siano i raggruppamenti indipendenti ma non quali siano. Perciò se ricaviamo che esistono un certo numero di variabili indipendenti in realtà bisogna fare ricorso alla fisica del problema o all’analogia di Reynolds per capire quali scegliere.

Ciò sta alla base del calcolo del coefficiente di convezione.

Supponiamo di cercare la soluzione del problema convettivo più complesso possibile che è quello quindi di porci in condizioni di convezione mista e moto turbolento (che è il caso più generico in cui compaiono convezione mista e convezione forzata) e di voler cerchiamo di calcolare locale (infatti la scelta del valor medio abbasserebbe di uno il numero di variabili adimensionali introducendo una nuova equazione). Il teorema ci viene in aiuto dicendo che i numeri primi indipendenti (gruppi adimensionali) sono quattro.

Se prendiamo un numero superiore di variabili quelle in eccesso saranno esprimibili in funzione delle prime quattro.;

perciò, Adimensionalizzando le 5 equazioni ( 3 equazioni di Navier, 1 di Fourier e 1 di continuità) escono scegliendo 5cinque variabili adimensionali. Perciò, siccome dal terorema di Buckingham avevamo trovato 4 variabili indipendenti, esisterà una relazione formale che esprime la quinta variabileuno di questi numeri in funzione degli altrille altre.

Tradizionalmente sSii predilige prendere come variabili indipendenti i numeri puri:

Nu, Re, Gr, Pr,

e come numero dipendente dagli altri il numero di Nusselt Nu, da cui la relazione di legame

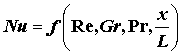
cheIl numero di Nusselt esprime il coefficiente di convezione adimensionato. Esso non può assumere valori arbitrari ma, fissati gli altri raggruppamenti, esso vale

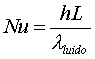(2)

dove L rappresenta la lunghezza caratteristica del problema, h il coefficiente di convezione locale e la conducibilità del fluido.

A questo punto per ricavare il coefficiente di convezione basta trovare il legame funzionale e sostituirlo nella (2) al posto di Nu.

Queste funzioni, tabellate sui libri, sono state ricavate sperimentalmente negli anni ’30 – ’40 dai tedeschi.

La loro formula generica è

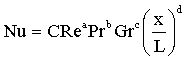
Dove la costante C e gli esponenti a,b,c,d, sono da determinare in base alla particolare situazione geometrica, termica e dinamica.

La variabile adimensionale indipendente si chiama ascisssa asimensionale ed è un parametro addizionale in cui figurano la coordinata x e la lunghezza caratteristica L; esso mi dice in che punto della mia geometria mi trovo. La scelta di Lquest’ultima è estremamente importante. Potremmo dare diverse definizioni di L a seconda del problema in cui ci troviamo; ad esempio, per un fluido che scorre in un tubo, la lunghezza caratteristica potrebbe essere il diametro del tubo, ma ci sono casi in cui potrebbe essere anche il diametro del tubo. Quindi L non è sempre la stessa e per lo stesso problema si potrebbe attribuirne significati diversi. E’ necessario però che la scelta che facciamo sia concorde con quella che ha fatto lo sperimentatore nel definire il formulino. In caso contrario la teoria dei modelli non sarebbe più applicabile.

Si nota inoltre la ristretta gamma di validità di questa formula che, proprio per legami di tipo unicamente esponenziale, è utilizzabile solo per alcuni tratti.

Numeri puri e significato fisico

Il numero primo Re è il numero di Reynolds. Esso è espresso dalla relazione:

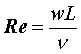
dove: w è la velocità media con cui viene spinto il fluido. In convezione naturale w = 0, quindi il numero di Reynolds non dà nessun contributo al formulino.

n è la velocità cinematica e si misura in m²/sec

In pratica Re esprime il rapporto tra le forze d’inerzia (quantità di moto) e le forze di attrito viscoso.

Il secondo numero è il numero di Grashof

.

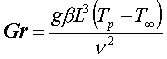
dove g è l’accelerazione di gravità e b è il coefficiente di dilatazione termica.

Il numero di Grashof esprimeDefinisce il rapporto tra le forze di galleggiamento (ascensionali) e le forze viscose.

Il “coefficiente” b\ \indica la variazione di volume specifico in rapporto alla variazione di tempo a pressione costante e si chiama coefficiente di dilatazione termica

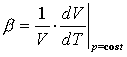(3)

Dove V è il volume e T è la temperatura.

Per un gas perfetto vale la relazione

da cui, ricavando * e sostituendo in (31) ottengo

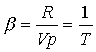
Qunidi b si misura in

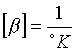
Ciò, chiaramente, non valesi puòo’ fare anche per i liquidi i cui coefficienti di dilatazione termica sono però tabellati sui libri. Per esempio nell’acqua tra 0 e 4 °C b\\ è negativo perché al crescere della temperatura il volume dell’acqua aumenta. A rigore b\\ dovrebbe essere preso in valore assoluto; in realtà i suoi valori sono sempre positivi eccetto appunto casi come l’acqua.

L’ultimo numero, Pr, è il numero di Prandtl ed è definito dalla formula

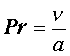
dove con a abbiamo indicato la diffusività, spesso indicata anche con \\a²

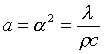
Con c chiamiamo il calore specifico ed in particolare useremo c_p (calore specifico a pressione costante) per i gas.

Dal punto di vista fisico questo numero esprime l’importanza che ha la diffusione delle forze di attrito rispetto alla diffusione termica intendendo per diffusione una propagazione spaziale.

In sostanza Pr indica la tendenza di un fluido a trasportare quantità di moto piuttosto che calore.

Consideriamo per esempio il calcolo dello strato limite per la lastrina. La sua altezza dipende dalla diffusività. Può accadere che lo strato limite termico non coincida con quello dinamico, come si nota dal diagramma in figura 3. Ciò dipende dal rapporto delle diffusività \\ e quindi dalla prevalenza o meno di forze di attrito.

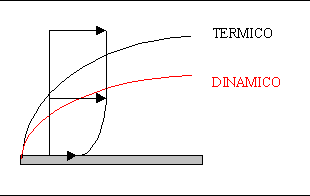
Fig. 3 – Strato limite dinamico e termico

Se \\<1, i punti del fluido che stanno tra lo stato termico limite e quello dinamicoal di fuori dello strato termico limite risentiranno del cambiamento della temperatura, dovuta alla vicinanza della parete, ma e non ancora del cambiamento di velocità. Quindi il numero di Prandtl ha un preciso significato fisico; esso ci dice, come in questo caso, quanto lontano dalla parete si sentono la perturbazione termica e la perturbazione dinamica.

In generale, se Pr<1<1 prevale l’effetto di diffusione termica, mentre, se Pr>1 prevale l’effetto dinamico.

L’azione della diffusività termica si vede meglio se analizziamo l’imbocco di un condotto.

Supponiamo di avere un profilo di temperature uniformi (T_¥) di un fluido che imbocca un tubo in prossimità di un imbocco, ad esempio il tubo di scarico di un serbatoio, con una certa velocità u. Supponiamo che le pareti del tubo siano a temperatura T_p , come in figure a 4 e 5, in modo da avere un3, in modo da avere uno scambio termico di tipo convettivo

Preso un punto all’interno del condotto, la sezione trasversale del tubo passante per quel punto sarà sede di un profilo di temperature variabili con la diffusivitào scambio termico di .tipo convettivo.

Preso un punto all’interno del condotto, la sezione trasversale del tubo passante per quel punto sarà sede di un profilo di temperature variabili con la diffusività. Si nota subito che il nocciolo centrale del fluido nel tubo sarà meno soggetto alle variazioni di temperatura. In particolare all’aumentare della diffusività gli effetti di scambio termico saranno più rapidi e quindi il liquido risentirà subito della perturbazione di temperatura (dovuta alle pareti), anche in punti più vicini all’imbocco.

Viceversa se la diffusività diminuisce, il fluido continuerà a scorre senza risentire della presenza della parete e i punti a subire degli effetti della perturbazione saranno più lontani.

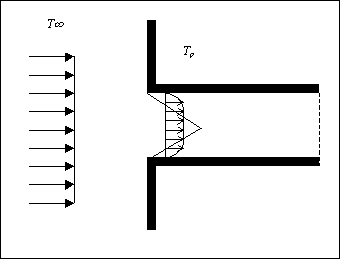
Fig.4 – effetti a diffusività maggiore

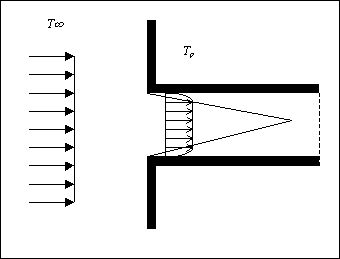
Fig.5 – effetti a diffusità inferiore

La diversità si spiega bene nei disegni riportati; per una alta diffusività, figura 4, lo strato limite è poco allungato e quindi è maggiore l’effetto parabolico del profilo delle temperature nel tubo; a diffusività minore, figura 5, lo strato limite si allunga e perciò sulla stessa sezione di tubo notiamo che l’effetto parabolico è minore, cioè sono minime le variazioni di temperatura.

Mettiamo a confronto i valori della diffusività nell’acqua e nell’aria

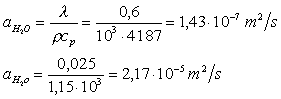
Possiamo concludere che lo strato limite termico in aria si realizza più velocemente che in acqua.