Esercizi di scambio termico per convezione

UNIVERSITA’ DEGLI STUDI DI PARMA

Anno accademico 2000-2001

Corso di laurea : ingegneria delle telecomunicazioni

Corso di fisica tecnica

Docente del corso : Angelo Farina

Relazione della lezione di fisica tecnica tenuta il giorno 12/12/2000 alle ore 16 :30-18 :30

RICHIAMI DI TEORIA

Gran parte dei fenomeni legati allo scambio termico fra corpi per via convettiva può essere studiato calcolando il coefficiente di convezione h dato dalla relazione

(1)

A tal scopo è necessario conoscere il numero di Nusselt Nu che nel caso più generale può essere ricavato tramite una formula del tipo

(2)

Esistono però alcuni casi in cui l' espressione risulta semplificata di alcuni termini:

1- Quando il regime è sviluppato, cioè quando la regione d' ingresso può considerarsi esaurita scompare la dipendenza dal parametro posizionatore

2- Nel caso di convezione forzata pura sono trascurabili le forze di galleggiamento, quindi si trascura il parametro Gr

3- Nel caso di convezione naturale pura sono ininfluenti le forze d' inerzia, quindi scompare il termine Re

4- Se la convezione naturale riguarda un gas perfetto su una superficie indefinita ( ad esempio aria che si trova ad una temperatura inferiore rispetto al pavimento di una stanza) il coefficiente h non dipende da L ( la lunghezza caratteristica) che assume un valore di comodo 1m. In queste condizioni Nu risulta

(3)

Analiticamente si ottiene:

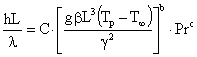(4)

Si osserva quindi che perché L scompaia dall' equazione si deve avere b=0.33, infatti solo questo valore verifica la relazione (L³ )^b=L.

Se il moto del fluido è altresì laminare si pone b=c, ottenendo così un nuovo numero detto numero di Rayleigh Ra=Gr∙Pr.

Il numero di Nussel si esprime allora nella forma Nu=C.Ra

Un caso simile si verifica nel caso di convezione forzata e moto laminare in cui si pone a=c e si definisce il numero di Plecect: Pe=Re.Pr , Nu=C.Pe

Nella pratica, una volta calcolati i numeri di Pr e Gr si calcola Ra, dopodichè si consulta una tabella che restituisce i parametri a, b, c in base al valore di Ra ed alla geometria del sistema. Un esempio di tabella è la seguente:

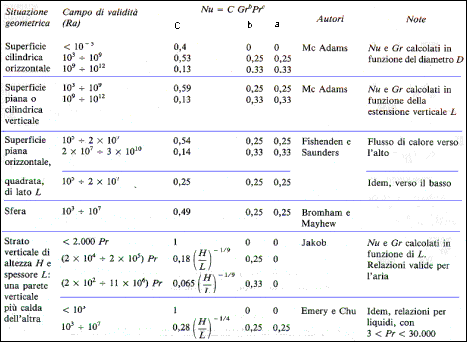
Tab.1- Formule sperimentali per il calcolo del numero di Nusselt

ESERCIZIO 1

Consideriamo un condotto a sezione rettangolare al cui interno è presente aria ferma soggetta a convezione naturale. La parete inferiore è adiabatica, mentre le altre sono rispettivamente alle temperature T₁, T₂, T₃. Si vuole determinare la temperatura T_i dell' aria.

N.B. la domanda può apparire malposta, in realtà si chiede la temperatura media riferita alla massa d' aria.

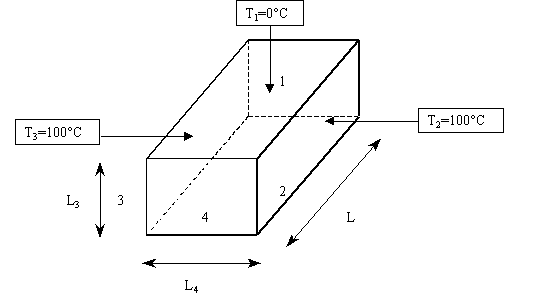
Fig.1- Scatolone adiabatico

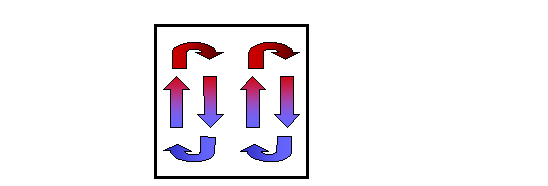
Fig.2- Moti convettivi all' interno di un condotto

Schematizziamo i dati facendo riferimento alla fig.1

L₁=L₄=2m

L₂=L₃=1.5m

T₁=0°C

T₂=T₃=100°C

Risoluzione

Ricordando l' andamento del moto dell' aria nel condotto a causa della sola convezione naturale come mostrato in fig.2, possiamo procedere alla risoluzione utilizzando la teoria dei modelli.

Il problema si riduce quindi allo studio di una rete elettrica come quella di fig.3 in cui le correnti rappresentano il flusso del calore Q, le tensioni ai nodi le temperature T₁, T₂, T₃ e le resistenze sono le resistenze termiche R₁, R₂, R₃. Ovviamente le resistenze termiche sono tre poiché sono tre le pareti che scambiano calore: R₁ è dovuta allo scambio con la parete superiore, mentre R₂ e R₃ allo scambio con le rispettive pareti laterali.

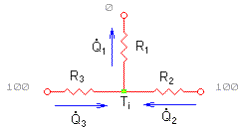
Fig.3- Rete elettrica equivalente

Dato che T₂ e T₃ sono uguali le due resistenze R₂ e R₃ possono essere considerate in parallelo, quindi la rete può essere semplificata notevolmente (fig.4).

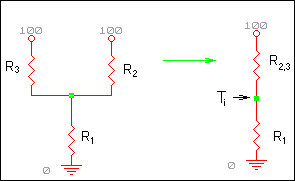
Fig.4- Rete elettrica semplificata

Per risolvere l' esercizio è necessario conoscere le superfici S e i coefficienti di convezione h₁ e h₂.

Notiamo che poiché siamo in regime di convezione naturale le superfici sono subito note: si pone infatti L=1m e si ottiene

S₁=1.5m.L

S₂=2m.L

Per ricavare i coefficienti di convezione dobbiamo passare attraverso il calcolo del numero di Nusselt

Nu=C.Gr^a.Pr^b (5)

Rifacendoci alla tabella 1 nell' ipotesi di superficie orizzontale piana e di moto turbolento (Ra>10⁹) secondo le formule sperimentali di Fishenden e Saunders otteniamo due possibili valori di Nu ( ricordando che Ra=Gr.Pr) a seconda della parete considerata.

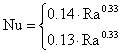(6)

Non resta quindi che calcolare il numero di Grashof che è definito come

(7)

Notiamo però che all' interno della sua espressione è presente l' incognita T_i. E' quindi opportuno procedere per tentativi, assegnando un valore ragionevole a T_i e riprovando con un valore differente nel caso in cui il risultato si discostasse troppo da quello ottenuto utilizzando una formula differente per la verifica.

Scegliamo come valore di primo tentativo T_i^*=60°C

(la viscosità cinematica dell' aria a 60°C è 1.89∙10^-5 )

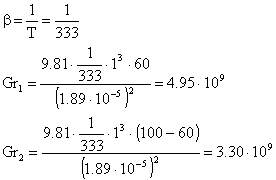(8)

Pr per l' aria alla temperatura T_i^*=60°C è 0.71, quindi possiamo ricavare i due valori cercati del numero di Rayleigh:

Ra₁=3.51.10⁹

Ra₂=2.34.109

Entrambi i valori rientrano nel campo di validità di Ra, per cui si può sostituire e ricavare Nu

(9)

Dalla relazione

(10)

Si ricavano i due coefficienti di convezione

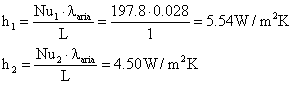(11)

A questo punto abbiamo tutti gli elementi necessari per risolvere la rete elettrica: si tratta di un partitore di tensione che si può risolvere con la nota formula

(12)

Ottengo

(13)

La T_i ottenuta si discosta però dal valore di 60°C scelto come primo tentativo, quindi sarebbe opportuno ripetere gli stessi calcoli partendo da un valore, ad esempio di T_i**=55°C

I valori così ottenuti sono:

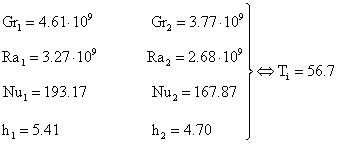(14)

Esercizio 2

Isolamento anticondensa di una tubazione

Si consideri un condotto di acciaio di sezione circolare dentro il quale scorre acqua ad una temperatura inferiore a quella dell’ ambiente. Si vuole determinare la dimensione dell’ isolante da porre all’ interno del tubo per impedire che l’ acqua condensi e provochi l’ arrugginimento del metallo.

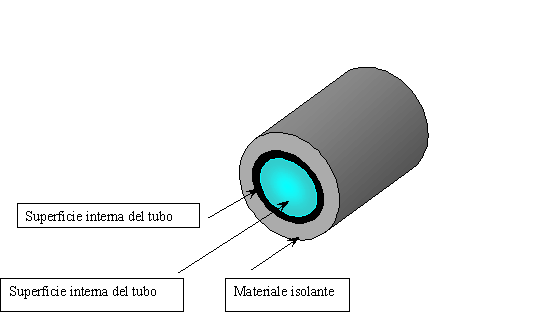
Fig.5- Tubo metallico rivestito di isolante

Dati del problema

R₁=13mm

R₂=17mm

T_acqua=5°C

T_aria=20°C

w_aria=0.5

Facendo riferimento al diagramma psicometrico seguente si determina la temperatura di rugiada Tr=10°C. E’ infatti ragionevole supporre che la temperatura esterna del tubo non si discosti molto dai 5°C dell’ acqua con la conseguente formazione di rugiada per il contatto dell’ aria più calda con questa superficie fredda. Per evitare questo inconveniente è allora necessario che la temperatura esterna dell’ isolante non sia inferiore a 10°C.

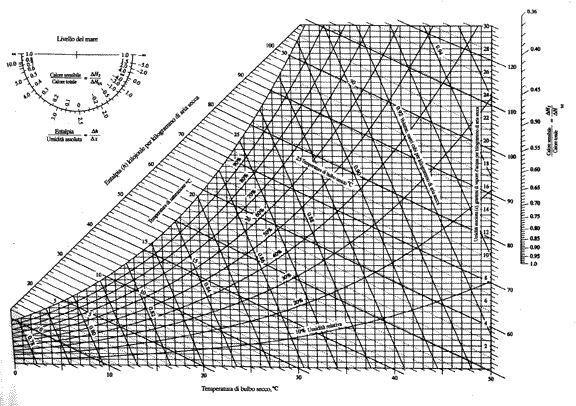
Fig.6- Diagramma psicrometrico a pressione atmosferica

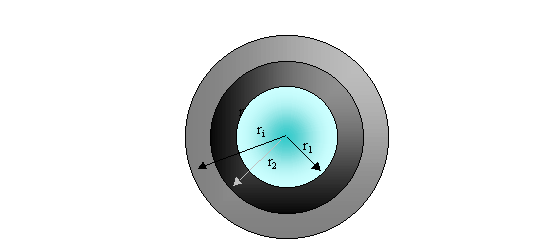
Fig.7- Sezione del tubo

Per completare lo studio del problema supponiamo che l’ acqua abbia una velocità w=1m/s e che si utilizzi come isolante del poliuretano espanso:

l_i=0.04W/mK

l_acciaio=75W/mK

Risoluzione

Anche in questo caso il metodo di risoluzione più semplice consiste nello studio della rete elettrica equivalente.

Studiando il problema dal punto di vista termico si trovano quattro resistenze termiche in serie poste tra le tensioni T_acqua e T_aria.

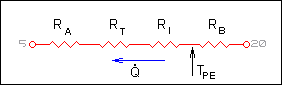
Fig.8- Rete elettrica equivalente

convezione forzata all’ interno del tubo

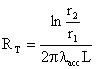conduzione attraverso lo spessore d’ acciaio

conduzione attraverso lo spessore di isolante

convezione naturale esterna a tubo e rivestimento

Ponendo ancora una volta L=1m si può ricavare la potenza termica scambiata:

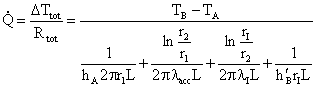(15)

Si può quindi utilizzare questa potenza ( non richiesta in precedenza) per ricavare la tensione incognita Tpe operando sull’ ultima resistenza:

(16)

Si procede ancora una volta per tentativi, ipotizzando un valore plausibile del raggio dell’ isolante: r_i*=20mm

Notiamo che sono presenti due tipi di convezione:

1- Acqua Þ convezione forzata

2- Aria Þ convezione naturale

1- si studia utilizzando l’ equazione di Dittus-Boelter per cui

Nu=0.023.Re^0.8.Pr^0.4

Tab2- Formule sperimentali per il calcolo del numero di Nusselt: convezione forzata

N.B. si pone 0.4 come esponente perché il fluido sta venendo riscaldato, altrimenti si sarebbe dovuto porre 0.3.

Si calcola immediatamente Re utilizzando il valore della velocità e della viscosità dell’ acqua a 5°C:

(17)

Notiamo che Re>10000, quindi il moto è turbolento.

Dalle tabelle si ricava Pr per l’ acqua a 5°C: Pr_5°C=12.2

Quindi otteniamo

Nu=0.023.17000^0.8.12.2^0.4=152

Ricordando che ricaviamo il coefficiente di convezione

(18)

E’ possibile così calcolare facilmente R₁, R₂ e R₃ ( R₁ e R₂ assumono comunque valori trascurabili)

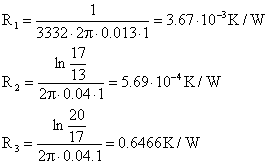(19)

Resta da calcolare solo R₄: in questo caso

Nu=0.53Gr^0.25Pr^0.25

Bisogna calcolare Gr ricordando che bisogna svolgere i conti sul diametro dell' isolante D=0.04m

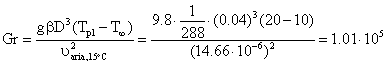(20)

Il valore di Ra che si ricava in questo modo è <<10⁹, per cui ci si trova senz' altro in condizione di moto laminare.

Sostituendo

(21)

(22)

Maggioriamo il coefficiente h_b per tener conto della componente di irraggiamento dello scambio termico, per cui

(per una maggiore precisione fare riferimento alla lezione del 18/12/00)

Si ottiene così

(23)

Sommando le 4 resistenze si ricava la resistenza termica totale

R_tot=1.44661K/W

A questo punto è semplice ricavare la potenza totale scambiata

(24)

Per ricavare la temperatura della parete esterna si sfrutta la relazione

(25)

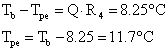(26)

In questo caso non è necessario ripetere i calcoli per un altro valore dello spessore di isolante; 3mm è infatti un spessore tipicamente reperibile in commercio: il calcolo di un valore più preciso (ad es. 2.8mm) non avrebbe quindi nessuna utilità pratica.