Argomenti trattati
Strumenti di misura della velocità di un fluido
(continua dalla lezione precedente)
Esercizi sul moto dei fluidi
Appendice
Strumenti di misura della velocità di un fluido
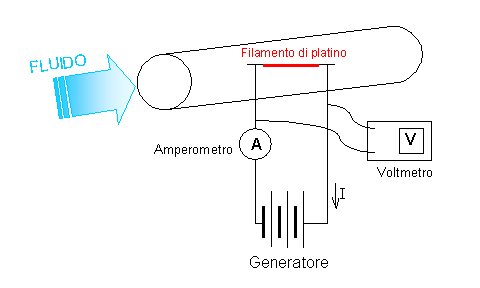
Questo strumento è un misuratore puntuale di velocità. Il suo principio di funzionamento si basa sullo scambio di calore che avviene tra il filamento di platino in cui circola corrente e il fluido che attraversa il tubo.

Fig. 1 – Anemometro a filo caldo.
All’interno del tubo viene teso un filo di platino nel quale viene fatta passare una corrente I. Utilizzando un voltmetro e un amperometro misuriamo il rapporto fra la tensione ai capi del filo D V e la corrente I; riusciamo così a conoscere il valore della resistenza elettrica R:
![]() (1)
(1)
Sappiamo anche che la resistenza elettrica di un conduttore ohmico dipende in modo lineare dalla temperatura:
![]() (2)
(2)
Quindi siamo in grado di determinare la temperatura del filo Tfilo.
Inoltre dal prodotto D V * I sappiamo il calore dissipato per effetto Joule per unità di tempo; dalle relazioni sullo scambio termico si ha:
![]() (3)
(3)
Ove Sfilo è la superficie del filo, D
T è la differenza di temperatura tra il filo e la temperatura del fluido ad un’adeguata distanza, mentre h è l’unica incognita che possiamo così determinare. h, che viene chiamato coefficiente di convezione, è funzione di alcuni parametri tra cui la velocità del fluido W. Solitamente il legame tra h e W non è lineare; esistono delle opportune tabelle però che permettono di conoscere h sapendo il valore del rapporto ![]() .
.
L’anemometro a filo caldo è collegato a degli strumenti elettronici che hanno in memoria le tabelle necessarie al calcolo di h. In questo modo lo strumento riporta direttamente come valore in uscita la velocità del fluido.
Questo anemometro presenta il vantaggio di essere piuttosto piccolo se confrontato con altri trasduttori di portata, è quindi utilizzabile in condotti stretti, anche se le ridotte dimensioni del filo di platino lo rendono molto fragile.
Questo strumento è un misuratore puntuale di velocità basato sul fenomeno dell’interferenza e sull’effetto Doppler. Il tipo di radiazione elettromagnetica utilizzata è la luce laser.
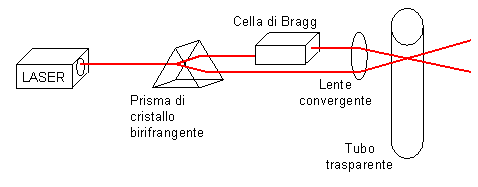
Fig. 2 – Percorso della luce laser.
Lo strumento è costituito da una sorgente laser che produce un fascio coerente (cioè tutti i fotoni mantengono una differenza di fase costante fra loro) che viene sdoppiato da un cristallo birifrangente (cioè con due indici di rifrazione) in modo da avere a disposizione due fasci coerenti. Uno dei due fasci subisce uno shift in frequenza (cioè viene portato ad una frequenza pari a 40 MHz) passando in una Cella di Bragg; infine i due raggi passano in una lente convergente che focalizza il fascio in un punto interno al condotto in cui voglio misurare la velocità W del fluido. 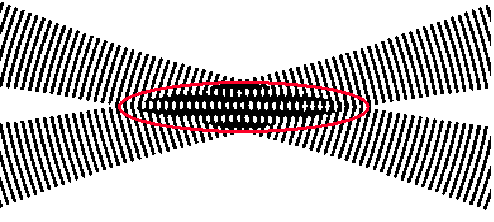
Fig. 3 – Frange di interferenza della luce laser nel punto di incidenza dei due raggi
Nel punto di intersezione si hanno fenomeni di interferenza. Significa che nascono frange chiare e frange scure (cioè luoghi distinti in cui vi è luce e in cui vi è buio che si alternano fra loro); è importante notare che siccome i due raggi diversa hanno diversa frequenza si potrà osservare un costante movimento delle frange in un determinato verso.
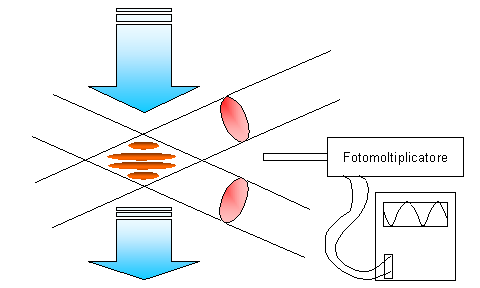
Fig. 4 – Zona di interferenza del laser nel tubo
Il fluido transita nel tubo in direzione normale rispetto al piano formato dalle frange di interferenza. Se il tubo in cui transita il fluido è trasparente alla luce laser e il fluido è trasparente e contenente delle particelle o polveri fotoluminescenti (capaci cioè di emettere luce quando illuminate) quando queste passano attraverso una frangia chiara riflettono la luce, generando così un impulso luminoso, mentre quando attraversano la frangia scura non danno luogo a riflessione.
Un fotomoltiplicatore è un trasduttore fotonico-elettrico cioè uno strumento in grado di trasformare gli impulsi luminosi che riceve in impulsi elettrici. Se, utilizzando un opportuno gruppo di lenti, focalizziamo il fotomoltiplicatore nel punto in cui i due fasci laser si incontrano possiamo misurare, collegando il fotomoltiplicatore ad un oscilloscopio, il tempo D t fra due distinti impulsi luminosi emessi dalla particella fotoluminescente. Otteniamo quindi la frequenza n di emissione con la nota formula:
![]() (4)
(4)
Per il corretto funzionamento dello strumento la Cella di Bragg è indispensabile. Se il fluido nel condotto fosse fermo, le particelle fotoluminescenti non attraverserebbero le frange chiare e quindi non si avrebbe emissione di impulsi luminosi di alcun tipo. Grazie alla differenza di frequenza di 40 MHz tra i due fasci dovuta alla Cella di Bragg invece le frange di interferenza si muovono e con il fotomoltiplicatore misuriamo una frequenza u 0 di 40 MHz.
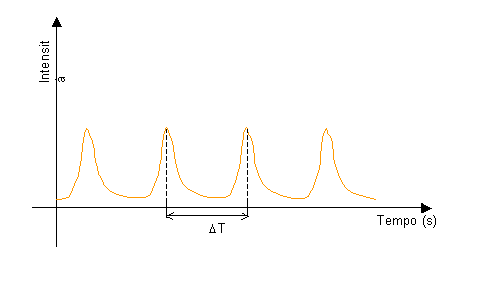
Fig. 5 – Emissioni luminose rilevate dal tubo fotomoltiplicatore (senza shift in frequenza di uno dei due raggi)
Senza l’effetto della Cella di Bragg non si riuscirebbe nemmeno a determinare il verso del movimento del fluido nel condotto. Quando il fluido è in movimento si ha l’effetto Doppler dovuto al contemporaneo movimento sia del fluido che delle frange: se la frequenza n
di emissione degli impulsi luminosi dovuti alle particelle è maggiore di 40 MHz significa che la particella fotoluminescente e quindi con essa il fluido si sta muovendo in senso opposto rispetto al verso di scorrimento della frange. Dalla misura di n
si riesce a risalire alla velocità W del fluido in quanto essa è proporzionale a n
. Più precisamente, un volta nota la distanza d tra due frange di interferenza la velocità è ![]() .
.
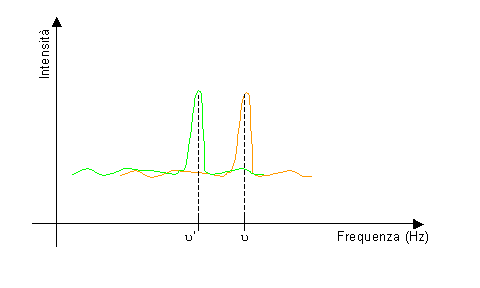
Fig. 6 – Emissioni luminose rilevate dal fotomoltiplicatore (utilizzando la Cella di Bragg); fluido in moto (u ’) e fluido fermo (u = 40 MHz).
Purtroppo questo dispositivo è molto costoso e funziona solo con fluidi trasparenti, nei quali è possibile introdurre particelle fotoluminescenti, e che possono essere contenuti in tubi anch’essi trasparenti ai raggi laser.

Fig. 7 –Un esempio di anemometro prodotto dalla Dantec che misura la velocità del fluido all’interno di un tubo trasparente.
Nonostante questi svantaggi è uno strumento di altissima precisione nella misura della velocità, che non richiede calibratura e che riesce ad analizzare un’area ristrettissima (praticamente puntiforme) del condotto, quindi dotato di un’altissima risoluzione spaziale, poiché la misura viene effettuata nel punto d’intersezione dei raggi laser. Infine è da notare come appunto grazie alla natura stessa della radiazione luminosa il flusso che viene esaminato non viene contaminato in alcun modo.
- Misuratore ad effetto Coriolis
Questo strumento è un misuratore di portata che sfrutta l’effetto Coriolis (forza apparente dovuta alla rotazione terrestre).
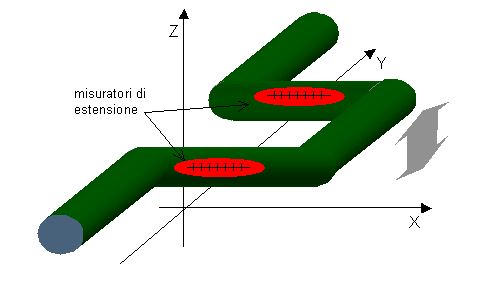
Fig. 8 – Trasduttore ad effetto Coriolis
Il misuratore di portata ad effetto Coriolis si realizza aggiungendo al condotto un percorso "a ferro di cavallo" parallelo al piano xy ed al vertice dello stesso viene posto un vibratore che ha il compito di fare oscillare il condotto lungo l’asse z mentre è attraversato dal fluido.
Per rispettare la conservazione della quantità di moto, a causa dell’effetto Coriolis, si ha una coppia di forze costante che torce il condotto.
Da equazioni fisiche sappiamo che la velocità W del fluido è proporzionale alla coppia di torsione; quest’ultima è facilmente misurabile per mezzo di misuratori di estensione posizionati sulle braccia del condotto. Questi strumenti sono dei trasduttori che collegati a degli apparecchi elettronici rendono possibile la lettura del valore di portata del condotto. Prima di utilizzare questo strumento è necessario tararlo inserendo momentaneamente nel condotto un altro misuratore di portata.
Questo tipo di misuratore di portata è molto usato in ambito industriale, non richiede di essere ritarato al variare del fluido che circola nel condotto ed è un sistema piuttosto economico.
Gli svantaggi di questo trasduttore sono legati all’effetto Coriolis: infatti questo effetto è nullo ai poli e all’equatore. Quindi questo strumento non può essere utilizzato ovunque. In particolare lo strumento è maggiormente sensibile alle latitudini intermedie dove l’effetto Coriolis è più accentuato.
Esercizi sul moto dei fluidi

Breve introduzione: l’autoclave
Un’autoclave, che sarà l’oggetto di questo primo esercizio, è un recipiente in cui si possono raggiungere pressioni elevate che di solito contiene liquido a temperature elevate. Un caso particolare può essere quello degli impianti di riscaldamento che contengono acqua calda. In questi impianti l’acqua scaldandosi diminuisce di volume e diminuisce la pressione dell’aria. In questo modo si corre il rischio di non riuscire a rifornire i piani superiori con l’acqua calda. E’ quindi necessario ripristinare la pressione iniziale con una pompa. Appena la pressione nell’autoclave diminuisce la pompa viene azionata in modo da ripristinare pressione iniziale e il volume iniziale di acqua.
Testo
Data un’autoclave collegata ad un recipiente aperto tramite un tubo su cui è installata una pompa determinare la prevalenza D
p e la potenza P della pompa tale che mantenga una portata in massa ![]()
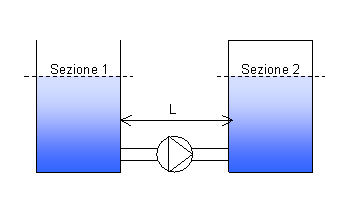
Dati
P1= 1 bar = 105 Pa
P2= 2.5 bar = ![]() Pa
Pa
Tubo:
D = 0.05 m
L = 8 m
e
/D = 0.01
Fig. 10 – Disegno dell’esercizio n° 1. L’autoclave.
Soluzione
Per risolvere questo esercizio ovviamente bisogna ricorrere all’equazione di Bernoulli
![]() (1)
(1)
considerando come sezioni 1 e 2 quelle indicate in figura.
La scelta di queste sezioni è giustificata dal fatto che le velocità dei peli liberi dell’acqua sono pressoché nulle ( W1 @ W2 @ 0 ); inoltre esse si trovano alla stessa quota (z2 – z1 = 0).
Considerando queste prime osservazioni possiamo semplificare la nostra equazione:
![]() (2)
(2)
Per calcolare le perdite di carico è necessario conoscere la velocità del fluido.
Quest’ultima la possiamo ricavare sapendo la portata in massa.
Infatti:
![]() (3)
(3)
Da cui si ottiene:
![]() (4)
(4)
Conosciamo la viscosità cinematica u
= m
/ r
= ![]() .
.
Possiamo quindi calcolare il numero di Reynolds:
![]() (5)
(5)
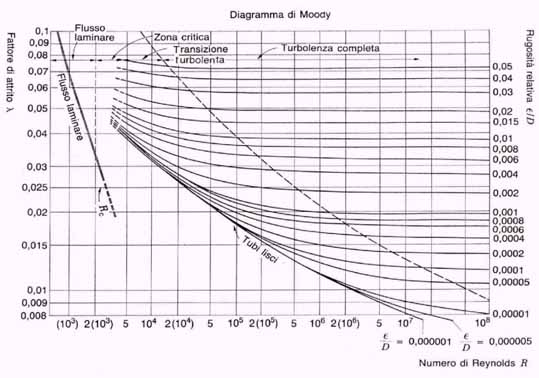
A questo punto conosciamo il numero di Reynolds e la scabrezza relativa e /D; possiamo quindi, consultando il diagramma di Moody, conoscere il valore del coefficiente d’attrito x = 0.0385.
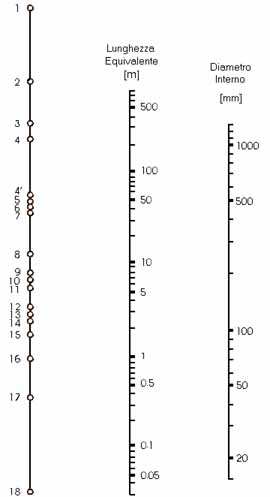
Le perdite di carico localizzate, sfruttando il Nomogramma, possono essere calcolate come perdite di carico distribuite su una determinabile lunghezza di tubo. Il nostro flusso di acqua incontra nell’ordine un imbocco e un allargamento brusco di sezione. Conoscendo il diametro interno del tubo (50 mm) e i numeri a cui corrispondono queste due accidentalità (14 e 17) è facile calcolare la lunghezza equivalente per ognuna delle due:
Imbocco: ![]()
Brusco allargamento: ![]()
Per una lunghezza equivalente totale di 2.7m.
Adesso abbiamo tutto i dati necessari per calcolare le perdite di carico totali:
![]() (6)
(6)
Riprendendo ora l’equazione di Bernoulli dalla quale siamo partiti possiamo calcolarci la prevalenza della pompa D p:
![]() (7)
(7)
Possiamo osservare che il valore delle perdite di carico è piuttosto piccolo. L’energia che la pompa fornisce al sistema non serve a vincere le perdite di carico che sono piccole grazie al fatto che il fluido usato (acqua) è poco vistoso e il tubo è corto ma viene immagazzinata come energia potenziale nell’autoclave.
Infine calcolo la potenza della pompa:
![]()
Testo
Una fontana è alimentata da una pompa di prevalenza D p. Determinare l’altezza h raggiunta dal getto.
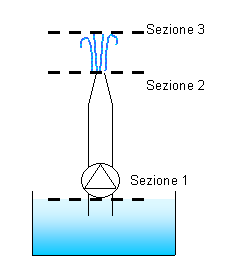
Dati
H = 2 m
D
p = 1 BAR = 105 Pa
D = 0.04 m
d = 0.01 m
e
= 0.05 mm
r
= 103 Kg/m3
u
= m
/r
= 10-6 m2/s
Fig. 11 – Disegno dell’esercizio n° 2. Fontana.
Soluzione
Per cominciare scegliamo 2 sezioni nella nostra fontana a cui faremo riferimento nella legge di Bernoulli. La prima sezione la scegliamo all’altezza del pelo dell’acqua nella fontana, mentre la seconda la scegliamo sull’orifizio in prossimità del restringimento in modo che il tubo avrà il diametro d.
Scriviamo l’equazione di Bernoulli:
![]() (1)
(1)
dove abbiamo tralasciato il termine ![]() in quanto le due sezioni scelte si trovano alla pressione atmosferica.
in quanto le due sezioni scelte si trovano alla pressione atmosferica.
Le incognite della nostra equazione sono 2 è quindi necessario introdurre un’ulteriore equazione per ottenere un sistema di due equazioni in due incognite.
Come seconda equazione, sfruttando l’equazione di continuità, prendiamo l’uguaglianza tra le portate nelle due sezioni:
![]() (2)
(2)
Da cui, considerando che S=p
D2, si ottiene: 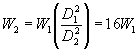
Dobbiamo quindi risolvere questo sistema:
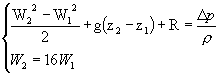 (3)
(3)
Facendo riferimento alla figura notiamo che z2 - z1 = H.
Calcoliamo ora le perdite di carico.
Utilizzando il Nomogramma come nell’esercizio precedente calcoliamo che la Leq dell’ugello vale 0.55 m; di conseguenza troviamo il valore delle perdite di carico in funzione del coefficiente d’attrito x :
![]() (4)
(4)
Sostituendo questa funzione nel nostro sistema otteniamo una seconda funzione W1=f(x
) di questo tipo: ![]() (5)
(5)
Come abbiamo visto nell’esercizio precedente il calcolo di x richiede la conoscenza del numero di Reynolds Re e della velocità che individueranno un determinato valore del coefficiente d’attrito sul diagramma di Moody. In questo caso non è però possibile calcolare Re in quanto esso stesso dipende dalla velocità W. La risoluzione di questo tipo di problemi richiede un procedimento iterativo. Per cominciare possiamo calcolare il valore di velocità che avremmo in presenza di un fattore di attrito nullo.
Quindi x = 0 à W1=0.794 m/s
Questo valore di velocità ci porterebbe a calcolare il seguente numero di Reynolds: ![]() (6)
(6)
Siamo in presenza di moto turbolento. Ora con quel determinato valore di Re e utilizzando la viscosità data e / D = 0.00125 leggiamo sul diagramma di Moody un nuovo valore di x diverso dal precedente che chiamiamo x *=0.027.
Con questo nuovo coefficiente d’attrito calcoliamo con la (5) una nuova velocità W1*=0.791 m/s. Questo nuovo valore, che differisce di pochissimo dal precedente (e di una quantità ancora minore dal successivo, provare per credere) posso considerarlo il mio valore definitivo.
Ritornando al sistema (3) calcolo infine la velocità sulla seconda sezione: W2 = 16 W1 = 12.64 m/s
Ora prendo in considerazione le sezioni 2 e 3. La formula di Bernoulli si riduce ad un’equazione estremamente semplice. L’altezza che il mio getto raggiunge quindi è: ![]()
Testo
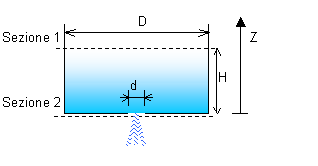
Un serbatoio di forma cilindrica ha un diametro di 1.06 m e contiene acqua sino ad un livello di 14 m. Sul fondo di esso viene aperto un foro circolare con bordi smussati (b = 0.5), con diametro pari ad 1/20 di quello del serbatoio, per cui l’acqua comincia ad uscire. Determinare il tempo t necessario al completo svuotamento del serbatoio.
Dati
D1 = 1.06 m
H = 10 = 14 m
D2 = (1/20)D1 = 0.053 m
b
= 0.5
Fig. 12 – Disegno dell’esercizio n° 3. Serbatoio.
Soluzione
Per cominciare occorre scegliere le due sezioni su cui operare. Ovviamente prenderemo come sezione 1 quella a pelo libero superiore mentre come sezione 2 quella in prossimità del foro sulla parte inferiore del serbatoio.
L’equazione generale di bilancio dell’energia di un sistema aperto è :
![]() (1)
(1)
Applicando questa equazione al nostro caso notiamo che le pressioni a cui si trovano le due sezioni sono le stesse (pressione atmosferica) e che l’altezza della prima sezione che si muove con il pelo dell’acqua varia nel tempo; dobbiamo quindi introdurre un’altezza variabile h.
Se consideriamo l’asse z delle altezze crescente dal basso verso l’alto abbiamo come posizione iniziale z1=h (generica posizione compresa tra H e 0) e come posizione finale z2=0. Di conseguenza la variazione di quota è z2 – z1 = -h
Infine l’unica perdita del nostro sistema è costituita dallo sbocco, quindi:
![]() (2)
(2)
Ricorrendo all’equazione di continuità
![]() (3)
(3)
posso trovare un’espressione che mi lega W2 a W1:
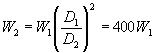 (4)
(4)
Sostituisco il valore ricavato nel bilancio energetico e ottengo : ![]() (5)
(5)
Raccolgo a fattore comune la velocità :
![]() (6)
(6)
La velocità può essere espressa come derivata della variazione di altezza nel tempo :
![]() (7)
(7)
Il segno meno è necessario in quanto indica che la variazione di altezza è contraria all’asse di riferimento z .
Eguagliando le due equazioni si ottiene:
![]() (8)
(8)
Questa è un’equazione differenziale di 1° grado a variabili separabili. Integrando:
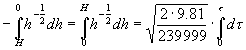 (9)
(9)
Poiché la risoluzione generale dell’ integrale al primo membro è :
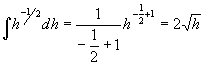 (10)
(10)
Otteniamo :
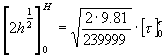 (15)
(15)
![]() (16)
(16)
Sostituendo i valori numerici troviamo la soluzione al problema :
![]() (17)
(17)
APPENDICE
|
materiale |
e (mm) |
|
acciaio chiodato |
0.0 – 9.0 |
|
cemento |
0.3 – 3.0 |
|
doghe in legno |
0.19 – 0.9 |
|
fusione in ferro |
0.25 |
|
ferro zincato |
0.15 |
|
ferro asfaltato |
0.12 |
|
acciaio commerciale |
0.046 |