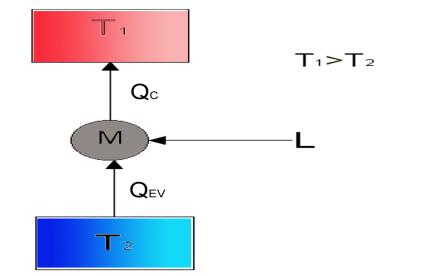
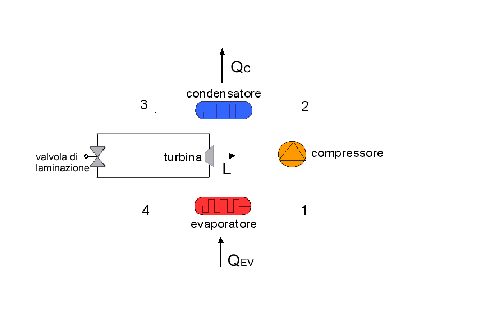
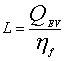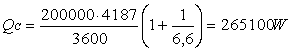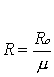In questo caso si ha :

- il condensatore in cui il vapore corre nel tubo a serpentina mentre all’ esterno vi è l’aria fredda;

- l’evaporatore che ha funzione della caldaia nel ciclo Rankine;

- il compressore che compie una trasformazione adiabatica reversibile (isoentropica)

- la turbina oppure la valvola di laminazione (che dà luogo ad una trasformazione irreversibile).

Il fluido utilizzato è nel 70% dei casi l’ammoniaca e per il restante 30% il Freon (miscela di CloroFluoroCarburi). I pregi dell’ammoniaca sono il costo irrisorio e le migliori proprietà termodinamiche (il diagramma è noto) ma purtroppo è tossica. Il Freon è stato brevettato per la prima volta dalla Dupont ; esistono un numero considerevole di queste miscele ed ognuna ha un diagramma termodinamico diverso quindi la maggiore fonte di informazioni in merito rimane il produttore. Il più noto è il Freon 12 (I generazione, il brevetto dura 20 anni) ma anch’esso è tossico in quanto danneggia lo strato di ozono. Negli anni sono state sviluppate miscele di II e III generazione.

Analizziamo il funzionamento della macchina considerando il diagramma p-v

prendendo in considerazione le due differenti ipotesi (la turbina oppure la valvola di laminazione) :

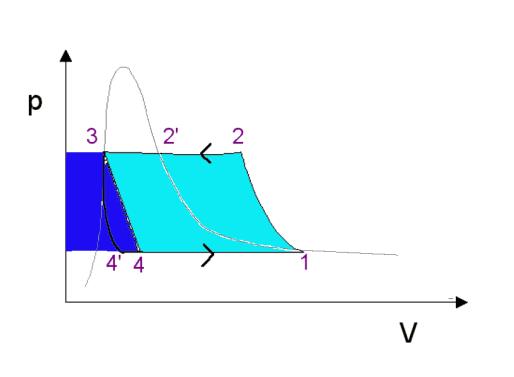
Fig. 3

1-2 Il fluido, che in 1 si trova allo stato di vapore saturo secco (titolo unitario), passa attraverso un compressore che ne aumenta la pressione per mezzo di una trasformazione adiabatica reversibile. Durante questo passaggio si verifica un aumento significativo della temperatura del fluido, che in 2 si trova nel campo del vapore surriscaldato.

2-2’, 2’-3 Il fluido percorre la serpentina del condensatore e cedendo calore QC comincia a raffreddarsi (2-2’) a pressione costante, fino a raggiungere in 2’ lo stato di vapore saturo secco; a questo punto, sempre a pressione costante, il vapore comincia a condensare (2’-3) e a temperatura costante giunge in 3, che si trova sulla curva limite inferiore (titolo 0).

3-4 Il fluido entra nella valvola di laminazione e subisce una trasformazione isoentalpica (h3 = h4) che ne diminuisce la pressione e la temperatura e ne aumenta il volume. L’uso della valvola fa sì che questa trasformazione non sia più adiabatica reversibile come nel caso della turbina (3-4’), anzi, la valvola rende questo processo fortemente irreversibile e da ciò deriva l’impossibilità di tracciare un percorso definito da 3 a 4. Altrettanto indefinita risulta essere l’area del ciclo frigorifero, e questo rappresenta uno svantaggio rilevante.

4-1 Il fluido, che in 4 è quasi completamente liquido, entra nell’evaporatore e a pressione costante comincia la vaporizzazione assorbendo il calore QEV fornito al sistema , fino a raggiungere lo stato iniziale 1 nel quale può ricominciare il ciclo.

La serpentina del condensatore dev’essere il più libera possibile per cedere facilmente calore. Viceversa sarà necessario un aumento di temperatura che comporterà evidentemente un aumento di consumi. La differenza di temperatura tra evaporatore e condensatore è dell’ordine di 30 – 35 °C a cui corrisponde una variazione di pressione di 4 – 5 bar. Quindi per minimizzare il lavoro è necessario diminuire il DT.

Con la turbina si recupera una quota di lavoro ma questo organo è complesso e costoso (anche se di piccole dimensioni). Questo non è possibile con la valvola che è più economica ma noteremo più avanti che il lavoro recuperato sarebbe praticamente trascurabile

Analizziamo per comodità il diagramma T-s

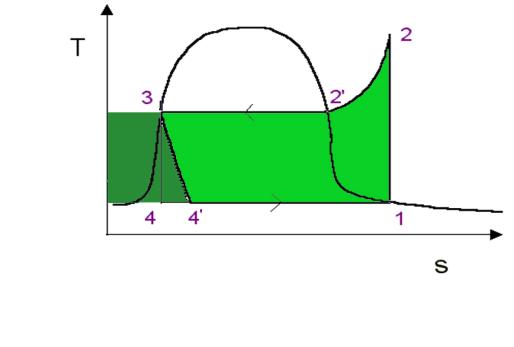
Fig. 4

L’area sottesa è priva di significato essendo appunto il ciclo irreversibile.

La valvola è collocata tra la serpentina del condensatore e la cella frigorifera, ha la forma di un capillare in modo che il fluido perda pressione nello strozzamento: se non si mantiene DP non si mantiene DT. Esiste un punto ottimo di chiusura della valvola che produce la massima performance della macchina.

Con il diagramma h-s osserviamo che:

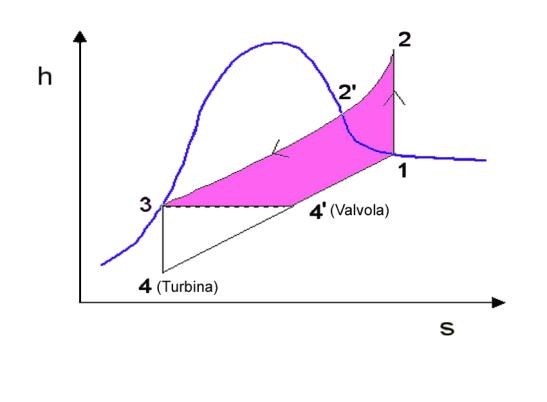
Fig. 5

con la valvola la trasformazione è isoentalpica e irreversibile perché Q=0, L=0 allora h3 = h4 mentre con la turbina è isoentropica e reversibile.

Il diagramma più usato è il p-h

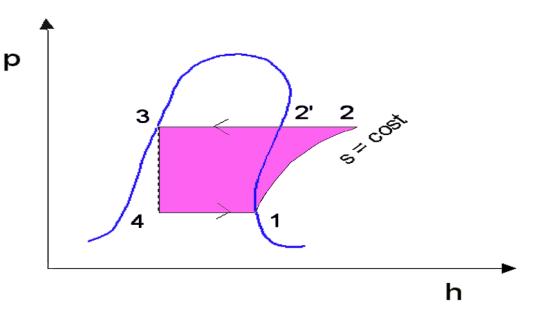
Fig. 6

Esso è riferito al Freon 12. Non essendo disponibili tabelle la soluzione grafica è l’unica fonte di informazioni nella risoluzione dei problemi pratici.

Per il calcolo delle prestazioni termodinamiche della macchina si possono utilizzare due grandezze distinte:

- l’effetto utile frigorifero (se si vuole raffreddare il serbatoio a temperatura minore)

definito come

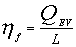
dove QEV è il calore assorbito e L il lavoro richiesto dal sistema.

Di solito il coefficiente hf vale 5 – 6.

- il coefficiente di prestazione (se si usa la macchina come pompa di calore)

definito come

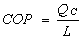
dove QC è il calore fornito e L il lavoro richiesto dal sistema.

Vale inoltre la seguente relazione

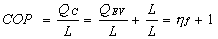
cioè si dimostra che il funzionamento come pompa di calore è più conveniente rispetto a quello come macchina frigorifera.

ESEMPIO.

Una macchina frigorifera utilizza come refrigerante il Freon F12, che fornisce il calore QEV=200000 frigorie/h. Conoscendo le due temperature Tev=5°C e Tcond=40°C, considerando la compressione isoentropica (s2=s1) e l’espansione isoentalpica (h4=h3), determinare il coefficiente di effetto utile frigorifero, il coefficiente di prestazione, il calore prodotto QC, il lavoro assorbito L .

Qui sotto sono rappresentati i dati del problema e il diagramma p-h:

Trasformazione	Pressione (BAR)	Temperatura (°C)	Entalpia specifica (KJ/Kg)
1	3,6	5	353,6
2	9,6	50	371,1
3	9,6	40	238,5
4	3,6	5	238,5

Innanzi tutto occorre ricordare che la grandezza L indica un rapporto fra energia e tempo, quindi ci viene richiesta la potenza meccanica assorbita dalla macchina, così come QC rappresenta la potenza termica erogata.

Calcoliamo il coefficiente di effetto utile frigorifero:

Per capire bene il valore di questo risultato dobbiamo confrontarlo con il coefficiente di una macchina frigorifera basata sul ciclo di Carnot inverso, per la quale il coefficiente risulta massimo. In questo caso scegliamo come temperature t1 e t2 i due valori 40°C e 5°C, per cui il coefficiente risulterà :

Confrontando i due valori notiamo che non c’è una grande differenza, quindi possiamo concludere che l’effetto utile frigorifero della nostra macchina è elevato .

Calcoliamo ora il COP :

COP = 6,6 + 1 = 7,6

Sapendo poi che e che otteniamo una relazione che più genericamente può essere scritta così :

Se adesso convertiamo le unità di misura otteniamo che: 200000 frig/h = 200000 Kcal/h, 1Kcal = 4187 J, 1 h = 3600 s , così sostituendo abbiamo :

L = 34920W

MISCELE DI ARIA E VAPORE ACQUEO

L’aria sarà considerata come un solo componente e la sua composizione sarà assunta costante. La composizione di dettaglio in volume dell’aria secca è:

78% Azoto

21% Ossigeno

1% Gas rari (tra cui elio, neon, argon) e una piccolissima percentuale di Anidride Carbonica. All’aria aperta la percentuale di CO₂ è circa 0.03%, quindi si può considerare quasi assente.

L’acqua potrà essere in parte liquida ed in parete vapore.

La fase gassosa della miscela sarà considerata una miscela di due gas ideali: aria e vapore acqueo infatti il vapore presenta una pressione parziale molto piccola, quindi è lecito trascurare il comportamento da vapore surriscaldato. La composizione

della fase gassosa potrà variare, per effetto di evaporazione o condensazione di acqua.

Quindi la massa di aria secca viene considerata costante (perché l’aria non si crea ne si distrugge a parte casi rari) mentre la massa di vapore cambia facilmente. Questo fatto spiega perché le grandezze specifiche non vengono riferite all’unità di massa della miscela, ma all’unità di massa dell’aria secca (si mantiene questa convenzione anche per compatibilità con il passato e per comodità). Ad esempio si parla di entalpia specifica definita come:

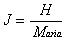ove M_aria= massa dell’aria secca.

Saturazione dell’aria e titolo

Consideriamo il seguente esperimento: in presenza di aria inizialmente secca poniamo su una bilancia un recipiente contenente acqua mantenendo pressione P e temperatura T costanti.

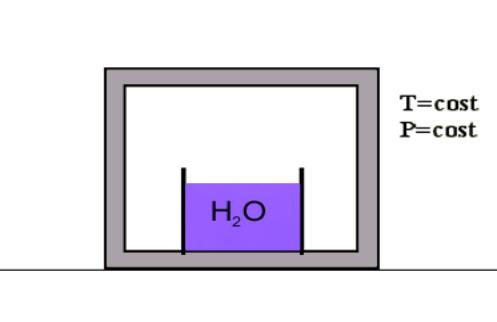
Fig. 7

Dopo un certo periodo di tempo il livello di acqua nel contenitore sarà calato, cioè una certa massa di H₂O sarà evaporata nell’aria , e il livello continuerà a calare sempre più lentamente fino a rimanere costante (quindi la bilancia misurerà una diminuzione della massa di acqua)

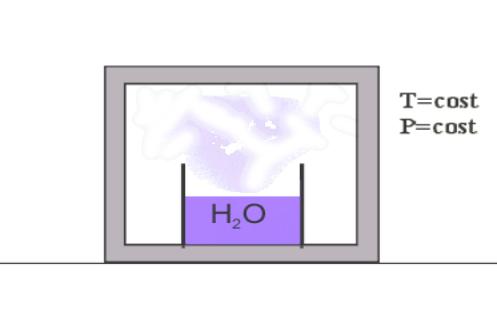
Fig. 8

Questa esperienza mostra che se si mettono a contatto aria e acqua liquida , a temperatura e pressione costanti , l’acqua evapora fino a che la pressione parziale del vapore saturo eguaglia la pressione di saturazione dell’acqua alla temperatura T alla quale si opera.

In altri termini la presenza d’acqua non influisce sulla quantità di acqua che si volatilizza , ma soltanto sulla velocità del processo.

A questo punto possiamo introdurre una nuova grandezza : il titolo, definito come

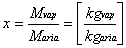( 1 )

ove M_vap= massa di acqua evaporata

M_aria= massa di aria secca

Kg_vap = chilogrammi di vapore

Kg_aria = chilogrammi di aria

Il titolo è il rapporto tra pesi di sostanze chimiche diverse e non si tratta quindi di un numero puro. Non va confuso con il titolo di vapore saturo che invece è un numero puro. Inoltre il titolo x non è confinato ad essere minore di 1 (ricordiamo che per il titolo di vapore saturo vale x_{vapore saturo} < 1).

Di solito per evitare semplificazioni dell’unità di misura, il titolo viene espresso in g_vap/kg_aria.

La grandezza che esprime quale è la massima massa di acqua che può volatilizzarsi in una massa di aria secca è il titolo di saturazione, cioè il titolo calcolato in condizioni di equilibrio tra aria e acqua in presenza di acqua liquida (in riferimento all’esperimento visto, il titolo calcolato quando il livello dell’acqua resta costante).

Il titolo di saturazione x_sat è dipendente da temperatura e pressione

x_sat= x_sat (p,t), ad esempio cresce al crescere della temperatura, quindi quando si parla di titolo di saturazione si considerano fissati i valori di questa due grandezze.

Solitamente si lavora in un sistema isobaro , a pressione atmosferica p_atm=1,013 bar quindi la dipendenza viene ad essere dalla sola temperatura.

I valori del titolo di saturazione riferiti alla pressione atmosferica in funzione della temperatura sono reperibili su apposite tabelle.

Tabella 1

Tabella dei valori assunti da alcuni parametri termodinamici della miscela aria-vapore acqueo per j = 1 e P = 1.013 bar

Temperatura dell’aria T °C	Pressione di vapore dell’aria satura P mbar P mmHg		Titolo di saturazione x g/Kg
-20	1.02	0.756	0.63
-19	1.13	0.848	0.7
-18	1.25	0.938	0.77
-17	1.37	1.028	0.85
-16	1.5	1.125	0.93
-15	1.65	1.238	1.01
-14	1.81	1.358	1.11
-13	1.98	1.485	1.22
-12	2.17	1.628	1.34
-11	2.37	1.778	1.46
-10	2.59	1.943	1.6
-9	2.83	2.123	1.75
-8	3.09	2.318	1.91
-7	3.36	2.520	2.08
-6	3.67	2.753	2.27
-5	4	3	2.49
-4	4.36	3.270	2.69
-3	4.75	3.563	2.94
-2	5.16	3.870	3.19
-1	5.61	4.208	3.47
0	6.09	4.568	3.78
1	6.56	4.920	4.07
2	7.04	5.280	4.37
3	7.57	5.678	4.7
4	8.11	6.083	5.03
5	8.7	6.526	5.4
6	9.32	6.991	5.79
7	9.99	7.493	6.21
8	10.7	8.026	6.65
9	11.46	8.596	7.13
10	12.25	9.188	7.63
11	13.09	9.818	8.15
12	13.99	10.493	8.75
13	14.94	11.206	9.35
14	15.95	11.963	9.97
15	17.01	12.759	10.6
16	18.13	13.599	11.4
17	19.32	14.491	12.2
18	20.59	15.444	12.9
19	21.92	16.441	13.8
20	23.31	17.484	14.7
21	24.8	18.602	15.6
22	26.37	19.779	16.6
23	28.02	21.017	17.7
24	29.77	22.3	18.8
25	31.6	23.702	20
26	33.53	25.150	21.4
27	35.56	26.672	22.6
28	37.71	28.285	24
29	39.95	29.965	25.6
30	42.32	31.748	27.2
31	44.82	33.618	28.8
32	47.46	35.575	30.6
33	50.18	37.638	32.5
34	53.07	39.806	34.4
35	56.1	42.078	36.6
36	59.26	44.449	38.8
37	62.6	46.954	41.1
38	66.09	49.572	43.5
39	69.75	51.317	46
40	73.58	55.198	48.8
41	77.59	58.197	51.7
42	81.8	61.355	54.8
43	86.18	64.64	58
44	90.79	68.098	61.3
45	95.6	71.706	65
46	100.61	75.464	68.9
47	105.87	79.409	72.8
48	111.33	83.504	77
49	117.07	87.81	81.5
50	123.04	92.288	86.2
55	150.94	117.715	114
60	198.7	149.037	152
65	249.38	187.05	204
70	310.82	233.134	276
75	384.5	288.398	382
80	472.28	354.239	545
85	576.69	432.553	828
90	699.31	524.525	1400
95	834.09	625.618	3120
100	1013	759.812	-

Il titolo di saturazione non dipende dalla presenza dell’aria , ma esclusivamente dal vapore. Nell’esperimento precedentemente visto la massa di acqua evaporata sarebbe stata la medesima anche in assenza di aria (nel vuoto) in quanto , per ipotesi di gas perfetto, il vapore si espande come se l’aria non ci fosse.

L’unica differenza è data dalla velocità di vaporizzazione in quanto la presenza dell’aria rallenta il raggiungimento dell’equilibrio.

Il concetto che sia l’aria a saturarsi è sbagliato perchè in realtà è l’acqua che si satura.

Grado igrometrico

Il titolo x è un numero piccolo e preso a se stante non ci da una indicazione diretta del livello di saturazione del vapore acqueo nella miscela : per capire se l’aria sia secca o satura è necessario confrontare il titolo con quello di saturazione . Quindi si rende opportuno introdurre una nuova grandezza: il grado igrometrico , definito come :

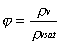( 2 )

ove r_v= massa del vapore acqueo contenuto nell’unità di volume della fase gassosa

r_vsat= masa del vapore acqueo che sarebbe contenuto nell’unità di volume della fase gassosa in condizioni di saturazione (cioè in equilibrio con in liquido)

Poichè per un gas ideale , a temperatura fissata , la densità è proporzionale alla pressione si ha anche , equivalentemente:

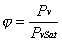( 3 )

ove P_v = pressione parziale di vapore acqueo nella miscela

P_{v Sat} = pressione di vapore saturo secco

(fissata la temperatura T della miscela)

Il grado igrometrico può assumere valori compresi tra 0 e 1 , oppure in modo equivalente può essere espresso in percentuale ; in tal caso prende il nome di umidità relativa .

Per capire meglio cosa sia in pratica il grado igrometrico affidiamoci a questo esempio:

Consideriamo una massa d’aria umida alla temperatura T = 20°C. La pressione di saturazione ad una tale temperatura è P_sat = 23.31 mbar (questo valore è stato ricavato dalla Tabella 1) e la pressione parziale del vapore contenuto nella miscela è P_v = 16.317 mbar.

Il grado igrometrico si ricava dalla ( 3 ) sostituendo i valori numerici forniti:

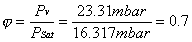(o equivalentemente Umidità relativa = 70%)

Questo significa che la miscela contiene il 70% della quantità di vapore che la renderebbe satura.

Quindi il grado igrometrico j ci da una misura immediata di quanto l’aria sia effettivamente prossima alla saturazione.

Ricaviamo allora la relazione tra titolo e grado igrometrico

Consideriamo una miscela di aria e vapore acqueo , in assenza di liquido. Noto il grado igrometrico j vogliamo ricavare il titolo x relativo alla miscela.

Per le ipotesi precedentemente fatte , è lecito considerare aria e vapore acqueo0 come due gas ideali. Quindi possiamo scrivere l’equazione di stato dei gas perfetti separatamente per la massa d’aria e la massa di vapore acqueo, considerando come volume a disposizione delle singole massa il volume totale. (questa assunzione discende dalla Legge di Dalton sulle miscele dei gas perfetti)

Quindi

Aria 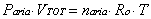( 4 )

Vapore acqueo 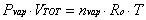( 5 )

Essendo valide le seguenti relazioni

( 6 ) ( 6 )

( 7 ) ( 7 )

ove n = numero di moli del gas

M = massa del gas

n = numero di moli del gas

m =massa molare del gas n = numero di moli del gasn = numero di moli del gas m = massa molare del gas n = numero di moli del gas m = massa molare del gas

m = massa molare del gas

si ottiene:

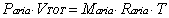Aria ( 8 )

Vapore acqueo 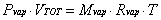( 9 )

Dividendo membro a membro la ( 8 ) e la ( 9 ) otteniamo:

allora (10) ( 10 )

Ricordiamo che per definizione di titolo

( 1 )

Quindi per la ( 6 ) e la ( 10 ) si ha :

( 11 )

I valori delle masse molari di aria e vapore d’acqua sono rispettivamente :

m = 29 kg/mol e m = 18 kg/mol.

Sostituendoli nella ( 11 ) arriviamo alla

( 12 )

Questa relazione ci permette di calcolare il titolo a partire dalle pressioni parziali di vapore e aria secca.

Dalla definizione di grado igrometrico ( 3 ) si ricava:

( 13 )

Sostituendo la (13 ) nella ( 12 ) si ottiene:

( 14 )

Dovendo inoltre valere che

( 15 )

ove P_TOT = pressione totale della miscela (di solito nota e pari a 1 bar)

Si arriva alla formula che esprime la relazione cercata tra titolo x e grado igrometrico j:

( 16 )

Entalpia specifica

L’entalpia è una proprietà estensiva. Pertanto ,l’entalpia specifica j .cioè l’entalpia per chilogrammo di aria , sarà data dalla somma dell’entalpia di 1 Kg di aria e l’entalpia di X Kg di aria , dove X è il titolo della miscela ovvero il contenuto di vapore nell’aria.

Se siamo in assenza di acqua liquida ,sia l’aria sia l’acqua possono essere considerati gas ideali. Si adottano usualmente le seguenti convenzioni:

Per l’aria:

nelle condizioni di gas ideale, alla temperatura T=0° C entalpia specifica h= 0

Per l’acqua:

alla temperatura T=0 °C entalpia specifica h=0 per il liquido sulla curva limite inferiore. (Ricordiamo che in realtà la temperatura minima sulla curva limite inferiore è quella del punto triplo , ma spesso si approssima la temperatura del punto triplo dell’acqua con il valore 0 °C).

Con queste convenzioni si ha :

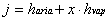( 20 )

Cerchiamo una espressione della ( 20 ) con i valori numerici esplicitati.

Scriviamo l’equazione che descrive l’entalpia del vapore acqueo nel punto C:

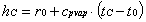( 21 )

Sapendo che :

1. la temperatura del punto A è quella del punto triplo T_A=T₀= 0 °C

2. r₀_»2500 KJ/Kg dove r₀ ,calore latente di vaporizzazione dell’acqua a 0 °C, può essere ricavato dalle tabelle delle proprietà termodinamiche dell’acqua e del vapore saturo e corrisponde alla variazione di entalpia tra i punti A e B .

3. il calore specifico del vapore acqueo può essere assunto circa costante per temperature basse come quella ambiente : c_pvap» 1,9 KJ/Kg.

Si ottiene:

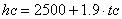( 22 )

dove t_C è al temperatura espressa in gradi Celsius.

Dalla espressione dell’entalpia per i gas perfetti si ottiene:

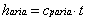( 23 )

ed essendo il calore specifico dell’aria c_paria=1 KJ/Kg

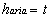( 24 )

Quindi sostituendo i valori ottenuti nella ( 20 ) si ricava:

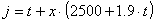( 25 )

Notiamo che la ( 25 ) è una formula dimensionalmente non omogenea , una formulazione più corretta ( che ha un significato fisico ) sarebbe :

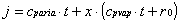( 26 )

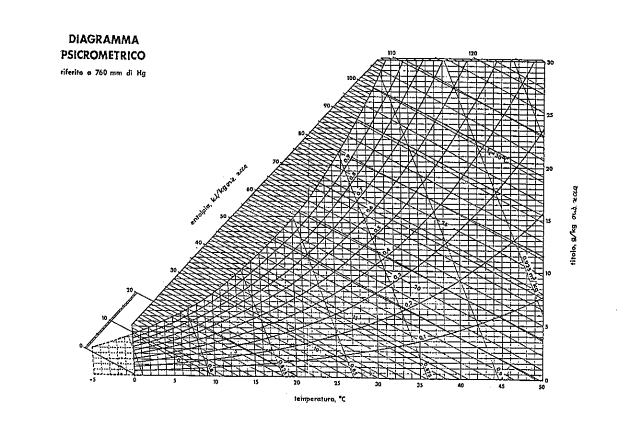
Diagramma Psicrometrico

Sul diagramma psicrometrico è possibile individuare gli stati di equilibrio delle miscele d’aria e acqua (che possono interessare anche il dimensionamento di condizionatori e impianti per il trattamento dell’aria).

Su tale diagramma sono indicati tre assi:

1. Asse x, verticale, posto nel margine destro, sul quale si possono leggere i valori del titolo della miscela in g_vap/Kg_aria;

2. Asse T, orizzontale, sul quale si possono leggere le temperature espresse in °C.

3. Asse j posto diagonalmente nel margine sinistro, sul quale si possono leggere i valori dell’entalpia specifica in kJ/Kg_ariasecca.

Forniamo un esempio di diagramma psicrometrico ad una pressione pari a 1.013 Bar.

CICLI FRIGORIFERI