APPLICAZIONI SULLE PERDITE DI CARICO
Analogie fra circuiti idraulici e circuiti
elettrici
Dal modo in cui è stata introdotta, R può
essere vista come una specie di “resistenza idraulica”, in analogia con la
resistenza elettrica. In effetti R comprende tutti gli elementi che
tendono a frenare il flusso del fluido attraverso le condutture, comportamento molto simile a quello della
resistenza elettrica nei confronti delle correnti.
In R è infatti raccolta la somma di tutte le resistenze distribuite dovute alla viscosità del fluido e di tutte le resistenze concentrate dovute a curve, filtri, pompe e ostacoli vari presenti nelle condutture.
Oltre alla resistenza è possibile osservare che
esistono molte altre analogie con l’elettrotecnica che permettono di immaginare
il “circuito idraulico” come un circuito elettrico.
|
IDRAULICA |
ELETTROTECNICA |
|
Pressione p |
Potenziale V |
|
Perdita di carico D p |
Differenza di potenziale D V |
|
Portata
in massa |
Corrente I |
|
Effetti dissipativi R |
Resistenza R |
|
Pompa |
Generatore |
|
Serbatoio |
Condensatore |
|
Inerzia del fluido |
Induttanza |
Tab.1 – analogie tra idraulica ed elettrotecnica
Come si può osservare dalla tabella 1 è possibile
paragonare ogni componente “idraulico” ad un equivalente elettrotecnico, sempre
paragonando lo scorrere del fluido al flusso di corrente.
Ovviamente il paragone appena proposto non è
assoluto, esistono infatti sostanziali differenze fra i due sistemi, la più
importante riguardante proprio la resistenza. Nell’elettrotecnica infatti la
relazione che lega differenza di potenziale e corrente è la legge di Ohm
che è una relazione lineare, infatti:
![]() (1)
(1)
Nell’idraulica invece l’equazione corrispondente è
più complessa in quanto non più lineare. La perdita di carico è infatti
linearmente dipendente dal quadrato della velocità del fluido e quindi dal
quadrato della portata in massa.
![]() (2)
(2)
Un ruolo fondamentale nei circuiti idraulici viene
svolto dalle pompe, come nei circuiti elettrici viene svolto dai generatori.
Infatti compito delle pompe è fornire l’energia necessaria per garantire lo
scorrere del fluido bilanciando le perdite distribuite e concentrate che si
hanno lungo il circuito.
Se nella figura 1 confrontiamo le caratteristiche
di una pompa e di un generatore elettrico notiamo una grande somiglianza,
addirittura possiamo paragonare il flusso massimo alla corrente di corto
circuito del generatore.

Figura 1 - Caratteristiche di una pompa e di un generatore
Nelle pompe centrifughe posso però avere più
caratteristiche a seconda del numero di giri della pompa (figura 2), cosa non
possibile in un generatore elettrico.
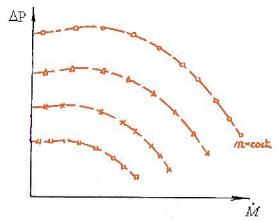
Figura 2 - Caratteristica di una pompa centrifuga
Se ora confronto la caratteristica di una pompa
centrifuga con il grafico che riporta
la relazione fra prevalenza e flusso (figura 3), noto che dalla sovrapposizione
delle due posso stabilire una sorta di “punto di funzionamento” per le pompe
idrauliche (figura 4).
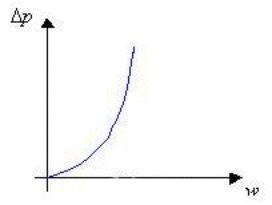
Figura 3 - Relazione fra prevalenza e flusso
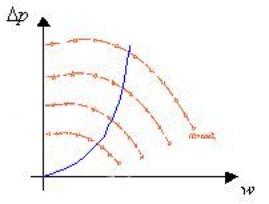
Figura 4 - Punto di funzionamento
Dobbiamo quindi fissare la portata del circuito e
quindi, riportandola sulla relazione DPµM2 ,
trovare la prevalenza minima che deve fornire la pompa per garantire lo
scorrere del fluido nel circuito (figura 5).

Figura 5 - Identificazione della prevalenza minima
Una volta identificata la prevalenza minima si può
agire sulla pompa fissando il numero di giri ideale per il corretto scorrere
del fluido lungo le tubature. Se il numero di giri fissato fosse troppo elevato
potrebbe avere luogo la cavitazione, fenomeno che crea turbolenze e bolle
d’aria che possono portare alla rottura delle palette della turbina.
Se la prevalenza fissata è uguale o di poco
superiore alla prevalenza minima si dice che “la pompa copre le perdite”.
Ovviamente esiste anche un parametro che tiene
conto del rendimento meccanico della pompa e questi è h, definito come:
![]() (3)
(3)
Per cui h è il rapporto fra la potenza trasmessa al fluido
e la potenza assorbita dal motore della pompa.
Ricordiamo che:
![]() (4) (3)
(4) (3)
Si potranno identificare nella caratteristica
curve ad uguale rendimento (figura 6).
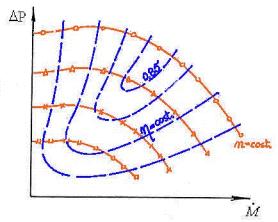
Figura 6 - Curve ad uguale rendimento
Ovviamente sarà più conveniente dal punto di vista
del risparmio energetico e quindi economico impostare un funzionamento a
rendimento elevato. Lavorando inoltre al corretto regime si possono anche
ridurre la rumorosità della pompa e limitare l’eccessiva usura elle palette.
Tipicamente per le pompe a centrifuga i rendimenti
sono compresi fra 0.7 e 0.8.
Alla luce delle considerazioni effettuate il
grafico che dovremo riscontrare è quello di figura 7.

Figura 7 - Grafico richiesto
Le tre curve sono quella della relazione
portata-cadute del circuito, quella di funzionamento della pompa e quella del
rendimento nei confronti della portata.
Si può osservare che la prevalenza bilancia le
perdite del circuito esattamente nella zona di massimo rendimento, venendo
incontro alle nostre aspettative.
L’area tratteggiata è la potenza trasmessa al
fluido nella condizione di funzionamento a meno dell’inverso della densità r.
ESERCIZI
Per risolvere gli esercizi di idraulica è
solitamente necessario applicare l’equazione di bilancio dell’energia, che
nell’idraulica è
![]() (5)
(5)
A seconda del tipo di esercizio possiamo avere la
presenza di tutti i termini della relazione o solo parte di essi.
Ad esempio in presenza di un circuito posto
interamente alla medesima altezza
possiamo porre
![]() (6)
(6)
e quindi
![]() (7)
(7)
Inoltre è possibile porre
![]() (8)
(8)
e quindi
![]() (9)
(9)
Per cui la relazione (5) diventa
![]() (10)
(10)
Esistono infiniti casi analoghi a quello
illustrato in cui uno o più parametri della relazione (5) si annullano, per cui
in generale basta porre attenzione nella scelta dei circuiti e dei riferimenti
per limitare i calcoli riducendo sia il tempo di risoluzione che il pericolo di
commettere errori.
Esercizio 1
Consideriamo un impianto che trasferisce olio da un serbatoio dato a uno a quota superiore:
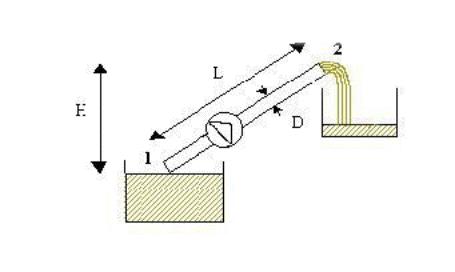
Figura 8 - Disegno esercizio 1
I
dati del problema: 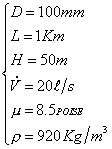
Si chiede di calcolare il fattore di attrito x , la caduta di pressione nel condotto, la prevalenza della pompa e la sua potenza, la variazione di temperatura dell’olio.
Se poniamo come sezione 1 e 2 rispettivamente l’entrata e l’uscita della conduttura (riferendo ovviamente i termini "entrata" e "uscita" al moto del fluido) possiamo affermare che:
![]() (11)
(11)
e considerare:
![]() (12)
(12)
Infatti la velocità in entrata è ritenuta nulla perché il liquido contenuto nel serbatoio 1 può essere ritenuto stabile con buona approssimazione; le pressioni in entrata e in uscita sono la differenza di pressione atmosferica fra le due altezze e possono essere considerate uguali perché la differenza è irrilevante rispetto ai valori che saranno in gioco nel nostro circuito.
Infatti quantificandole:
![]() (13)
(13)
Calcoliamo il fattore di attrito (con A indicheremo la sezione della conduttura).
![]() (14)
(14)
![]() (15)
(15)
Il moto è dunque laminare poiché il numero di Reynolds è minore di 2100: non abbiamo perciò bisogno del diagramma di Moody per determinare x:
![]() (16)
(16)
Calcoliamo ora la perdita di pressione dovuta alla viscosità dell’olio:
![]() (17)
(17)
E’ quindi evidente che la differenza di pressione tra le sezioni di ingresso e uscita è trascurabile rispetto alle altre perdite di pressione; siamo di fronte a pressioni abbastanza alte: tale fenomeno richiederà una scelta molto competente della pompa per evitare problemi che potrebbero rivelarsi molto pericolosi per l’ incolumità del personale oltre che antieconomici.
Dobbiamo osservare a questo punto che le perdite distribuite dovute alla viscosità dell’olio sono le uniche perdite presenti in quanto abbiamo supposto la totale assenza di moduli che potrebbero disturbare il normale scorrere del fluido e quindi la totale assenza di perdite concentrate.
La prevalenza necessaria a compensare le perdite sarà:
![]() (18)
(18)
Quindi:
![]() (19)
(19)
I tre termini componenti la relazione appena espressa sono rispettivamente dati da dalle perdite di pressione distribuite lungo il tubo, dalla differenza di altezza fra i serbatoi di ingresso e uscita e dalla differenza di velocità del fluido alle estremità del condotto.
Da qui siamo ora in grado di stabilire quale dovrà essere la reale potenza della pompa mediante l’ applicazione della relazione:
![]() (20)
(20)
Un’analisi dei dati fino ad ora calcolati rende immediatamente che le perdite dovute alla viscosità del fluido sono la causa principale dell’elevata potenza richiesta alla pompa.
Passiamo ora infine a ricavarci la variazione di temperatura dell’olio lungo il percorso che possiamo aspettarci dell’ordine di qualche grado, soprattutto se vediamo che il fluido considerato ha una notevole viscosità, fattore questo che indirettamente condiziona la variazione di temperatura in quanto fa aumentare la potenza della pompa.
![]() (21)
(21)
La relazione espressa sopra è valida solo se, come nel nostro caso, si suppone il tubo isolato termicamente dall’esterno e quindi si può trascurare il termine relativo al calore. Ovviamente nella realtà è impossibile ottenere una tale condizione poiché non è fisicamente realizzabile un isolamento perfetto e in più sarebbe del tutto antieconomico realizzare un buon impianto isolante per un condotto della lunghezza supposta impiantato in un ambiente esposto alle intemperie.
Possiamo sfruttare la relazione:
![]() (22)
(22)
Uguagliando le relazioni (20) e (21) possiamo ricavare la differenza di temperatura del fluido dopo il passaggio dal condotto che quindi risulta:
![]() (23)
(23)
La variazione di temperatura trovata non è
trascurabile per cui si renderà
necessario studiare l’impiego di dispersori di calore come radiatori per
ovviare a possibili problemi derivanti dal surriscaldamento dell’impianto.
Esercizio 2
Dobbiamo progettare un impianto di irrigazione per un campo di 200 ettari:
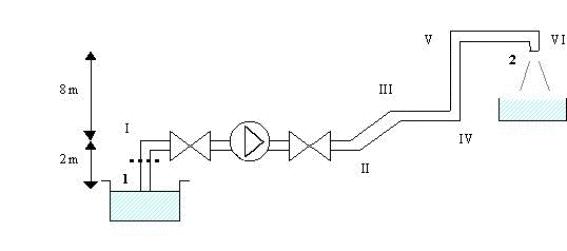
Figura 9 - Disegno esercizio 2
Altri
dati del problema: 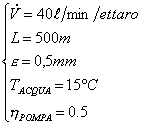
Il problema chiede di calcolare il diametro della conduttura e la prevalenza e la potenza della pompa: occorrerà perciò ricavarsi il diametro ideale per il tipo di impiego proposto fra i tubi UNI perché è impensabile farsi costruire a livello industriale dei tubi del diametro desiderato in quanto oltre che una notevole perdita di tempo per l’acquirente e per il costruttore, una simile operazione comporterebbe anche dei costi elevatissimi, molto probabilmente sproporzionati rispetto al costo totale dell’opera idraulica da eseguire.
Proviamo ora quindi a porre un “diametro di primo tentativo”, cioè a porre un diametro di prova per poter poi correggere più opportunamente i dati in seguito.
Scegliere un diametro “a occhio” non è però una cosa molto ragionevole. Conviene invece conoscendo la portata fare riferimento a una velocità media dell’acqua di 3m/s che l’esperienza suggerisce essere un buon valore.
Possiamo ora quindi ricavarci il diametro del tubo richiesto:
![]() (24)
(24)
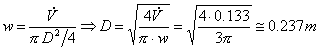 (25)
(25)
Se ora consultiamole tavole UNI per i diametri nominali delle condutture idrauliche possiamo identificare i due valori che più si avvicinano al diametro cercato sono 244.5mm e 273mm a cui corrispondono i diametri interni di 232mm e 260.4mm. A questo punto è più opportuno scegliere il diametro minore per motivi di leggerezza, praticità ed economicità anche se una tale scelta comporterà l’ uso di una pompa dotata di maggior potenza per poter sopperire alla portata richiesta.
|
Diametro esterno (mm) |
Spessore normale (mm) |
Massa (kg/m) |
Diametro esterno (mm) |
Spessore normale (mm) |
Massa (kg/m) |
|
10.2 |
1.6 |
0.344 |
101.6 |
3.6 |
8.76 |
|
13.5 |
1.8 |
0.522 |
108.0 |
3.6 |
9.33 |
|
17.2 |
1.8 |
0.688 |
114.3 |
3.6 |
9.90 |
|
21.3 |
2.0 |
0.962 |
133.0 |
4.0 |
12.8 |
|
26.9 |
2.0 |
1.24 |
139.7 |
4.0 |
13.5 |
|
30.0 |
2.3 |
1.59 |
159.0 |
4.5 |
17.1 |
|
33.7 |
2.3 |
1.79 |
168.3 |
4.5 |
18.1 |
|
38.0 |
2.6 |
2.29 |
193.7 |
5.4 |
25.0 |
|
42.4 |
2.6 |
2.57 |
219.1 |
5.9 |
31.0 |
|
44.5 |
2.6 |
2.70 |
244.5 |
6.3 |
37.1 |
|
48.3 |
2.6 |
2.95 |
273.0 |
6.3 |
41.6 |
|
54.0 |
2.6 |
3.32 |
323.9 |
7.1 |
55.6 |
|
57.0 |
2.9 |
3.90 |
355.6 |
8.0 |
68.3 |
|
60.3 |
2.9 |
4.14 |
368.0 |
8.0 |
70.8 |
|
70.0 |
2.9 |
4.83 |
406.4 |
8.8 |
85.9 |
|
76.1 |
2.9 |
5.28 |
419.0 |
8.8 |
88.7 |
|
88.9 |
3.2 |
6.81 |
|
|
|
Una volta effettuata la scelta del diametro possiamo passare a stabilire l’effettivo valore della velocità media che precedentemente avevamo posto pari a 3m/s per poterci ricavare un valore sensato del diametro del tubo. Per cui:
![]() (26)
(26)
Dalla consultazione delle opportune tabelle posso ricavarmi che per l’acqua a 15°C valgono i seguenti valori:
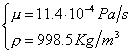 (27)
(27)
A questo punto sono in possesso di tutti i valori necessari per ricavarmi il numero di Reynolds e di conseguenza per determinare a che tipo di moto vado incontro.
![]() (28)
(28)
Per valori così elevati del numero di Reynolds il moto è ovviamente turbolento per cui, dopo esserci ricavati il valore della scabrezza relativa dovremo ricorrere al diagramma di Moody. Valutiamo la scabrezza relativa:
![]() (29)
(29)
Se ora andiamo a consultare il diagramma di Moody ricaviamo un fattore d’attrito x= 0.024.
Per la piccola differenza di altezza fra le sezioni 1 e 2 e considerando il fluido nel serbatoio 1 stagnante possiamo eliminare dall’equazione di bilancio il termine che tiene conto della velocità del fluido in ingresso e il termine che tiene conto della differenza di altezza fra le sezioni considerate giungendo così all’equazione:
![]() (30)
(30)
Dove R può essere espressa come la sommatoria delle perdite concentrate e delle perdite distribuite del condotto.
![]() (31)
(31)
Infatti in questo caso siamo in presenza di perdite concentrate oltre che distribuite, dovute agli ostacoli che il fluido incontra lungo il condotto, in questo caso abbiamo in totale 4 gomiti a 90°, 2 gomiti dolci, 2 valvole a sfera aperte e 1 filtro a maglia larga. Per ogni tipo di ostacolo è possibile determinare un coefficiente b dalle opportune tabelle che, una volta sostituito nella relazione precedente permettere di calcolare il valore di R.
![]() (32)
(32)
Sostituendo perciò tutti i valori numerici nella (30) avremo:
![]() (33)
(33)
Da cui moltiplicando per r otteniamo:
![]() (34)
(34)
Conoscendo la prevalenza della pompa e la portata in volume siamo ora in grado di calcolare la potenza erogata dalla pompa verso il fluido che quindi risulterà:
![]() (35)
(35)
Quindi considerando il rendimento della pompa h =0.5, vediamo che la potenza effettiva della pompa sarà approssimativamente di 110 KW, valore per niente trascurabile che richiederà un’accurata scelta del tipo di pompa per non incorrere in problemi. Dal punto di vista economico, visti i valori delle potenze in gioco, sarebbe meglio ricorrere a pompe con un rendimento superiore a 0.5 considerando che risparmiando sui costi energetici potremmo tranquillamente arrivare a coprire le spese sostenute per una pompa di maggior rendimento e quindi tecnologicamente più avanzata e ovviamente più costosa.