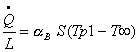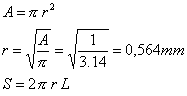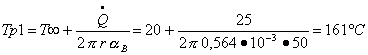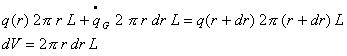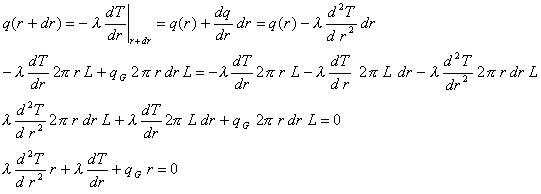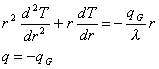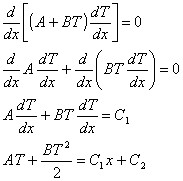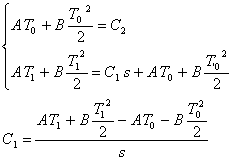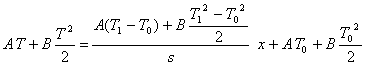UNIVERSITA’ DEGLI STUDI DI PARMA

Facoltà di ingegneria

Anno accademico 2000-2001

Corso di Fisica Tecnica

Docente: prof. Angelo Farina

Lunedì 11 dicembre 2000-parte prima

Elaborato di Francesco Pedrielli

Matricola n° 125184

Argomenti della lezione:

-Enunciato e spiegazione dell’equazione di Fourier

-Risoluzione di 3 esercizi sulla conduzione del calore

In fluidodinamica l’equazione differenziale di secondo ordine detta di Navier che definisce la viscosità, è ricavata dalle leggi di Newton. Analogamente in acustica, sempre dalla legge fondamentale del moto è stata ricavata l’equazione di Helmotz.

La legge di Forurier è un’equazione differenziale del 1° ordine che spiega il passaggio di calore come una conseguenza della differenza di temperatura tra la sorgente di calore e il ricevente. L’equazione di Fourier, invece, è del secondo ordine ed esprime il 1° principio della termodinamica. Si differenzia, però, da quest’ultimo perché mette in luce le modalità fisiche dello scambio del calore.

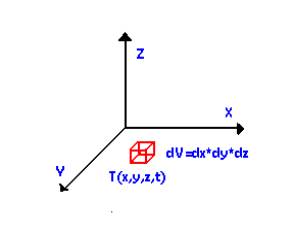
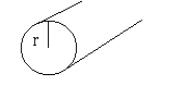
fig.1

Nel tempo infinitesimo dt sul confine infinitesimo del volume rappresentato in fig. 1 si scambia una quantità di calore dQ a sua volta infinitesima che è l’effetto della variazione dell’energia interna.

Non c’è il termine –dL che compare nell’enunciato del 1° principio perché si considera la sostanza indeformabile, dunque non c’è lavoro di deformazione.

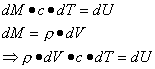
Il c che compare nell’ ultima relazione è, a rigore, il calore specifico a volume costante proprio per l’indeformabilità della sostanza.

Il primo membro esprime il dQ. Questo può, però, essere espresso come la somma del calore scambiato e di quello generato.

E questa è una novità! Fino ad ora si è considerato unicamente “il calore che va e quello che viene” ma mai “quello che c’è”.

Il calore generato può essere prodotto da:

-reazioni chimiche (calore di reazione)

-correnti elettriche (effetto joule)

-reazioni nucleari.

L’effetto joule è il processo più comune.

Questo calore non è proveniente dall’esterno.

Vediamo ora di quantificarlo

dove si misura in W/m³ ed è il lavoro generato nell’unità di tempo e di volume (è una quantità specifica riferita al volume che sta occupando).

Il fatto che il calore generato dipenda in questa relazione unicamente dal volume permette di affrontare fenomeni generativi come quelli nucleari che dipendono dallo spazio e non dalla massa.

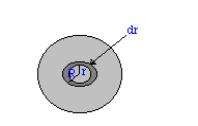
Analizziamo ora la quantità di calore scambiata al contorno: chiamo ds lo spigolo del cubo

Utilizzando il teorema di Gauss è possibile trasformare questo integrale di superficie in un integrale di volume ottenendo così la forma

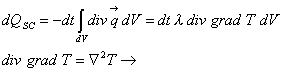
sostituendo e integrando ottengo

Dividendo per dt e riscrivendo sotto forma di derivata parziale arrivo alla forma

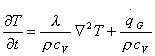
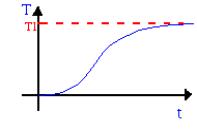
Questa è l’equazione di Fourier che governa la variazione di temperatura (T) nel tempo (t) in funzione del gradiente spaziale (ovvero a causa o degli effetti generativi o di trasporto di calore dovuto alla conducibilità del materiale).

Affronta, cioè, i transitori: prima potevamo analizzare soltanto flussi stazionari.

I problemi di transitorio termico si presentano quando un componente non è in grado di smaltire la potenza massima istantaneamente.

Si può fare un parallelo con un componente elettronico come il diodo: esso lavora in transitori periodici, dove si hanno cali periodici della temperatura che permettono al diodo di sopportare correnti maggiori perché dissipa continuamente calore.

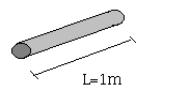
Facciamo ora un esempio:

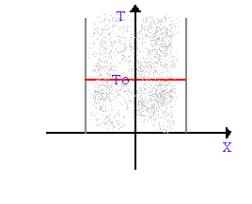
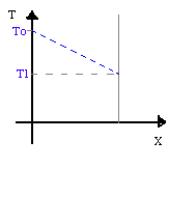
Se prendiamo una lastra di metallo e misuriamo la sua temperatura troviamo un valore . Studiamo ora come varia la temperatura all’interno dell’oggetto se lo immergiamo in un liquido a temperatura .

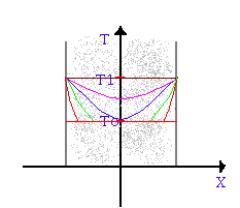
Inizialmente, dunque, se rappresentiamo graficamente la lastra su un sistema di assi cartesiani indicando sull’asse delle ascisse la posizione e sull’asse delle ordinate la temperatura che, in quella posizione, andiamo a misurare, si ottiene

fig.2

La temperatura è costante in tutte le posizioni della lastra e vale .

Ora studiamo la lastra immersa nel liquido a temperatura e osserviamo l’andamento della temperatura in funzione della posizione all’interno dell’oggetto.

fig.3

Le linee colorate rappresentano l’andamento della temperatura in diversi istanti di tempo: inizialmente la lastra assume la temperatura solamente sui bordi, successivamente anche i punti più interni si vengono a trovare a temperature più elevate. L’ultimo andamento della temperatura che si viene a ottenere è, così, una nuova linea orizzontale. Arrivati a questo punto, cioè, tutta la lastra avrà assunto la temperatura del liquido nel quale è stato immerso.

Se prendiamo un punto x’ all’interno della lastra e andiamo a diagrammare la sua temperatura nel tempo otteniamo una curva di questo tipo

fig.4

Dal grafico si evince chiaramente che il punto raggiunge la temperatura del liquido dopo un certo tempo. La presenza di un ritardo conferma l’esistenza di una velocità di propagazione del calore.

In acustica si era vista la presenza del termine velocità del suono all’interno delle equazioni fondamentali. Nell’equazione di Fourier, invece, il termine velocità di propagazione del calore non è presente. Questo dovrebbe far pensare che la velocità di propagazione del calore sia infinita, ma codesta è chiaramente una falsità.

Se si prendono elementi discreti di tratti della lastra e per ciascuno di questi si riscrivono le equazioni di bilancio dell’energia, si può, risolvendo il sistema, trovare una soluzione accettabile del problema.

Questo metodo detto delle differenze finite o di time marching discretizza l’asse dei tempi. Se divido l’oggetto in nodi spaziali, allora ogni nodo riceve informazione da un nodo vicino in un certo tempo. Questo implica l’introduzione di un passo temporale: si impone un limite alla velocità di propagazione del calore che porta così a far corrispondere il risultato numerico con quello sperimentale.

Spesso si hanno modelli analitici che non corrispondono al reale, con una corretta impostazione si riduce l’errore: si copre l’errore con un altro errore; è un metodo ingegneristico.

ESERCIZI

Ora verranno affrontati tre esercizi sulla propagazione del calore all’interno di solidi di diverso tipo.

Prima di procedere alla loro risoluzione verrà sotto riportata una utile tabella che esprime il coefficiente di conduttività termica di alcuni materiali in W/mC°

MATERIALE	CONDUT- TIVITA’ W/mC°	MATERIALE	CONDUT- TIVITA’ W/mC°
Alcool	0.21	Marmo	2.1-3.5
Alluminio	210	Mica	0.39
Argentana	27	Naftalina	0.37
Argento	420	Nichel	58-65
Asfalto	0.64	Oro	299
Basalto	1.27-3.5	Ottone	70-116
MATERIALE	CONDUT- TIVITA’ W/mC°	MATERIALE	CONDUT- TIVITA’ W/mC°
Bronzo	58-65	Pietra arenaria	1.30
Carbone	0.14-0.17	Piombo solido	35
Caucciù	0.13-0.23	Platino	70
Celluloide	0.35	Porcellana	0.80-1.05
Creta	0.90	Rame(8300kg/m³)	302
Duralluminio	160	Rame(8900kg/m³)	395
Sodio solido	125.60	Vetro	0.5-1
Stagno	64	Wood(lega)	12.78
Steatite	2.7	Zinco	110
Sughero(200 kg/m³)	0.052	Zolfo	0.23

1-Raggio critico dell’isolante

Prendiamo un filo composto da materiale conduttore elettrico che ipotizziamo essere rame. Esso dissipa calore per effetto joule se percorso da corrente.

Ci proponiamo di trovare la temperatura Tp di parete del filo nel caso esso non sia isolato e nel caso sia, invece, ricoperto da una guaina isolante.

fig.5

Indichiamo con Tp1 la temperature di parete del filo nel caso esso non sia isolato e con Tp2 la sua temperatura nel caso esso sia avvolto da una guaina isolante.

Sappiamo che:

il coefficiente di convezione esterno αB=50W/m²K

la sezione A=1mm²

la corrente I=5 A

la resistenza elettrica del filo per unità di lunghezza R’=1Ω/m

la temperatura dell’aria lontana dal filo t∞=20°C

e la sua lunghezza L=1m

Troviamo la potenza dissipata per unità di lunghezza

dato che la potenza viene dissipata per convezione allora si ottiene che

S indica l’area della “pelle” del filo attraverso la quale avviene lo scambio termico

Calcoliamo il raggio del filo:

fig.6

E’ evidente che la temperatura è troppo elevata: vediamo dunque come, attraverso, l’aggiunta di una guaina isolante è possibile ridurre la temperatura Tp2 di parete del filo.

Lo spessore della guaina dipende dalla conducibilità del filo λ=1 W/mK. Il nostro scopo è quello di ottenere il massimo scambio termico possibile, quindi dobbiamo trovare il raggio critico.

Esso si ricava mediante la relazione:

A prima vista sembrerebbe un risultato un po’ assurdo rispetto alla larghezza del filo di rame ma bisogna considerare la sua elevata conducibilità termica.

Eseguiamo ora una rappresentazione mediante resistenze del filo in sezione:

fig.7

R1 ed R2 sono le resistenze termiche, mentre r1 e r2 sono rispettivamente il raggio del filo di rame e il raggio della guaina isolante. Abbiamo calcolato il valore di r2 ponendolo uguale al raggio critico. Chiamiamo dunque il raggio dell’isolante e il raggio del filo di rame .

è la resistenza di conduzione della guaina isolante

Mentre la resistenza di convezione dovuta all’aria esterna è

Otteniamo che il salto di temperatura tra il filo conduttore e l’aria sarà

Ovvero aumenta così tanto la superficie di scambio che diminuisce la temperatura anche se ho una resistenza termica in più.

E’ anche possibile calcolare la temperatura esterna sulla gomma applicando la legge di Ohm alla resistenza esterna per trovare la differenza tra la temperatura della gomma e quella dell’aria.

Questa è, dunque, la temperatura sulla guaina isolante.

2°esercizio

Ci proponiamo ora di studiare come evolve la temperatura all’interno del conduttore. Stavolta, però, supponiamo di utilizzare come materiale dell’acciaio inox che compone un tubo sapendo che:

fig.8

Una possibilità sarebbe utilizzare l’equazione di Fourier moltiplicandola per il termine generativo. Altrimenti possiamo seguire un’altra strada:

del nostro tubo conduttore studiamo un cilindretto vuoto ricavato dal conduttore stesso.

fig.9

R=r+dr

A questo punto possiamo ragionare a regime stazionario su quel cilindretto se consideriamo dr infinitesimo.

Il primo membro indica la potenza generata, il secondo quella che lascia il cilindretto infinitesimo.

Vediamo ora di espletare la precedente relazione

dalla legge di Fourier

sostituendo

Risoluzione non affrontata a lezione:

moltiplicando per r si ottiene

e dividendo per λ diverso da 0

Cambiando notazione si ottiene

Nel caso che stiamo affrontando è lecito porre T>0 e, quindi, x>0

Eseguiamo il cambiamento di variabile cioè

Posto si ha , da cui

,

L’equazione si trasforma così in un’equazione a coefficienti costanti

ossia

da cui

, e con

Si ottiene infine

che equivale a

3°esercizio

Considero una parete con λ variabile regolarmente con la temperatura. Lo studio deve avvenire in condizioni stazionarie e in assenza di sorgenti termiche.

Chiaramente in questo caso non ci sarà effetto joule.

fig.10

La temperatura varia da a in maniera non lineare in quanto λ varia al variare della temperatura. Se λ fosse costante allora il tratto che collega i 2 punti a diversa temperatura e posizione sarebbe lineare.

Vediamo ora di applicare l’equazione di Fourier, dalla quale otteniamo che

questo perché siamo in condizioni stazionarie. Inoltre avremo che

A questo punto poniamo λ=A+BT e l’andiamo a sostituire nella relazione precedente ottenendo:

Applichiamo ora le condizioni al contorno sostituendo

la prima volta e

la seconda otteniamo il seguente sistema di equazioni:

Arriviamo dunque alla forma finale

La funzione che otteniamo è del tipo x=f(T) ed è una parabola con asse di simmetria parallelo a quello delle ascisse.

Vediamo di studiare ora le caratteristiche del grafico:

-La concavità è verso sinistra quando B>0. Con la maggior parte dei materiali si presenta questa situazione.

-Se fosse B=0 allora la relazione si ridurrebbe all’equazione di una retta.

-La concavità è verso destra quando B<0

Le considerazioni geometriche fatte sopra si traducono in termini di conduttività: la concavità verso sinistra descrive la situazione in cui al crescere di T cresce anche la conduttività. Viceversa la concavità verso destra descrive la situazione in cui, al crescere di T, la conduttività diminuisce. La retta congiungente i due punti d’intersezione delle parabole con concavità opposte descrive, invece, la situazione in cui la conduttività rimane costante.

fig.11

Nel costruire dei sistemi di raffreddamento si fanno i conti tenendo λ costante, perché il fatto che esso sia variabile porta ad un aumento della dissipazione del calore. Nel progettare è sempre meglio adottare un ottimo margine di sicurezza e questo metodo è adatto a questo scopo.