ESERCIZIO 1 (scatolone
adiabatico)
ESERCIZIO 2,ESERCIZIO 3 (problemi che riguardano la determinazione
del titolo)
ESERCIZIO 4 (la caldaia)
ESERCIZIO 5 (la pentola a
pressione)
Scatolone
adiabatico
Consideriamo uno scatolone
adiabatico, sistema chiuso termicamente isolato di cui fanno parte due
scompartimenti separati sia dal punto di vista termico che meccanico da un
divisorio isolante (vedi fig.1).
A destra e a sinistra del
divisorio si ha vapore d’acqua saturo: nello scompartimento (A) 1 kg alla
pressione di 9.8 bar, mentre nell’altro si
trovano 2 kg alla pressione di 0.98 bar. Determinare pressione e titolo
finali del gas dopo aver rimosso il divisorio, sapendo che il titolo del vapore
d’acqua nello scompartimento (A) xA vale 0.1 e quello
nello scompartimento (B) xB vale 0.5.
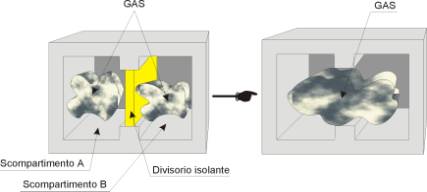
-Figura
1-
Soluzione
Innanzi tutto prima di
procedere nella soluzione analitica del problema notiamo che è importante avere
già una conoscenza per lo meno spannometrica del valore finale che ci si
aspetta dai dati del problema. Una stima approssimativa del risultato è di grande aiuto quando ci si
trova, come in questo caso, di fronte ad uno dei classici problemi che sono
fisicamente ben posti ma algebricamente insolubili; ipotesi normale nella
stragrande maggioranza di casi pratici, dove non si può di fatto arrivare ad
una soluzione in forma chiusa del tipo:
![]()
![]()
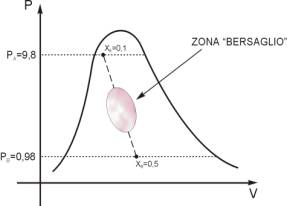
-Diagramma pV del gas-
Non appena viene tolto il
setto la situazione che si presenta è
quella di una massa MC data dalla somma delle due masse dei
gas contenuti nei due scompartimenti inizialmente separati:![]()
![]()
![]()
Poniamo le condizioni dello
stato fisico finale:
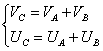
![]()
La (2) può essere espressa
con la legge dei vapori saturi (introducendo la combinazione lineare del volume
specifico e di quello differenziale)per cui:
![]()
![]()
![]()
![]()
Sostituendo (4) e (5) in (2) si ha :
![]()
![]()
dove ![]() ,
,
ed il volume differenziale è calcolabile come ![]() ,(il valore si ricava comunque in Appendice).
,(il valore si ricava comunque in Appendice).
Numericamente sostituendo i valori dei volumi ricavati
dalle tabelle si ottiene:
![]()
![]()
che sappiamo essere uguale a:
![]()
![]()
Analogamente
a quanto fatto per la (2), ricaviamo le energie interne iniziali dei due gas:
![]()
![]()
![]()
![]()
L’energia interna
differenziale è calcolabile in generale come:
![]()
![]()
dove p è la pressione del
vapore saturo, per il gas nello scompartimento A PA=9,8 bar, per quello nello
scompartimento B PB=0,98 bar
A questo punto utilizzando
la (11) ed i valori che si ricavano dalle tabelle siamo in grado di calcolare
le energie interne differenziali e con queste l’energia interna dei gas
contenuti nei due scompartimenti. Sostituendo quindi (9) e (10) in (3) si ha:
![]()
![]()
Tale valore sappiamo essere uguale a:
![]()
![]()
Riconsiderando (8) e (13) si giunge al seguente
sistema:
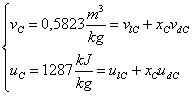
![]()
Questo sistema nell’unica
incognita xC è insolubile se non adottando metodi di
calcolo numerico, tra i quali ricordiamo quello a tentativi (o di Montecarlo)
tramite il quale si attribuiscono valori random
ai volumi specifici della prima equazione per ricavare xC.
Tale valore viene successivamente sostituito nella seconda equazione
per verificarne l’identità; questo metodo di facile applicazione per un
calcolatore diviene impraticabile manualmente. Si può allora pensare di
utilizzarne uno iterativo a tentativi guidati. Grazie a questo si parte da un certo valore di pressione a cui
corrispondono due valori (tabellati) dei volumi vlC e vdC della prima equazione di (14), dopodiché il
valore incognito di xC che si ricava lo si sostituisce nella seconda equazione del
sistema per verificare la corrispondenza tra il valore di uC appena dedotto e quello invece effettivo.
A questo punto siamo in grado di controllare a quale distanza ci troviamo dalla
soluzione, questo tentativo fornisce un’indicazione per le iterazioni
successive. Il metodo iterativo scelto deve
essere consistente. Effettuare un’interpretazione spannometrica diventa
ora necessario per poter partire da un valore il più possibile prossimo alla
soluzione.
Dopo una prima osservazione
all’intervallo considerato nel diagramma pV, prendiamo come dato iniziale
un valore di pressione pari a 294 Kpascal( 2,94 bar ).
Ricaviamo dalle tabelle i
valori corrispondenti di vlC e vdC e
sostituiamoli nella prima equazione di (14), si ricava un valore di xc
pari a 0,94.
Tale risultato viene
sostituito nell’ altra equazione di (14) ricavando un valore di uc pari a 2425 kJ/kg, piuttosto
lontano dal dato di partenza (1287 kJ/kg); si sceglie allora un nuovo valore di
pressione e si rieseguono i passi descritti in precedenza.
Di seguito sono tabulati i
risultati delle iterazioni per i diversi valori di pressione
|
Pressione(kPa) |
xc |
Uc |
|
294 |
0,94 |
2425 |
|
196 |
0,55 |
1820 |
|
147 |
0,49 |
1472 |
|
118 |
0,40 |
1266 |
xc:titolo
del gas che si ricava dalla prima equazione del sistema
uc:energia
interna specifica del gas che si ricava dalla seconda equazione
La seconda iterazione ci
permette di riconoscere se ci si allontana o meno dal valore esatto di uC ricavato dall’equazione (3)
del sistema di partenza. Avuta conferma che abbassando il valore della
pressione si converge al valore esatto, nelle due successive iterazioni ci si
accorge di aver fatto forcella (il
valore ricercato è posizionato tra i due di uC appena
ottenuti).
Si osserva inoltre che
l’ultimo risultato ottenuto è particolarmente vicino al bersaglio, la pressione
del gas nel suo stato fisico finale sarà di poco superiore ai 118 Kpascal.
Nota: anche partendo da un valore centrato nella zona
bersaglio si osserva che comunque la soluzione si discosta dalla previsione.
Negli impianti che
funzionano a vapore ci sono zone in cui
tramite appositi strumenti (manometri e termometri) è possibile determinare
pressione e temperatura del gas, ma per il titolo?
Problemi che riguardano la determinazione del titolo:
Si consideri la figura
seguente fig.(1) dove si ha un calorimetro ed un recipiente; il
calorimetro è un vasetto di vetro (sembra un termos) isolato termicamente.
Questo fatto è dovuto al doppio strato di vetro al cui interno essendo stato
fatto il vuoto non è possibile scambiare calore con l’esterno. Il contenitore è
sigillato da uno strato di sughero che presenta due piccole aperture. In una
viene inserito un sottile termometro, nell’altra viene collocato un tubicino
all’interno del quale fluisce del vapore d’acqua dopo l’apertura di un
rubinetto che mette in comunicazione il calorimetro con il recipiente. Questo
contiene 0,045 kg di gas alla temperatura Tv di 100°C
e alla pressione Pv di 1 bar.
All’interno del calorimetro sempre alla pressione di
1bar, ma alla temperatura Tc
di 25 °C e’ contenuta una massa Mc pari a 0,35 kg
d’acqua.
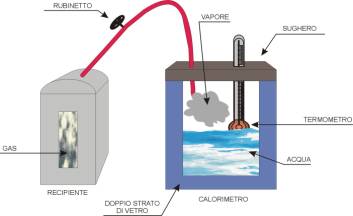
-Figura 1-
Dopo il versamento e la
condensazione del vapore saturo all’interno del calorimetro, si perviene a
0,395 kg d’acqua e ad una temperatura Tfin
di 64°C.
Si chiede quale era il
titolo iniziale del vapore nel recipiente.
L’ aumento di temperatura
misurato dal termometro non può essere totalmente imputato alla variazione di
energia interna dell’acqua, il che equivarrebbe ad attribuire al vetro una
capacità termica nulla. Allora solitamente il costruttore fornisce sul fondo
del calorimetro una massa equivalente fittizia Mf di acqua pari a 0,22 kg con la
caratteristica di avere la solita capacità termica del vetro.
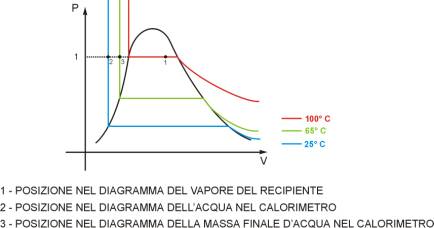
-Diagramma
pV del calorimetro-
Soluzione:
Si ipotizza che inizialmente
all’ interno del calorimetro vi sia una massa data da:
![]()
![]()
Alla fine del processo
quello che è rimasto costante è la pressione.
Il sistema ha si compiuto
lavoro verso l’esterno, ma il lavoro netto è nullo.
Per procedere alla soluzione
si scrive l’equazione di primo principio in forma entalpica
![]()
![]()
![]()

ovvero:
![]()
![]()
L’entalpia finale è funzione
dell’acqua contenuta nel calorimetro nello stato finale; mentre l’entalpia
iniziale è data dalla somma dei contributi dell’entalpia dovuta alla massa Ml
(massa di liquido contenuta inizialmente nel calorimetro)e alla massa di vapore
d’ acqua saturo nel recipiente Mv.
Per cui:
![]()
![]()
dove:
![]()
![]()
![]()
calore specifico dell’acqua(CL=4,187
kJ/kg°K)
con la massa finale data
dalla massa contenuta nel calorimetro più la massa di vapore condensato
versatogli dentro:
![]()
![]()
Numericamente:
![]()
![]()
per l’entalpia dell’ acqua:
![]()
![]()
![]()
per
il vapore si ha invece:
![]()
![]()
![]()
![]()
con hvap
entalpia specifica del vapore saturo, hl entalpia specifica
del liquido alla solita pressione, x il titolo che si vuole
determinare ed r calore latente di vaporizzazione (anche definito
come hd entalpia specifica differenziale).
Sostituendo
queste espressioni nella (4) si trova un’equazione nella sola incognita
x:
![]()
![]()
da cui si ricava che il
titolo vale:
![]()
![]()
2° metodo per
la determinazione del titolo
Supponiamo di avere un tubo che
porta del vapore saturo ad una turbina fig.(1).
Tramite un apposito
strumento detto manometro misuriamo la pressione all’interno del tubo
ricavandone il valore di 28 bar (pressione a cui sappiamo corrispondere una
temperatura del vapore saturo di 230°C ).
Il problema è determinare
il titolo x del vapore nel tubo.
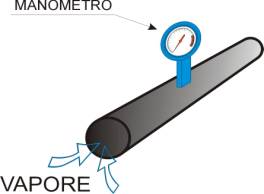
-Figura 1-
Possiamo giungere ad una
soluzione sperimentale del quesito allacciando al tubo tramite un piccolo foro
una conduttura in grado di sfiatare il gas all’esterno per mezzo di una valvola
di sfogo. Vicino a questa fig.(2) si pone un termometro per misurare la
temperatura del vapore in uscita; sperimentalmente si fornisce il dato di
115°C.
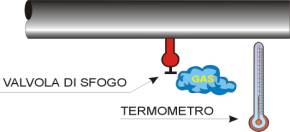
-Figura 2-
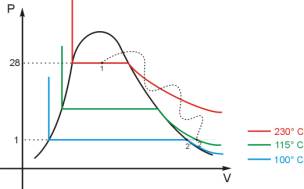
-Diagramma
pV dell’uscita del vapore dal tubo-
Soluzione:
Il vapore fuoriesce subendo
una trasformazione irreversibile di dissipazione di energia (tratteggio ![]() nel diagramma pV )
per cui il calore scambiato con l’esterno non è certamente nullo, come del
resto il lavoro perché la velocità con cui il gas sfiata mette in gioco
dell’energia cinetica.
nel diagramma pV )
per cui il calore scambiato con l’esterno non è certamente nullo, come del
resto il lavoro perché la velocità con cui il gas sfiata mette in gioco
dell’energia cinetica.
L’equazione che mi fornisce
il bilancio energetico per un sistema aperto è la seguente:
![]()
![]()
Sotto l’ipotesi che il
vapore esca dalla valvola controllato da un processo di laminazione
isoentalpica ovvero così lentamente da poter considerare nulle sia le perdite
dovute all’ energia cinetica sia quelle dovute alla produzione di calore:
Si può riscrivere la (1)
come:
![]()
![]()
Dall’uguaglianza delle entalpie specifiche si può
ricavare il titolo infatti:
![]()
![]()
![]()
![]()
dove si è sfruttato:
![]()
In (3) e (4) hl1
e hl2 sono le entalpie specifiche del liquido
alla pressione rispettivamente di 28 bar e 1 bar, r1 e r2 calori latenti di vaporizzazione. Nella (4)
si è utilizzato il valor medio del cpvap perché esso è
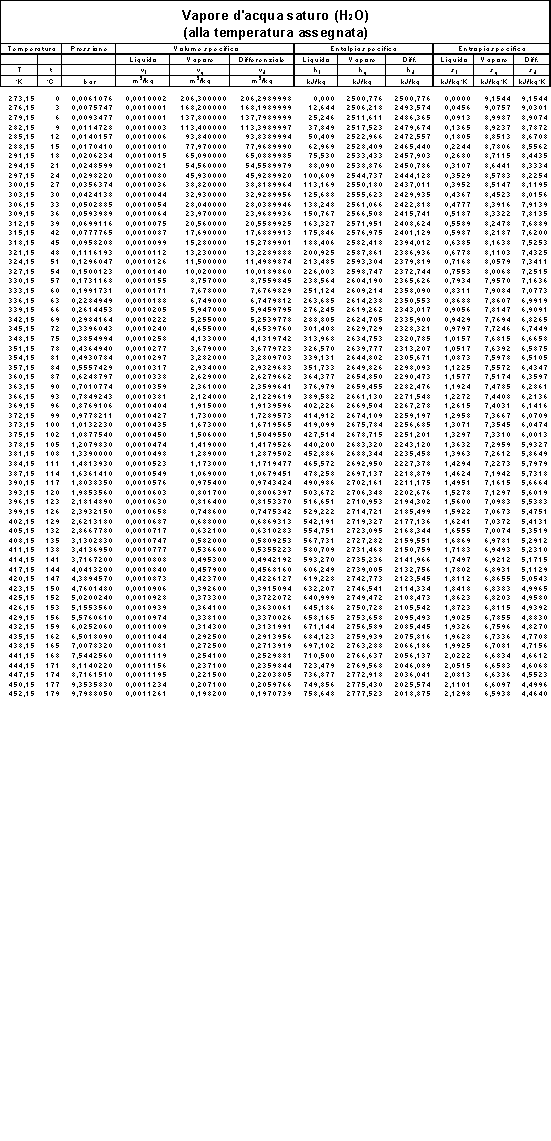
in generale dipendente dalla temperatura(vedi tabella per vedere la variazione del cp del
vapore d’acqua surriscaldato alla pressione di 1 atmosfera=0,980665 bar); in
questo caso essendoci un piccolo salto di temperatura (5°C) si è presa una
sorta di media aritmetica:
![]()
![]()
calore specifico medio(cpm)del vapore
d’acqua surrisc.
(misurato alla temperatura di saturazione alla
temperatura assegnata)
|
Pressione P=1
atmosfera |
||
|
Temperatura |
cpm |
|
|
°C |
°K |
kJ/kg°K |
|
110 |
383,15 |
2,022 |
|
120 |
393,15 |
2,043 |
|
130 |
403,15 |
2,015 |
|
140 |
413,15 |
2,005 |
|
150 |
423,15 |
1,998 |
|
160 |
433,15 |
1,993 |
|
170 |
443,15 |
1,991 |
Sostituendo (3) e (4) in (2)
con i corrispondenti valori che si ricavano dalle tabelle
si ottiene:
![]()
![]()
da cui:
![]()
![]()
La caldaia
Osserviamo il diagramma [pV]
che schematizza il funzionamento di una caldaia fig(1):
-Simbolo caldaia-
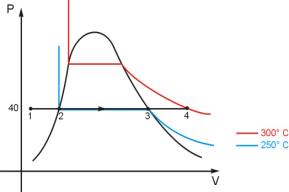
-Diagramma
pV della caldaia-
L’acqua entra in caldaia
tramite una pompa alla temperatura T1 di 60°C (punto 1 del
grafico) e alla pressione P1 di 40 bar.
Mantenendo costante la
pressione l’acqua viene scaldata fino a raggiungere la condizione di
saturazione( 2 nella curva limite inferiore ). Alla pressione di
40 bar corrisponde una temperatura T2 di 250°C.
A questo punto avviene un
processo di vaporizzazione, tale trasformazione avvenendo su un isoterma
fornisce sempre il valore di temperatura T3 250°C, ma lo
stato fisico del liquido è passato alla fase di vapore saturo secco ( 3 nella
curva limite superiore ).
Fornendo ancora calore il
gas viene a trovarsi in una condizione di vapore d’acqua surriscaldato alla
temperatura T4 di 300°C( 4 ).
Si vuole calcolare la
quantità di calore Q che bisogna fornire al sistema per surriscaldare
una massa d’acqua di 1 kg.
Soluzione:
Dato che la massa è unitaria
![]() .
.
Procediamo nella soluzione
tramite l’equazione di bilancio dell’energia per i sistemi aperti per cui:
![]()
![]()
dove:
![]()
![]()
infatti l’integrale mi
fornisce in questo caso l’area sottesa dalla curva del cambiamento di stato
rispetto all’asse delle ordinate, ma la proiezione della curva sull’asse è un
insieme a misura nulla per cui non sottende alcuna area, allora (1) diventa:
![]()
![]()
Consideriamo ora i
contributi delle varie fasi al calcolo della variazione di entalpia:
![]()
1° fase: Riscaldamento
dell’acqua liquida
La variazione di entalpia è uguale alla variazione di
temperatura moltiplicata per il calore specifico dell’acqua (in questo caso può
essere sostituito da cp poiché la trasformazione
avviene lungo un’ isobara quindi a pressione costante):
![]()
![]()
2°fase: Passaggio dalla fase
di liquido a quella di vapore saturo secco
Tale salto di entalpia equivale alla differenza tra
l’entalpia del vapore saturo secco e quella del liquido alla solita pressione:
![]()
![]()
3°fase: passaggio da vapore
saturo secco a vapore surriscaldato
Questo corrisponde al salto entalpico per portare il
vapore dalla curva limite superiore in cui si trova allo stato di vapore saturo
secco alla fase di vapore surriscaldato:
![]()
![]()
calore specifico medio del vap. d’acqua surr.
(misurato dalla
temperatura di sat. alla temp.assegnata)
|
Pressione P= 40 atm |
||
|
Temperatura |
cpm |
|
|
°C |
°K |
kJ/kg°K |
|
260 |
533,15 |
3,483 |
|
280 |
553,15 |
3,262 |
|
300 |
573,15 |
3,136 |
|
320 |
593,15 |
3,027 |
|
340 |
613,15 |
2,931 |
Si ricava il valore di cpvap
pari a 3,1 kJ/kg°K
Sostituendo i valori
corrispondenti la (1) diventa:
![]()
![]()
Pentola a pressione
Si consideri una pentola a
pressione fig.(1) riempita con 11 litri di acqua e la si ponga sul fuoco.La temperatura del
liquido comincerà a salire fino a raggiungere quella di ebollizione Te=100°C
(supponendo di eseguire l’esperimento alla pressione atmosferica).
Mantenendo la pentola sul
fuoco, all’interno di questa comincerà a formarsi del vapore. La pentola inizia
allora a sfiatare fino a che non viene
chiusa la valvola fig(2).Nella situazione finale all’interno del
contenitore sigillato si trovano ancora 10 kg di liquido e 1 kg di vapore
d’acqua saturo.
Si chiede quanto calore è
necessario per portare la pressione all’interno della pentola dal valore
iniziale di 1 bar(valvola chiusa) a quello di 5.
Fig.1 Fig.2
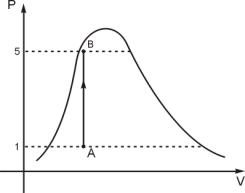
-Diagramma pV della pentola
a pressione-
Soluzione:
Calcoliamo innanzitutto il titolo xA del vapore nello stato iniziale che ci sarà utile nei calcoli:
![]()
dove MTOT è la massa d’acqua più la massa di vapore saturo contenuta nella pentola e MVAP è la massa di vapore in equilibrio con il liquido.
Utilizziamo il primo principio della termodinamica:
![]()
![]()
Dato che la pentola è un sistema chiuso (valvola abbassata) il lavoro L è esprimibile come:
![]()
Ma questo integrale è nullo poiché il contenitore è
indeformabile e l’aumento di temperatura non può quindi far espandere il gas.
Allora (1) diventa:
![]()
![]()
Sappiamo esistere poi una relazione tra l’energia
interna specifica del vapore e le energie specifiche del liquido alla solita
pressione:
![]()
![]()
![]()
![]()
dove udA e udB sono le energie specifiche differenziali.
A questo punto l’unico termine incognito è il titolo xB; esso è calcolabile poiché la trasformazione avviene su un’isocora per cui il volume del gas nei due stati iniziale e finale è identico, allora:
![]()
![]()
da cui si ricava
che il titolo nello stato finale vale:
![]()
![]()
![]()
![]()
Si possono calcolare ora uA e uB:
![]()
![]()
![]()
![]()
Allora (2) diventa:
![]()
![]()
Appendice back to top