Guglielmetti Marco nº matricola 105105 Lezione del 19/12/2000 - ore 14:30 – 16:30
Scambiatori di Calore
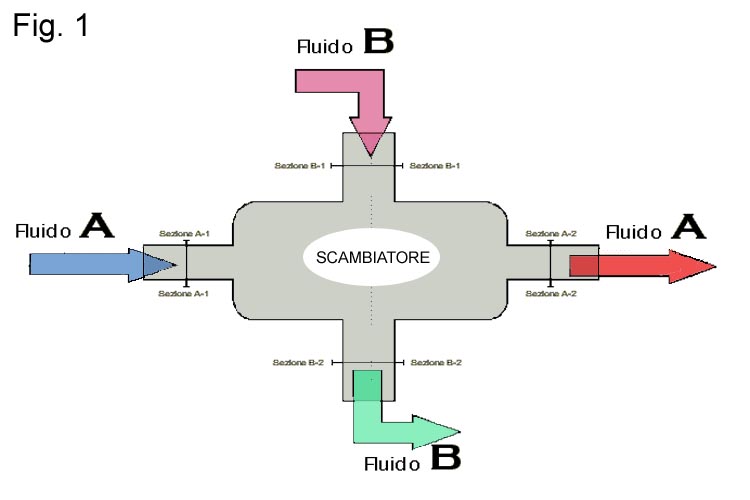
Gli scambiatori di calore sono sistemi aperti adibiti al trasferimento di energia, sotto forma di calore, tra due fluidi a diversa temperatura. Lo scambio termico avviene grazie ad una parete metallica che separa i due fluidi.
Il fluido A viene detto fluido di processo, mentre il fluido B viene detto fluido di servizio. Il contatto fra i due fluidi dipende dalla "pulizia" del fluido di servizio: a seconda del fatto che sia sporco o pulito si avrà nel primo caso uno scambiatore con una "parete" che evita il contatto chimico tra i due fluidi, e’ il caso dei diversi processi alimentari; nel secondo caso un esempio e’ quello della pastorizzazione del latte, A e B possono venire in contatto per poi separarsi finito il processo. Gli scambiatori a contatto pero’ vengono usati più raramente, inoltre il loro studio e’ notevolmente più complicato.

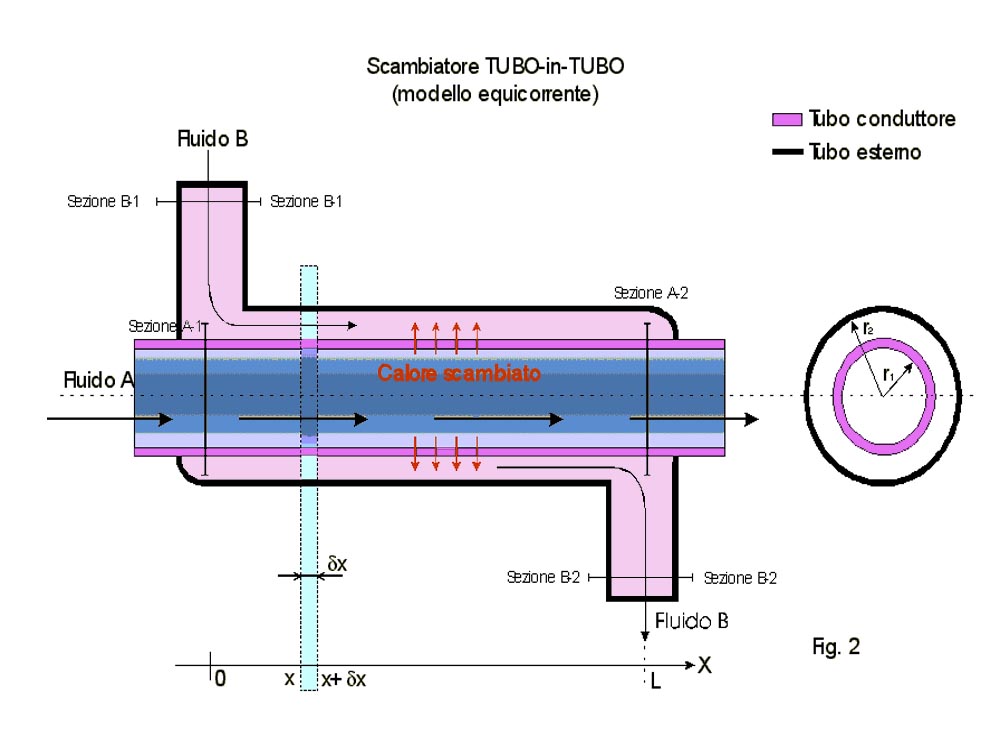
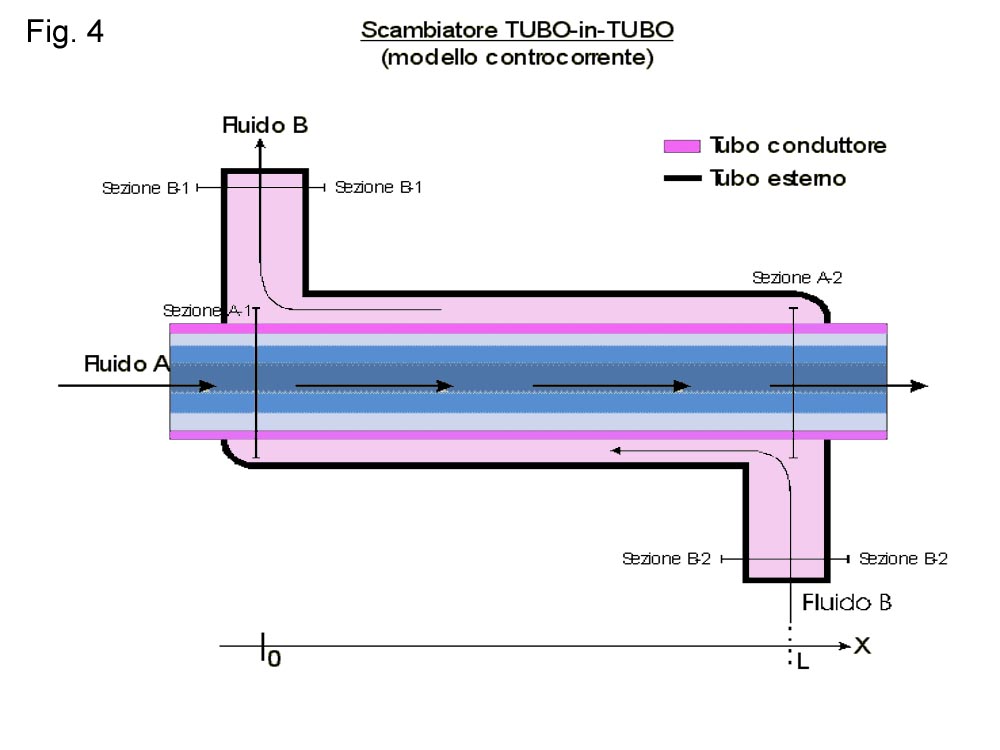
Lo scambiatore di calore tubo in tubo e’ formato da due tubi concentrici, in cui passano due fluidi a temperature diverse. Il tubo più interno e’ costituito da materiali ad alta conducibilità termica, che consentono lo scambio più alto possibile di calore tra i due fluidi. Il materiale più indicato per questo uso e’ l’ acciaio che offre un’ alta resistenza all’ usura; con l’ acciaio inox lucidato e’ inoltre particolarmente semplice la pulizia della parete interna del tubo, si evitano incrostazioni, quindi nei settori in cui l’ igiene e’ importante e’ il più indicato. Per il tubo esterno i materiali più adatti sono metalli a bassa conducibilità termica, anche se non necessariamente isolanti.
Questo tipo di scambiatore presenta un estrema facilità di calcolo per quanto riguarda il dimensionamento della superfici di scambio e della quantità di calore scambiato, per cui ne permette il calcolo esatto delle caratteristiche. Risulta pero’ essere molto costoso a causa del materiale del tubo interno ed ingombrante rispetto alla potenza termica dissipata: e’ un vantaggio possederlo solo nel caso in cui sia necessaria un’ estrema pulizia (settori alimentare e farmaceutico).
A seconda che il fluido di servizio entri o esca dalla sezione B1, si hanno due diversi tipi di scambiatori tubo in tubo : equicorrente e controcorrente.
Nel primo caso i due fluidi hanno lo stesso verso di scorrimento. Questo tipo di scambiatore fornisce un riscaldamento minore rispetto al secondo tipo di scambiatore, ma e’ più veloce quindi consigliato in processi che richiedono rapidità.
Nel caso di scambiatore controcorrente i due fluidi hanno verso opposto.
In entrambi gli scambiatori il fluido di processo entra ad una temperatura T1 e viene riscaldato fino ad una temperatura T2, ciò che chiaramente differenzia il processo e’ il comportamento del fluido di servizio.
Dal punto di vista del calcolo, infatti, bisogna distinguere il calcolo termico, chiamato anche dimensionamento delle superfici di scambio, dal calcolo energetico, basato unicamente sulle relazioni di primo principio (bilancio dell’entalpia tra i due fluidi). Il calcolo energetico si basa su un concetto fondamentale: tanto calore cede un fluido, tanto ne assorbe l’altro. Il calcolo termico, invece, richiede uno studio più approfondito, poiché richiede il calcolo dei coefficienti di convezione, delle resistenze termiche e il dimensionamento delle superfici di scambio. Si vengono a distinguere, perciò, due tipi di dimensionamento di uno scambiatore: quello energetico, piuttosto semplice, e quello termico, più complesso.
Il problema, quindi, è duplice. Da un lato possiamo valutare la potenza termica in termini di scambio termico:
![]() (1)
(1)
dove con ΔT viene indicata la differenza di temperatura tra i due fluidi e con RTOT la resistenza termica complessiva dello scambiatore.
Da un punto di vista energetico, posso scrivere la potenza termica in due modi equivalenti, uno riferito al fluido di processo, che chiameremo fluido A e che si sta riscaldando, e uno riferito al fluido di servizio, che chiameremo fluido B e che si sta raffreddando:
![]() (2)
(2)
dove con ![]() viene indicata la portata dei due fluidi e con 1 e 2 le sezioni, rispettivamente, di ingresso e di uscita dei due fluidi stessi.
viene indicata la portata dei due fluidi e con 1 e 2 le sezioni, rispettivamente, di ingresso e di uscita dei due fluidi stessi.
Dal punto di vista termico, quindi, sono presenti due problemi da risolvere: determinare il ΔT e determinare la RTOT.
Vediamo ora perché risulta difficile determinare la differenza di temperatura. Considerando lo scambiatore in equicorrente (entrambi i fluidi scorrono nella stessa direzione) in fig. 2, si può costruire un diagramma, in cui in ascissa si ha la distanza x, che arriva ad L (lunghezza dello scambiatore), mentre in ordinata si ha la temperatura. 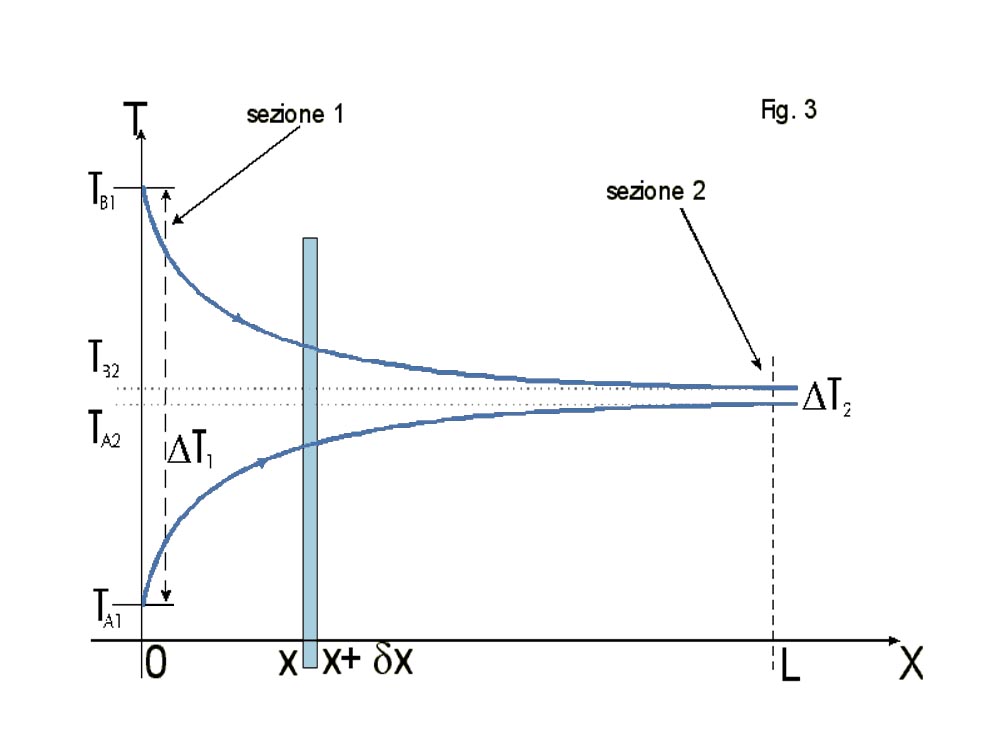
Notiamo un DT variabile, ovvero avremo un flusso termico fortemente variabile: in particolare, alla sezione 1, essendoci un DT= DT1 grande, il flusso termico tra i due fluidi sarà piuttosto vivace, mentre alla sezione 2, poiché il DT= DT2 è molto basso, il flusso termico sarà quasi nullo.
Data la natura così variabile di DT, siamo costretti, nello studio della potenza scambiata ![]() , a considerare in realtà un
, a considerare in realtà un ![]() (il suo valore medio), e di conseguenza un
(il suo valore medio), e di conseguenza un ![]() medio.
medio.
Consideriamo uno "scambiatore" infinitesimo di lunghezza δx, all’interno del quale possiamo ritenere l’andamento di ΔT praticamente lineare. Ottengo quindi una relazione, alla coordinata x:
![]() (3)
(3)
in cui RTot rappresenta la resistenza termica dello scambiatore infinitesimo e che possiamo rappresentare in questo modo:
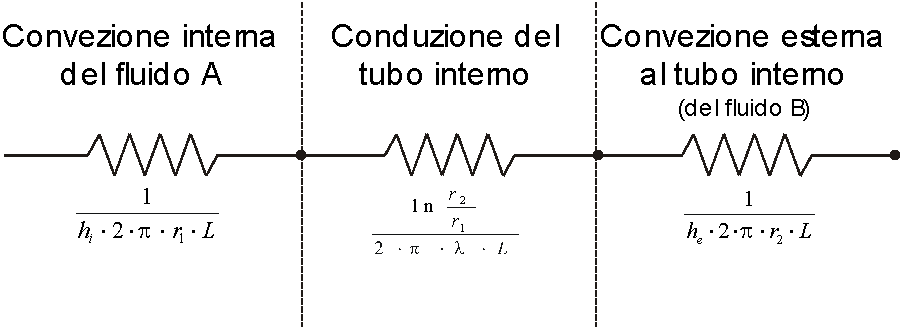
in cui: λ è la conducibilità termica del materiale con il quale è costruito il tubo interno,
hi è il coefficiente di convezione interno,
he è il coefficiente di convezione esterno,
L è la lunghezza dello scambiatore considerato, in questo caso δx.
La resistenza totale RTot è la somma dei tre termini (poiché la lunghezza dello scambiatore è infinitesima, si ottiene rapidamente che la resistenza termica risulta infinita).
Definiamo ora il coefficiente globale di scambio K in relazione alla superficie di scambio S come:
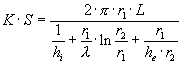 (4)
(4)
in cui K è strettamente legata alla superficie in cui avviene lo scambio S.
Possiamo quindi scrivere la RTot per unità di superficie come: ![]() (5)
(5)
per cui otteniamo: ![]() (6)
(6)
e conseguentemente: ![]() (7)
(7)
ovvero il ![]() (che è un infinitesimo: compare infatti il δx a numeratore) in funzione di [TB-TA] .
(che è un infinitesimo: compare infatti il δx a numeratore) in funzione di [TB-TA] .
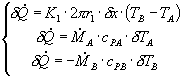 (8)
(8)
in cui si nota subito il carattere infinitesimo anche dei secondi membri. Si è, quindi, formulata tre dipendenze di ![]() dalle temperature TA e TB. E’ possibile scrivere un’unica equazione che descrive la dipendenza di
dalle temperature TA e TB. E’ possibile scrivere un’unica equazione che descrive la dipendenza di ![]() dalla differenza tra le due temperature. Per far ciò, è necessario ricavare dTA dalla seconda equazione di (8) e dTB dalla terza, ottenendo:
dalla differenza tra le due temperature. Per far ciò, è necessario ricavare dTA dalla seconda equazione di (8) e dTB dalla terza, ottenendo:
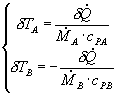 (9)
(9)
Facendo differenza membro a membro, si ricava:
![]() (10)
(10)
in quanto la differenza dei differenziali è il differenziale delle differenze. Questa è, dunque, un’equazione nell’unica incognita d(TA–TB). Al posto di ![]() si scrive il suo valore dalla prima equazione di (8):
si scrive il suo valore dalla prima equazione di (8):
![]() (11)
(11)
Si ottiene pertanto un’equazione differenziale di primo grado a variabili separabili. Separando le variabili e integrando:
![]() (12)
(12)
Da cui:
![]() (13)
(13)
Ciò che si voleva ricavare era, tuttavia, un’espressione di ΔTMEDIO semplice ed immediata. Per ottenere ciò, si osserva che a secondo membro si trova il prodotto K1S1, che diventa:
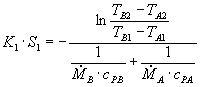 (14)
(14)
Per avere una dipendenza solo dalle temperature, dalle equazioni (2) si ricava:
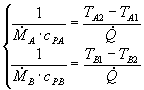 (15)
(15)
Sostituendo le (15) nella (14):
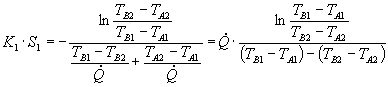 (16)
(16)
da cui, sostituendo la (16) in ![]() :
:
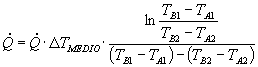 (17)
(17)
si ottiene immediatamente il valore di ΔTMEDIO logaritmico cercato, che diventa:
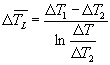 (18)
(18)
Consideriamo ora uno scambiatore in controcorrente, schematizzabile in questo modo:
poiché l’entrata del fluido B avverrà alla sezione 2, dove invece il fluido A esce, avremo una situazione di questo tipo:
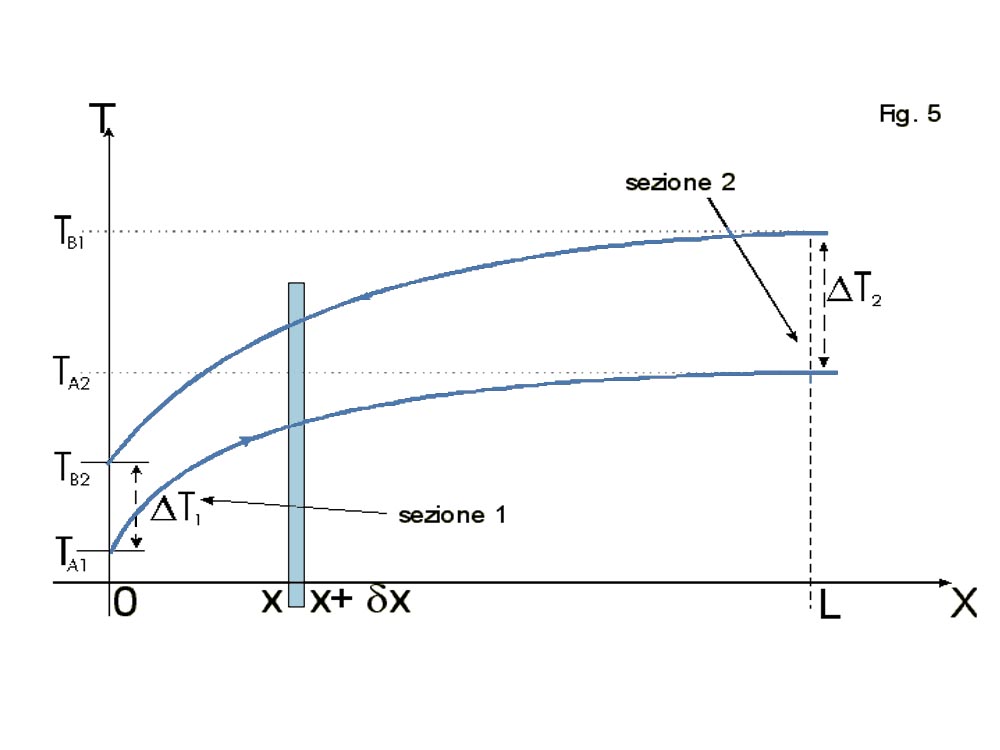
in cui notiamo che il ΔT rimane lungo tutto il tragitto, quasi costante, variando poco tra 0 ed L.
Passando al calcolo del ![]() , possiamo, date le considerazioni fatte, utilizzare l’espressione del
, possiamo, date le considerazioni fatte, utilizzare l’espressione del ![]() trovato in (18).
trovato in (18).
Negli scambiatori di calore in controcorrente, avremo, a parità delle quattro temperature di ingresso ed uscita dei due fluidi, un ![]() maggiore rispetto agli scambiatori di calore in equicorrente:
maggiore rispetto agli scambiatori di calore in equicorrente:
![]() (19)
(19)
Questo, dalla ![]() (K non è influenzato dalla corrente dei fluidi e
(K non è influenzato dalla corrente dei fluidi e ![]() ) si traduce nella minore necessità, da parte degli scambiatori in controcorrente, di superficie di scambio, e cioè è possibile costruire scambiatori meno ingombranti (e di conseguenza avere minori costi di materiale, dato che l’acciaio lucidato ha elevati costi).
) si traduce nella minore necessità, da parte degli scambiatori in controcorrente, di superficie di scambio, e cioè è possibile costruire scambiatori meno ingombranti (e di conseguenza avere minori costi di materiale, dato che l’acciaio lucidato ha elevati costi).
Si deve però considerare la bassa variazione di ΔT lungo il percorso: se da un punto di vista termodinamico questo potrebbe sembrare un vantaggio (poca perdita di energia), dal punto di vista dello scambio termico, questo significa avere uno scambio meno vivace, ovvero una maggiore lentezza nel cambiamento di temperatura del fluido di processo. Negli scambiatori in equicorrente, il forte ΔT iniziale, consente un brusco cambio di temperatura iniziale del fluido A, portandolo subito ad una temperatura più bassa [alta] in breve tempo.
In situazioni critiche (dove cioè si deve interrompere velocemente un processo termico, per es. per interrompere un processo di pastorizzazione) si useranno più scambiatori in serie: il primo sarà uno scambiatore in equicorrente per cambiare rapidamente la temperatura del fluido A, gli altri in controcorrente, in modo da ridurre spazio e quindi costi.
Esercizio sugli scambiatori di calore
Si deve raffreddare dell’azoto con dell’acqua, attraverso uno scambiatore di calore tubo in tubo.
L’azoto ha una portata ![]() e parte da una temperatura iniziale
e parte da una temperatura iniziale ![]() , per passare poi ad una temperatura di uscita pari a
, per passare poi ad una temperatura di uscita pari a ![]() .
.
L’acqua ha una portata ![]() e una temperatura iniziale
e una temperatura iniziale ![]() .
.
, calcolare la superficie di scambio S dello scambiatore, sia nel caso equicorrente, che nel caso controcorrente.
Lo scambiatore è dimensionato:
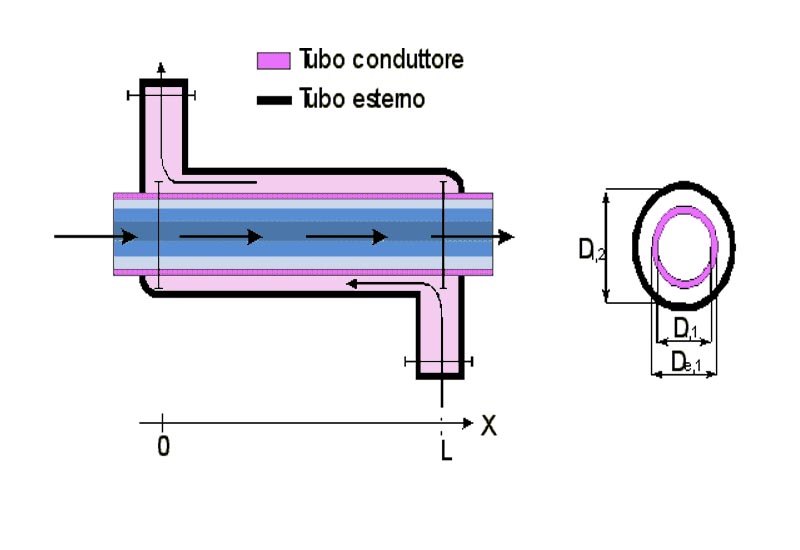
in cui: il diametro interno del tubo conduttore misura à Di,1 =101 mm
il diametro esterno del tubo conduttore misura à De,1=108 mm
il diametro interno del tubo esterno misura à Di,2 =125 mm
I° Punto:
La temperatura dell’acqua in uscita dal sistema può essere facilmente calcolata utilizzando le relazioni del bilancio di energia. Sappiamo infatti che la potenza termica dissipata dall’azoto, deve essere bilanciata da un assorbimento da parte dell’acqua di un’analoga quantità di energia:
![]()
e 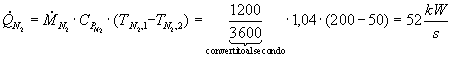
Sostituendo otteniamo: 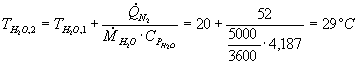
II° Punto:
Per la soluzione dovrò usare la relazione ![]() prima nel caso in equicorrente, e poi nel caso controcorrente. Calcoliamo i due
prima nel caso in equicorrente, e poi nel caso controcorrente. Calcoliamo i due ![]() e
e ![]() :
:
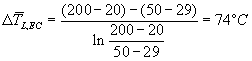
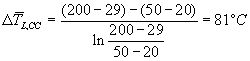
Per il calcolo del coefficiente di scambio :
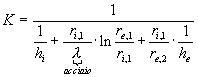
è necessario ricavare prima i coefficienti di convezione.
l’azoto entra ad una temperatura di 200°C ed esce a 50°C è consideriamo una temperatura media pari a 125°C=398K.
Poiché conosciamo il valore di pressione dell’azoto, dalla relazione dei gas perfetti, ricaviamo la densità:
![]()
grazie alla quale posso trovare la velocità alla parete:
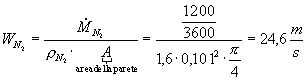
Posso quindi calcolare il n° di Reynolds:
![]()
dal cui valore sappiamo che l’azoto è in regime molto turbolento.
Per ricavare quindi il nostro coefficiente di convezione interna hi dobbiamo ricorrere al numero di Nüsselt secondo l'equazione di Dittus-Boelter che ha validità per i fluidi correnti in tubo in regime turbolento:
![]() è
è ![]()
dobbiamo ripetere le stesse operazioni, con la differenza che la densità dell’acqua, ritenuta incomprimibile, sarà ![]() e dovremo calcolare il diametro equivalente della corona circolare in cui scorre l’acqua.
e dovremo calcolare il diametro equivalente della corona circolare in cui scorre l’acqua.
![]()
![]()
Calcoliamo quindi la velocità dell’acqua:
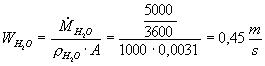
e quindi il n° di Reynolds:
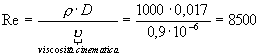
Poiché il n° di Reynolds è inferiore a 10000, non possiamo utilizzare le relazioni di Dittus e Boelter per trovare il n° di Nüsselt, ma dovrò usare la formula di Böhm:
![]()
Ottengo quindi un coefficiente di convezione ![]()
Posso calcolare il coefficiente di scambio, che risulta ![]()
Ricordando che la potenza scambiata era ![]()
Ottengo la superficie di scambio sia nel caso equicorrente che nel caso controcorrente.
![]()
![]()