Onde piane

Argomenti trattati:

Introduzione;

Onda piana progressiva;

Impedenza caratteristica di un mezzo;

Intensità acustica;

Onde piane non progressive;

Calcolo del coefficiente di assorbimento;

Densità di energia sonora;

Misura del coefficiente di assorbimento;

Prototipo di un tubo ad onde stazionarie.

Introduzione

La scienza che si occupa dello studio dei processi di generazione,propagazione e ricezione del suono,l’acustica,è fondata sui principi della teoria delle onde,in quanto queste ultime sono responsabili del fenomeno di trasporto dell’energia acustica.La relazione da cui si parte per lo studio delle onde è l’equazione di D’Alembert:

(1)

dove:

F è il potenziale della velocità;

c è la velocità di propagazione del suono.

Bisogna sottolineare che l’equazione di D’Alembert ,data la sua complessità,nella pratica si integra solo in tre casi:

1.onda piana progressiva;

2.onda sferica progressiva;

3.onda piana stazionaria.

In realtà esiste anche un quarto caso che è quello dell’onda cilindrica che trova riscontro in molte applicazioni pratiche ma,dato che presuppone una sorgente lineare anziché puntiforme,per la sua difficoltà non affrontiamo analiticamente.

1.Onda piana progressiva

Un onda piana progressiva è quell’onda che si sviluppa all’interno di un tubo di lunghezza indefinita, quando il fluido al suo interno viene sollecitato da un pistone che si muove con una legge del moto di tipo sinusoidale.Dato che l’onda si dice piana quando tutti i punti,rispetto a due delle tre coordinate cartesiane,si trovano nella medesima situazione,cioè in ogni istante hanno la stessa velocità e la stessa pressione,lo studio delle onde piane si affronta ricavando i campi di pressione p e velocità u.

p=p(x,y,z,t) u=u(x,y,z,t)

In più dal punto di vista spaziale è un problema di tipo monodimensionale perché la situazione geometrica in cui ci poniamo è un pistone piano infinito che si muove avanti e indietro lungo l’asse x(quindi dipende solo dalle variabili x e t ).Quindi si distingue un’onda piana per la configurazione geometrica della sorgente,piano indefinito che vibra nella sola direzione dell’asse x,e per la legge del moto di tipo sinusoidale da cui è regolata.

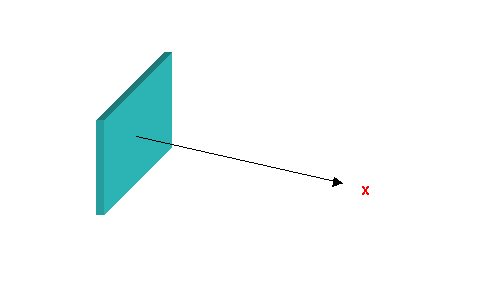
figura 1

Infatti la soluzione dell’equazione di D’Alembert per l’onda piana progressiva è di tipo armonico e si ricava grazie alle relazioni della velocità e della pressione in funzione del potenziale della velocità:

(1)

(2)

(al posto di u si può utilizzare anche in quanto la velocità è nel solo verso dell’asse x)

(3)

Prendendo come ipotesi di partenza il fatto che il campo scalare del potenziale della velocità sia eccitato in modo sinusoidale,sulla sorgente,che caratterizzo in x=0,il pistone sta vibrando eccitato dal seguente potenziale della velocità:

(4)

con chiamato numero d’onda.

(si utilizza convenzionalmente la funzione coseno perché quando si deriva questa espressione rispetto allo spazio o al tempo per ricavare rispettivamente velocità e pressione,si ottengono le suddette grandezze espresse con la funzione seno,che è il modo con cui generalmente si utilizzano)

Il potenziale della velocità si può anche esprimere in notazione complessa,detta anche di Eulero,per cui:

(5)

Generalmente si tende ad omettere la parte reale per comodità di scrittura ma la sua comprensione è importante in quanto,essendo il potenziale della velocità una grandezza reale,solo la parte reale ha significato fisico!

Da queste prime considerazioni si deduce che il problema dell’onda piana progressiva è di tipo lineare,perché lineare la sua equazione del moto;di conseguenza se si eccita il sistema con una frequenza w ,per la proprietà di linearità,esso risponderà con la stessa frequenza w.Un esempio di sistema completamente lineare è il campo acustico in sé;sono i trasduttori elettro-meccanici o meccano-acustici,dispositivi che trasformano una grandezza fisica,in questo caso acustica,in un’altra(ad esempio elettrica),che sovente non sono perfettamente lineari provocando il fenomeno della distorsione armonica.

Questo grosso difetto che accompagna gran parte dei trasduttori è responsabile della mancata capacità di mantenere inalterata la forma d’onda del segnale d’entrata,in uscita e si verifica negli altoparlanti. L’altoparlante è un apparecchio utilizzato per trasformare l’energia di un segnale elettrico in energia acustica irradiata nell’ambiente circostante.Teoricamente si vorrebbe che il segnale d’uscita avesse lo stesso contenuto in frequenza del segnale elettrico d’entrata ma,a causa della distorsione armonica,il segnale d’uscita ha frequenze multiple della frequenza fondamentale.

Esempio:Se introduco nell’altoparlante una frequenza di 500 Hz ,in uscita avrò una componente armonica a 1000 Hz,una a 1500 Hz,una a 2000 Hz.Ognuna di queste ha una sua ampiezza e fase ,rispetto alla fondamentale,che non sempre sono descrivibili in maniera semplice dal punto di vista matematico.

figura 2

Viceversa,il problema della distorsione armonica diventa un pregio per quanto riguarda il campo degli strumenti musicali perché permette ad uno strumento di irraggiare nell’ambiente esterno frequenze con uno spettro molto vasto.Il violino è un trasduttore meccano-acustico fortemente non lineare che è valutato dal punto di vista economico proprio in base alla intrinseca distorsione armonica che riesce a introdurre.

Proprio per il fatto che nell’aria,se la legge del moto della superficie vibrante è armonica,la propagazione dell’onda segue totalmente la funzione cosinusoidale,si ha che tutti i punti del campo seguono pedissequamente il punto dove il campo è stato generato facendo coincidere la soluzione dell’equazione di D’Alembert con la stessa condizione al contorno iniziale per cui:

in x=0 (6)

Ora che è stata verificata la legge del moto dell’onda piana progressiva si possono ricavare la velocità e la pressione.Per la particolare situazione geometrica scelta,il gradiente si riduce alla sola derivata direzionale lungo x:

(7)

Il valore –j indica che la velocità è sfasata di -p/2 rispetto al potenziale e quindi quest’ultimo è una grandezza cosinusoidale,mentre la velocità è sinusoidale.Per ricavare la costante Fmax impongo la condizione all’origine,in cui il pistone nella posizione centrale dell’oscillazione x=0 e all’istante iniziale di osservazione del fenomeno t=0 ,presenta velocità massima:

(8)

(9)

Si conclude che:

(10)

da cui:

(11)

Analogamente si procede per il calcolo della pressione (3) :

(12)

(13)

(14)

da cui

(15)

Impedenza caratteristica di un mezzo

Disponendo di pressione e velocità,si può calcolare un’altra grandezza importante denominata impropriamente:impedenza caratteristica del mezzo z (impropriamente perché è caratteristica solo delle onde piane progressive che in natura non esistono!)L’impedenza è il rapporto tra i moduli di pressione e velocità.Essa è una funzione reale in quanto rapporto tra due funzioni sinusoidali in fase tra loro(ricorda:solo per l’onda piana progressiva sono in fase u e p!)Quindi sostituendo a p e a u le corrispettive espressioni si ricava che:

(16)

L’unità di misura dell’impedenza è:

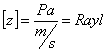(17)

Fisicamente l’impedenza acustica valuta quanto un campo è “morbido” cioè in che modo reagisce alla sollecitazione di una forza quale può essere quella di pressione del suono.Questa relazione è quindi interessante poiché fornisce un legame quantitativo tra pressione e velocità; dimostra che in un campo acustico a bassa impedenza,con poca pressione, si riescono ad ottenere velocità notevoli mentre se il campo è ad alta impedenza servono pressioni elevate per ottenere velocità apprezzabili.Di nuovo,per avere riscontro con la realtà,si può citare l’esempio degli altoparlanti,il cui scopo è generare,sollecitati da una velocità impressa elettricamente,una pressione che verrà poi percepita dal nostro orecchio.

Il principio di funzionamento dell’altoparlante a tromba (figura 3)tiene conto proprio della relazione quantitativa tra pressione e velocità e infatti il campo più consono per un buon funzionamento è quello con impedenza alta e velocità basse,quindi con poca energia meccanica sull’altoparlante:in questo modo si ottengono pressioni elevate.

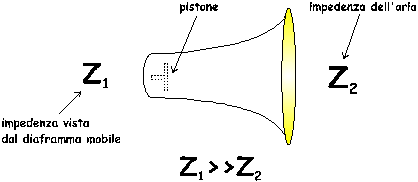
figura 3

Il diaframma mobile in prossimità dell’imboccatura della tromba vede un’impedenza Z1 molto maggiore di quella dell’aria Z2 all’altra estremità.

L’impedenza per l’onda piana progressiva risulta essere costante:

(18)

Intensità acustica

Un altra grandezza che è interessante calcolare per valutare il fenomeno del trasporto di energia dell’onda piana progressiva è l’intensità acustica che rappresenta il valore medio nel tempo dell’intensità istantanea Ii(t)

(19)

da cui l’intensità media

(20)

Dopo aver riscritto le equazioni della velocità e della pressione in funzione dell’impedenza:

(21)

(22)

posso calcolare l’intensità media (ricordando la formula trigonometrica :

(23)

la quale vale ½ se integrata mediamente nel tempo ) ottenendo tre possibili risultati:

(24)

(25)

(26)

Se poi si utilizzano le espressioni dei valori medi efficaci ,in quanto si parla di grandezze sinusoidali, e (l’acronimo rms sta per Root Mean Square):

(27)

(28)

l’intensità può essere riscritta come:

(29)

(30)

(31)

In generale c’è la tendenza ad abusare di queste formule per la loro estrema comodità di calcolo e semplicità,soprattutto per quanto riguarda la (30).Infatti fino agli anni Ottanta questa espressione era usata per calcolare l’intensità di qualsiasi forma d’onda,commettendo un grossolano errore dal momento che recentemente si è appurato che vale solo per l’onda piana progressiva!Ciò che aveva tratto in inganno era il significato fisico di equivalente energetico del valor medio efficace.Si indicava con esso ,sbagliando, l’energia immagazzinata dal sistema invece di far riferimento solo all’energia potenziale.Avendo calcolato solo il valor medio efficace della pressione in un campo acustico generico,non si è in grado di valutare l’energia cinetica in quanto non è detto che tutta l’energia potenziale si trasformi in energia cinetica!Anzi solitamente l’energia immagazzinata come energia potenziale è mediamente maggiore dell’energia cinetica e viceversa ci sono casi in cui è vero il contrario ,cioè che l’energia immagazzinata in termini di velocità,e quindi l’energia cinetica, è superiore all’energia potenziale.Solo per l’onda piana progressiva sussiste la seguente uguaglianza:

(32)

e dall’uguaglianza dell’intensità si scrive:

(33)

Quindi nell’apprestarsi allo studio di un onda qualsiasi non è sufficiente conoscere solo la pressione per valutare l’intensità,occorrono pressione e velocità. L’unico termine che rimane sempre valido è l’intensità valutata come media integrale nel tempo.

Onde piane non progressive

Nel caso di apprestarsi allo studio di un generico sistema sinusoidale di onde piane non perfettamente progressive (potrebbe essere il caso di un’onda che si riflette parzialmente)si utilizzano le equazioni valide per l’onda piana progressiva col solo accorgimento di introdurre il termine che riguarda la fase j,perché p e u non sono più in fase.

Dato che normalmente il sistema viene eccitato imponendogli una certa velocità,l’espressione di u è presa come riferimento per il calcolo della pressione nella quale è presente la fase (vedi notazione complessa).

(34)

(35)

Si può quindi ricavare l’impedenza:

(36)

che in modulo è uguale a quella dell’onda piana progressiva mentre ha una fase ruotata di j .

Quando poi si calcola l’intensità

(37)

compare il termine cosj dovuto allo sfasamento tra p e u che riduce il valore dell’intensità trasportata dall’onda.

j =0 è il caso dell’onda piana progressiva;

j =90 è il caso dell’onda piana stazionaria(onda generata da un pistone che comprime il fluido in un tubo di lunghezza finita)per cui l’intensità è nulla.

Calcolo del coefficiente di assorbimento

Si può anche considerare il caso di un onda piana non progressiva all’interno di un sistema intubato(si prende questo riferimento perché abitualmente si studia il comportamento delle onde nel “tubo di Kundt”,figura 4)di lunghezza finita:ad un’estremità del tubo c’è il pistone,o l’altoparlante,che vibra lungo l’asse x allo scopo di generare un treno di onde piane;all’altra un tappo di materiale con caratteristiche meccaniche(velocità di propagazione d’onda,impedenza caratteristica del mezzo,densità,..)diverse da quelle dell’aria,di cui si vuole calcolare l’impedenza e il coefficiente di assorbimento acustico.Suppongo che il materiale abbia una propria impedenza .

(38)

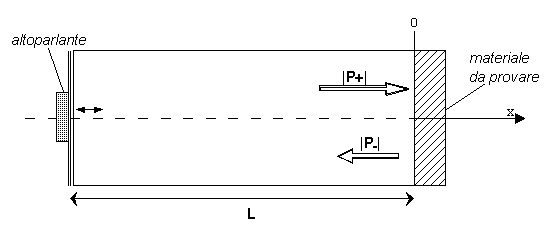
figura 4

La pelle del materiale reagisce ad un’onda elastica in modo diverso dall’onda piana progressiva;se il materiale presenta impedenza infinita l’onda riflessa ha intensità uguale a quella dell’onda incidente e le due onde si compensano;se l’impedenza è 0<z<¥, l’onda progressiva si scontra contro la superficie di destra e torna indietro incontrando le nuove onde che arrivano, generando all’interno del tubo un sistema di energie:una quota di solito considerevole fluisce da sinistra a destra(quella propria dell’onda progressiva),l’altra da destra a sinistra(nella realtà è notevolmente minore della prima).Se si analizza il sistema dal punto di vista energetico,supponendo valido il principio di sovrapponibilità degli effetti,si identifica un’intensità incidente ,calcolabile come se ci fosse solo il campo incidente,che incontra l’interfaccia aria-solido,e un’intensità riflessa .Dal punto di vista fisico esiste un’altra quota di energia,quella assorbita , in quanto l’intensità di un’onda che si scontra su una superficie in parte viene assorbita e in parte riflessa.

In formule :

(39)

Dividendo entrambi i membri della (39) per ottengo dei rapporti che prendono il nome di coefficiente di assorbimento a e coefficiente di riflessione r.

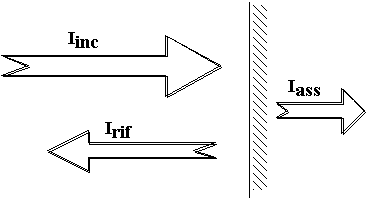
figura 5

(40)

(41)

(Entrambi ovviamente sono in modulo minori di 1 perché la loro somma deve restituire l’unità)

Si può anche considerare il caso di una doppia interfaccia solido-aria su cui incide un’onda sonora(figura 6).In questa situazione l’intensità trasportata dall’onda,intensità incidente ,si divide in tre quote:

l’intensità riflessa ,che torna nell’aria e dipende dall’angolo di incidenza,dalla frequenza,dalla differenza di impedenza tra l’aria e il materiale che costituisce la parete;

l’intensità assorbita ,che è la quota intrappolata all’interno del materiale e dissipata in calore(quota d’energia effettivamente assorbita);

l’intensità trasmessa ,che è quella che attraversa il solido e entra nell’ambiente adiacente.

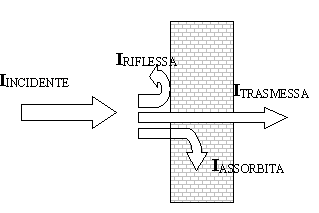
figura 6

Quindi come prima:

(42)

E dividendo per :

(43)

(44)

Dove r è il coefficiente di riflessione,a quello di assorbimento,t di trasmissione.

Ciò che interessa realmente non è a ma la quota che si vede riflessa dietro la parete:

(45)

a prende il nome di coefficiente di assorbimento acustico apparente (apparente perché quello “vero”è a ) che è la grandezza che quantifica la predisposizione che una superficie ha ad assorbire il suono.

Se a =0 , la superficie è completamente riflettente;

se a =1 , la superficie è totalmente assorbente.

Una finestra aperta è una buona superficie assorbente per un osservatore posto nell’ambiente che produce il suono (a grande).

( in realtà essa trasmette tutta l’intensità che riceve verso l’esterno;per questo si parla di a come di coefficiente acustico apparente)

I materiali che si considerano buoni assorbenti(detti anche materiali fonoassorbenti) normalmente presentano determinate caratteristiche,sono cioè leggeri,morbidi,con un’impedenza simile a quella dell’aria(ricorda:il massimo assorbimento si ha quando l’impedenza dei due materiali è uguale);al contrario i materiali utilizzati per l’isolamento acustico sono duri e pesanti in modo che le onde sonore non riescano a deformarli. L’isolamento acustico presenta necessità differenti rispetto all’isolamento termico infatti un ottimo isolante termico come il polistirolo è un pessimo isolante acustico in quanto si comporta da amplificatore del suono.

L’altra caratteristica importante che deve avere un materiale di natura fibrosa o cellulare,per essere un buon assorbente, è di essere a strutture aperte;per questo bisogna fare attenzione a non otturare i pori superficiali quando si ricopre un materiale assorbente con vernici o pitture .Infatti se il suono incide sul materiale a celle aperte(esempi di materiali porosi sono lana,vetro,isolanti di schiuma,..) ,esso penetra nei pori e nei canalicoli esistenti ponendo in vibrazione le molecole d’aria presenti negli interstizi.Tali oscillazioni all’interno delle cellule,per effetto combinato della viscosità dell’aria e della sua aderenza alle pareti,dissipano energia sotto forma di attrito. A questi fenomeni di carattere meccanico,si accompagnano fenomeni di dissipazione termica per effetto delle successive compressioni e decompressioni dell’aria provocando l’assorbimento del suono. Tuttavia,l’assorbimento sarà tanto maggiore quanto maggiore sarà la velocità del moto oscillatorio trasmesso alle molecole d’aria.

Tale velocità,nulla quando l’onda sonora arriva a incidere sulla parete rigida sulla quale è applicato lo strato poroso,ha valore apprezzabile solo se lo spessore dello strato è sufficientemente grande e di un ordine di grandezza paragonabile alla lunghezza d’onda del suono incidente.Quindi con gli spessori abituali di qualche centimetro,il valore del coefficiente di assorbimento si mantiene elevato e costante per frequenze superiori a 1000 Hz. Infatti il coefficiente si mantiene costante solo per quella banda di frequenze che superano un valore limite inferiore,valutabile come quello per cui lo spessore s risulta pari a ¼ della lunghezza d’onda l corrispondente alla frequenza in questione.Ecco perché spesso conviene applicare lo strato poroso a una distanza dalla parete uguale a ¼ della lunghezza d’onda incidente,dove la velocità di vibrazione dell’onda acustica presenta il suo massimo.

La relazione che mostra come varia lo spessore del materiale in funzione della lunghezza d’onda è:

(46)

Un altro esempio di buon assorbente è il pannello vibrante che si presta bene ad assorbire le basse frequenze:esso consiste in una lastra di forma regolare,montata a distanza opportuna dalla parete rigida ,dove,se lo spessore dell’intercapedine è piccolo e il materiale del pannello sufficientemente cedevole,il comportamento del sistema pannello - aria - parete è assimilabile al moto armonico di una massa vibrante M (il pannello) collegata con un vincolo elastico (aria contenuta nella parete),di caratteristica intrinseca k, a un sostegno rigido(parete).La frequenza propria di vibrazione del sistema meccanico è data da:

(47)

In più per allargare la banda di frequenze per la quale si ha un buon assorbimento ,si può applicare al pannello uno strato poroso,in modo da accoppiare all’effetto della risonanza quello della porosità.

Densità di energia sonora

La densità di energia sonora D rappresenta la quantità di energia contenuta nell’unità di volume o,meglio,la quantità di energia per metro cubo:

(48)

Essa si misura:

(49)

Sapendo che l’intensità è un vettore che rappresenta l’energia trasportata nell’unità di tempo attraverso l’unità di superficie,se si considera il caso di un’onda piana progressiva entrante in una superficie di sezione ,immaginando di lasciar fluire l’onda attraverso questa superficie per un secondo,essa invaderà un volume di forma prismatica e di valore ,dove c è la velocità del suono.

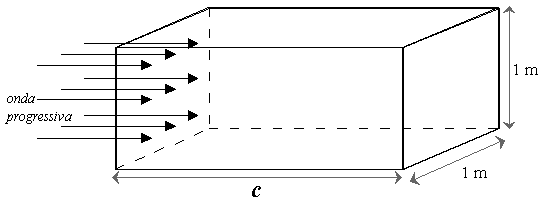
figura 7

L’energia che è entrata nel prisma si può scrivere come: ,dove S rappresenta la sezione del prisma,per quello in questione unitaria,e I,l’intensità.Quindi si può ricavare la relazione fondamentale per la densità(di nuovo valida solo per l’onda piana progressiva):

(50)

Ora siccome si può considerare la densità totale come la somma della densità che si sta propagando e la densità che continua a oscillare avanti e indietro:

(51)

(per l’onda piana progressiva e )

si può cercare di determinare il coefficiente di assorbimento di un materiale sfruttando questa nuova grandezza.

Partendo dal fatto che l’ipotesi di sovrapponibilità degli effetti sia sempre valida,si può distinguere l’intensità totale nelle componenti riflessa e incidente:

(52)

e, presa singolarmente ,ciascuna di queste componenti rappresenta l’intensità di un onda piana progressiva per cui vale l’equazione (50).Da ciò,sfruttando nuovamente il principio di sovrapponibilità degli effetti,si può esprimere la densità di energia totale nel tubo come:

(53)

Quindi se tramite un intensimetro , strumento capace di misurare l’intensità,si misurano l’intensità e la densità di energia,disponendo delle seguenti relazioni, si può calcolare il coefficiente di assorbimento a:

(54)

(55)

(56)

Eseguendo le opportune sostituzioni si ricava:

(57)

che rappresenta una stima del coefficiente di assorbimento del materiale all’estremità del tubo.

Per misurare l’intensità servono pressione e velocità;se si pongono due microfoni a breve distanza tra loro è possibile ricavare l’intensità come media nel tempo dell’intensità istantanea.Ricordando che:

(58)

(59)

E sapendo che per l’onda piana progressiva queste due espressioni coincidono,e quindi è indifferente parlare di energia cinetica o potenziale, si possono introdurre i termini di intensità cinetica e potenziale:

(60)

dove è la densità di energia cinetica;

(61)

dove è la densità di energia potenziale.

Analiticamente descrivere l’intensità in questo modo è corretto mentre dal punto di vista fisico non è vero che localmente l’energia è ripartita equamente in potenziale e cinetica,è vero globalmente poiché mediamente nel tempo e nello spazio l’energia sarà metà cinetica e metà potenziale(in quanto oscilla tra l’una e l’altra condizione).Quindi il procedimento corretto è combinare le ultime due espressioni nella nuova:

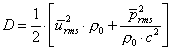(62)

la quale è vera sempre,cioè non dipende dal campo sonoro che si sta considerando;è dimostrato anche dal fatto che il primo principio della termodinamica,riguardante la conservazione dell’energia,deve essere sempre rispettato.

OSSERVAZIONI:

In generale per avere una caratterizzazione completa del campo si deve disporre di due tipi di grandezze:

GRANDEZZE DI CAMPO = pressione,velocità

GRANDEZZE ENERGETICHE = intensità,densità

Esse sono omogenee tra loro ma non tra i due gruppi(pressione e velocità sono omogenee,pressione e densità sono disomogenee).Per questo motivo è errato pretendere di calcolare il rapporto tra intensità e pressione(permesso solo nel caso dell’onda piana progressiva)!Il risultato a cui si arriverebbe è un numero indefinito in quanto si effettua il rapporto tra una grandezza intensimetrica ,e quindi vettoriale, e una grandezza scalare.Bisogna fare molta attenzione perché questo problema è stato fonte di numerosi errori in passato.Solo recentemente,anni Novanta,l’ente normativo sopranazionale ISO (International Standard Organization) ha provveduto ad emettere delle norme tecniche in riguardo!

Misura del coefficiente di assorbimento

Una delle tecniche più utilizzate per la misura ,dal punto di vista pratico, del coefficiente di assorbimento è l’introduzione nel tubo,dove scorrono le onde, di un microfono;esso è libero di scorrere lungo l’asse del tubo stesso.Se si riporta in un diagramma il valore complessivo della pressione totale misurata dal microfono nei punti compresi tra –L e 0 si trova un andamento simile a quello del grafico sottostante nel quale si può individuare la presenza di massimi e minimi (la pressione sulla parete raggiunge di solito un valore prossimo a quello massimo).

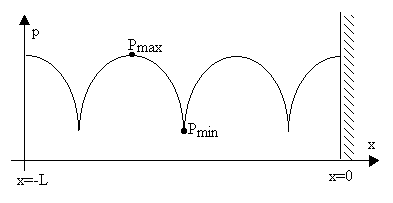
figura 8

I valori che interessano sono i massimi e i minimi che si individuano quando onda incidente e onda riflessa sono rispettivamente in fase o controfase.Per questo metodo è quindi necessario lo studio e la ricerca dei massimi e minimi che possono essere assai laboriosi!Si ovvia a questo problema studiando la pressione incidente e la pressione riflessa, ricavate sempre sperimentalmente con l’utilizzo del microfono suddetto. Questa relazione in termini analitici assume la forma:

(63)

(64)

Risolvendo il sistema si ottiene:

(65)

(66)

Da cui si ricava abbastanza velocemente il coefficiente di assorbimento a:

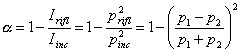(67)

Prototipo di un tubo ad onde stazionarie

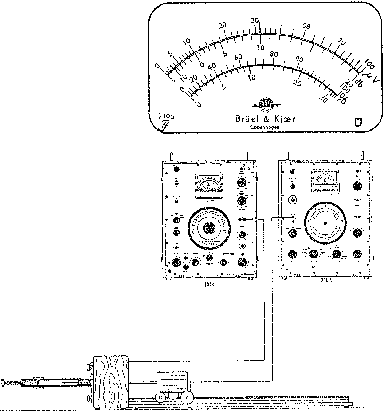
Il tubo ad onde stazionarie,o “tubo di Kundt” è un tubo di lunghezza finita con un pistone ad una estremità e all’altra un “tappo”di un certo materiale di cui si vogliono calcolare l’impedenza e il coefficiente di assorbimento.Nella figura sottostante(figura 9) è rappresentata la versione commercializzata dalla ditta Bruel&Kjaer di Copenaghen del “tubo di Kundt”:

Figura 9

Si possono adoperare due tubi permutabili: uno dal diametro di circa 100mm e lungo circa 1,5m e un altro (che si vede montato sopra l’altoparlante) che ha un diametro di 29mm ed è lungo circa 0,5m. All’estremità si collocano i portaprovini (gli anelli di acciaio che si intravedono in alto a destra), all’interno dei quali si mette il materiale da provare (intonaco, gommapiuma).

Il tubo viene quindi montato sul perno di legno di forma rettangolare (che contiene un altoparlante) e il microfono è quel cilindro orizzontale che si muove su un carrellino e prende il segnale attraverso un tubicino (il “microphone probe” indicato nel sottostante Schema 1) che scorre dentro al tubo centrale e fa da trasduttore di pressione lungo l’asse. Sulla base del supporto per il microfono c’è una stecca graduata con un cursore che consente di misurare con la precisione di 1/10mm le distanze dal provino.

Segue uno schema di principio del tubo di Kundt:

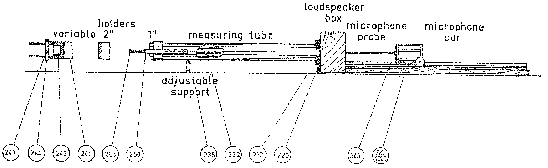
Schema 1

Nello schema funzionale(schema 2) che segue

Schema 2

è rappresentato il classico uso del tubo: per compiere le misure è necessario un generatore di segnale sinusoidale da applicare all’altoparlante e i valori del rapporto si misurano grazie alla lettura sul voltmetro dei valori di tensione (in , su una scala di precisione) provenienti dal microfono e si può così desumere il coefficiente di assorbimento grazie ai valori tabulati sul diagramma seguente che rappresenta il coefficiente di assorbimento a in funzione del rapporto .

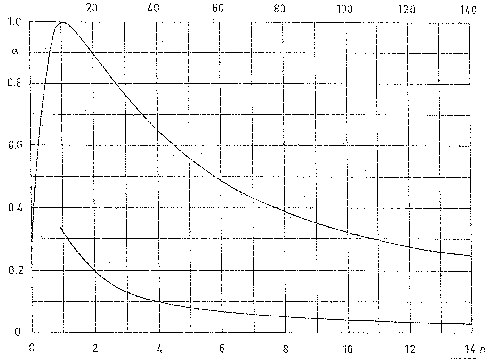
figura 10

Nonostante ciò,il tubo di Kundt è uno strumento ormai caduto in disuso, per una serie di motivi:

- le misure sono lente: bisogna eseguirne una per ogni singola frequenza (per ricavare , cioè vedere come varia l’assorbimento del materiale in funzione della frequenza)

- la misura dentro un tubo su un piccolo campione può non essere rappresentativa del comportamento del materiale in esame su grande superfici.

Esistono tecniche più moderne che si basano su misure in banda larga: anziché generare un suono puro a una singola frequenza, si produce un segnale che copre una vasta zona dello spettro di frequenze; utilizzando teorie complesse di analisi dei segnali, si ricava direttamente lo spettro di assorbimento. Recentemente sono state sviluppate ulteriori tecniche di misura basate sull’intensimetria, che non richiedono l’ipotesi di onde piane e che quindi si possono compiere anche al di fuori del tubo. Il tubo ad onde stazionarie rimane tuttavia un utile modello didattico.