Francesco Garaffa, n.matricola 124011
lezione del 17/10/00, ore 14:30-16:30

Miscele di gas perfetti

Legge di Dalton

La legge di Dalton afferma che una miscela di gas perfetti ha una pressione p_tot che si può esprimere come somma delle pressioni parziali p_i dei singoli componenti.

La pressione parziale p_i rappresenta la pressione esercitata dal gas i-esimo occupante tutto il volume V disponibile in assenza degli altri componenti.

Supponiamo quindi che in un contenitore di volume V si trovino alla temperatura T, un numero N di gas perfetti. Indicando con 1,2, …,n i gas si ottiene:

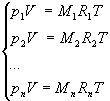
in cui p_i rappresenta la pressione parziale dell’i-esimo gas.

Essendo per la legge di Dalton:

si ottiene quindi, sommando membro a membro le equazioni del sistema:

Essendo poi evidentemente:

si può calcolare la costante R_tot della miscela:

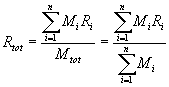
che rappresenta la media pesata degli R dei componenti.

La legge di Dalton afferma in pratica che ad una qualsiasi miscela composta da due o più gas perfetti è possibile applicare il principio della sovrapposizione degli effetti.

Utilizzando l’equazione di stato nella formulazione:

in cui n rappresenta il numero di moli, con un analogo procedimento si giunge a:

ma:

è il numero di moli totali della miscela. In questo caso:

Riassumendo, per un gas componente una miscela si può scrivere:

mentre per la miscela stessa:

Eseguendo il rapporto membro a membro si può calcolare la frazione molare dell’i-esimo componente o percentuale in volume x_i :

Analogamente definiamo la frazione massica G_i come il rapporto:

Esempio 1 – Scatolone adiabatico

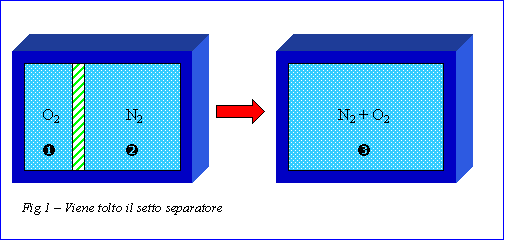
Si dispone di un recipiente termicamente isolato, separato al suo interno da un setto rigido che lo divide in due parti: la prima contiene ossigeno, la seconda azoto (fig.1). Si vogliono calcolare le coordinate termodinamiche dello stato finale raggiunto togliendo bruscamente il setto separatore. Inoltre si vuole stimare l’eventuale aumento di entropia.

DATI
P1 = 1 BAR	V1 = 1 m^3	T1 = 100°C
P2 = 2 BAR	V2 = 2 m^3	T2 = 100°C

Risoluzione

Consideriamo il miscuglio finale come un gas perfetto. Ricaviamo la massa dell’ossigeno e dell’azoto dall’equazione di stato per la situazione 1 e 2:

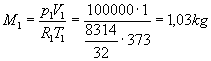
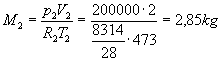
Scriviamo l’equazione di stato per la situazione 3:

in cui R₃ rappresenta la media ponderata degli R dei componenti cioè:

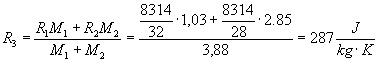
analogamente per c_v e per c_p:

Siccome il sistema è chiuso e il processo è adiabatico, sia la massa che l’energia si conservano nella trasformazione, cioè:

e

Essendo:

risulta:

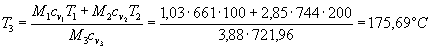
E’ semplice ora calcolare p₃:

E’ possibile calcolare le percentuali in massa del Nitrox (miscela di ossigeno e azoto) ottenuto nella trasformazione:

-percentuale in massa dell’ossigeno:

-percentuale in massa dell’azoto:

Più comunemente però, si utilizzano le percentuali molari:

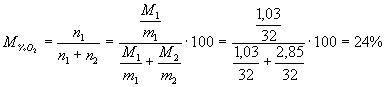
quindi evidentemente:

.

Osserviamo che l’aria pura è composta dal 21% di ossigeno e dal 79% di azoto.

Calcoliamo infine la variazione di entropia verificatasi nella trasformazione; essa è diversa da zero in quanto il processo è evidentemente irreversibile. Per aiutarci nel calcolo possiamo applicare il principio di sovrapposizione degli effetti: immaginiamo quindi che ciascuno dei due gas si sia espanso nel vuoto, calcoliamo la variazione di entropia in entrambe le trasformazioni e infine sommiamo le due variazioni.

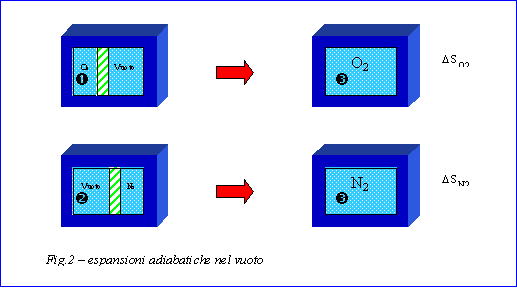
Il gas espandendosi nel vuoto compie una trasformazione isotermica.

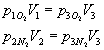
ricavo quindi le pressioni dell’ossigeno e dell’azoto nella situazione 3:

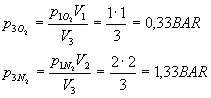
Ora, applicando la formula della variazione di entropia per le trasformazioni isotermiche:

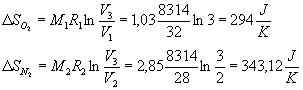
La variazione totale di entropia è quindi la somma delle variazioni parziali:

Esempio 2 – Pompa da bicicletta

Si considera una pompa da bicicletta inizialmente nella posizione rappresentata dalla fig.3a. L’interno della pompa è a pressione atmosferica p_i e la temperatura iniziale è T_i. Si imprime quindi una forza allo stantuffo in modo che tutta l’aria contenuta nella pompa risulta essere compressa nella camera d’aria (fig.3b). Ipotizzando che il processo si verifichi in condizioni quasi-statiche e sia adiabatico, si calcolino le coordinate termodinamiche dello stato finale e il lavoro netto compiuto sul sistema. Inoltre si dica se la trasformazione comporta un aumento di entropia.

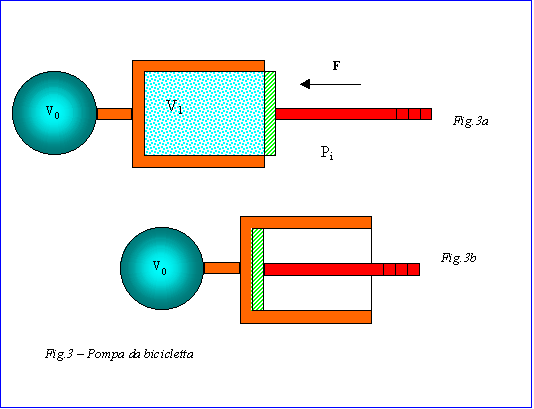
DATI
Pi = 1 BAR	V0 = 1 m^3	V1 = 2 m^3	Ti = 20°C

Risoluzione

Il grafico pV del processo è il seguente:

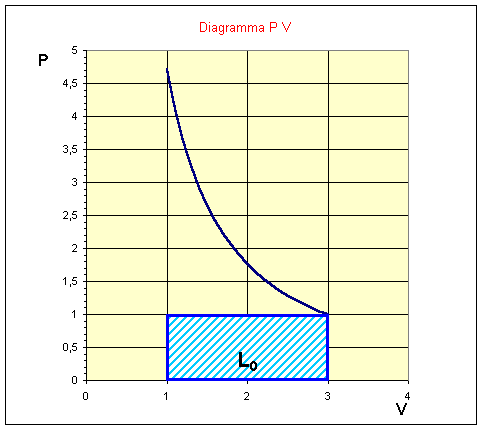
L’approccio del problema porta a considerare il sistema costituito dalla pompa e dalla camera d’aria come un sistema chiuso. Notiamo innanzitutto che il volume iniziale è dato dalla somma del volume della pompa e del volume della camera d’aria.

Inoltre essendo la trasformazione un’ adiabatica reversibile, la relazione tra p e V è data da:

in cui:

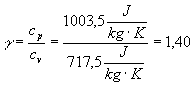
nel caso dell’aria (per i valori dei coefficienti specifici vedi tabella finale).

Quindi per la trasformazione sopra si può scrivere:

quindi numericamente:

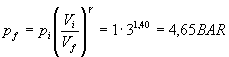
Usando l’equazione di stato nello stato iniziale:

si può ricavare la massa dell’aria contenuta nel sistema:

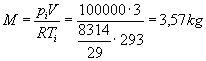
A questo punto per trovare il lavoro, usando il primo principio della termodinamica:

e ricordando che la trasformazione è adiabatica:

posso calcolare il lavoro:

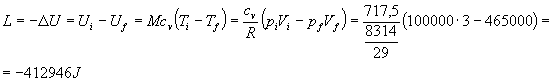
Allo stesso risultato si poteva pervenire tramite il calcolo di un integrale. Essendo infatti:

utilizzando l’espressione della trasformazione adiabatica:

si ottiene:

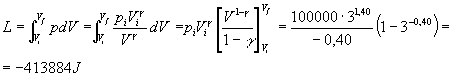
E’ evidente che a tale lavoro andrà sottratto il lavoro svolto dalla pressione atmosferica (rappresentato dall’area tratteggiata nel grafico sopra), per calcolare il lavoro netto svolto sul sistema:

Il processo non ha causato un aumento di entropia dell’universo, infatti:

ma essendo la trasformazione un’adiabatica reversibile:

e quindi:

Esercizio A – Efflusso da un ugello

Supponiamo di avere una bombola di volume V₁ contenente un gas alla pressione p₁. Immaginando di aprire all’improvviso il rubinetto di questa bombola, si osserverà una forte fuoriuscita del gas dall’ugello. Si vuole calcolare la velocità media w₂ del gas uscente.

---

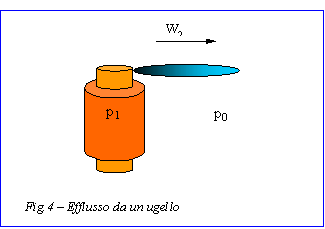
Risoluzione

Osserviamo innanzitutto che la velocità di uscita non dipende dalla sezione del foro.

Per la risoluzione di questo problema è necessario inoltre considerare soddisfatte le seguenti approssimazioni:

1. il processo può essere considerato adiabatico reversibile, possono cioè essere trascurate tutte le dissipazioni di energia verso l’esterno;

2. l’energia cinetica nello stato iniziale può essere ritenuta nulla, essendo trascurabile rispetto all’energia cinetica nello stato finale.

Consideriamo l’energia totale formata dal contributo dell’energia cinetica e

dell’energia interna:

Si verifica, tramite considerazioni microscopiche dei fenomeni che avvengono nell’ugello che il lavoro svolto dal sistema verso l’esterno vale:

quindi per il primo principio della termodinamica:

Ricordando che:

si ha:

Essendo inoltre:

si ottiene l’equazione risolutrice del problema:

E’ noto che nelle trasformazioni adiabatiche vale la relazione:

cioè:

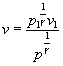
risolvendo l’integrale:

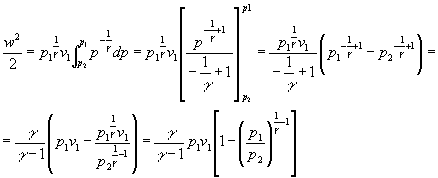
in definitiva la velocità media vale:

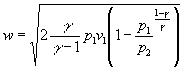
Esercizio B – Sollevamento di un grave

Si considera un recipiente contenente un gas a una data pressione p₁ avente la parte superiore mobile, sulla quale è appoggiato un grave di massa M. Supponendo di comunicare al gas un calore Q, il gas subirà una trasformazione isobara. Si vuole calcolare il lavoro netto svolto dal sistema e il volume finale.

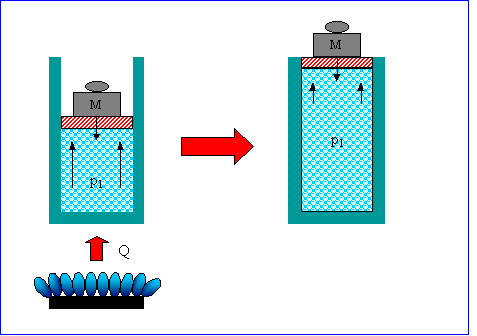
Risoluzione

Dal primo principio in forma entalpica si ha:

ma essendo la trasformazione isobara:

integrando dallo stato iniziale a quello finale:

quindi la temperatura finale è data da:

Applicando ora l’equazione di stato:

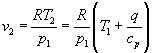
Vediamo ora il grafico pv della trasformazione:

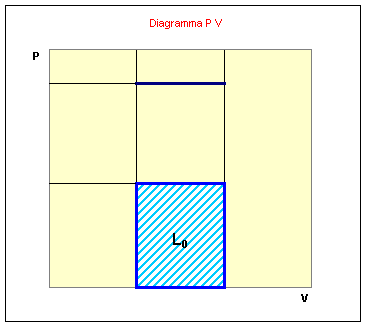
Calcoliamo ora il lavoro svolto dal sistema sull’ambiente. Siccome:

si ottiene osservando il grafico:

ora bisogna sottrarre a questo lavoro il lavoro svolto dall’ambiente l₀:

in cui p₀ è la somma della pressione atmosferica e della pressione esercitata dal grave sul recipiente.

Esercizio C – Compressioni adiabatiche e isotermiche

Richiamando l’esercizio 2, supponiamo di avere due pompe da bicicletta differenti: la prima effettua una compressione adiabatica, la seconda una compressione isotermica. Entrambe le pompe agiscono nelle stesse condizioni di pressione iniziale e finale. Si vuole stabilire quale delle due trasformazioni comporta il minor lavoro esterno.

Risoluzione

Osserviamo il grafico delle due trasformazioni:

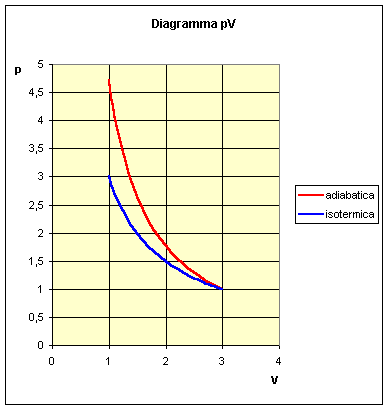
Già dal grafico si può intuire che il lavoro minore compete alla trasformazione isotermica. Sappiamo che per una trasformazione isotermica vale la relazione:

Ricaviamo quindi il lavoro in tale trasformazione:

Per la trasformazione adiabatica invece, vale la relazione:

e il lavoro corrispondente vale:

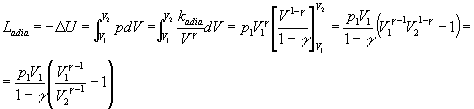
Verifichiamo ora quanto osservato nel grafico, tenendo presente che i lavori sopra calcolati sono negativi:

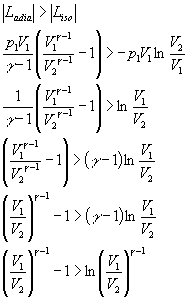
Ponendo ora:

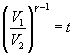
si ottiene:

disuguaglianza verificata per ogni valore di t.

Tabella A – Proprietà di alcuni gas perfetti (a 300 K)

Gas	Massa molecolare [kg/kmol]	R [J/kgK]	Cp [J/kgK]	Cv [J/kgK]
Aria	28,97	287,00	1003,5	716,5	1,400
Argon	39,948	208,13	520,3	312,2	1,667
Butano	58,124	143,04	1716,4	1573,4	1,091
Anidride carbonica	44,01	188,92	841,8	652,9	1,289
Monossido di carbonio	28,01	296,83	1041,3	744,5	1,400
Etano	30,07	276,50	1766,2	1489,7	1,186
Etilene	28,054	296,37	1548,2	1251,8	1,237
Elio	4,003	2077,03	5192,6	3115,6	1,667
Idrogeno	2,016	4124,18	14209,1	10084,9	1,409
Metano	16,04	518,35	2253,7	1735,4	1,299
Neon	20,183	411,95	1029,9	617,9	1,667
Azoto	28,013	296,80	1041,6	744,8	1,400
Ottano	114,23	72,79	1711,3	1638,5	1,044
Ossigeno	31,999	259,83	921,6	661,8	1,393
Propano	44,097	188,55	1679,4	1490,9	1,126
Vapore acqueo	18,015	461,52	1872,3	1410,8	1,327

Tabella B – Capacità termica specifica in funzione della temperatura di alcuni gas perfetti

Temperatura [K]	Cp [kJ/kgK]	Cv [kJ/kgK]
ARIA
300	1,0035	0,7175	1,400
400	1,013	0,7263	1,395
500	1,029	0,7424	1,386
600	1,051	0,7639	1,376
700	1,075	0,7878	1,365
800	1,099	0,8116	1,354
ANIDRIDE CARBONICA
300	0,8418	0,6529	1,289
400	0,9390	0,7501	1,252
500	1,014	0,8250	1,229
600	1,075	0,8863	1,213
700	1,126	0,9372	1,201
800	1,169	0,9797	1,193
AZOTO
300	1,0416	0,7448	1,400
400	1,044	0,7472	1,397
500	1,056	0,7591	1,391
600	1,075	0,7780	1,382
700	1,098	0,8010	1,371
800	1,122	0,8252	1,360
OSSIGENO
300	0,9216	0,6618	1,393
400	0,9409	0,6810	1,382
500	0,9716	0,7118	1,365
600	1,003	0,7431	1,350
700	1,031	0,7709	1,337
800	1,054	0,7945	1,327