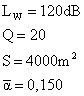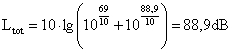Gianluca Ficarelli – matr. 125358 – Lezione del 27/11/2000 – ora 16:30-18:30

Propagazione negli spazi chiusi

1. Sorgenti immagine e cammini riflessi

All’interno di un ambiente chiuso tutti i fenomeni atmosferici caratteristici degli spazi aperti sono trascurabili; quindi, possiamo supporre sempre l’aria ferma, la temperatura uniforme e le direzioni di propagazione del suono rettilinee.

Consideriamo una sorgente stazionaria puntiforme, che emette fronti d’onda sferici di uguale intensità in tutte le direzioni, all’interno di una stanza a forma di parallelepipedo e priva di ostacoli interni, rappresentata in due dimensioni in figura 1.

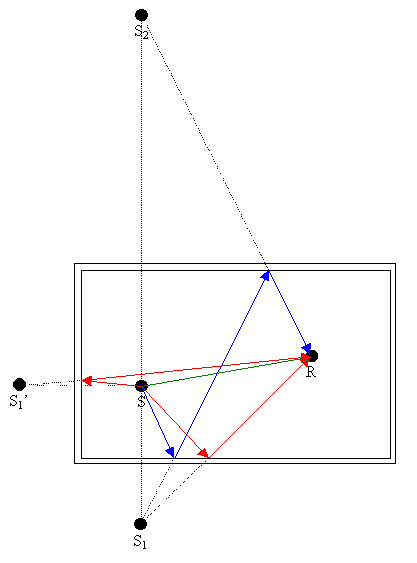
Figura 1 – Proiezione bidimensionale di un ambiente chiuso a forma di parallelepipedo e rappresentazione di alcune sorgenti immagine e alcuni cammini riflessi del primo e del secondo ordine.

Il cammino di propagazione diretto, percorso dall’onda sonora senza subire alcuna riflessione, si ottiene congiungendo idealmente con un tratto rettilineo la sorgente e il ricevitore. Questo non è l’unico cammino possibile: dal punto di vista energetico, infatti, il grosso della propagazione è spesso dovuto alla riflessione contro le pareti della stanza e avviene lungo cammini più lunghi e complicati.

Costruiamo una sorgente immagine S₁ specularizzando la sorgente reale rispetto a una delle pareti. Attraverso semplici considerazioni geometriche, siamo in grado di tracciare il percorso seguito dall’onda sonora, trovando così un cammino riflesso. La lunghezza del cammino riflesso è esattamente uguale alla distanza tra la sorgente immagine S₁ e il ricevitore. Sorgente immagine e cammino riflesso sono detti del primo ordine perché l’onda ha subito una sola riflessione. Un ragionamento analogo può essere fatto per ognuna delle sei pareti della stanza: avremo quindi sei sorgenti immagine e sei cammini riflessi del primo ordine.

A sua volta, ognuna delle sei sorgenti immagine del primo ordine può essere specularizzata rispetto a una delle altre cinque pareti: quindi, possiamo costruire trenta sorgenti immagine e trenta cammini riflessi del secondo ordine.

Proseguendo in questo ragionamento, abbiamo:

6	sorgenti immagine del 1° ordine
6*5 = 30	sorgenti immagine del 2° ordine
305 = 65*5 = 150	sorgenti immagine del 3° ordine
1505 = 6555 = 750	sorgenti immagine del 4° ordine
…	…
6*5^n-1	sorgenti immagine del n-esimo ordine

All’aumentare dell’ordine della sorgente immagine, avvengono due fatti importanti:

- aumenta la distanza della sorgente dal ricevitore e, di conseguenza, diminuisce il contributo energetico del singolo raggio riflesso;

- il numero totale di raggi riflessi cresce in modo esponenziale.

A causa dell’aumento esponenziale del numero di raggi, anche se l’energia trasportata da ciascun raggio riflesso tende a diminuire, complessivamente non è trascurabile nemmeno l’energia dei cammini di ordine elevato. Nello studio della propagazione del suono, di conseguenza, se si considerano soltanto gli ordini di riflessione più bassi, si trascura una parte ancora importante dell’energia e la descrizione dell’evento non è corretta. Per rappresentare in modo efficace il fenomeno sonoro, occorre studiare un numero elevatissimo di sorgenti immagine.

2. Sorgente stazionaria interrotta e tempo di riverberazione

Supponiamo che la sorgente abbia potenza nulla fino al tempo t = 0; a questo punto, il livello di potenza passa improvvisamente da 0 al valore L_s e rimane costante per un tempo t_s = 20s, per poi tornare istantaneamente a 0 (Figura 2).

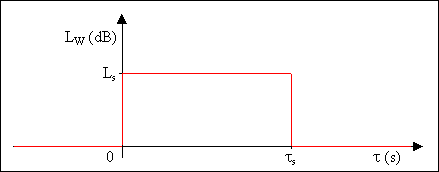
Figura 2 – Andamento nel tempo del livello di potenza della sorgente.

Analizziamo il livello di intensità prodotto sul ricevitore.

Prima che il suono diretto emesso dalla sorgente arrivi al ricevitore trascorre un tempo t₀, detto tempo di propagazione dell’onda sonora, uguale al rapporto tra la distanza della sorgente dal ricevitore e la velocità del suono.

Per esempio, supponiamo che il ricevitore si trovi a 15 metri dalla sorgente: il tempo di propagazione vale t₀ = 15/343 = 0,044s = 44ms, valore non trascurabile per il sistema uditivo umano. Se nello stesso ambiente si trova un altoparlante alla distanza di 4 metri dall’ascoltatore, il suono prodotto da questo altoparlante arriva con un ritardo nettamente inferiore (4/343 = 0,012s = 12ms), poiché la propagazione elettrica è praticamente istantanea se paragonata a quella acustica. Siccome il sistema percettivo umano è affetto da un fenomeno chiamato effetto Haas ovvero effetto di precedenza, secondo cui l’ascoltatore tende a localizzare il luogo da cui giunge il suono in base alla provenienza del primo fronte sonoro, si monta una linea elettrica di ritardo sugli altoparlanti, in modo che il suono prodotto da questi arrivi simultaneamente o immediatamente dopo il suono diretto. Nell’esempio, il ritardo dovrà essere di almeno 44–12 = 32ms.

Il campo sonoro si mantiene al livello L₀ = L_W–11–20lg r, finché arriva la prima onda riflessa, poi il livello totale si trova sommando i livelli del suono diretto e del suono riflesso.

Se la sorgente è coerente, la superficie non è diffondente e la riflessione è speculare, allora occorre considerare i possibili fenomeni di interferenza e la somma deve essere fatta in modulo e fase.

Se invece la sorgente è incoerente oppure la superficie non è perfettamente speculare ma è diffondente, allora occorre combinare energeticamente il suono riflesso col suono diretto: questo è ciò che avviene nella maggior parte dei casi pratici.

Trascorso un ulteriore ritardo, inferiore a quello precedente, arriva un altro suono riflesso e il livello totale aumenta di un altro gradino.

I suoni riflessi successivi giungono sempre più ravvicinati: il livello totale non ha più un andamento a gradini, ma aumenta in modo continuo, seguendo una curva che tende al valore di regime L_reg. Questo valore viene raggiunto quando si stabilisce un bilancio tra l’energia emessa dalla sorgente e quella assorbita dalle pareti.

Questo bilancio energetico può essere paragonato alla situazione che si raggiunge quando si versa acqua attraverso un rubinetto in un secchio con il fondo bucherellato: il livello che si stabilisce deriva dal bilanciamento tra l’acqua che esce dai fori e quella che entra dal rubinetto.

Dal momento in cui viene spenta la sorgente, trascorre di nuovo un tempo t₀ affinché il livello totale cominci a scendere: si esaurisce per primo il contributo del suono diretto e si ha un piccolo gradino, perché ora il grosso dell’energia è dovuto al suono riflesso; successivamente, scompaiono i contributi dei suoni riflessi.

In figura 3 è rappresentato il diagramma del livello di intensità prodotto sul ricevitore: si ottiene una curva di decadimento che, a differenza della curva di carico, ha un andamento rettilineo.

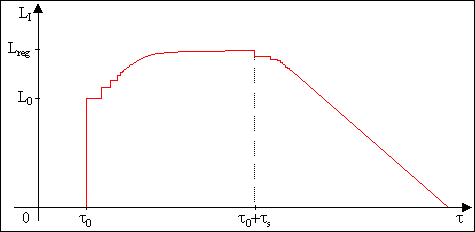
Figura 3 – Livello di intensità nel tempo.

Il persistere per un certo tempo del suono nell’ambiente, dopo che l’evento sonoro è terminato, viene chiamato fenomeno della coda sonora o riverberazione.

Nel 1902, W. C. Sabine diede la seguente definizione il tempo di riverberazione, o durata convenzionale della coda sonora: data una sorgente stazionaria interrotta, il tempo di riverberazione è il tempo che intercorre tra l’istante in cui si esaurisce il suono diretto e l’istante in cui il livello sonoro è sceso di 60 dB; esso viene indicato con T₆₀.

Il tempo di riverberazione è una caratteristica dell’ambiente e non deve dipendere dal livello sonoro del segnale: se esso fosse misurato fino all’esaurimento completo della coda sonora, invece, a un segnale con livello elevato corrisponderebbe un tempo di riverberazione maggiore e a un segnale con livello basso corrisponderebbe un tempo di riverberazione minore.

Per realizzare una misurazione del tempo di riverberazione secondo la definizione di Sabin, sarebbe necessario misurare un decadimento di 60 dB, ottenibile soltanto con una sorgente molto forte e un rumore di fondo molto basso; in molti ambienti ciò non è possibile, in quanto il rumore di fondo è troppo elevato.

La misura pratica è definita dalla norma ISO 3382 del 1997, molto recente perché le tecniche di misura del decadimento sonoro si sono evolute enormemente nell’ultimo decennio.

Questa norma prevede due possibili misure, T₂₀ e T₃₀, definite in questo modo:

T₂₀ (oppure T₃₀) è il tempo necessario affinché il suono scenda da –5 dB a –25 dB (oppure da –5 dB a –35 dB) rispetto al livello del regime stazionario, moltiplicato per 3 (oppure per 2), in modo che T₂₀, T₃₀ e T₆₀ siano confrontabili tra di loro.

Il tempo di riverberazione è sempre il tempo necessario affinché il suono decada di 60 dB; tuttavia, T₆₀ è misurato su un effettivo decadimento di 60 dB mentre T₂₀ e T₃₀ sono misurati su un decadimento rispettivamente di 20 dB e di 30 dB e devono essere estrapolati. Quindi, se il decadimento e perfettamente rettilineo, T₂₀ = T₃₀ = T₆₀; in generale, a causa della presenza del rumore di fondo, la curva di decadimento non è perfettamente rettilinea e questi valori non sono identici.

T₂₀ e T₃₀, a differenza di T₆₀, sono misurabili facilmente: infatti, mentre un decadimento di 60 dB è irrealizzabile nella maggior parte dei casi, un decadimento di 20 dB o 30 dB è ottenibile senza difficoltà.

In figura 4 sono rappresentati graficamente T₂₀, T₃₀, T₆₀ su una possibile curva di decadimento.

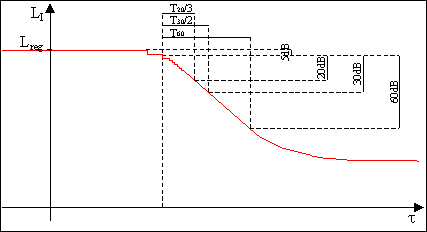
Figura 4 – T₂₀, T₃₀, T₆₀ sulla curva di decadimento.

3. Sorgente impulsiva e tempo di riverberazione

La definizione di tempo di riverberazione è basata sull’impiego di una sorgente stazionaria interrotta: quindi, occorrerebbe un’eccitazione di lunghezza elevata per portare il livello sonoro a regime. Tuttavia, in pratica si preferisce utilizzare un segnale impulsivo che costituisca una buona approssimazione della funzione di Dirac, come quello rappresentato in figura 5.

Figura 5 – Segnale impulsivo approssimante la funzione di Dirac.

All’istante t = 0 la sorgente emette un impulso di lunghezza temporale molto piccola e di livello abbastanza elevato. Dal punto di vista percettivo umano, un segnale può essere considerato un segnale impulsivo se la sua durata temporale è una frazione di millisecondo. Per questo motivo, spesso si utilizza un colpo di pistola.

Trascorso il tempo t₀ dall’emissione del suono, l’impulso giunge al ricevitore, il livello di intensità passa istantaneamente a L₀ e torna a 0.

Dopo qualche millisecondo arriva la prima onda riflessa, il cui livello è più basso di quello del suono diretto perché ha fatto un cammino più lungo e perché ha perso energia per effetto dell’assorbimento sulla superficie di riflessione.

Trascorre altro tempo e arriva la seconda onda riflessa, poi la terza e poi le altre, sempre più deboli e vicine ma ancora separate.

Dopo una decina di riflessioni, le onde riflesse non sono più separate, perché il ritardo tra un’onda e quella successiva diventa confrontabile con la durata del segnale stesso: si ottiene una coda continua che decade verso 0, come quella rappresentata in rosso in figura 6.

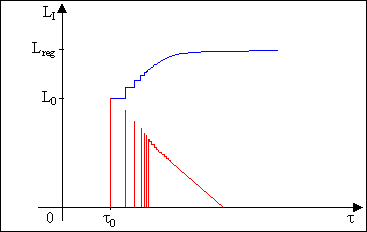
Figura 6 – Risposta impulsiva (in rosso) e sua integrazione nel tempo (in blu).

Integrando l’intensità del suono nel tempo (tra 0 e t) e passando al corrispondente livello di intensità, si ottiene la curva di carico rappresentata in blu in figura 6.

L’intensità a regime vale:

(1)

Conoscendo la risposta all’impulso e utilizzando il metodo di integrazione all’indietro di Schröder, descritto nella norma ISO 3382, è possibile ricostruire matematicamente l’andamento del livello di intensità sul ricevitore nel caso in cui una sorgente stazionaria venisse interrotta, ma senza dovere realizzare fisicamente la misura.

Il metodo di integrazione all’indietro consiste nel togliere al livello di regime prima il suono diretto, poi il primo suono riflesso, poi tutti gli altri suoni riflessi in successione, ottenendo così la curva di decadimento:

(2)

La curva di scarico può essere ricostruita facilmente utilizzando un foglio di calcolo come Excel: infatti, è sufficiente campionare la forma d’onda ed inserire le formule e i dati necessari nelle celle, sostituendo gli integrali con sommatorie finite.

4. Formula di Sabin

Cerchiamo il legame tra il valore del tempo di riverbero e le caratteristiche geometriche e di assorbimento acustico dell’ambiente chiuso.

Supponiamo che l’ambiente abbia un certo volume V espresso in m³ e che sia circondato da N pareti, ciascuna avente un valore di superficie S_i in m² e ciascuna avente un valore locale del coefficiente di assorbimento acustico a_i, dipendente dalla frequenza.

Sabin trovò in modo sperimentale la seguente relazione, dimostrata da Knudsen sotto ipotesi molto restrittive solo una trentina di anni dopo:

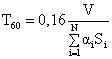(3)

0,16 non è un coefficiente, ma è una quantità dimensionata; tuttavia, possiamo scrivere: , dove c è la velocità del suono e 55,3 è un numero puro.

Se definiamo il coefficiente di assorbimento acustico medio 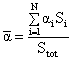, possiamo riscrivere la formula (3) nel modo seguente:

(4)

Dalla formula (3) oppure (4) si deduce che il tempo di riverbero dell’ambiente cresce all’aumentare del volume e al diminuire della superficie assorbente. Inoltre, esso dipende dalla frequenza del suono, poiché anche i coefficienti acustici dei materiali che costituiscono le pareti vi dipendono.

La formula di Sabin non è l’unica possibile: infatti, esistono formule migliori e più complicate come quella di Eyring e quella di Millington, ma sono poco utilizzate.

5. Livello del campo riverberante e semiriverberante

Consideriamo una sorgente stazionaria in un ambiente chiuso.

A breve distanza dalla sorgente vale la legge del campo libero, secondo la quale il livello sonoro diretto vale:

(5)

dove:

Q è il fattore di direttività della sorgente;

r è la distanza tra sorgente e ricevitore.

All’aumentare della distanza dalla sorgente, il livello di intensità devia da questa legge e raggiunge il valore di regime L_reg nella regione di campo riverberante; questo livello sonoro è dovuto soltanto al suono riverberante e secondo Sabin vale:

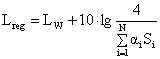(6)

Tra la regione di campo libero e la regione di campo riverberante, si trova una regione intermedia detta di campo semiriverberante, nella quale non sono trascurabili né il contributo dovuto al suono diretto (livello diretto), né il contributo dovuto al suono riverberante (livello a regime).

La legge che descrive l’andamento del livello sonoro in funzione della distanza si ottiene sommando energeticamente questi due contributi, in quanto i due fenomeni sono sempre incoerenti tra loro; si ottiene:

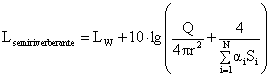(7)

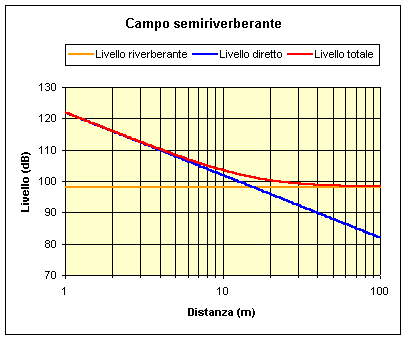
Figura 7 – Dipendenza del livello di intensità dalla distanza secondo la legge del campo semiriverberante.

6. Distanza critica

Definiamo distanza critica la distanza alla quale il livello del campo diretto e il livello del campo riverberante assumono lo stesso valore, cioè L_dir = L_reg: di conseguenza, il rapporto R/D = L_reg – L_dir deve essere nullo.

Imponendo l’uguaglianza

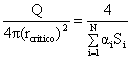(8)

otteniamo:

(9)

Se l’ascoltatore si trova a una distanza inferiore di r_critico, il suono che lo raggiunge è intelligibile anche se l’ambiente ha un riverbero elevato.

7. Tempo di riverberazione ottimo

La formula (7) del campo semiriverberante non mostra l’andamento temporale del livello sonoro, ovvero non permette di valutare il tempo che l’energia dovuta al campo riverberante impiega per propagarsi, ma è molto utile negli ambienti di lavoro.

Negli spazi destinati all’ascolto della parola o della musica, invece, non è rilevante soltanto il livello del suono che giunge alle orecchie degli ascoltatori: è molto importante anche la qualità del suono. Non devono verificarsi fenomeni di interferenza, ma soprattutto deve essere garantita la chiarezza e l’intelligibilità della parola: in altre parole, i suoni devono arrivare distinti all’ascoltatore.

Il linguaggio parlato è costituito da suoni elementari quasi impulsivi, chiamati fonemi; ogni fonema non coincide necessariamente con una lettera. La comprensione del linguaggio consiste nel corretto riconoscimento della sequenza fonetica, possibile soltanto se i fonemi sono sufficientemente distanziati tra di loro.

A causa del fenomeno della riverberazione, la coda sonora di ogni fonema può sovrapporsi al fonema successivo: questo è il motivo per cui un tempo di riverberazione eccessivo può impedire l’identificazione dei fonemi e la corretta comprensione del linguaggio parlato.

Poiché la lunghezza dei fonemi dipende dalla velocità e dalla lingua in cui parla l’oratore, il tempo di riverberazione di una sala può essere adeguato a un parlatore italiano, ma assolutamente inadatto a un parlatore straniero: la lingua italiana, infatti, è costituita da fonemi più netti e distanziati rispetto ad altre lingue come quella inglese. Inoltre, una persona che parla in un ambiente riverberante tende autonomamente a rallentare il discorso e a cadenzare maggiormente le sillabe: ciò riduce il problema della riverberazione; tuttavia, in alcune lingue, come in quella inglese, la durata delle sillabe non può essere variata arbitrariamente, perché anche questa durata ha un significato.

In base all’utilizzo di ogni ambiente, esiste un valore ottimale del tempo di riverberazione: questo tempo non deve essere troppo basso, perché sarebbe come parlare all’aperto e il livello sonoro rimarrebbe troppo debole; tuttavia, non deve essere nemmeno troppo elevato, perché sarebbe penalizzata la comprensione del linguaggio.

Esistono tabelle e grafici che riportano il tempo ottimale di riverberazione in funzione del volume e dell’utilizzo dell’ambiente.

Una prima distinzione può essere fatta valutando se l’ambiente è finalizzato all’ascolto di linguaggio parlato o di musica: l’ascolto di linguaggio parlato necessita tempi di riverberazione inferiori.

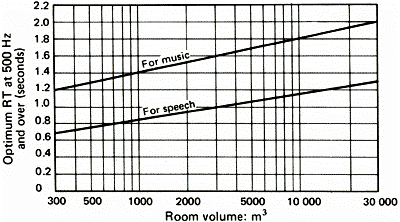
Figure 8 e 9 – Tempo di riverberazione ottimale in funzione del volume e dell’utilizzo dell’ambiente.

Ambiente	T_opt (secondi)
Aula scolastica piccola	0,5
Aula scolastica grande	1
Cinema	0,7 ÷ 0,8
Teatro d’opera (musica lirica)	1,3 ÷ 1,5
Sala da concerto (musica sinfonica)	1,7 ÷ 2,3
Chiesa (musica sacra)	2,5 ÷ 5

Già in fase di progetto di un locale, occorre saper variare la superficie e il coefficiente di assorbimento acustico delle pareti per avvicinarsi al tempo di riverberazione ottimale a tutte le frequenze.

Il Decreto Ministeriale del 18/12/1975 fissa il massimo valore del tempo di riverberazione di un aula scolastica in funzione del volume e della frequenza. Alle basse frequenze la tolleranza è maggiore ed è consentito avere tempi più elevati; inoltre, più è grande il locale più il tempo di riverberazione deve essere alto, affinché anche gli ascoltatori più lontani possano udire l’oratore.

Questo decreto fissa i limiti ad aula vuota (devono essere presenti al massimo due persone): infatti, le persone hanno un coefficiente di assorbimento acustico che vale circa 0,8 e sono una delle fonti di assorbimento più importanti un locale.

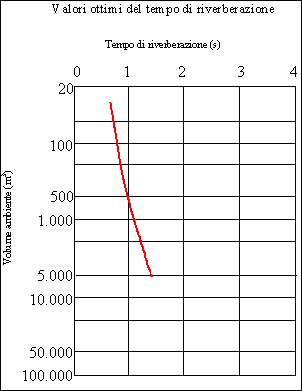
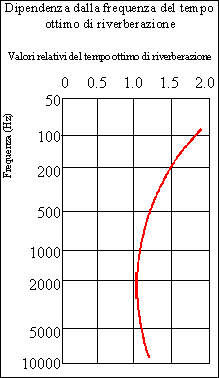
Figure 10 e 11 – Tratte dal D.M. del 18/12/1975.

(Dati non ufficiali: fare riferimento alla documentazione originale)

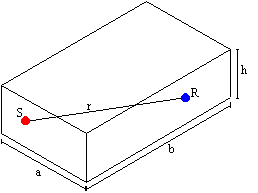
Esercizio

Sia data una stanza a forma di parallelepipedo come quella in figura 12.

Sapendo che il coefficiente di assorbimento acustico del pavimento vale a₁, quello delle pareti laterali vale a₂, quello del soffitto vale a₃, calcolare il tempo di riverberazione T₆₀.

Se il livello di potenza della sorgente vale L_W e la distanza tra sorgente e ricevitore vale r, calcolare il livello diretto L_dir, il livello riverberante L_riv, il livello totale L_tot, il rapporto R/D tra livello riverberante e livello diretto, la distanza critica r_critico.

a = 10 m

b = 6 m

h = 4 m

a₁ = 0,05 (pavimento)

a₂ = 0,1 (pareti laterali)

a₃ = 0,6 (soffitto)

L_W = 100 dB

r = 10 m

Figura 12.

Supponiamo che valgano le relazioni di Sabin.

Ricaviamo per comodità la quantità:

Ricordando la formula (3) oppure (4), otteniamo il tempo di riverberazione:

Utilizzando le formule (5) e (6), ricaviamo il livello diretto e riverberante:

Sommando il livello diretto e il livello riverberante otteniamo il livello totale:

Il rapporto R/D vale:

Il ricevitore si trova in una zona di campo completamente riverberante, nella quale il suono diretto si è perso completamente e l’intelligibilità della parola è bassa. Per ovviare a questo problema, si ricorre spesso all’uso di altoparlanti.

Servendoci della formula (9), troviamo la distanza critica: