Elaborazione numerica dei segnali
L’elaborazione numerica dei segnali ( DSP Digital Signal Processing ) è una scienza giovane, che ha avuto il suo massimo sviluppo negli ultimi 15 anni grazie ai progressi compiuti dai componenti elettronici ad altissima integrazione, e alla nascita degli omonimi processori specializzati utilizzati per l'elaborazione. Attualmente l’impiego di questi processori dedicati nella maggior parte dei casi è limitato alle tecnologie di basso costo quali la telefonia cellulare, altrove si preferisce l’impiego dei calcolatori elettronici che garantiscono a parità di prestazione una maggior praticità nella programmazione.
L’analisi computerizzata di un segnale audio analogico (cioè caratterizzato da infiniti valori che variano con continuità secondo una funzione del tempo) richiede la conversione del segnale in digitale in modo particolare in un segnale digitale binario costituito da una sequenza dei soli valori 0-1, così da consentirne l’elaborazione tramite una CPU.
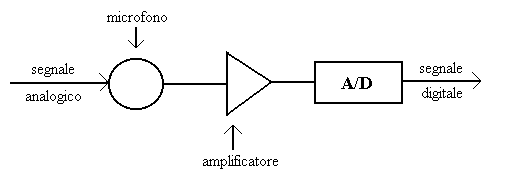
La conversione viene effettuata tramite un convertitore analogico-digitale (A/D) inserito in un circuito schematizzato dal seguente diagramma a blocchi.

Figura 1
Il segnale utile che deve essere registrato è la variazione di pressione acustica prodotta dalla sorgente del segnale stesso. Tale segnale viene convertito in una debole tensione elettrica dal microfono, che svolge la funzione trasduttore (cioè di dispositivo che cambia la natura del segnale senza alterarne la forma). La tensione prodotta dal microfono, prima di poter essere elaborata ulteriormente, deve essere amplificata dall'amplificatore. Sia microfono che amplificatore sono componenti analogici, infatti l'andamento della tensione prima e dopo l'amplificazione è analogo alla pressione acustica in ingresso a meno di una costante moltiplicativa. A questo punto entra in azione il convertitore A/D.
La mappatura del segnale analogico da parte del convertitore A/D viene effettuata tramite due operazioni: il campionamento e la quantizzazione.
Il campionamento consente di ottenere un segnale a tempo discreto, cioè una successione o sequenza x[n] di numeri rappresentabile con una funzione di variabile intera relativa avente valori reali o complessi, partendo dal segnale analogico.
Campionare un generico segnale x(t) significa "estrarre" dal segnale stesso i valori che esso assume a istanti temporali equispaziati, cioè multipli di un intervallo T detto periodo di campionamento. Con questa operazione viene a crearsi una sequenza il cui valore n-esimo x[n] è il valore assunto dal segnale a tempo continuo all’istante nT: x[n]=x(nT).
L’operazione di campionamento viene simbolicamente effettuata da un dispositivo, il campionatore, indicato con una sorta di interruttore che si chiude per un intervallo di durata infinitesima. La cadenza con cui l’interruttore si chiude è pari a:
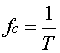 (1)
(1)
e prende il nome frequenza di campionamento (sampling frequency), misurata in Hz o in campioni/secondo. Prima dell'avvento del digitale il campionamento era ottenuto tramite filtri analogici passivi, la cui curva di risposta in frequenza approssimava con curve gaussiane lo spettro delle odierne bande, e in cui veniva fatto passare il segnale. In Figura 2 è rappresentato un generico segnale analogico in funzione del tempo t, si può vedere come varii con continuità. L in ordinata rappresenta il livello del segnale, che per i segnali acustici è solitamente espressa in decibel (dB).
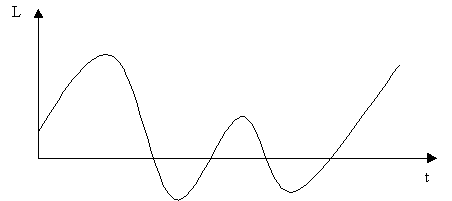
Figura 2: Piano analogico
La Figura 3 rappresenta il corrispettivo digitale del precedente segnale analogico: in questo caso si vede chiaramente che abbiamo a che fare con una sequenza discreta di valori e non più con un continuo, coi valori della sequenza che distano tra loro un tempo T pari al periodo di campionamento.
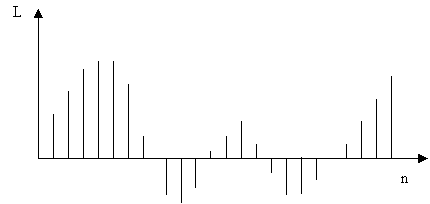
Figura 3: Piano digitale
Il convertitore A/D è comandato da un segnale di clock (temporizzazione) alla frequenza di campionamento. Il campionatore ideale estrae in corrispondenza di ogni impulso di clock il valore del segnale in ingresso all'istante di campionamento, che è in generale un numero reale con infinite cifre decimali. Diversamente dal campionatore ideale, il convertitore A/D rende invece una rappresentazione finita di questo numero reale (segnale numerico), e precisamente in aritmetica binaria su un numero finite di cifre (bit), variabile da 8 a 24. Il piccolo errore insito nella rappresentazione del numero reale su un numero finito di cifre rappresenta la seconda operazione del convertitore: la quantizzazione. Di fatto quindi il convertitore effettua una doppia operazione di "discretizzazione": la prima sull'asse dei tempi, dove determina gli istanti in cui si deve considerare il segnale; la seconda sull'asse delle ampiezze dove il segnale viene approssimato al "quanto" più vicino in base alla risoluzione in bit del convertitore.
I convertitori A/D sono caratterizzati da due parametri fondamentali:
I convertitori tipici sono a 16 bit corrispondenti ad una frequenza di campionamento di 44.1 kHz che in alcune schede audio può essere portata fino a 48. I 16 bit impongono che il valore del segnale debba appartenere all'intervallo che va da -32767 a +32767. Su un simile intervallo l'errore di quantizzazione commesso dal convertitore non è trascurabile, di fatto quindi si introduce un rumore che fa dello standard audio a 16 bit uno standard di basso livello. Per questo motivo nelle applicazioni professionali si utilizzano convertitori che hanno 24 bit di livelli possibili in ampiezza e frequenza di campionamento a 96 kHz. In questo caso l'errore assoluto di quantizzazione è lo stesso, ma distribuito su un intervallo di possibili valori delle ampiezze maggiore, e quindi il rumore introdotto è molto inferiore. Infatti con la risoluzione a 24 bit il rapporto fra segnale e rumore è molto elevato, pari a 196 dB.
Le approssimazioni introdotte dai convertitori nella trattazione dei segnali porta a dover considerare distintamente due settori di ricerca dell'acustica: la metrologia e l'elettroacustica.
Scopo della prima è compiere misure del segnale, che una volta campionato non viene più riconvertito in analogico. La seconda si occupa di elaborare il segnale digitale per poi riconvertirlo in modo che sia il più possibile simile al segnale ricevuto, o comunque tale da poter essere utilizzato. Nel fare ciò nella maggior parte dei casi si va incontro, volutamente, ad una perdita di dati del segnale accettabile ai fini dell'elettroacustica, ma non a quelli della metrologia. Un caso tipico di elettroacustica è quello delle comunicazioni telefoniche, dove si preferisce una minor qualità del segnale, che comunque resta comprensibile, in favore di tecnologie più accessibili e pratiche, o dove comunque non esiste un interesse effettivo che giustifichi un'elaborazione più raffinata.
Teorema di Shannon
Il teorema di Shannon (o di Nyquist) fornisce la condizione necessaria affinché un segnale dopo il campionamento possa nuovamente essere ritrasformato in analogico, tramite un convertitore D/A riottenendo il segnale di partenza.
Teorema: la frequenza di campionamento di un segnale deve essere
![]() (2)
(2)
dove fmax rappresenta la frequenza massima contenuta nel segnale, ed è anche conosciuta come frequenza di Nyquist, mentre fc è la frequenza di campionamento.
Se nel campionare non si rispetta questa condizione, le componenti del suono a frequenza maggiore vengono sottocampionate e quindi ricompaiono nel segnale campionato come elementi a componenti frequenziali più basse secondo la seguente relazione:
![]() (3)
(3)
Se per esempio analizziamo al computer lo spettro di un segnale "sweep", cioè un segnale con frequenza variabile in modo progressivo nel tempo, sottocampionato, si può vedere come lo spettro salga fino ad una determinata frequenza per poi tornare indietro come se rimbalzasse su di essa. Il fenomeno appena descritto è noto col nome di aliasing.
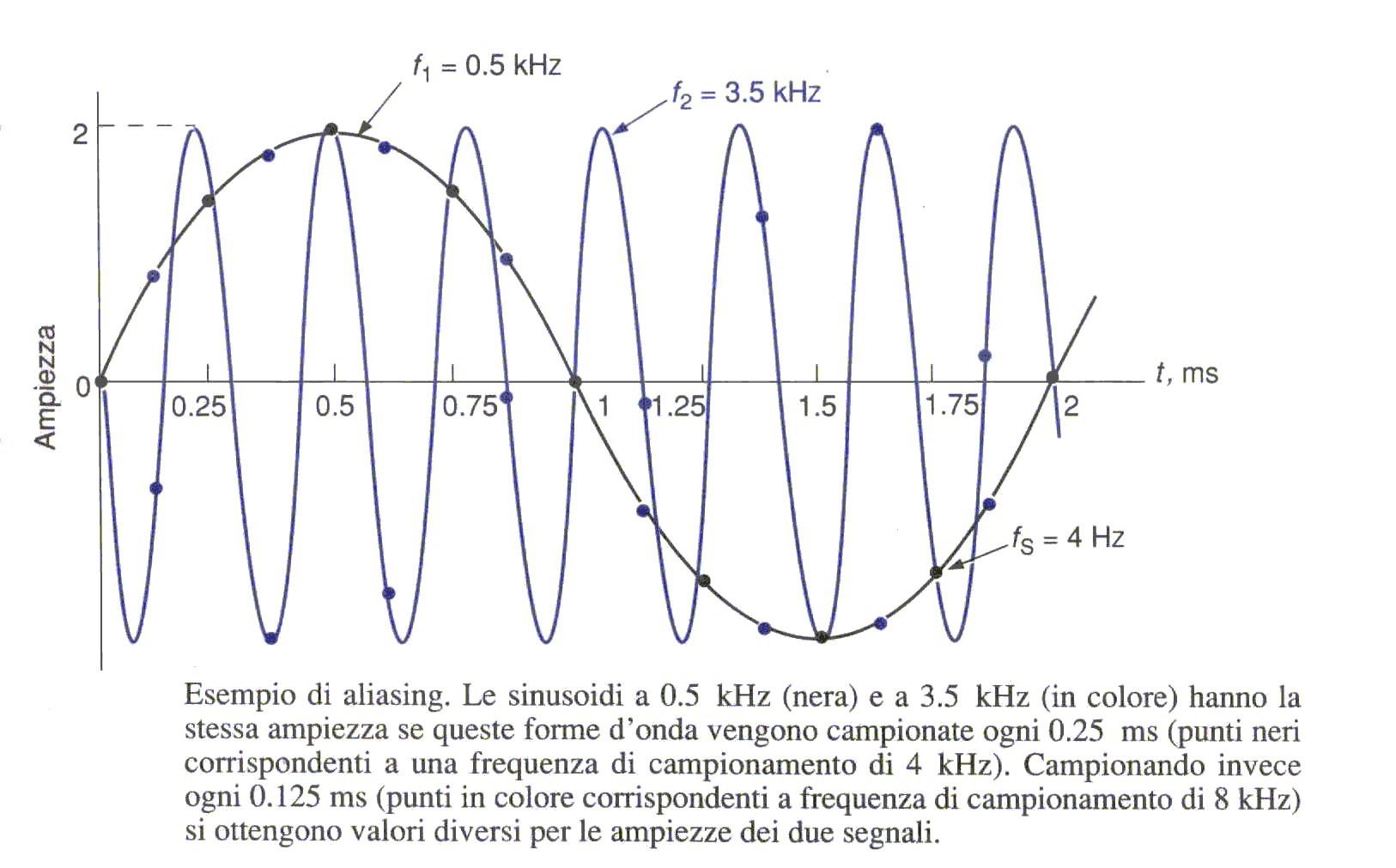
Figura 4: Aliasing
In generale lo spettro di una sequenza ottenuta per campionamento si ricava come periodicizzazione dello spettro del segnale analogico di partenza (Figura 5 a sinistra), con un periodo di ripetizione in frequenza pari alla frequenza di campionamento. Se però la frequenza di campionamento è tale che le varie repliche dello spettro centrate sui suoi multipli vengono a sovrapporsi (Figura 5 a destra), allora, interferiscono tra di loro sommandosi e generando l'errore di aliasing, e quindi la distorsione del segnale campionato.
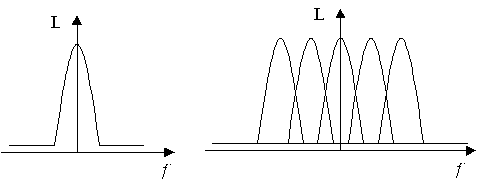
Figura 5
Se invece viene rispettata la condizione di Nyquist le diverse repliche dello spettro non si sovrappongono (Figura 6), consentendo di riprodurre il segnale senza distorsioni.
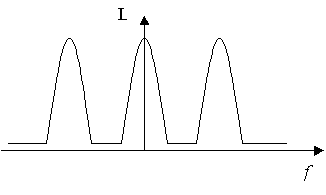
Figura 6
La frequenza limite utilizzabile per evitare aliasing è quella di Nyquist:
![]() (4)
(4)
Un'altra possibilità per evitare aliasing si presenta quando abbiamo a che fare con segnali a banda B limitata: in questo caso la condizione da rispettare è la seguente:
![]() (5)
(5)
Questa condizione ci suggerisce una tecnica per evitare problemi di aliasing:
si antepone al convertitore A/D di Figura 1 un filtro anti-aliasing che limiti la banda del segnale analogico ad un valore B' in modo da evitare l'aliasing per la frequenza di campionamento fissata.
Di fatto il filtro anti-aliasing si realizza tramite un filtro passa-basso in modo da eliminare dal segnale le frequenze più alte, cioè quelle superiori alla frequenza di Nyquist, che provocano aliasing. Chiaramente il taglio effettuato dal filtro deve essere tale da non ridurre eccessivamente la qualità del segnale stesso.
Un filtro passa-basso ideale ha un andamento caratterizzato da una caduta netta (Figura 7 in rosso). Di fatto però, tutti i filtri reali hanno una zona di caduta non trascurabile. L'ampiezza di questa è correlata al numero di bit del segnale e alla frequenza di Nyquist.
Un segnale per esempio a 16 bit ha un range in livello di 96 dB, ciò significa che un filtro per un segnale di questo tipo deve produrre una caduta di pari valore. Con una frequenza di campionamento di 44.1 kHz il filtro in questione è fisicamente realizzabile. I problemi sorgono quando si ha a che fare con segnali a 20 o più bit dove la caduta del filtro deve essere maggiore: la soluzione adottata è quella di aumentare la frequenza di campionamento (48-96 kHz) e quindi quella di Nyquist ampliando così sull'asse delle frequenze la zona di caduta del filtro che diviene realizzabile.
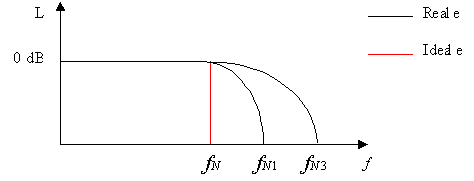
Figura 7: Filtri passa-basso
Oltre che per evitare l'aliasing, filtri come quelli appena descritti sono utilizzati quando il segnale audio campionato deve essere trasmesso, come in un sistema di radiodiffusione, dov'è importante ridurre al minimo il numero dei campioni/s. Infatti, più campioni devono essere trasmessi contemporaneamente, maggiore deve essere la capacità (e quindi il costo) del sistema di trasmissione. Per questo motivo in alcuni standard di radiodiffusione dell'audio digitale si campiona il segnale a 32 kHz. Questa frequenza non soddisfa chiaramente la condizione di Nyquist rispetto alla banda B=20 kHz, cioè la banda udibile dall'orecchio umano, ma l'uso del filtro anti-aliasing risolve il problema mantenendo su di un livello accettabile la qualità audio.
Analisi di Fourier e FFT
Teorema di Fourier: qualunque suono periodico è sempre rappresentabile come sovrapposizione di un opportuno numero d'onde sinusoidali (toni puri) di determinate ampiezze, frequenze e fasi:
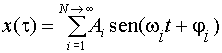 (6)
(6)
La dipendenza dalle frequenze della (6) è espressa dalla seguente relazione:
![]() (7)
(7)
Il teorema di Fourier è lo strumento matematico che nello studio dei segnali ci consente di passare dall'analisi nel dominio del tempo a quella nel dominio delle frequenze, tramite l'omonima trasformata, dove ad essere studiato è lo spettro del segnale in funzione della frequenza, con la possibilità tramite l'antitrasformata di tornare al dominio temporale.
Una delle esigenze più frequenti nell'elaborazione dei segnali è proprio quella di calcolare lo spettro, non di un segnale analogico ma di una sua sequenza x[n], ottenuta ad esempio tramite un convertitore A/D, di cui noi non conosciamo l'espressione analitica ma solo i valori della sequenza. Ciò che ci interessa è calcolare la trasformata di Fourier della sequenza x[n]:
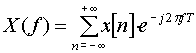 (8)
(8)
Questa operazione può essere eseguita velocemente dopo aver periodicizzato la sequenza, qualora non sia già periodica, tramite l'algoritmo di FFT (Fast Fourier Transform), scritto nel 1965 da Cooley e Tukey ; a questa data si fa risalire la nascita della moderna elaborazione numerica dei segnali. Tramite la FFT, infatti, si possono effettuare alcune operazioni essenziali sui segnali periodici quali l'analisi spettrale e il filtraggio tramite la convoluzione veloce.
Dopo l'operazione da analogico a digitale compiuta dal convertitore A/D possiamo pensare al segnale trattato come una sequenza di valori rappresentabile con un vettore di numeri interi tutti equidistanziati sull'asse dei tempi. Lo spettro del segnale così rappresentato può essere calcolato tramite la FFT, a cui, se pensiamo di avere memorizzato la sequenza su un calcolatore, viene fornito come parametro un puntatore al vettore dei dati e il numero N dei campioni che devono essere analizzati.
L'algoritmo opera sugli N campioni reali in ingresso trasformandoli in N/2+1 campioni complessi ciascuno costituito da una parte reale e da una parte immaginaria.
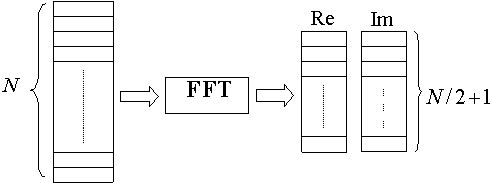
Figura 8: Schema di algoritmo FFT
![]() Dal punto di vista del calcolo della trasformata, l'algoritmo FFT è più efficace se nella sua esecuzione utilizziamo parte reale e parte immaginaria invece che ampiezza e fase, ricordandoci che è sempre possibile passare dalle prima alle seconde tramite le due relazioni espresse in Figura 9, dove A rappresenta l'ampiezza dello spettro e f la fase dello spettro.
Dal punto di vista del calcolo della trasformata, l'algoritmo FFT è più efficace se nella sua esecuzione utilizziamo parte reale e parte immaginaria invece che ampiezza e fase, ricordandoci che è sempre possibile passare dalle prima alle seconde tramite le due relazioni espresse in Figura 9, dove A rappresenta l'ampiezza dello spettro e f la fase dello spettro.
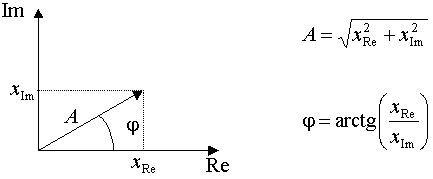
Figura 9
L'algoritmo FFT trasforma quindi il blocco di N campioni in righe spettrali; il primo elemento ha valore reale e rappresenta il valore medio del segnale, cioè la sua componente continua, ed è chiaramente una componente a frequenza nulla. Il secondo elemento, ha frequenza:
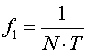 (9)
(9)
con T il periodo di campionamento. Le frequenze successive sono:
![]() (10)
(10)
con i=1,2,3...N/2 dove l'ultima frequenza è quella di Nyquist. Si ottiene così uno spettro costituito da righe spettrali equispaziate, con una risoluzione in frequenza determinata da f1. Una rappresentazione di questo tipo attribuisce la stessa importanza a tutte le frequenze sia basse che alte; in questo modo non si può privilegiare il campo delle basse frequenze, cioè quelle privilegiate dal sistema uditivo umano per la sua conformazione. Ne risulta che in generale si ottengono delle analisi spettrali troppo grossolane alle basse frequenze, e troppo precise rispetto alla sensibilità del nostro orecchio alle alte.
Poiché come si è visto il primo e l'ultimo spettro hanno solo componente reale, complessivamente dagli N campioni del segnale si ottengono N valori che rappresentano gli spettri, e che possono essere registrati nelle stesse locazioni di memoria dei campioni iniziali, in questo modo è possibile ottenere una sequenza di spettri che evolve nel tempo, e che si presta bene a due tipi di rappresentazione grafica:
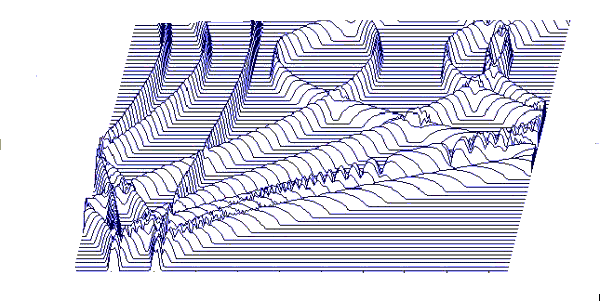
Figura 10: Waterfall
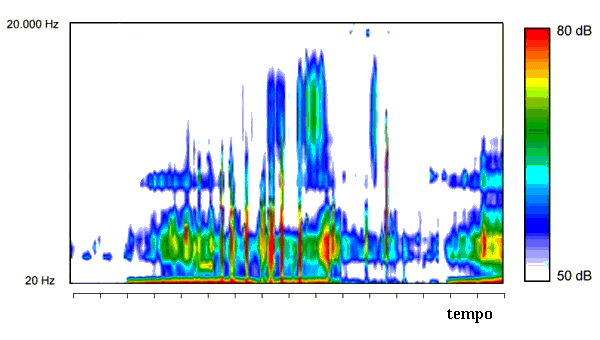
Figura 11: Sonogramma
Come si è detto sopra l'algoritmo FFT per funzionare opera su segnali periodici, cioè gli N campioni del blocco si devono ripetere per tutta la durata del segnale. Non sempre però il blocco di campionamento corrisponde ad un periodo o ad un numero intero di periodi. Ciò corrisponde ad avere l'ultimo campione diverso dal primo. Di fatto così facendo è come se analizzassimo un segnale differente in cui è presente un salto (Figura 12).
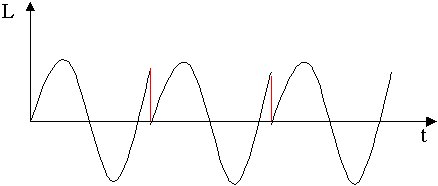
Figura 12
Dal punto di vista dell'analisi spettrale il salto della sinusoide appare come un gradino che altera lo spettro della sinusoide pura, estendedolo a tutte le frequenze, anziché avere una sola riga spettrale centrata in f0 come di solito compete agli spettri di una sinusoide.
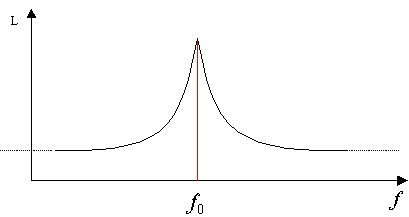
Figura 13
Il fenomeno dell'estensione dello spettro a tutte le frequenze è noto col nome di Leaking, ed è dovuto al fatto il salto che compare nel segnale ha uno spettro molto particolare detto rumore bianco. E' un rumore che ha uno spettro piatto in un analizzatore a banda stretta, a differenza del rumore rosa che ha spettro piatto in un analizzatore in terzi d'ottava. Il nome rumore bianco deriva dal fatto che comprende tutte le frequenze così come la luce bianca comprende tutta la banda dei colori.
Figura 14: Rumore bianco
Per risolvere il problema del leaking è necessario che il segnale si annulli agli estremi della finestra in cui sono contenuti gli N campioni; in questo modo abbiamo la certezza che il valore finale di una finestra coinciderà con quello iniziale della finestra successiva annullando il salto.
La soluzione consiste nell'applicare un filtro digitale al segnale campionato prima che questo venga trattato dall'algoritmo. Il filtro moltiplica il segnale per una funzione peso in modo tale da annullare il segnale agli estremi di ogni finestra. Esistono diverse funzioni peso, ma la più utilizzata è la Hanning, che a differenza delle altre (gaussiana, triangolare...) garantisce l'equivalenza energetica fra il segnale originario e quello pesato. La Hanning nel dominio del tempo non è altro che un coseno traslato sull'asse delle ordinate e normalizzato ad uno, questo fa si che il segnale rimanga inalterato al centro e si annulli agli estremi. Nel dominio delle frequenze il suo andamento assieme a quello di altre due finestre è mostrato in Figura 15.
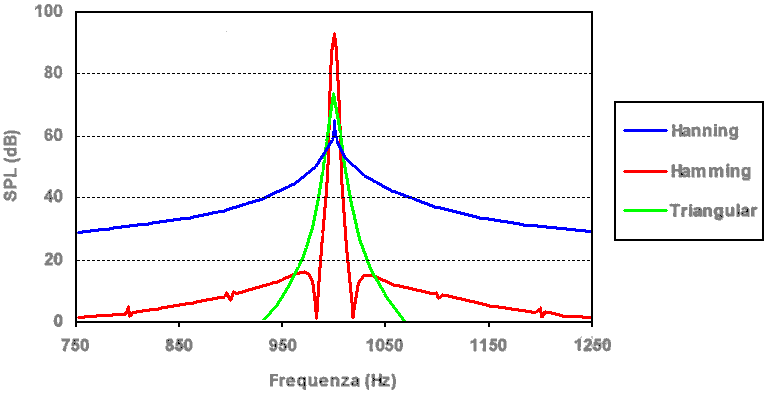
Figura 15
Una schematizzazione di come opera la Hanning sui campioni del segnale è data dalla Figura 16.
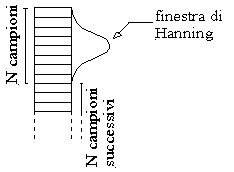
Figura 16: Finestra Hanning
Un uso della finestra Hanning come quello di Figura 16 è però insoddisfacente, perché chiaramente i campioni più accentrati rispetto alla finestra vengono pesati maggiormente rispetto ai campioni più esterni, e soprattutto rispetto agli estremi che vengono annullati. In questo modo mi ritrovo con un segnale che non è del tutto equivalente a quello in ingresso. Per non falsare l'analisi è necessario traslare tutte le finestre successive alla prima in modo tale da produrre una sovrapposizione tra le finestre stesse. Così facendo posso dare il giusto peso anche a quei campioni che in precedenza senza sovrapposizione erano stati sottostimati. Per la finestra Hanning la sovrapposizione ideale è del 50%, cioè devo ripetere una finestra ogni N/2 campioni (Figura 17). Questo valore dello shift è l'unico infatti che garantisce l'equivalenza energetica tra segnale originario e pesato, già citata in precedenza.
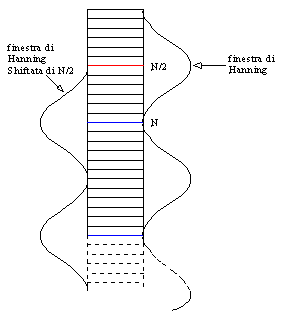
Figura 17: Sovrapposizione di finestre.