Cosimo Fadda matr.125354 Lezione del 16/10/2000 ore 16.30-18.30
Calcolo delle proprietà delle sostanze chimicamente pure (II°)
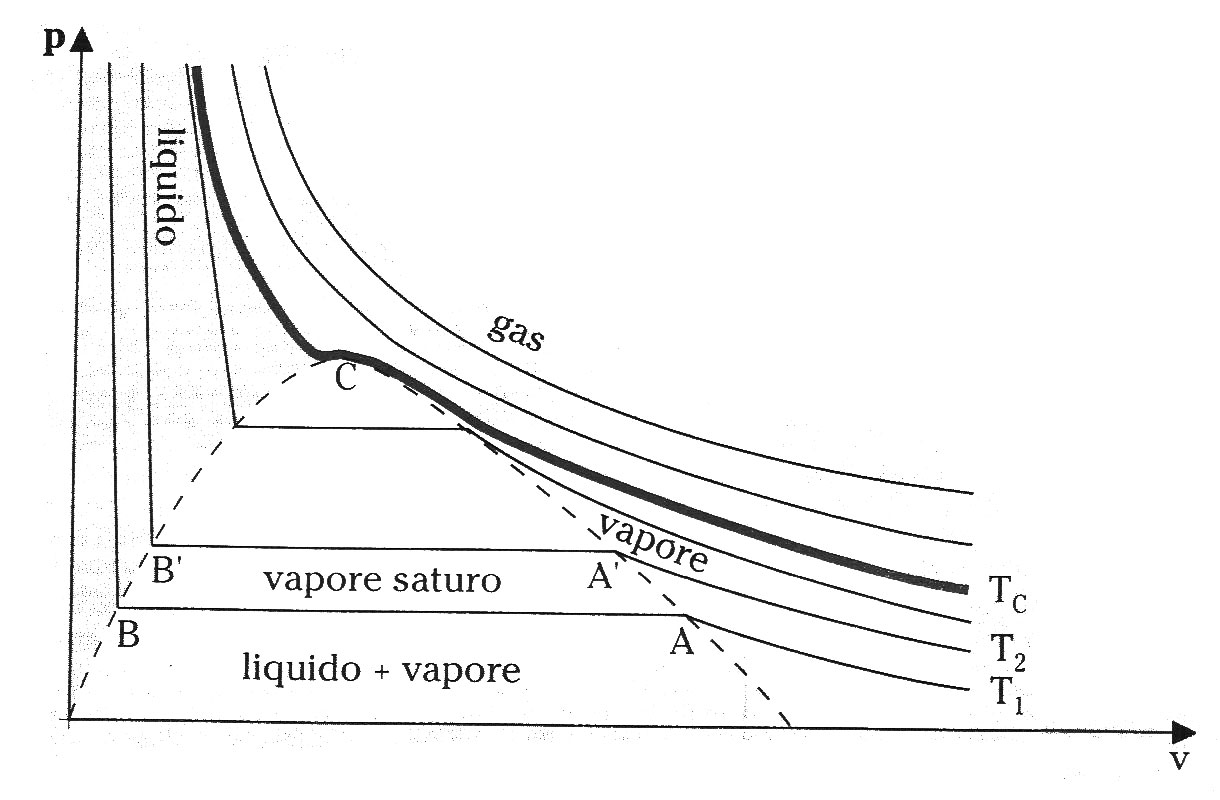
In questa lezione completeremo la mappatura del diagramma pv (fig.1) rivolgendo la nostra attenzione alle zone relative ai vapori surriscaldati e ai gas perfetti studiandone le loro proprietà che, assieme a quelle viste nella lezione precedente, ci daranno un quadro completo sulle proprietà dei sistemi chimicamente omogenei.

(fig.1 diagramma pv completo)
Proprietà dei vapori surriscaldati
I vapori surriscaldati si trovano nella zona del diagramma pv (fig.1) compresa tra la curva limite inferiore e l'isoterma critica. Questi si distinguono dai vapori saturi per la totale assenza di liquido. Il termine "surriscaldato" può essere ambiguo in quanto induce a far pensare che vi sia un riferimento al valore assoluto della temperatura mentre cosi non è, infatti, anche a temperatura ambiente possono trovarsi vapori nello stato di surriscaldamento. Questo succede ad esempio per il vapor d'acqua presente nell'aria che spesso risulta surriscaldato.
Entalpia
La determinazione delle proprietà dei vapori surriscaldati può essere eseguita correlandone le proprietà a quelle del vapore saturo (fig. 2).
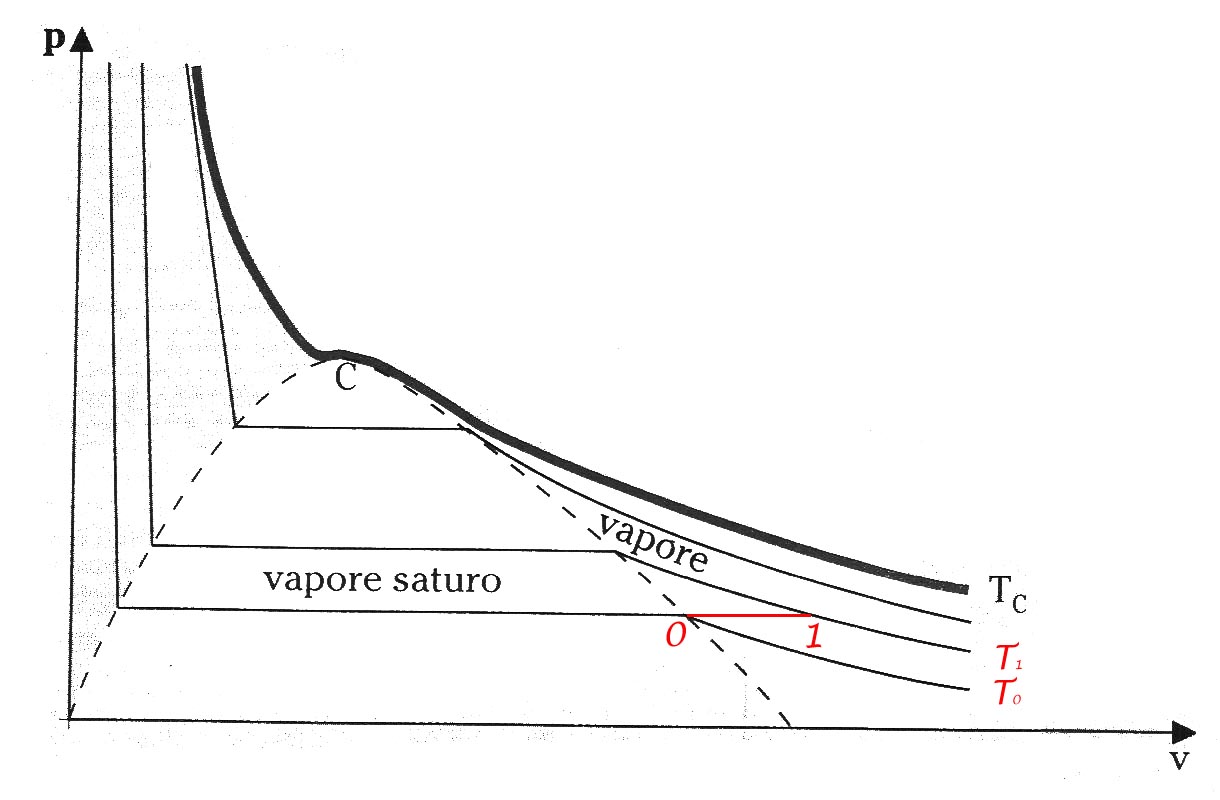
(fig. 2: proprietà vapori surriscaldati)
L'entalpia di un vapore surriscaldato alla pressione p1 ed alla temperatura T1 può essere espressa come somma dell'entalpia del vapore saturo alla pressione p0 (ed alla temperaturaT0) e della variazione di entalpia relativa ad una qualunque trasformazione congiungente i due stati considerati mediante la seguente relazione:
![]() (1)
(1)
Scegliendo come cammino di integrazione l'isobara corrispondente al valore p1 la (1) diventa:
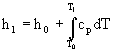 (2)
(2)
Quest'ultima può infine essere riscritta come:
![]() (3)
(3)
Il termine` cp che compare nella (3) è il calore specifico medio e si può calcolare mediante la seguente relazione:
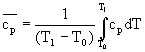 (4)
(4)
Entropia
Per il calcolo dell'entropia si procede in maniera analoga a quanto fatto per l'entalpia:
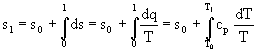 (5)
(5)
Integrando quest'espressione ed introducendo un appropriato calore specifico medio si ottiene:
![]() (6)
(6)
dove il coefficiente cp si calcola attraverso la media logaritmica cosi definita:
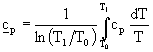 (7)
(7)
A seconda dell'accuratezza più o meno grande richiesta, cp può essere ricavato in vari modi, senza dover necessariamente ricorrere al calcolo di integrali.
Quando la differenza fra gli stati '0' e '1' è piccola, cp può essere considerato quasi costante, per cui non si rende necessario il calcolo della media. Se invece si richiede un minimo di precisione si può ricorrere a delle specifiche tabelle che contengano i valori di` cp (calore specifico medio) validi entro alcuni range di pressione e temperatura. Diversamente se è richiesta una grande accuratezza nei calcoli conviene affidarsi a delle apposite tabelle contenenti i diversi valori di cp al variare della temperatura e della pressione.
Riportiamo qui di seguito una tabella che mette a confronto i valori di cp e` cp relativi al vapore surriscaldato dell'acqua al variare della temperatura e della pressione. Scorrendo i dati si potrà osservare come a parità di pressione e di temperatura la differenza fra i due tipi di dato sia minima.
|
|
Pressione (atm) |
||||||||
|
Temperatura |
1 |
5 |
10 |
20 |
|||||
|
°C |
K |
Calore specifico (kJ/kgK) |
|||||||
|
t |
T |
cp |
` cp |
cp |
` cp |
cp |
` cp |
cp |
` cp |
|
100 |
373.15 |
2.047 |
- |
- |
- |
- |
- |
- |
- |
|
120 |
393.15 |
2.018 |
2.043 |
- |
- |
- |
- |
- |
- |
|
140 |
413.15 |
1.997 |
2.005 |
- |
- |
- |
- |
- |
- |
|
160 |
433.15 |
1.985 |
1.993 |
2.236 |
2.353 |
- |
- |
- |
- |
|
180 |
453.15 |
1.976 |
1.989 |
2.181 |
2.232 |
2.500 |
|
- |
- |
|
200 |
473.15 |
1.980 |
1.985 |
2.139 |
2.177 |
2.361 |
- |
- |
- |
|
220 |
493.15 |
1.985 |
1.980 |
2.106 |
2.152 |
2.278 |
2.370 |
2.943 |
2.851 |
|
240 |
513.15 |
1.989 |
1.980 |
2.085 |
2.139 |
2.223 |
2.328 |
2.667 |
2.734 |
|
260 |
533.15 |
1.997 |
1.985 |
2.077 |
2.131 |
2.190 |
2.294 |
2.495 |
2.621 |
|
280 |
553.15 |
2.005 |
1.989 |
2.072 |
2.127 |
2.169 |
2.278 |
2.382 |
2.567 |
|
300 |
573.15 |
2.014 |
1.989 |
2.072 |
2.123 |
2.152 |
2.261 |
2.328 |
2.525 |
|
320 |
593.15 |
2.026 |
1.993 |
2.077 |
2.119 |
2.144 |
2.244 |
2.290 |
2.487 |
|
340 |
613.15 |
2.039 |
1.993 |
2.281 |
2.110 |
2.139 |
2.232 |
2.261 |
2.453 |
|
360 |
633.15 |
2.047 |
1.997 |
2.085 |
2.110 |
2.135 |
2.219 |
2.240 |
2.424 |
|
380 |
653.15 |
2.060 |
2.001 |
2.093 |
2.110 |
2.135 |
2.211 |
2.227 |
2.399 |
|
400 |
673.15 |
2.072 |
2.005 |
2.102 |
2.106 |
2.139 |
2.206 |
2.215 |
2.378 |
|
420 |
693.15 |
2.085 |
2.014 |
2.110 |
2.106 |
2.144 |
2.198 |
2.211 |
2.361 |
|
440 |
713.15 |
2.098 |
2.018 |
2.119 |
2.110 |
2.148 |
2.194 |
2.206 |
2.349 |
|
460 |
733.15 |
2.110 |
2.022 |
2.131 |
2.110 |
2.156 |
2.194 |
2.211 |
2.340 |
|
480 |
753.15 |
2.123 |
2.026 |
2.244 |
2.110 |
2.165 |
2.190 |
2.211 |
2.332 |
|
500 |
773.15 |
2.135 |
2.031 |
2.152 |
2.114 |
2.173 |
2.190 |
2.215 |
2.324 |
|
520 |
793.15 |
2.148 |
2.039 |
2.165 |
2.114 |
2.186 |
2.190 |
2.219 |
2.315 |
|
540 |
813.15 |
2.165 |
2.043 |
2.177 |
2.119 |
2.194 |
2.190 |
2.227 |
2.311 |
|
560 |
833.15 |
2.177 |
2.047 |
2.190 |
2.123 |
2.206 |
2.190 |
2.236 |
2.307 |
|
580 |
853.15 |
2.190 |
2.056 |
2.202 |
2.127 |
2.215 |
2.190 |
2.244 |
2.303 |
|
600 |
873.15 |
2.202 |
2.060 |
2.215 |
2.127 |
2.227 |
2.194 |
2.252 |
2.299 |
|
620 |
893.15 |
2.215 |
2.064 |
2.227 |
2.135 |
2.240 |
2.194 |
2.261 |
2.299 |
|
640 |
913.15 |
2.227 |
2.272 |
2.240 |
2.139 |
2..252 |
2.198 |
2.273 |
2.294 |
|
660 |
933.15 |
2.244 |
2.077 |
2.257 |
2.144 |
2.265 |
2.198 |
2.286 |
2.294 |
|
680 |
953.15 |
2.257 |
2.085 |
2.269 |
2.148 |
2.278 |
2.202 |
2.299 |
2.294 |
|
700 |
973.15 |
2.269 |
2.089 |
2.282 |
2.152 |
2.290 |
2.206 |
2.311 |
2.294 |
Un modo più rapido di procedere consiste nell'utilizzare delle tabelle a doppia entrata dove al variare di p e di T si trovano tabulati i valori di h, s, v e altre grandezze che possono risultare utili.
La tabella sottostante mostra alcune grandezze caratteristiche del vapor d'acqua surriscaldato nell'intervallo di temperatura compreso fra i 120°C e i 650°C.
|
Pressione |
1,2 bar |
1,4 bar |
1,6 bar |
||||||||||
|
t |
T |
H |
S |
V |
H |
S |
V |
H |
S |
V |
|||
|
°C |
K |
J |
J/K |
m3 |
J |
J/K |
m3 |
J |
J/K |
m3 |
|||
|
120 |
393,15 |
2714,4 |
7,3787 |
1490,1 |
2712,3 |
7,3033 |
1274,0 |
2710,1 |
7,2373 |
1111,9 |
|||
|
140 |
413,15 |
2754,7 |
7,4788 |
1570,8 |
2753,0 |
7,4044 |
1343,7 |
2751,3 |
7,3395 |
1173,4 |
|||
|
160 |
433,15 |
2794,8 |
7,5734 |
1650,5 |
2793,4 |
7,4998 |
1412,5 |
2792,0 |
7,4356 |
1234,0 |
|||
|
180 |
453,15 |
2834,6 |
7,6634 |
1729,7 |
2833,5 |
7,5903 |
1480,7 |
2832,3 |
7,5266 |
1293,9 |
|||
|
200 |
473,15 |
2874,4 |
7,7492 |
1808,4 |
2873,4 |
7,6765 |
1548,4 |
2872,5 |
7,6133 |
1353,4 |
|||
|
220 |
493,15 |
2914,1 |
7,8315 |
1886,7 |
2913,3 |
7,7591 |
1615,7 |
2912,5 |
7,6962 |
1412,5 |
|||
|
240 |
513,15 |
2953,9 |
7,9106 |
1964,7 |
2953,2 |
7,8384 |
1682,8 |
2952,5 |
7,7758 |
1471,3 |
|||
|
260 |
533,15 |
2993,8 |
7,9869 |
2042,6 |
2993,2 |
7,9149 |
1749,7 |
2992,6 |
7,8524 |
1530,0 |
|||
|
280 |
553,15 |
3033,8 |
8,0605 |
2120,3 |
3033,3 |
7,9887 |
1816,4 |
3032,7 |
7,9263 |
1588,5 |
|||
|
300 |
573,15 |
3074,0 |
8,1319 |
2197,9 |
3073,5 |
8,0601 |
1883,0 |
3073,0 |
7,9979 |
1646,8 |
|||
|
350 |
623,15 |
3175,3 |
8,3012 |
2391,5 |
3174,4 |
8,2297 |
2049,1 |
3174,5 |
8,1676 |
1792,3 |
|||
|
400 |
673,15 |
3277,9 |
8,4597 |
2584,7 |
3277,6 |
8,3882 |
2214,9 |
3277,3 |
8,3263 |
1937,5 |
|||
|
450 |
723,15 |
3382,1 |
8,6090 |
2777,7 |
3381,8 |
8,5376 |
2380,4 |
3381,6 |
8,4757 |
2082,4 |
|||
|
500 |
773,15 |
3487,9 |
8,7505 |
2970,6 |
3487,7 |
8,6791 |
2545,8 |
3487,5 |
8,6173 |
2227,3 |
|||
|
550 |
823,15 |
3595,4 |
8,8852 |
3163,4 |
3595,2 |
8,8139 |
2711,1 |
3595,0 |
8,7521 |
2371,9 |
|||
|
600 |
873,15 |
3704,6 |
9,0140 |
3356,1 |
3704,5 |
8,9427 |
2876,4 |
3704,3 |
8,8809 |
2516,6 |
|||
|
650 |
923,15 |
3815,5 |
9,1375 |
3548,7 |
3815,4 |
9,0662 |
3041,5 |
3815.2 |
9,0045 |
2661,1 |
|||
Gli stessi tipi di dati sono inoltre reperibili su degli appositi diagrammi termodinamici. In commercio ve ne sono di vari tipi (pv, Ts, hs) ma quello che può ritenersi più utile è il diagramma di Mollier per l'acqua.
Proprietà dei gas perfetti
Un gas le cui particelle non interagiscano tra loro ed abbiano un proprio volume, trascurabile rispetto al contenitore in cui si trovano, viene definito perfetto. Nel diagramma pv (fig. 3), la regione in cui si trovano i gas perfetti è posta a destra della curva limite superiore, dove la pressione è piccolissima ed il volume specifico grandissimo; qui le isoterme hanno l'andamento di iperboli equilatere.
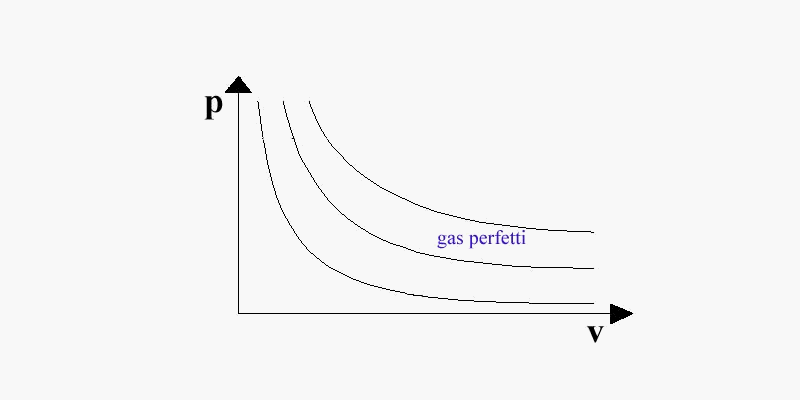
(fig. 3: regione dei gas perfetti )
Attraverso osservazioni sperimentali su sostanze in fase gassosa si è giunti alla formulazione di un'equazione di stato che ne descrive bene l'andamento per valori bassi della pressione:
![]() (8)
(8)
Dove p è la pressione ( Pa ), v è il volume specifico ( m3/kg ) e T è la temperatura ( K ) mentre R è la costante del gas perfetto diversa per ogni tipo di gas. La stessa equazione può essere formulata in altri tre modi a seconda di come si esprimono le grandezze caratteristiche. Ricordando che una mole è una quantità di materia costituita da un numero di Avogadro (6.023× 1023 ), di particelle, e che la massa di una mole è la massa molare M, allora il numero di moli n può essere espresso come rapporto fra la massa molare M e la sua massa molecolare m, cioè :
![]() (9)
(9)
Per cui moltiplicando ambo i membri della (8) per la massa molecolare m, si ottiene:
![]() (10)
(10)
dove vm è il volume specifico molare, mentre R0 è la costante universale dei gas pari a 8315 J/kmolK. La (8) e la (10) possono essere riscritte in termini estensivi moltiplicando la prima per la massa M, e la seconda per il numero di moli n :
![]() (11)
(11)
![]() (12)
(12)
I valori di m ed R, legati dalla relazione R = R0/m, sono riportati, per alcune sostanze, nella seguente tabella.
|
Sostanza |
Formula |
m kg/kmol |
R (J/kgK) |
|
Acetilene |
C2H2 |
26.039 |
319.43 |
|
Acqua |
H2O |
18.016 |
461.70 |
|
Ammoniaca |
NH3 |
17.032 |
488.38 |
|
Anidride carbonica |
CO2 |
44.012 |
188.99 |
|
Anidride solforosa |
SO2 |
64.066 |
129.83 |
|
Argon |
Ar |
39.950 |
208.21 |
|
Aria |
|
28.968 |
287.13 |
|
Azoto |
N2 |
28.014 |
296.91 |
|
Elio |
He |
4.0028 |
2078.0 |
|
Etano |
C2H6 |
30.071 |
276.60 |
|
Etilene |
C2H4 |
28.055 |
296.48 |
|
Freon |
12CCl2F2 |
120.914 |
68.77 |
|
Idrogeno |
H2 |
2.0158 |
4126.4 |
|
Metano |
CH4 |
16.044 |
518.46 |
|
Neon |
Ne |
20.184 |
412.10 |
|
n-Butano |
C4H10 |
58.124 |
143.04 |
|
Ossido di azoto |
NO |
30.007 |
277.19 |
|
Ossido di carbonio |
CO |
28.012 |
296.93 |
|
Ossigeno |
O2 |
31.891 |
260.83 |
|
Propano |
C3H8 |
44.097 |
188.55 |
Come si può notare nella tabella manca la formula dell'aria che a rigore non è chimicamente omogenea; infatti la sua massa molare si può ricavare combinando linearmente le masse dei suoi due principali componenti, azoto e ossigeno, presenti rispettivamente in percentuali del circa 75% e 25%; per cui prendendo i dati dalla tabella si ottiene:
![]() (13)
(13)
Ricaviamo ora le altre caratteristiche termodinamiche dei gas perfetti.
Volume specifico
Il volume specifico si ricava facilmente una volta noti i valori di R, T e p, basta solo sostituirli nella (8) ottenendo cosi:
![]() (14)
(14)
Calori specifici
Si constata facilmente che, per il gas perfetto, anche i calori specifici a pressione e a volume costante dipendono solo dalla temperatura:
![]() (15)
(15)
se nell'espressione di cp della (15) introduciamo il primo principio in forma entalpica si ottiene:
![]() (16)
(16)
poiché stiamo ritenendo costante la pressione, dall'equazione di stato dei gas (8) si può ricavare:
![]() (17)
(17)
sostituendo infine questo risultato nella (16) si ottiene la cosiddetta relazione di Mayer che lega fra loro cp e cv:
![]() (18)
(18)
Moltiplicando ambo i membri della (18) per la massa molecolare m si ottiene:
![]() (19)
(19)
Esiste inoltre un'ulteriore relazione che lega fra loro i calori specifici cp e cv ,e viene chiamato rapporto tra i calori specifici g
![]() (20)
(20)
La teoria cinetica dei gas ha dimostrato come g sia indipendente da cp e cv, ma dipenda invece dai gradi di libertà del sistema, per i gas monoatomici vale 5/3, mentre per i gas biatomici vale 7/5. Sul significato di g ritorneremo in seguito.
Grazie alla (18) e alla (20) siamo ora in grado di ricavare cp e cv, basterà risolvere il seguente sistema algebrico:
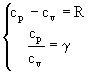 (21)
(21)
La soluzione del sistema (21) può non essere molto precisa, per cui a seconda del grado di accuratezza richiesto è bene consultare la seguente tabella.
In essa sono contenuti i calori specifici medi; questi valori sono impiegabili nell'intervallo 0¸ 100°C, altrove diventano inaccurati.
|
Sostanza |
Formula |
cp kJ/kgk |
cv kJ/kgK |
|
Acetilene |
C2H2 |
1.623 |
|
|
Acqua |
H2O |
0.444 |
|
|
Ammoniaca |
NH3 |
2.218. |
1.766 |
|
Anidride carbonica |
CO2 |
0.865 |
0.676 |
|
Anidride solforosa |
SO2 |
0.607 |
|
|
Aria |
|
1.01 |
0.717 |
|
Azoto |
N2 |
1.04 |
0.743 |
|
Etano |
C2H6 |
1.646 |
|
|
Etilene |
C2H4 |
1.460 |
|
|
Idrogeno |
H2 |
14.2 |
10.1 |
|
Metano |
CH4 |
2.165 |
1.645 |
|
Ossido di azoto |
NO |
0.999 |
|
|
Ossido di carbonio |
CO |
1.04 |
0.743 |
|
Ossigeno |
O2 |
0.917 |
0.656 |
|
Propano |
C3H8 |
1.550 |
|
Energia interna
Per calcolare agevolmente l'energia interna sfruttiamo il fatto che essa è una funzione di stato per cui essa dipenderà dai valori iniziali e finali non dal percorso seguito. Riferendoci alla (fig. 4) consideriamo i punti 1 e 2 posti rispettivamente sulle isoterme T1 e T2 ( T1<T2 ); essi si trovano a una temperatura e a un volume diversi.
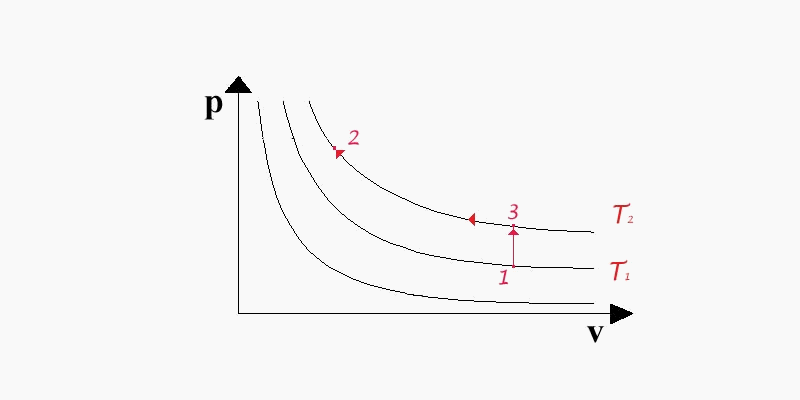
(fig.4: diagramma pv per il calcolo di u)
Per il calcolo della variazione di u utilizzeremo il primo principio della termodinamica:
![]() (22)
(22)
Passiamo in maniera isocora dal punto 1 al punto intermedio 3 che si trova sull'isotermaT2; lungo questo tratto non c'è variazione di volume per cui:
![]() (23)
(23)
ma poiché sappiamo dalla (15) che se v = cost. allora dq = cvdT si ricava:
![]() (24)
(24)
proseguendo con una trasformazione isoterma si giunge allo stato 2; poiché T1=T2 risulterà anche u1=u2 , e sostituendo questa informazione nella (24) si conclude
![]() (25)
(25)
Entalpia
Per quanto concerne il calcolo dell'entalpia si procede in maniera analoga; si considerino gli stati 1 e 2 posti sulle isoterme T1 e T2 come in (fig. 5).
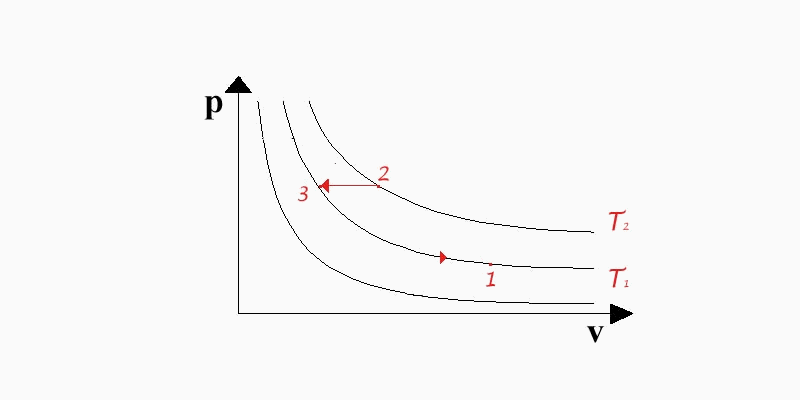
(fig.5: digramma pv per il calcolo di h)
Utilizziamo il primo principio in forma entalpica:
![]() (26)
(26)
Attraverso un tratto di trasformazione isobara passiamo dal punto 2 al punto 3, siccome la pressione p si mantiene costante, allora la (26) diventa:
![]() (27)
(27)
e sempre per il fatto che p = cost. dalla (15) si ha dq = cpdT, quindi:
![]() (28)
(28)
L'ultimo tratto di trasformazione avviene lungo l'isoterma T1 dove non c'è variazione di entropia, per cui h3 = h1 e sostituendo nella (28) infine si ha:
![]() (29)
(29)
Entropia
La variazione di entropia in una trasformazione dallo stato fisico iniziale 1 allo stato fisico finale 2, per un gas perfetto, si può esprimere in due forme diverse (che sono tra loro equivalenti in quanto forniscono lo stesso risultato), a seconda che si utilizzi il primo principio in forma classica o in forma entalpica.
Unendo i risultati della (22) e della (24) si ottiene:
![]() (29)
(29)
a questo punto ricordando la definizione di entropia ne segue:
![]() (30)
(30)
ma poiché stiamo trattando gas perfetti dalla (8) si ricava:
![]() (31)
(31)
ed infine integrando fra gli stati 1 e 2 si perviene a:
![]() (32)
(32)
Partendo dal primo principio in forma entalpica si procede in maniera analoga, basta sfruttare le proprietà (26) e (28) e applicarle alla definizione di entropia:
![]() (33)
(33)
adesso basta soltanto usare la definizione di entropia e ricordare che v/T = R/p :
![]() (34)
(34)
per cui ora integrando fra gli stati 1 e 2 si conclude:
![]() (35)
(35)
I risultati delle (32) e (35) dipendono rispettivamente dalle variazioni delle coordinate vT e pT ; esiste un'ulteriore formulazione della variazione di entropia in funzione delle coordinate pv. Infatti poiché T = pv/R , si ha:
![]() (36)
(36)
E' ancora possibile semplificare questa equazione per via algebrica, sfruttando anche la relazione di Mayer cp - cv = R
![]() (37)
(37)
Dall'espressione del differenziale ds in due forme diverse (ma equivalenti) è possibile determinare una relazione tra le coordinate termodinamiche in una trasformazione isoentropica, cioè adiabatica reversibile. Trattandosi di una trasformazione isoentropica deve essere s = cost., per cui ponendo ds = 0 nelle (32) e (35) si ottiene:
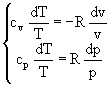 (38)
(38)
Dividendo membro a membro la seconda equazione per la prima, si perviene alla seguente equazione differenziale:
![]() (39)
(39)
Integrando la (39) e introducendo una costante di integrazione k si ottiene:
![]() (40)
(40)
Per cui passando dai logaritmi all'argomento dei logaritmi , infine ci fornisce:
![]() (41)
(41)
Tale equazione, detta di Poisson, rappresenta la trasformazione isoentropica per i gas perfetti; nel digramma pv (fig.6) è una curva monotona decrescente, con una pendenza maggiore dell'isoterma.
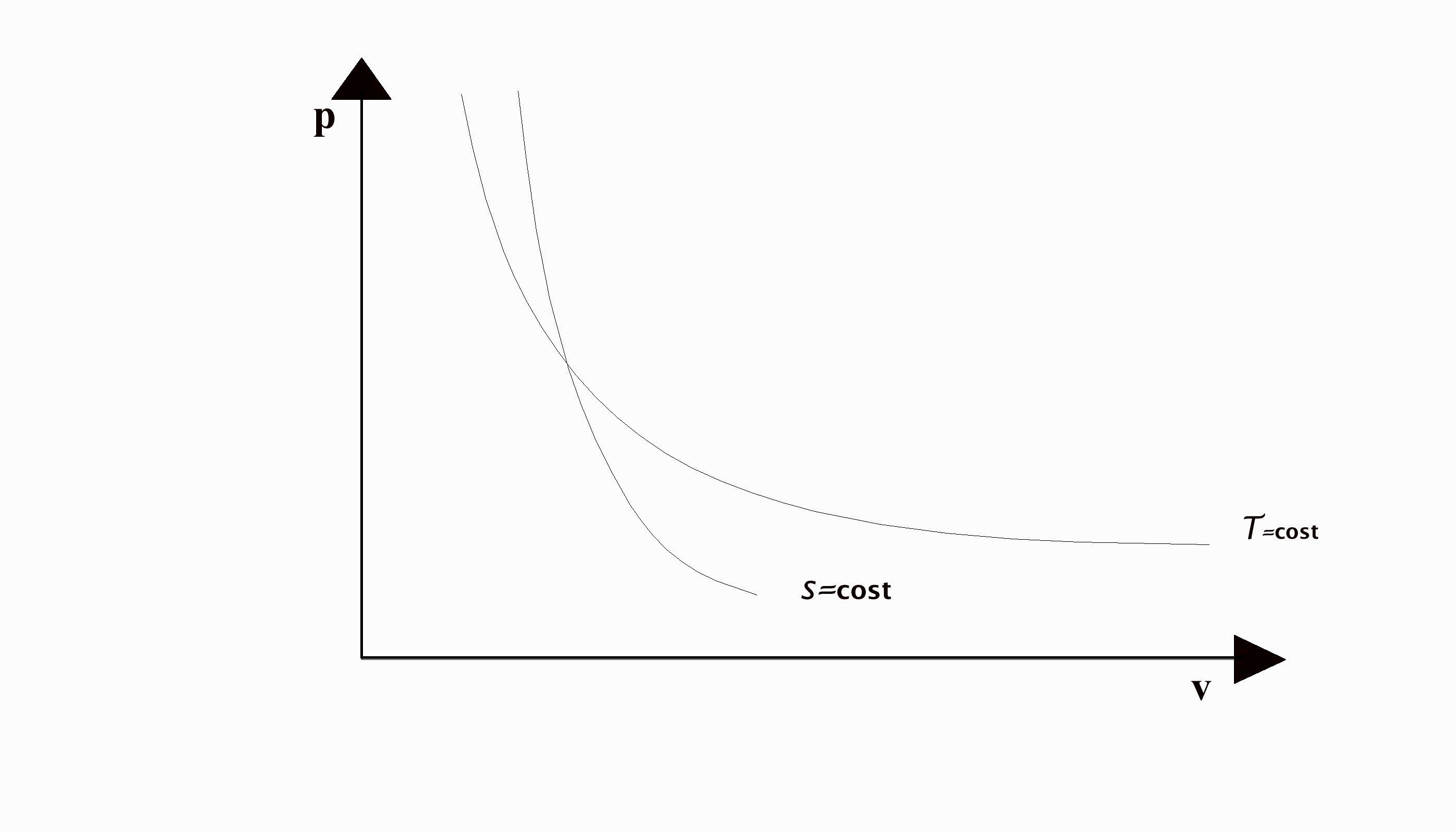
(fig.6: confronto isoterma adiabatica)
Dalla (41) si possono dedurre altre due equazioni che rappresentano la stessa trasformazione isoentropica però in funzione di pT e Tv; infatti usando l'equazione di stato dei gas perfetti si ha:
![]() (42)
(42)
![]() (43)
(43)
Proprietà dei gas reali
La relazione fondamentale che caratterizza un gas perfetto è la sua equazione di stato. I gas reali obbediscono all'equazione di stato solo in condizioni di bassa pressione e generalmente di alta temperatura, per cui le deviazioni dal comportamento ideale sono tanto più rilevanti quanto più ci si allontana dalla rarefazione del gas andando verso la condensazione. Infatti il prodotto pv all'aumentare della pressione non solo non è costante, ma la sua dipendenza dalla pressione è influenzata in modo rilevante dalla temperatura.
Moltissime equazioni di forma più o meno complicata sono state proposte come equazioni di stato per i gas reali; alcune di queste sono frutto di teorie che si è dimostrato essere sbagliate, o perlomeno potevano essere applicate solo in campi molto ristretti.
Van der Walls ricavò un'equazione di stato che teneva conto dei fattori che differenziano un gas reale da quello ideale.
![]() (44)
(44)
Questa equazione contiene però dei parametri caratteristici della particolare natura del fluido, per cui senza questi è inutilizzabile.
Se invece si introducono le coordinate in forma ridotta, definite come
![]() (45)
(45)
essendo pc ,vc e Tc i parametri termodinamici al punto critico, è poi possibile esprimere con un solo parametro lo scostamento del comportamento di un gas ideale da quello reale. Si definisce allora un fattore in funzione delle coordinate ridotte detto fattore di compressibilità z, ricavabile dalla relazione
![]() (46)
(46)
Dove zc è un valore diverso per ogni gas e si ottiene da
![]() (47)
(47)
.Noto il fattore di compressibilità si può scrivere un'equazione di stato del tipo:
![]() (48)
(48)
Riportiamo qui di seguito una tabella contenente i parametrici critici di alcune sostanze di uso comune.
|
Sostanza |
Formula |
Tc K |
pc× 10-5 Pa |
vc× 103 m3/kg |
zc |
|
Acetilene |
C2H2 |
309.5 |
62.4 |
4.33 |
0.274 |
|
Acqua |
H2O |
647.3 |
221.1 |
3.11 |
0.230 |
|
Ammoniaca |
NH3 |
405.4 |
112.8 |
4.26 |
0.243 |
|
Anidride carbonica |
CO2 |
304.2 |
73.9 |
2.13 |
0.275 |
|
Anidride solforosa |
SO2 |
430.7 |
78.8 |
1.92 |
0.269 |
|
Argon |
Ar |
150.9 |
48.9 |
1.87 |
0.291 |
|
Aria |
|
132.4 |
37.7 |
3.22 |
0.319 |
|
Azoto |
N2 |
126.2 |
33.9 |
3.21 |
0.291 |
|
Elio |
He |
5.2 |
2.3 |
14.5 |
0.308 |
|
Etano |
C2H6 |
305.4 |
48.8 |
4.92 |
0.285 |
|
Etilene |
C2H4 |
283.1 |
51.2 |
4.42 |
0.270 |
|
Freon |
12CCl2F2 |
385.2 |
41.1 |
1.79 |
0.279 |
|
Idrogeno |
H2 |
33.2 |
13.0 |
32.5 |
0.304 |
|
Metano |
CH4 |
190.7 |
46.4 |
6.17 |
0.290 |
|
Neon |
Ne |
44.4 |
27.3 |
2.07 |
0.308 |
|
n-Butano |
C4H10 |
425.2 |
38.0 |
4.39 |
0.274 |
|
Ossido di azoto |
NO |
179.2 |
65.9 |
1.93 |
0.256 |
|
Ossido di carbonio |
CO |
132.9 |
35.0 |
3.32 |
0.294 |
|
Ossigeno |
O2 |
154.8 |
50.8 |
2.31 |
0.292 |
|
Propano |
C3H8 |
370.0 |
42.7 |
4.53 |
0.277 |
Applicazione: lo scatolone adiabatico
Consideriamo uno scatolone come in figura, che ha le pareti coibentate in modo da non poter scambiare calore con l'esterno. Al suo interno presenta due vani, che chiameremo 1 e 2, separati da un setto rimovibile che non consente lo scambio né di lavoro né di calore. In entrambi i vani c'è dell'aria, che supponiamo essere un sistema chimicamente puro, in quantità e condizioni termodinamiche diverse. In un secondo tempo il setto viene rimosso per cui si raggiunge un nuovo stato di equilibrio che chiameremo3. Ci proponiamo di ricavare le condizioni finali.

I dati e le incognite del problema sono i seguenti:
1 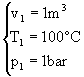 2
2 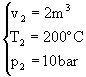 3
3 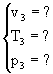
Prima di iniziare a risolvere il problema facciamo alcune considerazione che ci faciliteranno il lavoro:
-il processo di unione dei due vani è ovviamente irreversibile;
-poiché abbiamo considerato l'aria un sistema chimicamente puro, nello stato 3 avremo ancora aria;
-il sistema è termicamente e meccanicamente isolato quindi l'energia interna dello stato iniziale e finale coinciderannoÞ u3 = u1+u2;
-poiché il sistema è chiuso si conserva anche la massaÞ M3 = M1+M2.
Da queste considerazioni si capisce subito che v3 è dato dalla somma di v1 e v2, per cui le vere incognite cono T3 e p3. Abbiamo dunque bisogno di due equazioni indipendenti per risolvere questo problema in due incognite. Possiamo sfruttare la conservazione dell'energia e la conservazione della massa.
Le masse si possono ricavare dall'equazione dei gas perfetti (11), per cui, convertendo i dati in unità S.I., si ha
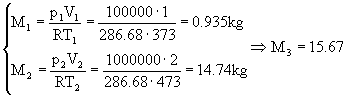 (49)
(49)
La conservazione dell'energia può essere espressa mediante la (25), indicando con t le differenze di temperatura
![]() (50)
(50)
ricordando che cv1 = cv2 = cv3, semplificando la (50) ricavo t3
![]() (51)
(51)
Per cui adesso non resta che determinare p3
![]() (52)
(52)
Per avere un quadro completo e concludere possiamo calcolare l'aumento di entropia dell'universo; infatti un aumento ci sarà stato sicuramente dal momento che la trasformazione è di tipo irreversibile. Poiché l'entropia è una funzione di stato non è necessario fare un'analisi approfondita della trasformazione verificatasi, ma basta conoscere gli stati iniziali e finali:
![]() (53)
(53)
Ora basta fare solo dei semplici calcoli utilizzando le formule ricavate prima. Fissate le condizioni iniziali di riferimento, che per noi saranno: T0 =273K, p0 =1bar; noti i valori di R e cp per l'aria, sostituendo si ha:
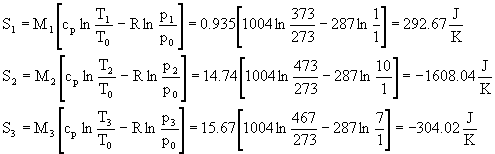
![]()
Dunque tirando le somme si ha che la variazione di entropia è:
![]()
cioè nell'universo c'è un aumento di entropia, in accordo con le nostre ipotesi.