I PRINCIPIO DELLA TERMODINAMICA
Lezione del 3.10.2000, ore 16.30 - 18.30
Trascritta da Facen Alessio - matr. 124951
Definizioni e convenzioni
Primo principio per sistemi chiusi
Esperienza di Joule
Stato fisico di un sistema. Legge di Gibbs
Primo principio nelle forme specifica e differenziale
Entalpia
Il primo principio della termodinamica è l'espressione del concetto filosofico "L'energia non si crea e non si distrugge", quindi è un'enunciazione della legge di conservazione
dell'energia. Tale principio è completato dalla legge di equivalenza massa-energia formulato da A. Einstein (E=mc2), che lo rende valido anche in situazioni in cui a prima vista
sembra che delle energie compaiano o scompaiano dal nulla, mentre in realtà sono trasformazioni da o in massa.
Si vuole introdurre la definizione di sistema termodinamico, che può essere formulata in due modi:
 |
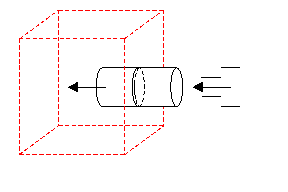
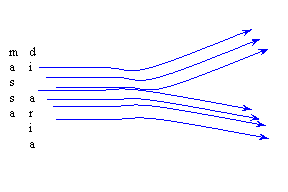
 | fig. 1 - esempio di sistema aperto | fig. 2 - esempio di sistema chiuso |
A seconda di quale dei due concetti si voglia adottare per descrivere il sistema fisico che si desidera esaminare, si applicano principi e leggi differenti: esistono infatti una termodinamica
dei sistemi chiusi ed una termodinamica dei sistemi aperti. Ovviamente, bisogna che almeno una delle due definizioni possa essere presa in considerazione; d'altro canto, esse non sono mutuamente esclusive. Così
esistono sistemi aperti (ad esempio il serbatoio del carburante di un'automobile), sistemi chiusi (come una pinta di birra che si disperde dopo essere stata versata in un fiume), sistemi sia aperti che chiusi (una
contenitore di gas chiuso ermeticamente) ed oggetti fisici che non possono venire classificati come sistema termodinamico (come in un motore a scoppio, nel quale la zona dove entra ed esce il carburante subisce
delle variazioni di volume).
Nella trattazione seguente, si farà riferimento a sistemi chiusi.
Una volta definito il concetto di sistema, si può introdurre il suo complementare, ovverosia l'ambiente, semplicemente come insieme di ciò che non appartiene al sistema.
L'unione di ambiente e sistema viene chiamato universo, ed è ad esso che fa riferimento l'enunciato del primo principio della termodinamica.
Inoltre, le proprietà del sistema vengono esaminate esclusivamente in due istanti separati, il "prima" e il "dopo" del processo, senza curarsi di ciò che avviene tra di essi: l'analisi degli eventi intercorrenti dall'istante iniziale a quello finale dell'eventuale trasformazione non hanno alcuna rilevanza ai fini di questo tipo di studio (infatti, si parla di "termodinamica dei sistemi e degli stati", che è solo una piccola parte della termodinamica intesa in senso generale).
Prendendo in considerazione sistemi chiusi, si nota come l'involucro iniziale del sistema sia - oltre che deformabile - impermeabile al passaggio della materia ma non dell'energia, che può
fluire o defluire liberamente in o da esso sotto varie forme, quali ad esempio radiazioni elettromagnetiche o vibrazioni meccaniche. Tuttavia, per lo studio dei fenomeni termodinamici, i trasferimenti di energia tra sistema ed
ambiente vengono fondamentalmente ricondotti a due categorie: il lavoro (come ad esempio nella deformazione della superficie, o nell'azione di macchine elettriche) ed il calore (come quello fornito dalle onde
elettromagnetiche o dalla vibrazione molecolare).
Nella trattazione di tali quantità di energia, si adotta la seguente convenzione:
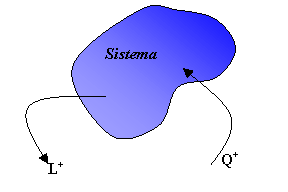
fig. 3 - convenzioni sui segni di lavoro e calore
Primo principio per sistemi chiusi
Sia dato un sistema termodinamico chiuso, dotato di una certa energia iniziale E1 (che può essere di tipo chimico, potenziale gravitazionale, potenziale elettrico...); sia inoltre E2 l'energia finale del sistema. Allora si ha che
(1) ![]()
Ovvero, l'eventuale incremento di energia di un sistema termodinamico è dato dalla differenza tra il calore acquisito e il lavoro compiuto dal sistema stesso.
Si può notare come dell'energia del sistema E facciano parte due classi:
Si definisce quindi l'energia interna del sistema come energia diversa dalle due forme sopra menzionate:
(2) ![]()
Rispetto a quella interna, si può considerare trascurabile il contributo dell'energia cinetica e di quella potenziale; inoltre, supponendo che il sistema rimanga fermo, la variazione di queste ultime è nulla. Pertanto dell'energia totale l'unica componente che subisce delle mutazioni durante il processo è quella interna; si arriva quindi a scrivere la forma più utilizzata del primo principio:
(3) ![]()
J.P. Joule (1818 - 1889) nel 1843 dimostrò sperimentalmente come la variazione di energia interna di un sistema fosse indipendente dal processo seguito.
L'esperimento consisteva nel comprimere ed espandere in varie maniere del gas tramite un pistone, portandolo da uno stadio iniziale ad uno finale comune a tutte le trasformazioni, e misurandone
i parametri come la temperatura e la pressione.
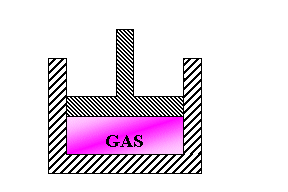 |
 | fig. 4 - dispositivo usato da Joule | fig. 5 - esempi di possibili processi esaminati |
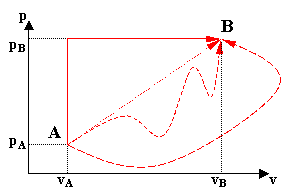
A seguito delle numerose osservazioni compiute, Joule notificò che la differenza tra il calore fornito al sistema e il lavoro che esso compiva sul pistone - ovvero la variazione di energia interna - rimaneva costante indipendentemente da come il processo si era evoluto:
(4) ![]()
Stato fisico di un sistema. Legge di Gibbs
Si definisce lo stato fisico di un sistema come l'insieme, in genere di cardinalità abbastanza ridotta, di grandezze fisiche necessarie a descrivere totalmente e compiutamente il sistema stesso. Tuttavia, questa definizione è valida solamente se tutta la materia del sistema è grossomodo nelle stesse condizioni, ovvero se le proprietà di un punto sono verificate in tutti gli altri.
Una grandezza fisica è detta funzione di stato se il suo valore numerico non dipende direttamente da eventi passati, ma è funzione unicamente dello stato del sistema.
Non sono funzioni di stato in particolare le variabili fisiche il cui valore dipende dal cammino percorso, come ad esempio il calore o il lavoro.
Materialmente, si può dire che è una funzione di stato ciò che si può esprimere con una formula dipendente esclusivamente dalle grandezze fondamentali che descrivono lo stato fisico
del sistema; ad esempio, l'esperienza di Joule dimostra che la variazione di energia interna DU è una funzione di stato. Questo porta anche ad una seconda formulazione del primo
principio della termodinamica, riferendosi a sistemi ciclici (per cui la differenza di energia interna, partendo e tornando allo stesso stato, è nulla): non è possibile costruire un
perpetuum mobile di prima specie, ovvero una macchina termodinamica a funzionamento ciclico che svolga una quantità di lavoro superiore alla quantità di calore ricevuta dall'esterno.
Si evidenzia il fatto che solamente le funzioni di stato sono grandezze differenziabili: quindi è perfettamente lecito indicare una variazione infinitesima dell'energia interna del sistema con il simbolo dU.
Invece, matematicamente è errato considerare oggetti come dQ o dL come differenziali esatti: infatti, come già specificato, tali grandezze sono dipendenti dal cammino seguito,
ed un'operazione di integrazione porterebbe ad avere risultati differenti a seconda di esso. Pertanto, per indicare la non esattezza di tali differenziali, si utilizzano i simboli ðQ e ðL, e
ci si riferisce ad essi come a variazioni molto piccole di calore e lavoro.
A questo è evidente la necessità di conoscere quale sia il numero minimo di variabili indipendenti utili a descrivere lo stato di un sistema. La risposta a questo quesito è data dalla legge di Gibbs, anche conosciuta come "regola delle fasi":
(5) ![]()
dove n è il numero di specie chimiche indipendenti presenti, f è il numero di fasi (solide, liquide o gassose) presenti e v è il grado di varianza del sistema.
La legge, enunciata da J.W. Gibbs (1839 - 1903) nel 1896, serve per stabilire quante variabili fisiche indipendenti possono essere modificate in un sistema termodinamico senza alterarne l'equilibrio - ovvero, quante grandezze fisiche sono utili a caratterizzare il sistema, anche se espressa così la regola in realtà non è esatta, poiché per sistemi chiusi il numero di variabili indipendenti è comunque 2.
Ad esempio, se si considera un sistema costituito da una certa quantità di gas perfetto, dalla formula (5) si ha che
![]()
quindi ci sono due variabili indipendenti (potrebbero essere pressione e temperatura).
Se invece si considera un sistema formato da acqua e ghiaccio in equilibrio, si ha
![]()
Il significato della monovarianza sta nel fatto che per ogni temperatura esiste un'unica pressione alla quale il sistema sia in equilibrio. In realtà, bisognerebbe conoscere anche la massa di ghiaccio, o di acqua, rispetto a quella totale (quindi le grandezze che descrivono il sistema sono due).
Se si osserva il caso limite, ovvero quello di una sostanza al punto triplo (stato in cui coesistono in equilibrio la fase solida, la fase liquida e la fase gassosa di un elemento puro), si nota che
![]()
Infatti, il punto triplo di una sostanza è unico e fissato a certi valori (ad esempio, il punto triplo dell'acqua si ha per una temperatura di 273.16 K e ad una pressione di 610.66 Pa, mentre quello dell'anidride carbonica a 215.15 K e 516750 Pa). Peraltro, per sistemi chiusi si ha la necessità di conoscere il rapporto tra la massa di almeno due delle fasi della sostanza e quella totale, ritrovando ancora le due grandezze utili.
Nel caso di leghe metalliche o di soluzioni liquide non miscibili tra loro, il conteggio del numero delle fasi viene effettuato per ogni singola specie (così ci possono essere ad esempio due fasi liquide in una soluzione acqua - propano), mentre la fase gassosa è sempre unica anche in miscele di gas diversi.
Primo principio nelle forme specifica e differenziale
Nella trattazione di sistemi chiusi, è utile introdurre i concetti di grandezze estensive ed intensive. Nel primo caso, allorché si aumenta la massa del sistema si osserva una variazione proporzionale della grandezza in questione; nel secondo caso, il valore della variabile non è influenzato dalla massa. Ad esempio, sono grandezze estensive il volume e l'energia interna, mentre sono intensive la temperatura e la pressione.
Dividendo una grandezza estensiva per l'unità di massa, si ottiene una grandezza intensiva detta grandezza specifica (quali il volume specifico o l'energia interna specifica), che viene indicata
con la stessa lettera della grandezza originaria in minuscolo (per esempio, il volume specifico v). Ovviamente l'unità di misura viene quindi divisa per quella della massa, ovvero il kg nel sistema internazionale: ad esempio,
l'energia interna specifico si misura in J / kg (sempre nel SI).
Per sistemi chiusi, dato che la massa del sistema per definizione è costante, è possibile dividere relazioni ed equazioni per la massa stessa, ottenendone così delle altre indipendenti da essa. Così, il primo principio in forma specifica diventa
(6) ![]()
Si suppone ora di considerare una variazione infinitesima di stato. Poiché come già verificato l'energia interna è una funzione di stato e quindi differenziabile, si può riscrivere il primo principio come
(7) ![]()
che è una forma matematicamente corretta; però, sebbene l'operazione di distribuzione del differenziale al secondo membro non sia ammissibile (dato che Q e L non sono grandezze differenziabili) si esprime il primo principio della termodinamica in forma differenziale come
(8) ![]()
oppure (in forma specifica)
(9) ![]()
Poiché i differenziali di lavoro e calore non sono esatti, formalmente l'espressione è errata: infatti, integrando il secondo membro non si otterrebbe un valore indipendente dal percorso svolto, come evidenziato in figura 6.
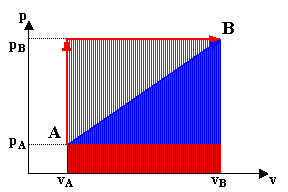
fig. 6 - nel passaggio da A a B, le aree sottese ai due processi (rosso e blu)
rappresentano il lavoro compiuto (vedi eq. 16) da essi, e si nota
come queste siano differenti a seconda del cammino seguito.
Però si suppone di poter effettuare l'operazione, scegliendo precedentemente il cammino e riferendosi a quello sia per il lavoro che per il calore. Per semplicità, quindi, d'ora in poi verranno utilizzati i simboli dQ, dL, dq e dl pur non essendo formalmente corretti.
E' possibile a questo punto dare la definizione del calore specifico:
(10) ![]()
![]()
che al solito dipende dal percorso seguito. Si considerano quindi due casi importanti: quello a pressione costante (per trasformazioni isobare):
(11) 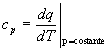
e quello a volume costante (per processi isocori):
(12) 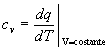
Il calore specifico non è costante, ma cambia a seconda della temperatura. D'altra parte per semplicità si suppone di poter trascurare tale variazione in intervalli di temperatura di ampiezza
relativamente elevata: ad esempio, il calore specifico dell'acqua può ragionevolmente essere considerato costante nell'intervallo tra il punto di solidificazione (273.16 K) ed il punto di ebollizione (373.16 K).
Per quanto riguarda i solidi ed i liquidi, in genere viene utilizzato un solo valore indipendente dal processo seguito; la distinzione invece è molto più importante per le sostanze allo stato gassoso. Segue una tabella contenente alcuni valori di cv e cp, misurati - se non altrimenti specificato - a temperatura ambiente.
|
Sostanza |
cv (kJ/kgK) |
cp (kJ/kgK) |
|
|
||
|
Elio |
5.2325 |
3.1521 |
|
Argon |
0.5232 |
0.3139 |
|
Idrogeno |
14.1905 |
10.0464 |
|
Monossido di carbonio |
1.0381 |
0.7367 |
|
Anidride carbonica |
0.8330 |
0.6363 |
|
Aria (a 373 K) |
1.0046 |
0.7200 |
|
Vapore acqueo (a 373 K) |
2.0177 |
1.3563 |
|
|
||
|
Alcool etilico |
2.4279 |
|
|
Benzina |
1.5070 |
|
|
Acqua |
4.1860 |
|
|
Etere etilico |
2.3023 |
|
|
Glicerina |
2.3860 |
|
|
Mercurio |
0.1381 |
|
|
|
||
|
Alluminio |
0.8958 |
|
|
Argento |
0.2344 |
|
|
Rame |
0.3851 |
|
|
Diamante |
0.5023 |
|
|
Stagno |
0.2302 |
|
|
Ferro |
0.4605 |
|
|
Oro |
0.1466 |
|
|
Piombo |
0.1256 |
|
|
Quarzo |
0.7032 |
|
|
Vetro |
0.8372 |
|
|
Zolfo |
0.7451 |
|
|
Zinco |
0.3893 |
|
Sostituendo il termine dq nell'espressione del primo principio con quello ricavabile dalla (10), si trova
(13) ![]()
Considerando ora il caso del pistone che comprime ed espande un gas, si definisce come "lavoro" unicamente la deformazione dell'involucro del sistema tramite lo spostamento del pistone stesso.
Siano A l'area di base del pistone, F la forza impressa da questo al gas e z la coordinata dell'altezza del cilindro nel quale il gas è contenuto. Con 1 e 2 si contrassegnano rispettivamente lo stato iniziale e quello finale del processo.
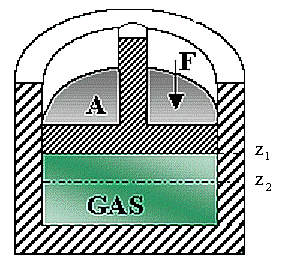
fig. 7 - sezione del sistema cilindro-pistone
Poiché non è noto il comportamento della forza al variare del cammino, l'espressione del lavoro viene data in forma integrale:
(14) ![]()
Moltiplicando e dividendo per l'area del pistone, e sfruttando le relazioni tra forza e pressione e tra altezza e volume, si ottiene:
(15) ![]()
dove nell'ultima equivalenza si è raccolta la massa del sistema, che è costante, facendo comparire il differenziale del volume specifico. Pertanto, dividendo per la massa e differenziando ambo i membri, si ottiene
(16) ![]()
Questa relazione può essere sostituita quindi nell'espressione del primo principio:
(17) ![]()
In particolare, se si considera un processo isocoro come in fig.8, il termine pdv dà contributo nullo e quindi integrando la (17) si ottiene
(18) ![]()
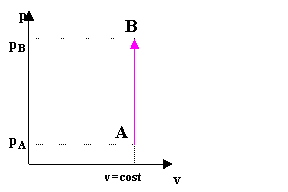
fig. 8 - esempio di processo isocoro
Per un gas perfetto, il calore specifico è costante ed indipendente dalla temperatura: in questo caso, si ha quindi
(19) ![]()
Ergo l'incremento di energia interna di un gas perfetto è unicamente funzione del suo aumento di temperatura in qualsiasi processo, perché come già detto DU è funzione di stato. Si può estendere il concetto, fissando una temperatura di riferimento cui assegnare per convenzione un valore di energia specifica nullo (ad esempio, a 273 K) in modo da potere parlare di energia interna "assoluta" in relazione ad essa: ad esempio, si può dire che
![]()
e che l'energia interna di un gas perfetto è unicamente funzione della sua temperatura. In questo caso, quindi, anche U diventa funzione di stato.
Si definisce l'entalpia, una grandezza di stato che esprime la quantità di energia che il sistema può scambiare con l'esterno:
(20) ![]()
![]()
o in forma specifica
(21) ![]()
![]()
Differenziando quest'ultima relazione, si ha
(22) ![]()
Ricavando du e sostituendo l'espressione trovata nel primo principio,
(23) ![]()
da cui, semplificando il pdv, si trova il primo principio della termodinamica per sistemi chiusi in forma entalpica:
(24) ![]()
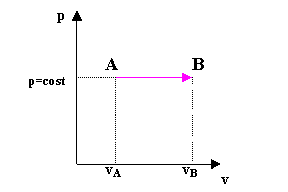
fig. 9 - esempio di processo isobaro
In particolare, se si considera un processo isobaro (come in fig. 9) il termine vdp è nullo, ed integrando si trova
(25) ![]()
dove l'ultimo passaggio è valido solo se il calore specifico è indipendente dalla temperatura (come ad esempio in un gas perfetto).
Come per l'energia interna, anche per l'entalpia si può instaurare una convenzione di riferimento; in questo caso, si può parlare anche di entalpia "assoluta" in relazione a tale valore:
![]()
in questo caso il riferimento è stato preso per h=0 ad una temperatura di 273.15 K.