Il primo principio della termodinamica ha due conseguenze storiche e scientifiche fondamentali:

1. elimina definitivamente il concetto fuorviante di "calorico", ossia quel fluido indistruttibile e imponderabile che transita dai corpi caldi a quelli freddi.
2. stabilisce che il calore, come il lavoro, è una forma di energia.

Tuttavia, partendo da questo assunto, si è portati a pensare che tutte le forme di energia siano intercambiabili e, in particolare, che anche il calore possa essere convertito indiscriminatamente in lavoro.

Se questo fosse vero, date le molte fonti di calore inesauribili esistenti in natura, non si avrebbe difficoltà a trasformarle in lavoro e il problema sarebbe risolto.

In realtà, si può fare una classificazione delle varie forme di energia, stabilendo una vera e propria gerarchia:

• Classe A: sono le forme di energia nobili come lavoro meccanico ed energia elettrica. Rientrano in questa categoria anche le forme di energia chimica che possono essere convertite con rendimenti alti in lavoro meccanico o elettrico mediante un processo elettrochimico (es. pile o batterie).In tutti questi casi, l’entità della perdita è piccola e perfettibile all’infinito rallentando il processo ed eliminando i fattori dissipativi: teoricamente non esiste un limite alla riduzione delle perdite.
• Classe B: sono le forme di energia degradata, che hanno una bassa capacità di conversione, come calore ed energia chimica non convertibile in lavoro elettrico o meccanico, ma trasformabile in calore mediante processi di combustione (es. combustione di carbone, benzina, gas naturale).

Mentre si può sempre andare da A a B, il percorso inverso è impedito a meno di una grossa percentuale discreta e finita, che rappresenta un limite invalicabile.

Come esempio consideriamo un recipiente contenente 100 litri di acqua calda alla temperatura T = 100°C, mentre l’ambiente è a T₀ = 20°C. Ci chiediamo quanto calore può erogare il sistema all’ambiente esterno, fino a portarsi a T₀.

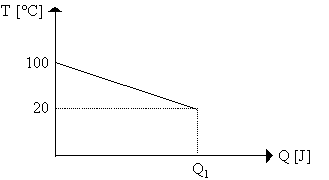
Fig. 1

Q₁ = M * c_p * (T₁-T₂) = 100 * 4187 * 80 = 33496000 J

Se questo calore fosse convertibile in lavoro, basterebbe una risorsa di energia termica come l’acqua calda per far funzionare le automobili!

In realtà, tanto maggiore è la temperatura del sistema, tanto più elevato è il grado di convertibilità dell’energia in lavoro, ma esiste sempre un limite, stabilito dal secondo principio della termodinamica.

E’ utile introdurre due concetti che saranno utili in seguito per la formulazione del secondo principio:

• exergia: energia convertibile
• anergia: energia non convertibile

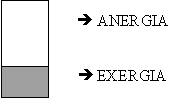
Fig. 2

Filosoficamente, questi due termini hanno assunto i significati di "energia buona" ed "energia cattiva", ma tale contrapposizione non ha senso perché anche l’anergia può essere utile (riscaldamento domestico), mentre l’exergia può essere dannosa.

Non si può nemmeno pensare di diminuire al massimo le perdite di exergia per conservare l’equilibrio ecologico, perché è la natura stessa che provvede a creare continuamente anergia e distribuire exergia.

Come esempio, si consideri una pila carica: essa contiene energia nobile, ma se la colleghiamo ad una resistenza, si dissipa energia per effetto Joule (calore). In pratica siamo partiti da una situazione iniziale di totale exergia per arrivare ad una situazione finale in cui abbiamo molta anergia e poca exergia: l’energia totale non è cambiata ma è degradata. Sarebbe stato meglio, a tal proposito, ricavare calore da energia chimica già degradata (ad es. dalla combustione del carbone).

In Italia, secondo il Piano Energetico Nazionale, si usa energia nobile per il riscaldamento degli edifici, energia che alla fine ha un contenuto exergetico basso, dal momento che le temperature raggiunte sono sempre di poche decine di gradi centigradi. Sarebbe più conveniente utilizzare l’exergia delle categorie nobili di energia per produrre energia elettrica, quindi usare la quota di anergia necessaria per il riscaldamento degli edifici civili.

Per introdurre correttamente il secondo principio abbiamo bisogno di due definizioni preliminari:

1. serbatoio di calore
1. macchina ciclica

Vediamoli in dettaglio:

1. serbatoio di calore: sistema chiuso che scambia con l’ambiente circostante quantità di calore positive o negative grandi a piacere, senza variare la sua temperatura.

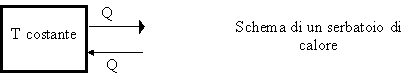
Fig. 3

 Il fulcro di questa definizione sta nel significato di "grandi a piacere". Se avessi un sistema con un volume grande, al limite infinito, avrei un serbatoio perfetto, mentre un sistema con volume finito e fisso pone sempre un limite alla quantità di calore scambiato.

E’ chiaro che il serbatoio di calore è un concetto astratto, al quale ci si può avvicinare asintoticamente attraverso opportuni accorgimenti.

Un classico esempio, facilmente realizzabile, è il serbatoio di calore a freddo, costituito da un recipiente con all’interno un bagno di acqua liquida e ghiaccio a 0°C e alla pressione di 1 BAR. Possiamo fornire calore, e ottenere la fusione di una percentuale di ghiaccio, oppure raffreddare il sistema e far solidificare una certa quantità d’acqua, mantenendo costante la temperatura.

Un altro esempio è costituito dal serbatoio di calore a caldo, ossia un recipiente contenente acqua liquida e vapore acqueo a 100°C e alla pressione di 1 BAR, al quale aggiungiamo e togliamo calore restando alla temperatura fissata.

Di solito, si considera un grande serbatoio di calore l’ambiente naturale: infatti, la temperatura delle masse d’acqua di mari, laghi e fiumi si mantiene pressoché costante anche con scambi di notevoli quantità di calore.

2. Macchina ciclica: macchina a fluido che, al termine di un processo, torna allo stato fisico di partenza. Quindi la sua variazione di energia interna è zero: D U = 0.

Essa scambia calore tra due serbatoi a temperatura costante (ma diversa tra loro) e passa con continuità da uno stato all’altro mediante trasformazioni quasi - statiche.

Alcuni esempi sono: la pompa della bicicletta, il motore a scoppio, il motore diesel, il ciclo a vapore delle caldaie o delle turbine nelle navi.

Una macchina a fluido può essere un sistema aperto o chiuso, ad esempio la macchina a vapore è un sistema chiuso (l’acqua è sempre la stessa), il motore a combustione interna è un sistema aperto (brucia benzina ed emette gas).

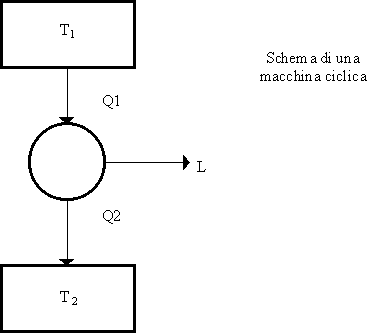
Fig. 4

Vediamo ora le formulazioni del secondo principio della termodinamica:

Enunciato di Kelvin - Planck: non è possibile effettuare una trasformazione il cui unico risultato sia la conversione di calore in lavoro.

Questo enunciato stabilisce che non è possibile costruire una macchina che operi una conversione del calore in lavoro mediante un unico serbatoio caldo, senza cedere calore ad un serbatoio freddo. Quindi lo schema seguente non è realizzabile:

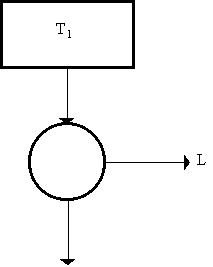
Fig. 5

Il significato fondamentale dell’enunciato di Kelvin - Planck risiede nelle parole "il cui unico risultato".

Ad esempio, si pensi di fornire una certa quantità di calore ad un sistema, che contemporaneamente diminuisce la propria pressione e aumenta il proprio volume secondo una legge tale da mantenere costante il contenuto energetico del sistema stesso.

Dal primo principio, si ha che il lavoro ottenuto è uguale al calore fornito, però questo non è l’unico risultato della trasformazione perché il volume finale del sistema risulta superiore a quello iniziale: lo stato fisico del sistema è cambiato.

Enunciato di Clausius: non è possibile effettuare una trasformazione il cui unico risultato sia il passaggio di calore da un serbatoio freddo ad uno caldo.

Questo enunciato fa riferimento al principio zero della termodinamica, secondo il quale il calore passa spontaneamente da un corpo caldo ad uno freddo.

Lo schema seguente non è quindi realizzabile:

T₁ > T₂

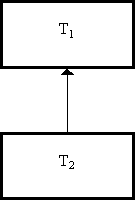
Fig. 6

Anche in Clausius, l’espressione "unico risultato" è fondamentale: ad esempio, nelle macchine frigorifere, si realizza il passaggio di calore da un corpo freddo ad uno caldo, a patto di compiere lavoro dall’esterno.

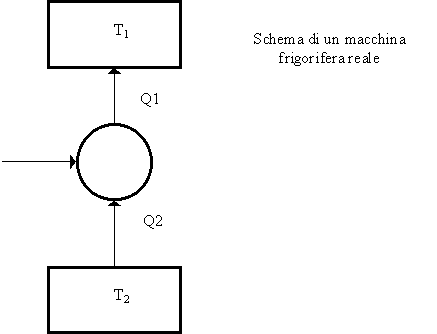
Fig. 7

Per dimostrare che le due formulazioni sono equivalenti, procediamo per assurdo.

1. Negazione dell’enunciato di Kelvin - Planck.

Supponiamo falso l’enunciato di Kelvin - Planck, ossia supponiamo di poter costruire una motore ideale che converta integralmente il calore in lavoro. Utilizziamo questo lavoro per far funzionare un frigorifero reale (Fig. 8). Esso assorbe il calore Q₂’ dal serbatoio a temperatura minore e cede il calore Q₁’ = Q₂’ + L al serbatoio a temperatura maggiore. Consideriamo ora la macchina termica complessiva, formata dal motore ideale e dal frigorifero reale. L viene prodotto e scambiato all’interno di questa macchina e non entra in relazione con l’esterno.

Quindi la macchina assorbe Q₂’ dal serbatoio a bassa temperatura e cede al serbatoio a temperatura maggiore il calore Q₁’ -Q₁. Ma poiché Q₁ = L (negazione di Kelvin -Planck), si ha:

Q₁’ - Q₁ = Q₁’ - L = Q₂’.

Ne deriva che è possibile trasferire, quale unico risultato del ciclo di trasformazione, Q₂’ dalla sorgente a temperatura inferiore a quella a temperatura superiore.

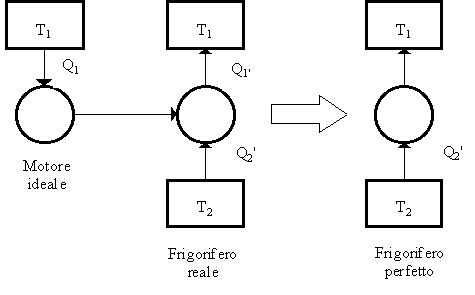
Fig. 8

2. Negazione dell’enunciato di Clausius.

Si può fare la stessa dimostrazione partendo dalla negazione dell’enunciato di Clausius: supponiamo che sia possibile trasferire calore da un corpo freddo ad un corpo caldo (Q₂). Come si vede dallo schema sotto, i Q₂ si elidono ed è possibile costruire un motore perfetto.

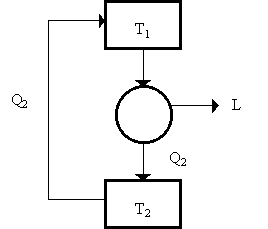
Fig. 9

PROCESSI REVERSIBILI E IRREVERSIBILI

Gli enunciati del secondo principio vietano qualcosa, ma non stabiliscono il limite

della conversione di calore in lavoro. Occorre passare da una formulazione qualitativa ad una formulazione quantitativa del secondo principio (come accadeva per il 1° principio), e per far questo abbiamo bisogno di una nuova grandezza fisica: l’entropia.

Distinguiamo due categorie di processi:

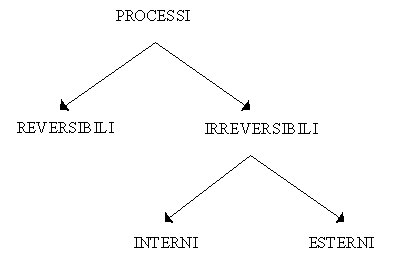
 Ora analizziamoli nel dettaglio:

• reversibili: processi per i quali è possibile riportare sia il sistema sia l’ambiente nella condizione iniziale, senza alcun effetto secondario. Bisogna prestare molta attenzione a questa definizione, perché spesso ci si dimentica dell’ambiente circostante e si pensa che la reversibilità sia collegata esclusivamente al sistema.
• irreversibili: processi non reversibili. Si distingue inoltre tra irreversibilità interna al sistema (ad es. gli attriti e tutti gli altri fenomeni dissipativi), ed irreversibilità esterna (flussi di calore tra il sistema e l’ambiente).

Facciamo alcuni esempi:

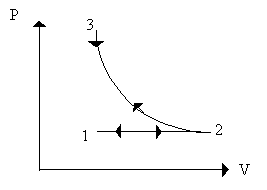
Fig. 10

Considero il sistema pompa della bicicletta con il foro aperto, senza attriti, schematizzato dal tratto 1-2 sul grafico (Fig. 10): esso è un processo reversibile.

Se ora chiudo il foro, ma faccio avvenire le trasformazioni molto lentamente lungo il percorso 2-3, il processo è ancora reversibile.

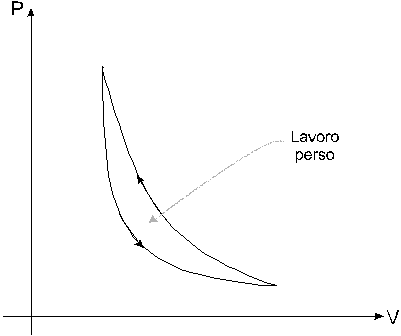
Fig. 11

Supponiamo ora di far avvenire il processo di pompaggio velocemente, per cui si hanno delle variazioni brusche e la curva di andata (adiabatica) è più ripida di quella di ritorno (Fig. 11). L’area tra le due curve rappresenta l’energia dissipata in calore. L’ambiente riceve calore e la persona che pompa la bicicletta dissipa energia, per cui è un processo irreversibile.

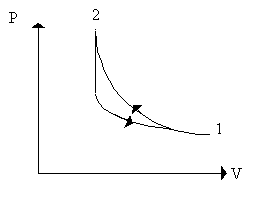
Fig. 12

In Fig. 12 la curva di andata indica un pompaggio molto veloce, al termine del quale avviene un raffreddamento, quindi si ritorna allo stato iniziale mediante un curva meno ripida. Anche questo è un processo irreversibile.

Limitandoci alle trasformazioni lente e mettendo i serbatoi a contatto col sistema ad una temperatura prossima a quella del sistema stesso (cosa di per sé irrealizzabile), si potrebbero eliminare le irreversibilità esterne.

Ciò non è possibile nella realtà: le trasformazioni reversibili non esistono. Quindi, nella migliore delle ipotesi, si può sperare che le irreversibilità interne scompaiano, mentre quelle esterne sono sempre presenti: in tal caso si parla di processo internamente invertibile. Tale processo è quasi statico: si conosce il suo grafico, cioè tutti gli stati intermedi.

Consideriamo un processo quasi statico, cioè internamente reversibile, che va da A a B in un diagramma (p,V). E’ sempre possibile costruire un cammino alternativo che collega i due punti, costituito da un tratto di adiabatica, un’isoterma e un secondo tratto di adiabatica. Si possono avere infinite isoterme che connettono i due tratti di adiabatica, ma noi scegliamo, tra tutti i cammini possibili, quello la cui area sottesa è identica all’area sottesa dal cammino di partenza.

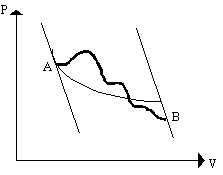
Fig. 13

Dal primo principio, si ha:

D U = Q - L

D U è uguale nei due casi, L è lo stesso (infatti si è scelto il tragitto con uguale area sottesa), dunque anche Q è lo stesso. Abbiamo tracciato un nuovo cammino che, a tutti gli effetti, è equivalente a quello iniziale.

Si prenda ora un trasformazione ciclica e si proceda come sopra, approssimandola con tanti trattini di adiabatica seguiti da isoterma.

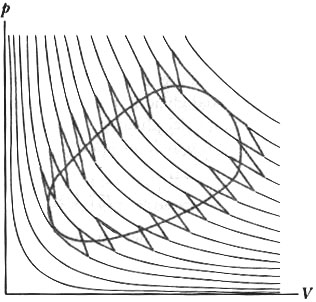
Fig. 14

Lungo le adiabatiche non si hanno scambi di calore, tutto il calore è scambiato lungo le isoterme. Quando il sistema scambia calore con le isoterme, possiamo pensare che sia collegato con un serbatoio alla sua stessa temperatura, in modo da eliminare le irreversibilità esterne.

Consideriamo il seguente integrale ciclico:

Se il sistema ha lavorato reversibilmente, l’integrale è nullo; se ci sono state irreversibilità esterne, l’integrale è minore di zero, e si ottiene la disuguaglianza di Clausius:

Se l’integrale risultasse maggiore di zero, violerebbe il secondo principio nell’enunciato di Clausius, ossia sarebbe possibile costruire una serie di macchine che operano irreversibilmente e portano al risultato di trasferire calore dal freddo al caldo.

La disuguaglianza di Clausius non dà effettivi vantaggi in termini quantitativi, perché l’integrale ciclico può essere molto difficile da valutare.

Per questo motivo, conviene introdurre una nuova grandezza fisica: l’entropia, il cui simbolo è S.

L’entropia è una funzione di stato, quindi non dipende dal cammino seguito ma solo dagli stati iniziale e finale e, come l’energia interna, è definita a meno di un valore assoluto (cioè è necessario stabilire una convenzione).

Per definizione:

L’integrale deve svolgersi lungo una trasformazione reversibile, altrimenti non è possibile calcolarlo perché non si conoscono gli stati intermedi. La (2) dice che qualunque sia il cammino reversibile scelto si ottiene lo stesso risultato. Sta alla nostra astuzia prendere un cammino che renda il calcolo facile.

In un diagramma (p,V), prendiamo due punti 1 e 2 e supponiamo di compiere una trasformazione reversibile e una irreversibile (che non può essere graficata, e in Fig. 15 è tratteggiata):

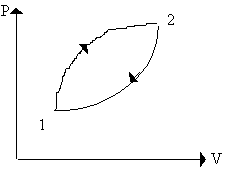
Fig. 15

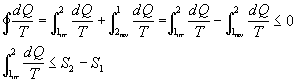
Si ha che l’integrale lungo il cammino irreversibile, ammesso che di riuscire a calcolarlo, è minore del salto di entropia. Ciò è anomalo dal momento che l’entropia è una funzione di stato e qualunque cammino si percorra dovremmo avere lo stesso risultato.

Si parla allora, anche se il termine è suscettibile di critiche, di produzione di entropia:

durante un processo irreversibile si produce entropia, mentre un processo reversibile la mantiene.

Valutando l’entropia dell’universo (sistema + ambiente):

• caso reversibile: D S_u = 0
• caso irreversibile: D S_{u >} 0

ß

(3) D S_{u ³} 0

Si può ora dare una formulazione del secondo principio nota come principio di non diminuzione dell’entropia : In qualsiasi trasformazione termodinamica che evolva tra due stati di equilibrio, l’entropia dell’insieme costituito dal sistema più l’ambiente circostante può solo restare costante o aumentare.

Ad esempio, possiamo pensare di far calare l’entropia del sistema, ma ciò implica necessariamente un aumento di entropia nell’ambiente che può essere uguale o maggiore dell’entropia persa dal sistema. L’importanza di questa formulazione del secondo principio sta nell’aver stabilito la cosiddetta "freccia del tempo" : non si può tornare indietro.