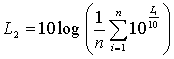Argomenti trattati:
-Isolamento acustico
-potere fonoisolante
-risonanze e coincidenze
-isolamento da calpestio
-Tecniche di previsione numerica
Isolamento acustico
In questa lezione verrà ripresa
e ampliata la teoria dell’isolamento acustico che è stata già introdotta nelle
lezioni precedenti.
La teoria dell’isolamento
acustico consiste nello studio del livello sonoro in un ambiente diverso da
quello in cui è posta la sorgente del suono. La superficie di separazione tra i
due ambienti è detta parete o solaio, a seconda che si tratti di
un divisorio verticale od orizzontale. Poniamoci ora per ipotesi nel caso di
figura 1:
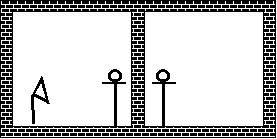
Figura 1
Due stanze sono separate
da una parete di cui ci interessa determinare le proprietà di isolamento; nella
stanza 1 è posta la sorgente del suono (ad esempio un altoparlante), mentre in
prossimità della parete sono posto due microfoni, che misurano l’intensità del
suono sulle due diverse facce della parete.
Le proprietà del
divisorio si descrivono mediante il coefficiente di trasmissione (t),
definito come rapporto tra l’intensità del suono trasmesso nella stanza 2 e
l’intensità del suono incidente sulla faccia rivolta nella stanza 1:
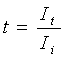 (1)
(1)
In
particolare si utilizza la grandezza detta potere fonoisolante (R):
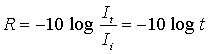 (2)
(2)
Il
potere fonoisolante è pertanto l’espressione logaritmica, in dB, dell’inverso
del coefficiente di trasmissione.
L’andamento di R è
funzione di diversi fattori: i principali sono la frequenza f dell’onda
e la densità superficiale s del divisorio, cioè la sua massa per unità di
superficie; la legge che governa questo andamento, almeno dal punto di vista
teorico, è la cosiddetta legge di massa. Essa è ottenuta risolvendo
l’equazione dell’onda nella doppia interfaccia aria-solido e solido-aria, e la
sua espressione, nel caso di un’onda incidente normalmente sulla parete, è la
seguente:
![]()
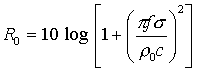 (3)
(3)
In
questa espressione il prodotto r0c è l’impedenza
caratteristica dell’aria (circa 410 kgm-2s-1); poiché
si ha che tipicamente (pfs/r0c)2>>1,
l’equazione (3) si può semplificare così:
![]() (4)
(4)
Da ciò si deduce che raddoppiando
la frequenza o la massa della parete, si ha di conseguenza un aumento di 6 dB
di R0, per le proprietà del logaritmo.
Nella pratica questa
espressione necessita di una leggera modifica. Infatti il suono non incide
generalmente in modo perpendicolare al divisorio, e nell’equazione (4) il
prodotto fs va moltiplicato per il coseno dell’angolo di
incidenza. Nel caso di un campo sonoro mediamente diffuso, come è tipicamente
il caso esaminato, nel quale l’incidenza è tendenzialmente casuale, si osserva
sperimentalmente che R risulta all’incirca 5-6 dB inferiore al valore
teorico di R0:
![]() (5)
(5)
Con un campo sonoro
perfettamente diffuso, la diminuzione di R sarebbe stata ancora
maggiore.

(a) (b)
Figura 2
Risonanze e coincidenze
La legge di massa
approssima bene l’andamento del potere fonoisolante in una regione di frequenze
intermedie. Alle basse ed alle alte frequenze compaiono fenomeni che fanno
discostare R da questa tendenza: sono rispettivamente le risonanze e
le coincidenze.
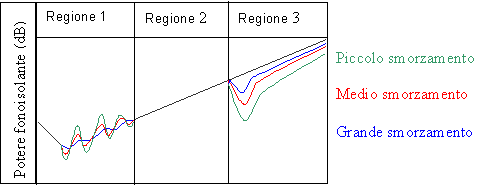
Figura 3
Le risonanze
avvengono alle basse frequenze, cioè nella regione 1 della figura 3; esse
corrispondono al modo tipico di vibrare di una lastra nel suo contorno. Il
fatto che una parete sia o no incernierata influisce sulle frequenze di
risonanza. Abbiamo parlato di frequenze, poiché la lastra è in grado di vibrare
in modi diversi; a ciascuno di essi corrisponderà una data frequenza.

Figura
4
La figura 4 esemplifica
un modo vibratorio; le regioni demarcate dai segni “+” e “-“ rappresentano le
zone di massimo e di minimo della vibrazione. In questo caso è stato
raffigurato il modo 2,1; esiste una formula che esprime le frequenze di
risonanza in funzione dei modi vibratori (m,n) e dello spessore (S), densità (r), dimensioni (A,B), modulo elastico (E) e modulo
di Poisson (n) del materiale:
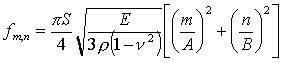
(6)
Al crescere dello
spessore crescono anche le frequenze di risonanza; le finestre hanno
solitamente basse frequenze, che tendono ad essere vibrazioni più che suoni. Al
contrario un muro, avente frequenze dell’ordine di 150-250 Hz, presenta
risonanze già in un regime acustico. Il tutto dipende naturalmente anche dalle
dimensioni della lastra.
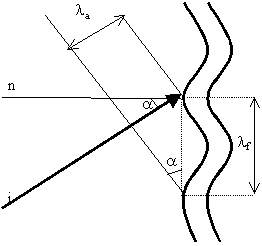
Figura 5
Le coincidenze
invece sono indipendenti dalla larghezza e dalla lunghezza: in questo caso è
determinante la lunghezza d’onda con cui flette la lastra quando vibra.
L’effetto di coincidenza ha luogo quando la lunghezza d’onda delle onde sonore la
coincide appunto con la proiezione della lunghezza d’onda flessionale del
divisorio lf lungo la direzione di
incidenza delle onde sonore; cioè, come si vede in figura 5, quando:
la = lf
sin a (7)
In questa condizione si
ha infatti coesione tra i punti di massimo e di minimo dell’onda incidente e
dell’onda flessionale, con un conseguente massimo trasferimento di energia. In
questo modo i fenomeni dissipativi vengono ridotti al minimo, e l’energia tende
a fluire attraverso la parete quasi come se non ci fosse; si ha dunque un
drastico abbassamento del potere fonoisolante. In generale esistono diverse
frequenze di coincidenza, superate le quali l’andamento del potere fonoisolante
non torna più al livello teorico dettato dalla legge di massa, ma resta
sensibilmente inferiore (circa 5-10 dB). La più bassa frequenza di coincidenza,
o frequenza critica fc, è quella relativa all’incidenza
radente (a=90°); il suo valore si può calcolare con la formula:
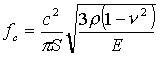 (8)
(8)
dove le grandezze sono le
stesse definite per l’equazione 6.
La frequenza fc
rappresenta il punto in cui la curva del potere fonoisolante comincia a
scendere; il valore minimo è quello relativo all’incidenza di 45°. Di
conseguenza fmax è ![]() volte la frequenza critica. I vetri in particolare
manifestano una forte caduta del potere fonoisolante quando si arriva a fmax.
Un espediente a questo problema può essere l’utilizzo dei doppi vetri: poiché
le due lastre hanno un diverso spessore, le due fmax sono
differenti. Pertanto una perdita di potere fonoisolante provocata da una
singola superficie viene compensata dall’altra.
volte la frequenza critica. I vetri in particolare
manifestano una forte caduta del potere fonoisolante quando si arriva a fmax.
Un espediente a questo problema può essere l’utilizzo dei doppi vetri: poiché
le due lastre hanno un diverso spessore, le due fmax sono
differenti. Pertanto una perdita di potere fonoisolante provocata da una
singola superficie viene compensata dall’altra.
Come si è visto, gli
scostamenti dalla legge di massa sono principalmente scostamenti negativi, cioè
tendono a rendere il potere fonoisolante inferiore al valore teorico possibile.
La legge di massa rappresenta dunque un valido riferimento dal punto di vista
della progettazione di strutture a maggior isolamento acustico. Tuttavia non è
sempre possibile, per esigenze costruttive, realizzare divisori ad alto peso
specifico; è dunque utile individuare strutture più complesse che abbiano
migliori capacità isolanti a parità di massa. Sul modello dei doppi vetri sono
costruite le cosiddette pareti doppie: anche in questo caso gli spessori
o ancor meglio i materiali delle due pareti non devono essere gli stessi, per
evitare la coincidenza delle frequenze di vibrazione, e non devono essere
rigidamente connessi (figura 6):
![]()
Figura 6
L’intercapedine tra i due
divisori è solitamente costituita da un isolante termico (come il polistirolo o
la lana di roccia). E’ un errore ritenere che questi materiali siano anche
ottimi isolanti acustici: il polistirolo e rigido oltre che essere leggero come
la lana di roccia. In generale le proprietà di isolamento acustico e termico
sono abbastanza discordanti: i migliori isolanti termici sono materiali porosi
e areati, in modo da garantire le proprietà isolanti dell’aria ferma; ma
materiali di questo tipo sono inevitabilmente leggeri e faticano a smorzare le
onde sonore. Un ottimo divisorio è quindi ottenuto dal giusto compromesso tra
le due capacità isolanti.
Spesso è necessario
riassumere le capacità di isolamento di un divisorio, che abbiamo visto
dipendere dalla frequenza, con un unico valore. Il potere fonoisolante viene
così sostituito da un numero, detto indice di valutazione del potere
fonoisolante (Rw). Le regole che definiscono il calcolo
dell’indice di valutazione sono contenute, secondo il decreto del 5-12-97,
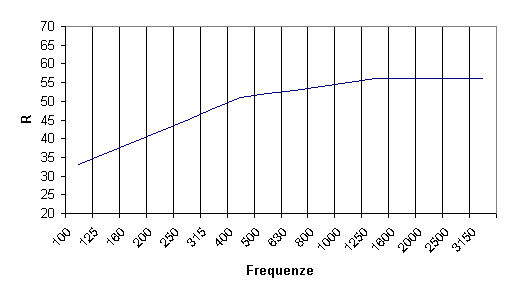
nella norma UNI 8270. Si utilizza la curva tipica normalizzata ISO 717-1:
R |
33 |
36 |
39 |
42 |
45 |
48 |
51 |
52 |
Frequenza |
100 |
125 |
160 |
200 |
250 |
315 |
400 |
500 |
R |
53 |
54 |
55 |
56 |
56 |
56 |
56 |
56 |
Frequenza |
630 |
800 |
1000 |
1250 |
1600 |
2000 |
2500 |
3150 |
La curva normalizzata presenta intervalli di frequenza in terzi
d’ottava compresi tra 100 e 3150 Hz. A frequenze basse ha una pendenza di 3 dB/ottava,
che scende a 1 dB/ottava alle medie frequenze e si assesta a un valore costante
per le alte. Questo andamento è utile per due motivi: innanzitutto approssima
l’isolamento tipico di una parete. Inoltre tiene anche conto della curva di
ponderazione A, per la quale conta di più avere isolamento a frequenze elevate.
Il suo uso è oggi consolidato, indipendentemente dalle sue origini.
Per ottenere l’indice di
valutazione Rw si raffrontano i dati sperimentali con la
curva normalizzata. Per far ciò, si sovrappone la curva al grafico sperimentale
e la si fa calare finchè la somma degli scostamenti positivi risulta minore di
32. Gli scostamenti positivi sono quelli per i quali il valore della curva
normale è maggiore del dato sperimentale: un eccessivo scostamento significa
infatti che l’isolamento è inferiore rispetto al livello normalizzato. Quando
si raggiunge il punto per il quale lo scostamento è inferiore a 32, allora si
considera il valore della curva normale corrispondente alla frequenza di 500
Hz: questo valore è Rw. In questo modo si ricava l’indice di
valutazione del potere fonoisolante nel caso di un divisorio verticale.
Il seguente foglio di
Excel calcola automaticamente la somma degli scostamenti positivi dalla curva
normalizzata in funzione della posizione della curva rispetto al grafico, cioè
in funzione appunto dell’indice di valutazione. Per ottenere il valore di Rw
corretto è sufficiente aumentare o diminuire quest’ultimo finchè la somma
degli scostamenti positivi risulta inferiore a 32. Nel caso della curva
sperimentale inserita come esempio l’indice di valutazione è pari a 45.
In questa tabella è
contenuto il valore indicativo del potere fonoisolante e l’indice di
valutazione di alcuni divisori di uso comune:
Tipo di divisorio |
R (in dB)
alle frequenze (Hz) |
Rw |
|||||
|
125 |
250 |
500 |
1000 |
2000 |
4000 |
||
|
Parete di mattoni piena intonacata (s=12 cm, p=220 kg/m2) |
34 |
35 |
40 |
50 |
55 |
57 |
45 |
|
Parete di mattoni piena intonacata (s=24 cm, p=440 kg/m2) |
40 |
44 |
50 |
56 |
57 |
57 |
54 |
|
Parete di mattoni forati (s=28 cm) |
37 |
43 |
52 |
60 |
64 |
65 |
57 |
|
Parete in calcestruzzo intonacata (s=18 cm, p=440 kg/m2) |
40 |
42 |
50 |
58 |
66 |
68 |
54 |
|
Parete in calcestruzzo (2 strati di 5 cm, separati da
intercapedine di 2,5 cm) |
37 |
40 |
44 |
50 |
56 |
62 |
49 |
|
Parete in calcestruzzo (2 strati di 7,5 cm, separati da
intercapedine di 7,5 cm) |
37 |
40 |
50 |
54 |
56 |
63 |
52 |
|
Divisorio in gesso-perlite (s=5 cm, p=49 kg/m2) |
26 |
28 |
30 |
31 |
42 |
47 |
33 |
|
Divisorio in gesso-perlite (s=6,3 cm, p=107 kg/m2) |
31 |
30 |
29 |
35 |
45 |
52 |
34 |
|
Tramezzo mobile |
15 |
22 |
26 |
27 |
33 |
35 |
29 |
|
Tramezzo mobile munito di pannelli vetrati (cristallo
7-9 mm di spessore) |
17 |
20 |
25 |
24 |
28 |
28 |
26 |
|
Tramezzo mobile munito di pannelli vetrati con doppio
cristallo (2 lastre uguali distanti 1 cm) |
17 |
20 |
23 |
33 |
33 |
33 |
25 |
|
Tramezzo mobile munito di pannelli vetrati con doppio
cristallo (2 lastre di diverso spessore distanti 4 cm) |
22 |
27 |
30 |
30 |
36 |
38 |
32 |
|
Idem con porta |
20 |
22 |
27 |
30 |
30 |
35 |
30 |
|
Doppia finestra |
16 |
24 |
36 |
50 |
54 |
58 |
36 |
Isolamento al calpestio
Ci proponiamo ora di
determinare le proprietà fonoisolanti di un divisorio orizzontale, o solaio.
In questo caso (figura 7) non interessa il rumore prodotto in aria nell’ambiente
superiore, ma il rumore generato dal calpestio sulla superficie divisoria;
nella stanza superiore non verrà posto dunque un altoparlante ma una macchina
apposita, detta macchina normalizzata di calpestio.
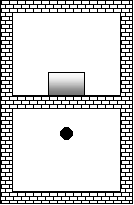
Figura 7
Le caratteristiche
tecniche della macchina, definite a norma di legge, fanno in modo che questa
produca un rumore standardizzato; il livello sonoro registrato dal microfono
della stanza inferiore viene detto livello normalizzato di calpestio (Ln,c).
Questo livello sonoro non dipende soltanto dalla natura del divisorio, ma
anche, in modo sensibile, dall’ambiente ricevente; in particolare influisce il
suo riverbero. Quindi si corregge il livello normalizzato di calpestio per il
tempo di riverberazione:
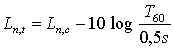 (9)
(9)
dove si è assunto come
tempo di riverbero tipico di una stanza arredata 0,5 secondi.
Anche per il livello
normalizzato di calpestio esiste un indice di valutazione, calcolato sulla
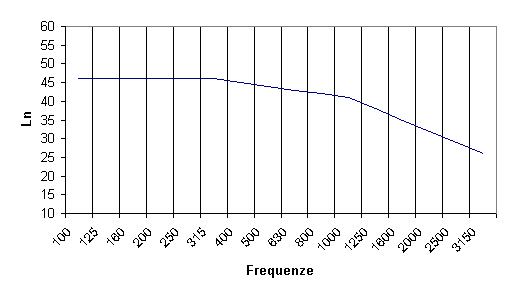
falsariga dell’indice di valutazione del potere fonoisolante. La curva
normalizzata (ISO 717-2) ha in questo caso un andamento speculare al
precedente:
Ln
|
46 |
46 |
46 |
46 |
46 |
46 |
45 |
44 |
Frequenza |
100 |
125 |
160 |
200 |
250 |
315 |
400 |
500 |
Ln
|
43 |
42 |
41 |
38 |
35 |
32 |
29 |
26 |
Frequenza |
630 |
800 |
1000 |
1250 |
1600 |
2000 |
2500 |
3150 |
Diversamente da prima la
curva va fatta ora salire sul grafico e non scendere: gli scostamenti positivi sono
quelli per i quali il livello di calpestio sperimentale è maggiore del livello
normalizzato. Infatti, mentre il potere fonoisolante era una caratteristica
positiva, il livello di calpestio deve essere il più basso possibile; cambiato
il segno agli scostamenti positivi, si ha che anche in questo caso la loro
somma deve essere minore di 32. Analogamente l’indice di valutazione del
livello di calpestio normalizzato, Ln,w, è il livello della
curva normale alla frequenza di 500 Hz quando è soddisfatta quella condizione.
Questo foglio di Excel è l’equivalente del precedente per il calcolo di Ln,w,:
E’ interessante notare
alcuni particolari della macchina normalizzata di calpestio (figura 8):
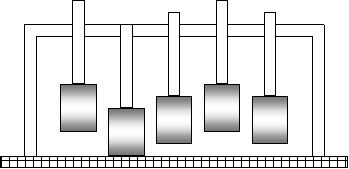
Figura 8
![]() (11)
(11)
Per il calcolo
dell’indice di valutazione si procede come nel caso del potere fonoisolante.
A questo punto, definite
le grandezze interessate dalla normativa del 5/12/1997, si può dare uno sguardo
ai valori limite imposti dal decreto. Innanzitutto bisogna notare come le varie
tipologie edilizie siano state suddivise in 7 categorie a seconda delle diverse
funzionalità:
|
categoria A: edifici adibiti a residenza o
assimilabili; |
|
categoria B: edifici adibiti ad uffici e
assimilabili; |
|
categoria C: edifici adibiti ad alberghi,
pensioni ed attività assimilabili; |
|
categoria D: edifici adibiti ad ospedali,
cliniche, case di cura e assimilabili; |
|
categoria E: edifici adibiti ad attività
scolastiche a tutti i livelli e assimilabili; |
|
categoria F: edifici adibiti ad attività
ricreative o di culto o assimilabili; |
|
categoria G: edifici adibiti ad attività
commerciali o assimilabili |
.
Questi sono i valori limite (limiti inferiori per Rw
e D2m,nT,w, superiore per Ln,w):
Categorie |
Parametri |
||
|
Rw |
D2m,nT,w |
Ln,w |
|
|
1) D |
55 |
45 |
58 |
|
2) A, C |
50 |
40 |
63 |
|
3) E |
50 |
48 |
58 |
|
4) B, F, G |
50 |
42 |
55 |
Bisogna
infine considerare che i limiti imposti a Rw sono sempre
riferiti a diverse unità immobiliari: la legge italiana non prevede infatti
limiti alle proprietà isolanti tra i divisori di uno stesso appartamento.
Tecniche di previsione numerica
Abbiamo visto finora come
sia possibile misurare le caratteristiche acustiche di un ambiente in modo
sperimentale; tuttavia riveste grande importanza anche il procedimento inverso,
cioè riuscire a prevedere queste caratteristiche, in particolare il livello
sonoro e il tempo di riverbero, data una particolare conformazione spaziale. Le
motivazioni possono essere diverse: ad esempio la progettazione di edifici dai
requisiti acustici particolari, come teatri o sale da concerto, o anche la
previsione di interventi su strutture già esistenti. I più interessanti modelli
numerici che implementano la propagazione del suono in spazi chiusi sono stati
sviluppati negli ultimi anni, a causa delle elevate capacità di calcolo
richieste dai modelli stessi.
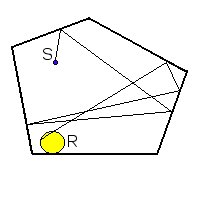
Uno dei primi modelli
utilizzati è il cosiddetto metodo delle sorgenti immagine: la
riflessione del suono lungo una superficie viene considerata speculare, e oltre
alla normale sorgente del suono se ne considera una virtuale posta
specularmente alla superficie (figura 9):
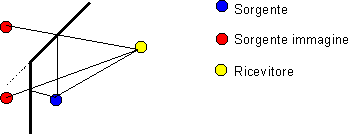
Figura 9
Per ogni superficie va considerata una nuova sorgente immagine;
inoltre le sorgenti immagine creano a loro volta sorgenti immagini di ordini
superiori. Se la struttura presenta una certa complessità geometrica, arrivare
a considerare sorgenti immagini di un certo ordine fa crescere la complessità
del calcolo in modo esponenziale. Un altro problema di questo modello è che non
tiene conto delle superfici assorbenti; è come se le superfici fossero tutte
speculari.
Un metodo diverso, più
recente e più preciso, è il raytracing; viene utilizzato anche nelle
simulazioni ottiche, anche se è nato inizialmente per l’acustica. Il metodo
consiste nel simulare una sorgente puntiforme che emette raggi in ogni
direzione; essi rimbalzano sulle superfici perdendo parte della loro energia.
Una parte dei raggi giungeranno a colpire un ricevitore non puntiforme (figura
10):
Figura 10
Il ricevitore è sferico poiché se fosse puntiforme la
probabilità che venga colpito è nulla. Quando viene colpito da un raggio,
quest’ultimo può avere incidenza maggiore o minore a seconda di diversi
fattori: lo spazio percorso, il numero di riflessioni subite, il modo in cui
colpisce il ricevitore. Per questo interessa calcolare la densità di energia
(W’) che trasmette ogni singolo raggio:
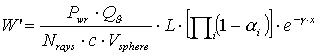 (12)
(12)
Il primo fattore
rappresenta l’energia iniziale posseduta dal raggio; L è lo spazio
percorso all’interno del ricevitore; la produttoria rappresenta l’assorbimento
da parte delle superfici di riflessione, aventi coefficienti di assorbimento ai; l’ultimo fattore è infine l’attenuazione causata dall’aria (coefficiente g e spazio percorso x), che influisce a
distanze e frequenze elevate. Il raytracing è anche detto metodo di
Montecarlo per la casualità nella generazione dei raggi, anche se la
generazione di raggi in modo perfettamente casuale attraverso una superficie
sferica presenta qualche difficoltà. Questo metodo è molto efficace e accurato
se viene generato un numero appropriato di raggi, perché è bassa la probabilità
di colpire il ricevitore.
Esiste un altro gruppo di
tecniche di previsione, quello dei tracciatori di fasci divergenti.
L’idea di base è simile a quella del raytracing; tuttavia in questo caso la
sorgente non emette raggi singoli, ma un fascio di raggi. Questo permette di
avere un ricevitore puntiforme, mantenendo al tempo stesso un numero
relativamente basso di fasci emessi. Esistono due metodologie di questo tipo: i
tracciatori a fasci conici e i tracciatori a fasci piramidali (pyramid
tracing).
I fasci conici presentano
il problema della sovrapposizione dei coni: è impossibile coprire una
superficie sferica senza lasciare delle lacune o senza coprire due volte uno
stesso settore (figura 11):
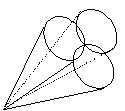
Figura 11
Per ovviare a questo
problema certi metodi mediano l’energia dei coni tramite una curva gaussiana,
in modo da attenuare la sovrapposizione dei bordi.
Nel pyramid tracing il fascio è a base triangolare (figura 12). La suddivisione di una sfera in triangoli non comporta particolari problemi: è possibile dividere la sfera in modo che la base delle piramidi abbia approssimativamente la stessa superficie. L’asse della piramide viene tracciato come nel raytracing; gli altri tre raggi, gli spigoli della piramide, vengono riflessi dalla stessa superficie dell’asse. Quando il ricevitore, puntiforme, si trova all’interno della piramide, subisce un contributo di energia.
Un limite del pyramid
tracing è il fatto che il fascio subisce sempre la riflessione rispetto alla
superficie sulla quale viene riflesso il raggio centrale. Poiché il fascio
diviene progressivamente sempre più ampio, potrebbe diventare più largo della
superficie di riflessione: in questo caso viene sottostimata la parte finale
della coda di riverbero, stima che viene corretta con opportuni algoritmi. Il
pyramid tracing ha il suo punto di forza nella velocità di calcolo (non è
necessario un numero elevato di fasci per ottenere una buona approssimazione).
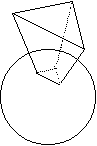
Figura 12
La precisione fornita dai
programmi si attesta generalmente attorno ad un errore di circa 5 dB,
riducibili a 2 dB in condizioni ottimali. Grazie al calcolo dell’ecogramma è
possibile ricostruire la risposta all’impulso (l’ecogramma è infatti una
risposta all’impulso teorica, priva della fase). Utilizzandola con filtri
convolutivi, si può simulare il suono come se fosse nell’ambiente studiato.
Questo procedimento prende il nome di auralizzazione, ed è
l’equivalente, in campo sonoro, della visualizzazione.